Ekkart Kindler a s d r a Tow

Ekkart Kindler … a s d r a Tow A framework for the definition of variants of high-level Petri nets Ekkart Kindler DTU Informatics, Technical University of Denmark Laure Petrucci LIPN, Université Paris 13

Situation Ekkart Kindler § Many different versions of high-level nets § Conceptually, many differences in the data types only § Technically, the differences are more scattered è Definitions structurally different è Difficult to compare different versions è Difficult to define (and understand) new versions A framework for the definition of variants of high-level Petri nets 2

Quest Ekkart Kindler Generic definition of high-level nets that allows for the definition of variants A framework for the definition of variants of high-level Petri nets 3

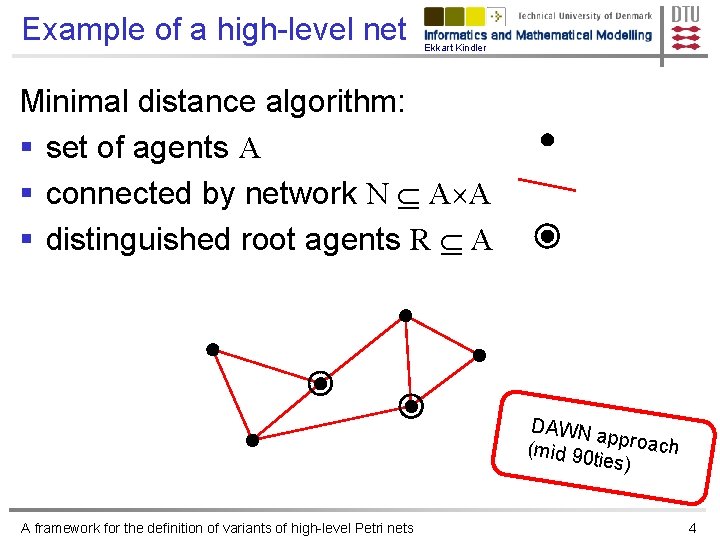
Example of a high-level net Ekkart Kindler Minimal distance algorithm: § set of agents A § connected by network N A A § distinguished root agents R A DAWN ap (mid 90 proach ties) A framework for the definition of variants of high-level Petri nets 4

Example: Net Scheme rootagents: AGENT R [x] messages: AGENT x nat [ (x, d) ] I inneragents: AGENT [x] Ekkart Kindler [ (x, 0) ] M(x, 1) [ (x, d) ] [ (x, n) ] d<n M(x, d+1) [ (x, d) ] distances: AGENT x nat [ (x, d) ] x: AGENT d: nat n: nat A framework for the definition of variants of high-level Petri nets 5

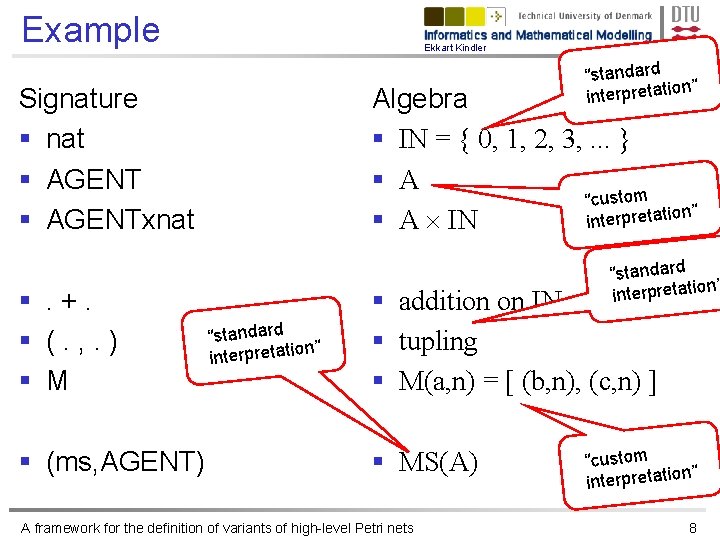
Example: Algebra Ekkart Kindler Signature § nat § AGENTxnat Algebra § IN = { 0, 1, 2, 3, . . . } § A IN §. +. § (. , . ) § M § addition on IN § tupling § M(a, n) = [ (b, n), (c, n) ] a § (ms, AGENT) c b § MS(A) A framework for the definition of variants of high-level Petri nets 6

Example rootagents: AGENT R “standard operations” [x] [ (x, 0) ] M(x, 1) [ (x, d) ] messages: AGENT x nat [ (x, n) ] “standard on constructs rts” arbitrary so d<n M(x, d+1) [ (x, d) ] I Ekkart Kindler [x] [ (x, d) ] inneragents: AGENT ators” er “custom op x: AGENT d: nat n: nat A framework for the definition of variants of high-level Petri nets distances: AGENT x nat rts” “custom so orts” “standard s 7

Example Ekkart Kindler “standard n” interpretatio Signature § nat § AGENTxnat §. +. § (. , . ) § M § (ms, AGENT) Algebra § IN = { 0, 1, 2, 3, . . . } § A “custom n” interpretatio § A IN “standard n” interpretatio § addition on IN § tupling § M(a, n) = [ (b, n), (c, n) ] § MS(A) A framework for the definition of variants of high-level Petri nets “custom n” interpretatio 8

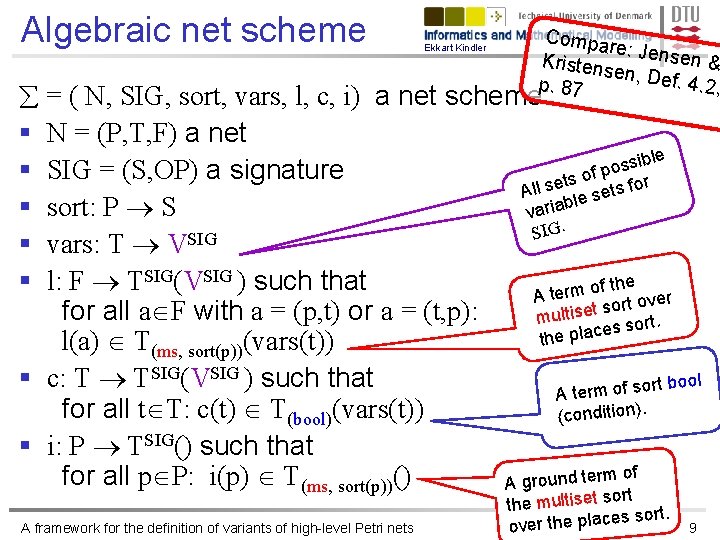
Algebraic net scheme Ekkart Kindler Compa re: Kristens Jensen & en, Def. 4. 2, p. 87 = ( N, SIG, sort, vars, l, c, i) a net scheme: § N = (P, T, F) a net ible s s o § SIG = (S, OP) a signature of p or s t e s sf t All e s ble § sort: P S varia SIG § vars: T V § l: F TSIG(VSIG ) such that of the A term ver o t r o s t for all a F with a = (p, t) or a = (t, p): multise ort. s s e c a l the p l(a) T(ms, sort(p))(vars(t)) § c: T TSIG(VSIG ) such that ort bool s f o m r e t A for all t T: c(t) T(bool)(vars(t)) (condition). § i: P TSIG() such that of for all p P: i(p) T(ms, sort(p))() A ground term A framework for the definition of variants of high-level Petri nets ort the multiset s s sort. e c la p e th r e v o 9

Algebraic net Ekkart Kindler A net scheme = ( N, SIG, sort, vars, l, c, i) together with a SIG-Algebra A is a algebraic net. + some restrictions on A A framework for the definition of variants of high-level Petri nets 10

Questions (1) Ekkart Kindler § Which “standard sorts”, “standard constructs” on sorts, “and “standard operations” are hich w , r a l u there? In partic nstructs o ultiset c m in the d e § What do they mean? s u may be arc labe ls? § What are the possible legal interpretations for the “custom sorts” and “custom operators” (if they are possible at all)? Answer these questions, and you have defined a new version of high-level nets A framework for the definition of variants of high-level Petri nets 11

Question (2) Ekkart Kindler § Technically, all standard sorts, operations and their interpretations need to be explicitly included into every algebraic net! that? Effort without any benefit! d i o v a n’t we Ca § Even worse: we must make sure that this is done in the right way (bool are the Booleans, nat are the naturals, ms are multisets, . . . ) Effort without any benefit! A framework for the definition of variants of high-level Petri nets 12

Idea: Generators Ekkart Kindler § Give a signature and algebra for the custom parts only! § ”Generate” all the standard stuff on top of this Generator dard n a t s e h s all t e eir n i h f t e h d t i r w o ng rat A gene operations, alo d sorts an ion. at t e r p r e dard t n in a t s e h hat t w s e n i f or de t a r e n e This g are. s t c u r t s con A framework for the definition of variants of high-level Petri nets 13

Generator Ekkart Kindler A generator is a pair of mapping (GS, GA): § GS maps a signature to a signature such that GS(SIG) SIG § GA maps an algebra to an algebra such that for every SIG-algebra A GA(A ) is a GS(SIG)-algebra with GA(A ) A A framework for the definition of variants of high-level Petri nets 14

Generator: Examples Ekkart Kindler TRUE adds the booleans but only with the constant true (no other operators). BOOL adds the booleans with their standard operators DOT adds the sort dot which represents the set { ● } PROD adds all products over all existing sorts (non recursively) MULT adds all multisets over all existing sorts (non recursively) A framework for the definition of variants of high-level Petri nets 15

Generator constructions Ekkart Kindler § Union of generators e. g. BOOL DOT § Sequential application ○ e. g. PROD ○ (BOOL DOT) § Recursive application * e. g. PROD* ○ (BOOL DOT) A framework for the definition of variants of high-level Petri nets 16

Combining generators GBT = (PROD)* ○ BOOL GMT = MULT Ekkart Kindler ebra g l A s ’ g i Reis 91 Nets 19 ic GBT = (MULT PROD)* ○ BOOL with s t e n c i ts Algebra h g i e w c ar GMT = ID flexible 8 9 1996/19 GBT = DOT TRUE GMT = MULT A framework for the definition of variants of high-level Petri nets n of o i t c i r t s re P/T-net ets n c i a r b alge 17

Net scheme of kind (GBT, GMT) Ekkart Kindler = ( N, SIG, sort, vars, l, c, i) a net scheme: ith w e § N = (P, T, F) a net r u t a Sign s and t r o s l a addition (in part. § SIG a signature rs with e operato r u t s) igna rts and t GBT(SIG) e S s i t l u m § sort: P S so basic ons ti opera § vars: T VGBT(SIG) § l: F TGMT(GBT(SIG))(VGBT(SIG) ) such that for all a F with a = (p, t) or a = (t, p): l(a) T(ms, sort(p))(vars(t)) § c: T TGMT(GBT(SIG))(VGBT(SIG) ) such that for all t T c(t) T(bool)(vars(t)) § i: P TGMT(GBT(SIG))() such that for all p P i(p) T(ms, sort(p))() A framework for the definition of variants of high-level Petri nets 18

Net scheme of kind (GBT, GMT) Ekkart Kindler = ( N, SIG, sort, vars, l, c, i) a net scheme: ith w e § N = (P, T, F) a net r u t a Sign s and t r o s l a addition (in part. § SIG a signature rs with e operato r u t s) igna rts and t GBT(SIG) e S s i t l u m § sort: P S so basic ons ti opera § vars: T VGBT(SIG) § l: F TGMT(GBT(SIG))(VGBT(SIG) ) such that for all a F with a = (p, t) or a = (t, p): l(a) T(ms, sort(p))(vars(t)) § c: T TGMT(GBT(SIG))(VGBT(SIG) ) such that for all t T c(t) T(bool)(vars(t)) § i: P TGMT(GBT(SIG))() such that for all p P i(p) T(ms, sort(p))() A framework for the definition of variants of high-level Petri nets 19

Questions (1) Ekkart Kindler § Which “standard sorts”, “standard constructs” on sorts, “and “standard operations” are there? § What do they mean? § What are the possible legal interpretations for the “custom sorts” and “custom operators” (if they are possible at all)? A framework for the definition of variants of high-level Petri nets 20

Construct: Examples Ekkart Kindler fixed t n i o j s i d Linearly ordered set: LO = (LOSIG, { (bool) }, {o, lt} , Ao) with LOSIG = ( { o, (bool) }, { lt: o o (bool) } ) and for every algebra A in Ao we have § A(o) is a finite set and § A(lt) is linear order over A(o) fixed t n i o j s i d Equality: EQ = (EQSIG, { (bool) }, { } , Ae) with EQSIG = ( { e, (bool) }, { eq: o o (bool) } ) and for every algebra A in Ae we have § A(eq) is a equality on A(e) A framework for the definition of variants of high-level Petri nets 21

Construct Ekkart Kindler A construct CON = (SIG, F, D, A) is a signature SIG, two subset of F and D symbols of SIG, and a class of SIG-algebras A. § F symbols with a fixed interpretation (via some generator, e. g. (bool), (ms, s), …) § D disjoint symbols (may not overlap with other constructs) § A legal interpretations A framework for the definition of variants of high-level Petri nets 22

Construct mapping Ekkart Kindler In a legal algebra A with respect to a set of constructs C, all parts must be constructed from constructs C only. we ; l a c i n h it tec b a s i n e! Definitio into details her o do not g A framework for the definition of variants of high-level Petri nets 23

Algebraic net Ekkart Kindler An algebraic net scheme = ( N, SIG, sort, vars, l, c, i) of kind (GBT, GMT) together with a SIG-algebra A that is constructed from constructs C only is an algebraic net of kind K = (GBT, GMT, C). A framework for the definition of variants of high-level Petri nets 24

Kinds of nets Ekkart Kindler GBT = (PROD)* ○ BOOL GMT = MULT CGBT raic b e g l A Reisig’s 91 Nets 19 well( s t e n tric Symme ts) 1991 ne formed C = { LO, EQ, UO, CS, PAR } GBT = (MULT PROD)* ○ BOOL with s t e n c i ts Algebra h g i e w c ar GMT = ID flexible CGBT = DOT TRUE GMT = MULT C={} A framework for the definition of variants of high-level Petri nets 8 9 1996/19 n of o i t c i r t s re P/T-net ets n c i a r b alge 25

Conclusion Ekkart Kindler § Details of the mathematics “behind the scenes”: see paper § With the predefined generators and constructs, it is easy to define new kinds of high-level Petri nets § without changing the definition of high-level ured o l o Petri nets C e to defin How ts? Petri Ne A framework for the definition of variants of high-level Petri nets 26