Bla Bollobs Guy Kindler Imre Leader Ryan ODonnell

Béla Bollobás Guy Kindler Imre Leader Ryan O’Donnell Memphis Microsoft Cambridge Microsoft
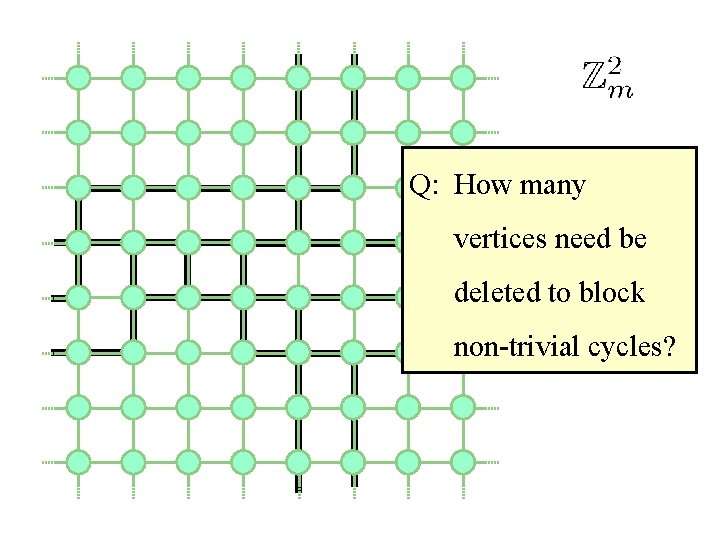
Q: How many vertices need be deleted to block non-trivial cycles?
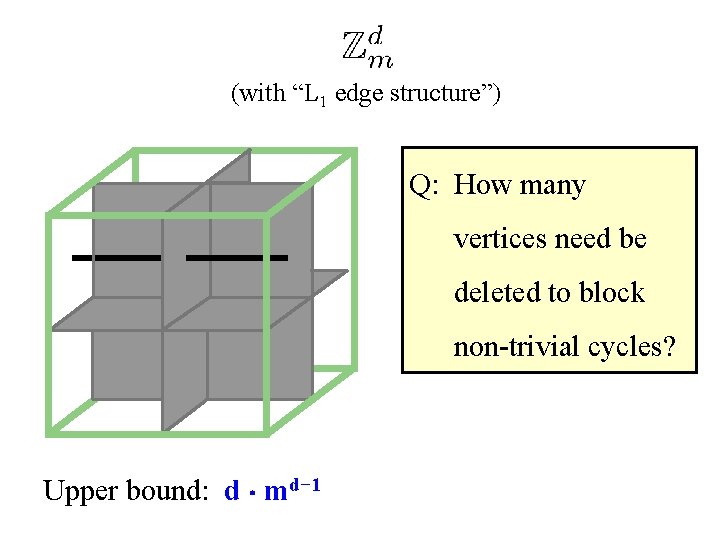
(with “L 1 edge structure”) Q: How many vertices need be deleted to block non-trivial cycles? Upper bound: d ¢ md− 1
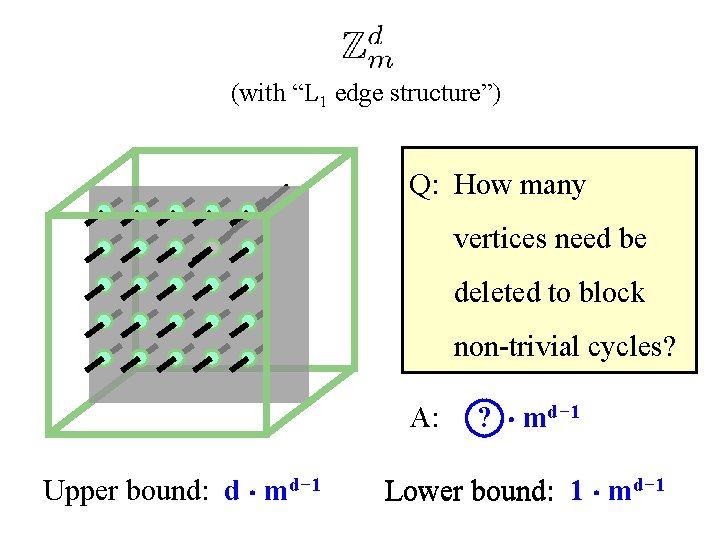
(with “L 1 edge structure”) Q: How many vertices need be deleted to block non-trivial cycles? A: Upper bound: d ¢ md− 1 ? ¢ md− 1 Lower bound: 1 ¢ md− 1
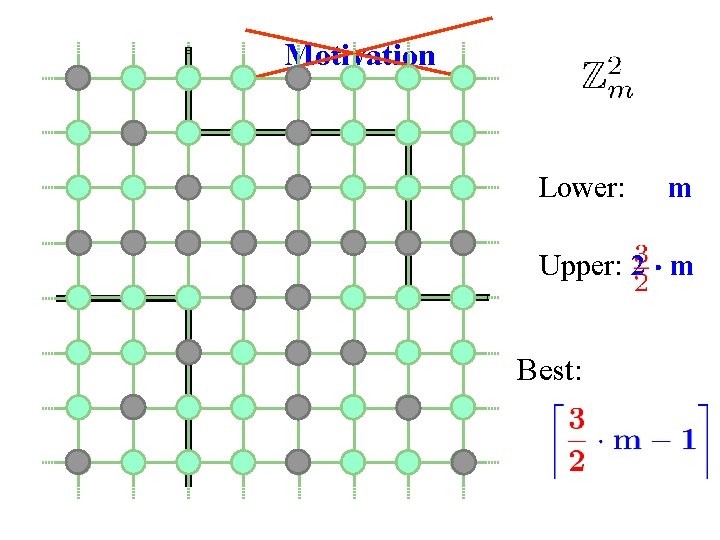
Motivation Lower: m Upper: 2 ¢ m Best:
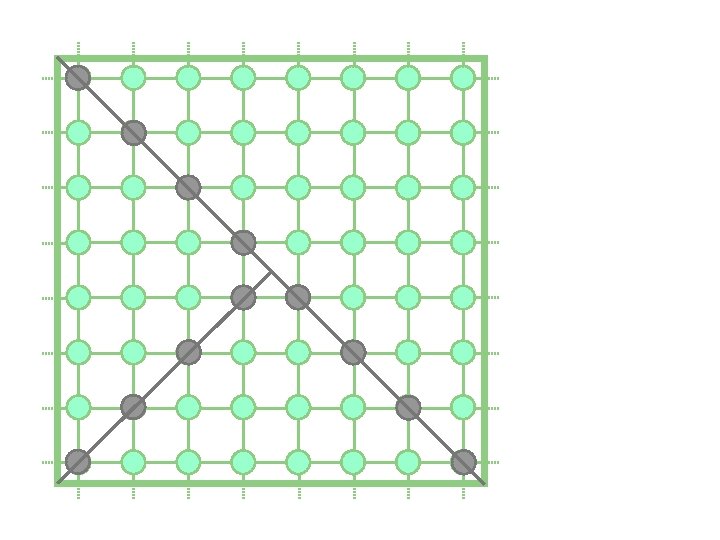
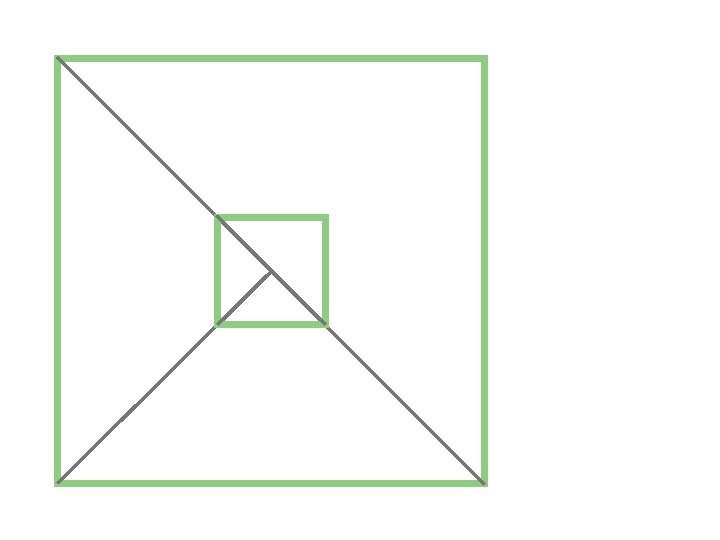
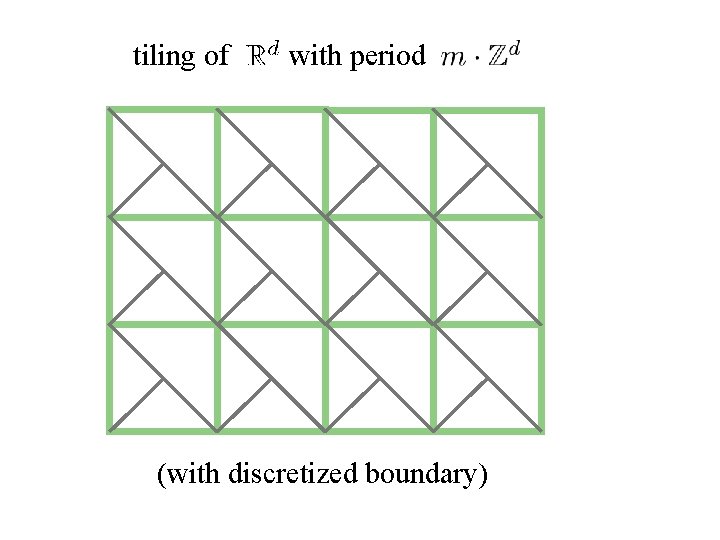
tiling of with period (with discretized boundary)
tiling of with period (with discretized boundary)
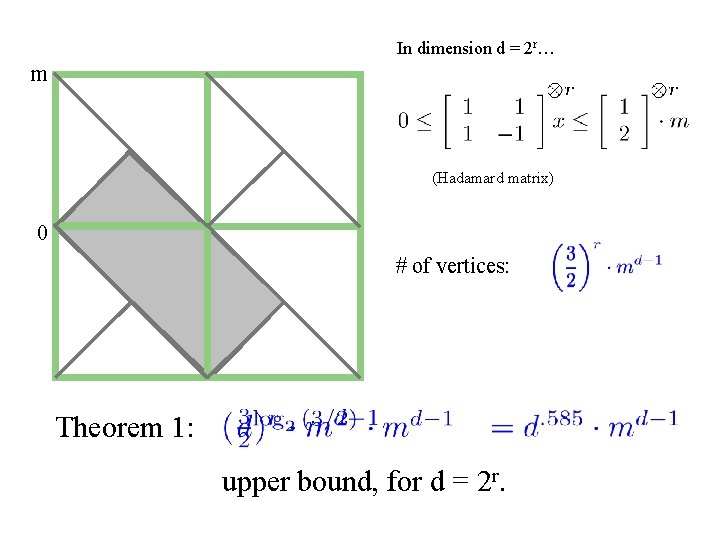
In dimension d = 2 r… m (Hadamard matrix) 0 # of vertices: Theorem 1: upper bound, for d = 2 r.
![Motivation • “L 1 structure”: • [SSZ 04]: Asymptotically tight lower bound. (Yields integrality Motivation • “L 1 structure”: • [SSZ 04]: Asymptotically tight lower bound. (Yields integrality](http://slidetodoc.com/presentation_image_h2/ebfb8c4e6335dce02a2453d483ecb05a/image-11.jpg)
Motivation • “L 1 structure”: • [SSZ 04]: Asymptotically tight lower bound. (Yields integrality gap for DIRECTED MIN MULTICUT. ) • Our Theorem 2: Exactly tight lower bound. • Edge-deletion version: Our original motivation. Connected to quantitative aspects of Raz’s Parallel Repetition Theorem.
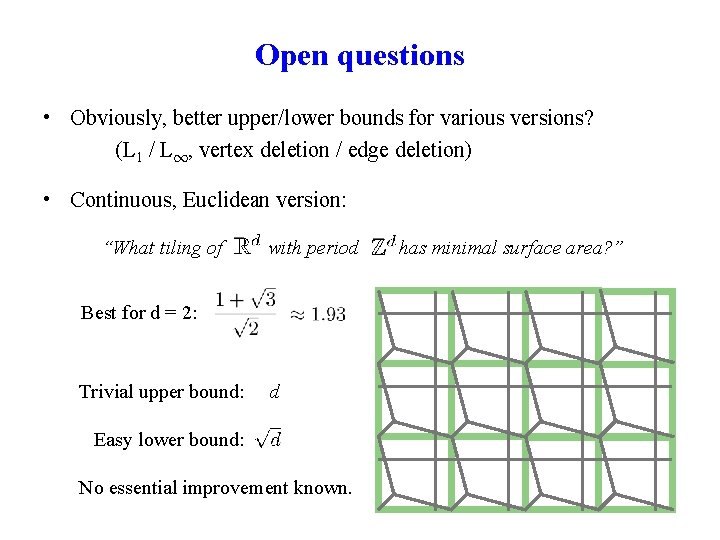
Open questions • Obviously, better upper/lower bounds for various versions? (L 1 / L 1, vertex deletion / edge deletion) • Continuous, Euclidean version: “What tiling of with period Best for d = 2: Trivial upper bound: d Easy lower bound: No essential improvement known. has minimal surface area? ”

- Slides: 13