CodeTesting Hastad Trevisan Samorodnitsky Widgerson Speaker Guy Kindler

Code-Testing Hastad, Trevisan, Samorodnitsky, Widgerson Speaker : Guy Kindler

Property Testing § Given: Input § Access: A few random bits § If: – Input has property: Accept – Input is FAR from property: Reject

Code Testing § Given: Input § Access: A few random bits § If: – Input if a code-word: Accept – Input is FAR from all code-words: Reject

Code Testing § Given: Input § Access: A few random bits § If: – Input if a code-word: Accept – Input is FAR from all code-words: Reject § Correlation between words: fraction( agreement ) – fraction( disagreement )

Hadamard (Linear) Code § An Entry A(x) for every x in (Z 2)n. § Codeword: A linear function § That is A: (Z 2)n Z 2 A(x)=a 1 x 1+a 2 x 2+. . +anxn where ai is 0 or 1

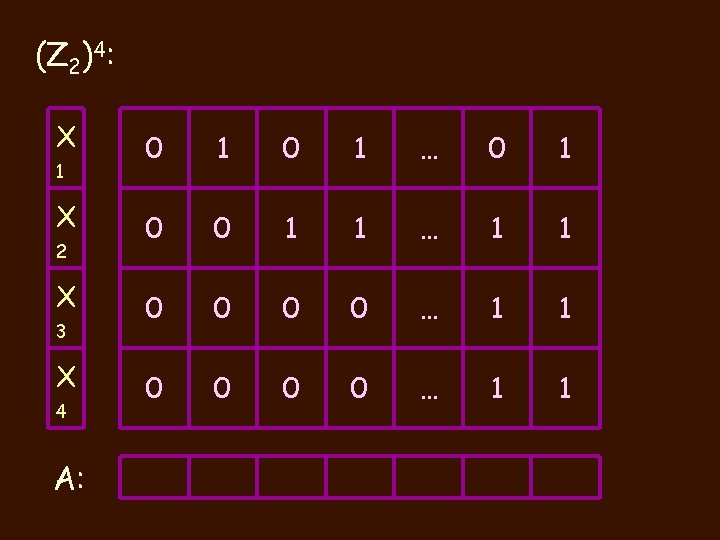
(Z 2)4: X 1 X 2 X 3 X 4 A: 0 1 … 0 1 0 0 1 1 … 1 1 0 0 0 0 … 1 1

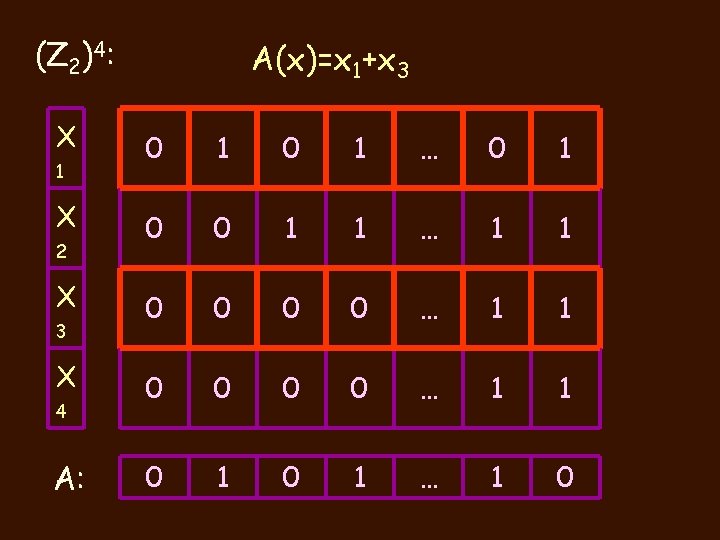
(Z 2)4: X 1 X 2 X 3 X 4 A: A(x)=x 1+x 3 0 1 … 0 1 0 0 1 1 … 1 1 0 0 0 0 … 1 1 0 1 … 1 0

Linear Test § Pick random x, y in (Z 2)4. § Verify that A(x)+A(y)=A(x+y) A: 0 1 … 1 0

Long Code § An Entry A(x) for every x in (Z 2)n. § Codeword: A linear function A: (Z 2)n Z 2 which depends on ONE coordinate § That is A(x)=xi

(Z 2)4: X 0 1 … 0 1 1 0 0 1 1 … 1 1 2 0 0 0 0 … 1 1 X X 3 X A: 4

X 0 1 … 0 1 1 0 0 1 1 … 1 1 2 0 0 0 0 … 1 1 0 0 1 1 … 1 1 x y x+y X X 3 X A: 4

Pick x, y and noise z: zi=1 with probability X 0 1 … 0 1 1 0 0 1 1 … 1 1 2 0 0 0 0 … 1 1 0 0 1 1 … 1 1 x y x+y X X 3 X A: 4 x+y+z

Pick x, y and noise z: zi=1 with probability X 0 1 … 0 1 1 0 0 1 1 … 1 1 2 0 0 0 0 … 1 1 0 0 1 1 … 1 1 x y x+y X X 3 X A: 4 x+y+z Test: Verify A(x)+A(y)=A(x+y+z)

Itterated Test § Pick x 1, . . , xk. § For all i<j, verify A(xi)+A(xj)=A(xi+xj)

Change of Notation 0 ------> 1 1 ------> -1 + ------> multiplication

X 1 -1 … 1 -1 -1 … -1 -1 2 1 1 1 1 … -1 -1 X X 3 X A: 4

X 1 -1 … 1 -1 -1 … -1 -1 2 1 1 1 1 … -1 -1 1 1 -1 X X 3 X A: 4

X 1 -1 … 1 -1 -1 … -1 -1 2 1 1 1 1 … -1 -1 1 1 -1 X X 3 X A: 4 Correct Code-word:

Properties of Code-words § Expected value of a code-word is zero (!). § If A and B are code-words, so is AB:

Inner Product § Let A, B be functions over {1, -1}n <A, B> : = Ex[ A(x)B(x) ] § Code-Words: an orthnormal basis!

Inner Product § Let A, B be functions over {1, -1}n <A, B> : = Ex[ A(x)B(x) ] § Code-Words: an orthnormal basis! § Conclusion: ANY A: {1, -1}n {-1, 1} is of the form

Fourier Expansion

Linear Test § Pick x, y § Verify that A(x)A(y)=A(xy(

Long-code Test § Pick random x, y § Pick z such that zi=-1 with prob . § Verify that A(x)A(y)=A(xy)

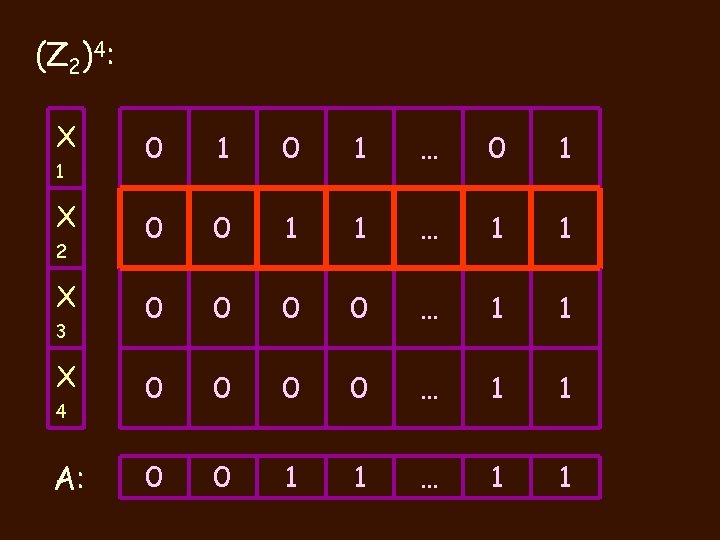
(Z 2)4: X 1 X 2 X 3 X 4 A: 0 1 … 0 1 0 0 1 1 … 1 1 0 0 0 0 … 1 1 0 0 1 1 … 1 1