E D O de segundo orden no homognea

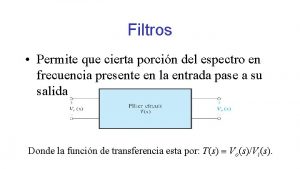
E. D. O. de segundo orden no homogénea con coeficientes constantes Cuando

Dependencia e independencia lineal Un conjunto de funciones f 1(x), f 2(x), …, fn(x) es linealmente dependiente en un intervalo I, si existen ciertas constantes c 1, c 2, …, cn no todas nulas, tales que: c 1 f 1(x) + c 2 f 2(x) + … + cn fn(x) = 0 Si el conjunto no es linealmente dependiente, entonces es linealmente independiente. En otras palabras, si el conjunto es linealmente independiente, cuando: c 1 f 1(x) + c 2 f 2(x) + … + cn fn(x) = 0 entonces necesariamente c 1 = c 2 = … = cn = 0. 2

Ejemplo: Las funciones f 1 = cos 2 x, f 2 = sin 2 x, f 3 = sec 2 x, f 4 = tan 2 x son linealmente dependientes en el intervalo (- /2, /2) porque c 1 cos 2 x +c 2 sin 2 x +c 3 sec 2 x +c 4 tan 2 x = 0 con c 1 = c 2 = 1, c 3 = -1, c 4 = 1.

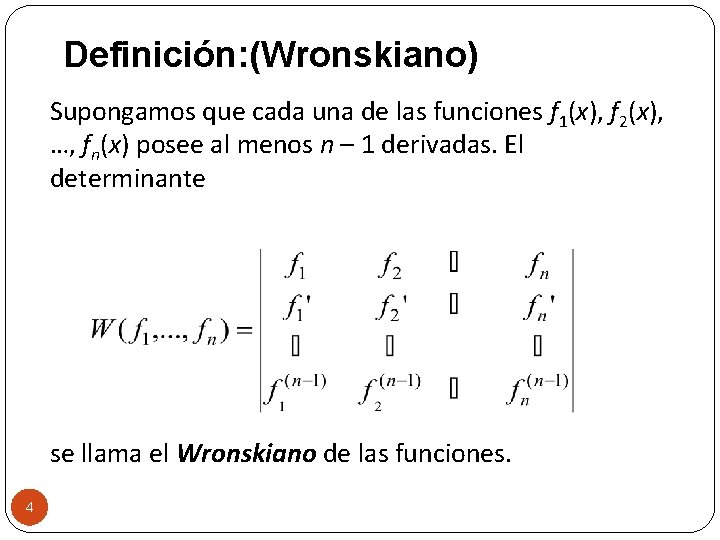
Definición: (Wronskiano) Supongamos que cada una de las funciones f 1(x), f 2(x), …, fn(x) posee al menos n – 1 derivadas. El determinante se llama el Wronskiano de las funciones. 4

Ejemplo 1: Las funciones y 1 = e 3 x, y 2 = e-3 x son soluciones de y” – 9 y = 0 en (- , ) Y el Wronskiano queda dado por:

• Ejemplo 2: Las funciones y 1 = ex, y 2 = e 2 x , y 3 = e 3 x. El Wronskiano queda dado por:

Método de variación de parámetros donde P(x), Q(x) y f(x) son continuas en I. Conocidas y 1(x) e y 2(x) soluciones l. i. de la ec. homogénea asociada, probaremos como solución particular: 7

Sustituimos yp’, yp” en la EDO: 0 8 0

Necesitaremos dos ecuaciones para encontrar valores de u 1 y u 2. Exijamos que: y 1 u 1’ + y 2 u 2’ = 0, para obtener una ecuación adicional y de paso que la EDO se reduzca a: y 1’u 1’ + y 2’u 2’ = f(x). De modo que nos queda el sistema de ecuaciones: y 1 u 1’ + y 2 u 2’ = 0 y 1’u 1’ + y 2’u 2’ = f(x) 9

Expresado en términos de determinantes y donde De donde encontraremos, por integración, las soluciones. 10

Solución: m 2 – 4 m + 4 = 0, m = 2 (cero doble) y 1 = e 2 x, y 2 = xe 2 x, Resolver Como f(x) = (x + 1)e 2 x, entonces: 11

Luego u 1 = (-1/3)x 3 – ½ x 2, u 2 = ½ x 2 + x Recordemos que: y 1 = e 2 x, y 2 = xe 2 x 12

Resolver Solución: y” + 9 y = (1/4) csc 3 x m 2 + 9 = 0, m = 3 i, -3 i y 1 = cos 3 x, y 2 = sin 3 x, f(x) = (1/4) csc(3 x) Como 13

Entonces 14

Resolver Solución: m 2 – 1 = 0, m = 1, -1 y 1 = ex, y 2 = e-x, f(x) = 1/x, y W(ex, e-x) = -2 Luego 15