Discrete Fourier Transform DFT JyhShing Roger Jang MIR


















- Slides: 35

Discrete Fourier Transform (DFT) Jyh-Shing Roger Jang (張智星) MIR Lab (多媒體資訊檢索實驗室) CSIE, NTU (台灣大學 資訊 程系) jang@mirlab. org, http: //mirlab. org/jang

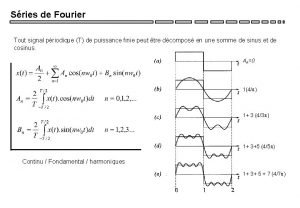
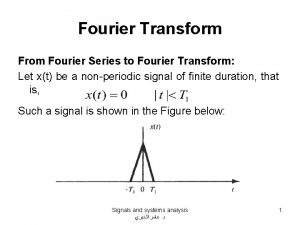
Discrete Fourier Transform z. Goal Due to sampling y. Decompose a given vector of discrete signals into sinusoidal components whose amplitudes can be view as energy distribution over a range of frequencies z. Applications y. Speech recognition y. Digital filtering y. Many more. . . -2 -

Decomposition z. How to decompose xn=x(n/fs), n=0~N-1 into a linear combination of sinusoidal functions? y. Magnitude spectrum y. Phase spectrum z. Remaining problems y. To determine no. of terms and their frequencies -3 -

How to Select Frequencies z. Signals of N points with sample rate fs y. Total duration d=N/fs (sec) y. Periods = d, d/2, d/3, … z. Freq. of sinusoids (bin frequencies) Total count = N/2+1 -4 -

No. of Terms for Decomposition z. Curve fitting for a parabola y# of unknowns = # of equations (= # of points) z. Curve fitting view for sinusoidal decomp. How many terms do we need if there are N points? N/2+1! -5 -

Example When N=4 -6 -

Example When N=8 -7 -

Sinusoidal Basis Functions (1/2) Can be converted into sin & cos Phase is necessary -8 -

Sinusoidal Basis Functions (2/2) -9 -

Decompose x(t) into Basis Functions n=0, 1, 2, …, N-1 # of terms = # of bin freq = N/2+1 # of fitting parameters = N -10 -

Decomposition into Basis Functions z. Overall expression: Amplitude Freq= Phase y. No. of parameters is 1+2*(N/2 -1)+1=N, which is equal to the no. of data points Exact solution is likely to exist. -11 -

Parameter Identification z. How to identify coefficients of the basis functions: y. Solving simultaneous linear equations y. Integration (which take advantage of the orthogonality of the basis functions) y. Fast Fourier transform (FFT) x. A fast algorithm with a complexity of O(N log N) -12 -

From Time-domain to Freq-domain z. Many animation over the web y 3 D animation Please post on FB if you find more. -13 -

Frequencies of Basis Functions z Due to Euler identity, we can express the k-th term shown on the right. Quiz! -14 -

Frequencies of Basis Functions z Plug in the simplified kth term: z Include the first and last terms: -15 -

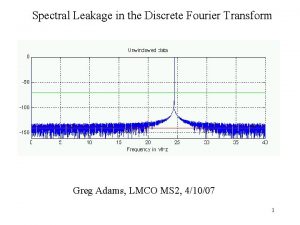
Representations of DFT: Two-side z. Characteristics y. General representation y. If x is complex, then c is not conjugate symmetric y. MATLAB command: c=fft(x) Usually complex numbers -16 -

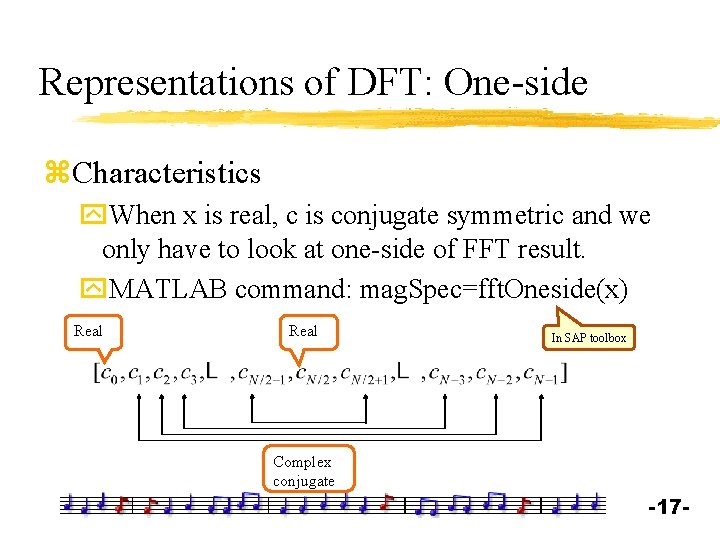
Representations of DFT: One-side z. Characteristics y. When x is real, c is conjugate symmetric and we only have to look at one-side of FFT result. y. MATLAB command: mag. Spec=fft. Oneside(x) Real In SAP toolbox Complex conjugate -17 -

Representations of DFT: One-side z. Formulas -18 -

-19 -

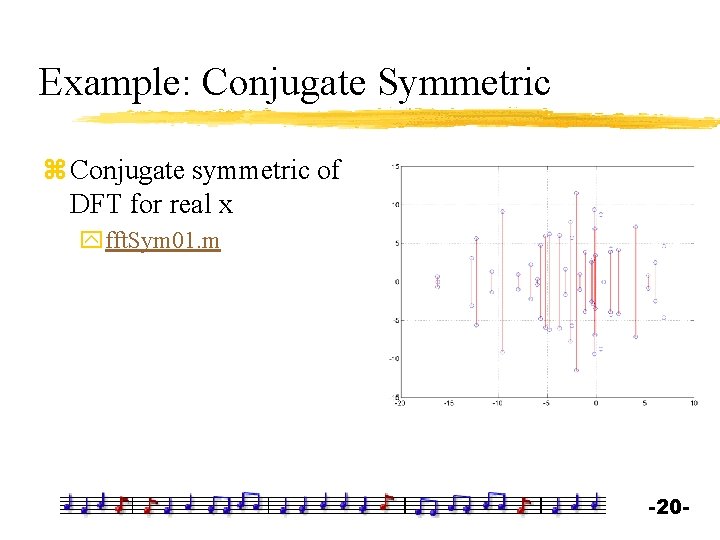
Example: Conjugate Symmetric z Conjugate symmetric of DFT for real x yfft. Sym 01. m -20 -

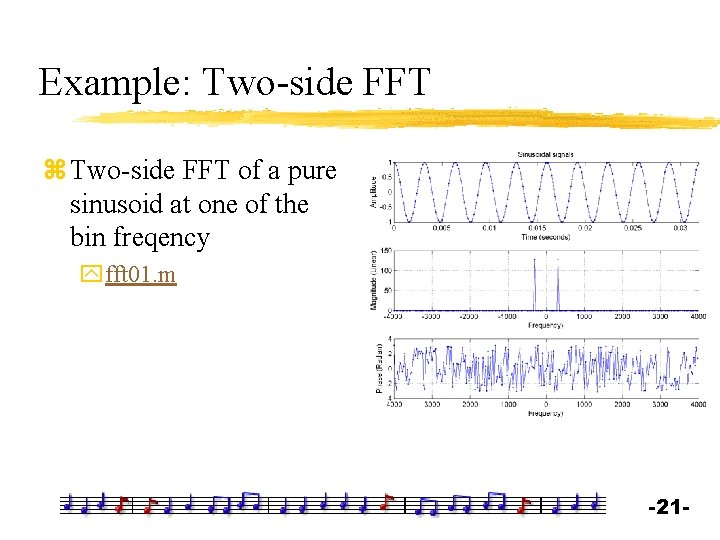
Example: Two-side FFT z Two-side FFT of a pure sinusoid at one of the bin freqency yfft 01. m -21 -

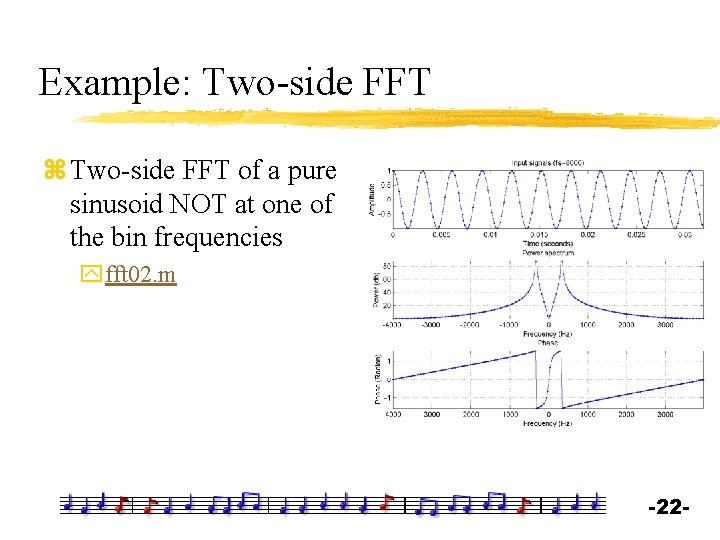
Example: Two-side FFT z Two-side FFT of a pure sinusoid NOT at one of the bin frequencies yfft 02. m -22 -

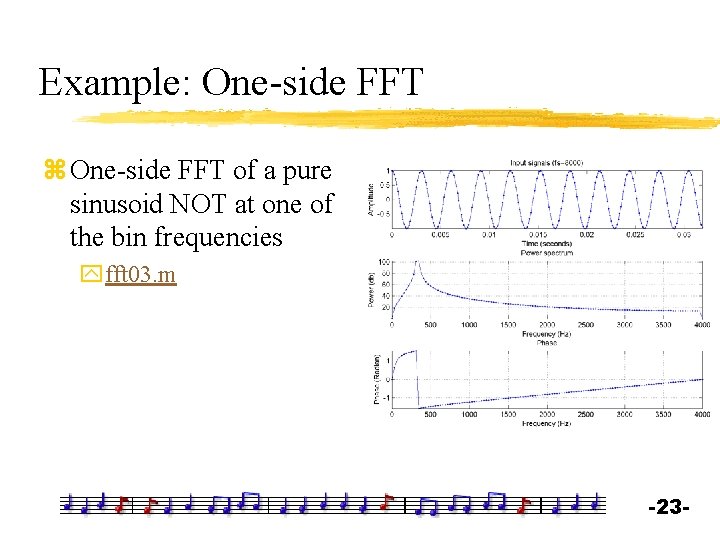
Example: One-side FFT z One-side FFT of a pure sinusoid NOT at one of the bin frequencies yfft 03. m -23 -

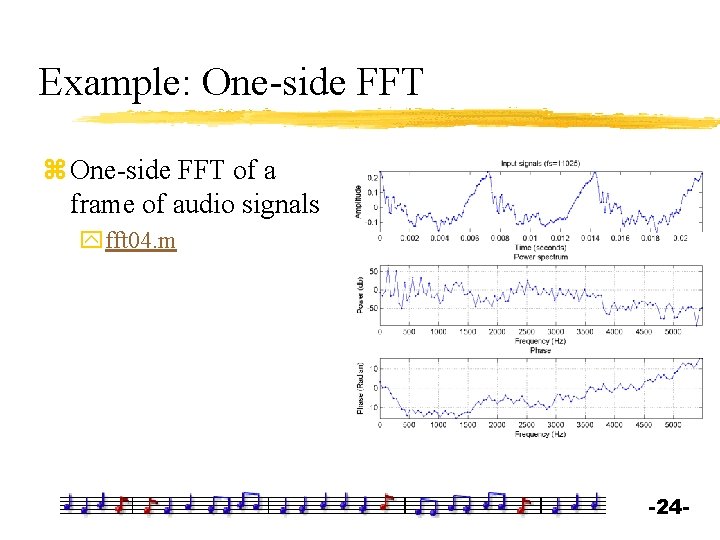
Example: One-side FFT z One-side FFT of a frame of audio signals yfft 04. m -24 -

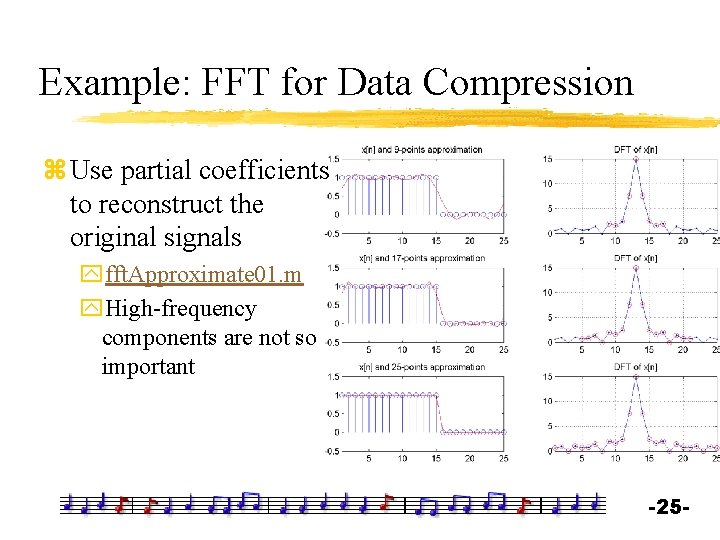
Example: FFT for Data Compression z Use partial coefficients to reconstruct the original signals yfft. Approximate 01. m y. High-frequency components are not so important -25 -

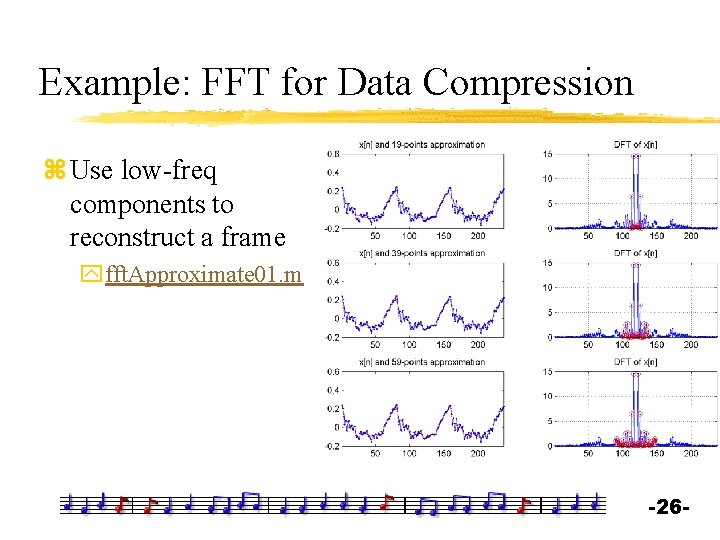
Example: FFT for Data Compression z Use low-freq components to reconstruct a frame yfft. Approximate 01. m -26 -

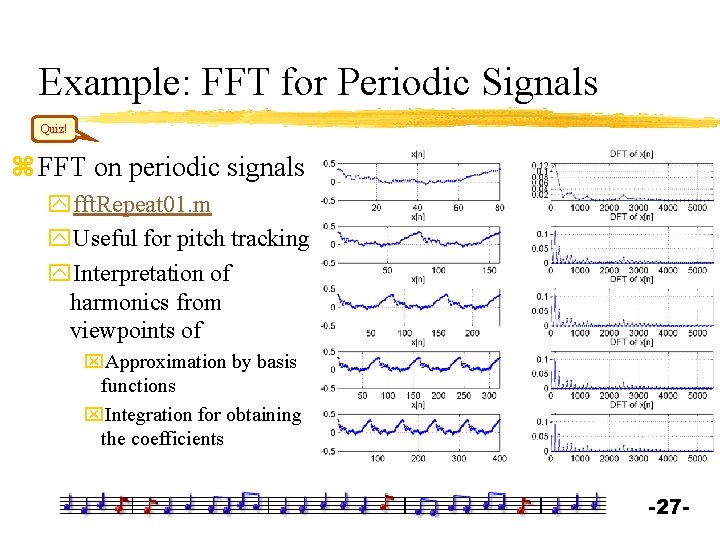
Example: FFT for Periodic Signals Quiz! z FFT on periodic signals yfft. Repeat 01. m y. Useful for pitch tracking y. Interpretation of harmonics from viewpoints of x. Approximation by basis functions x. Integration for obtaining the coefficients -27 -

Why Harmonic Structures? -28 -

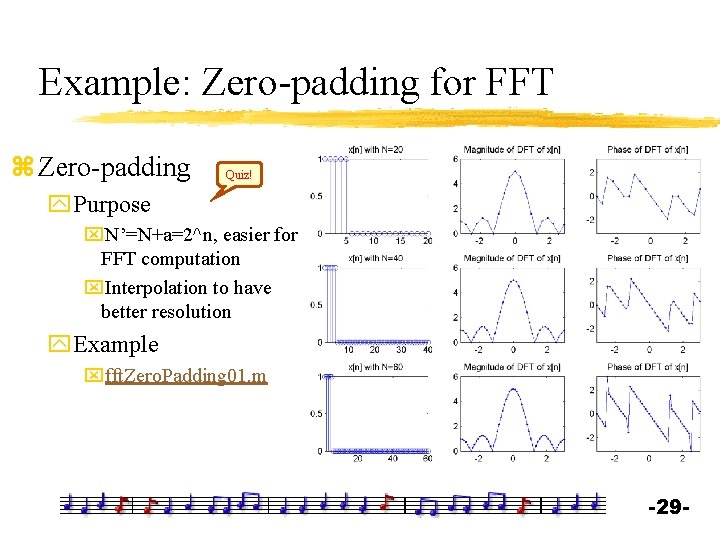
Example: Zero-padding for FFT z Zero-padding Quiz! y. Purpose x. N’=N+a=2^n, easier for FFT computation x. Interpolation to have better resolution y. Example xfft. Zero. Padding 01. m -29 -

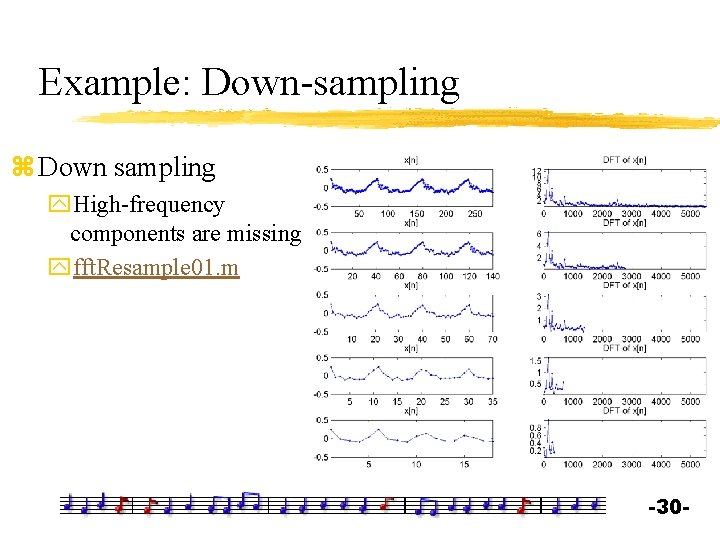
Example: Down-sampling z Down sampling y. High-frequency components are missing yfft. Resample 01. m -30 -

Harmonics z. Why do we have harmonic structures in a power spectrum? y. Since the original frame is quasi-periodic… z. If we want to use the spectrum for pitch tracking, we need to enhance the harmonics. How? -31 -

How to Enhance Harmonics? z. Goal y. Enhance harmonics for pitch tracking z. Approach y. Take an integer number of fundamental periods Hard! y. Use windowing y. Use zero-padding for better resolution -32 -

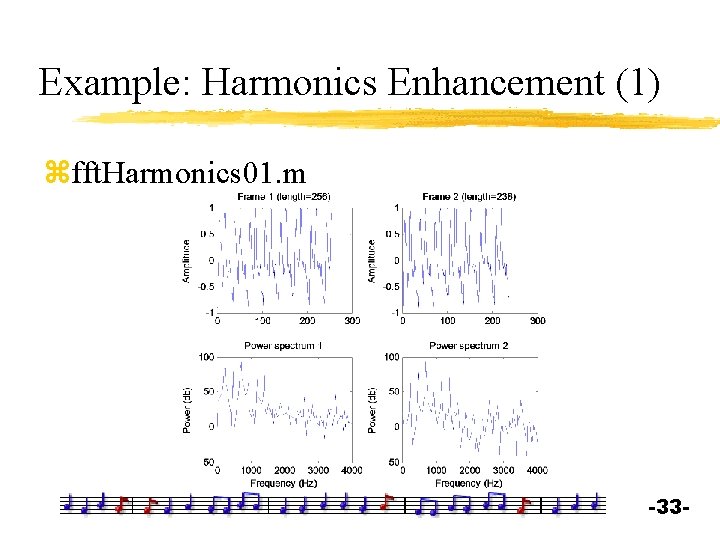
Example: Harmonics Enhancement (1) zfft. Harmonics 01. m -33 -

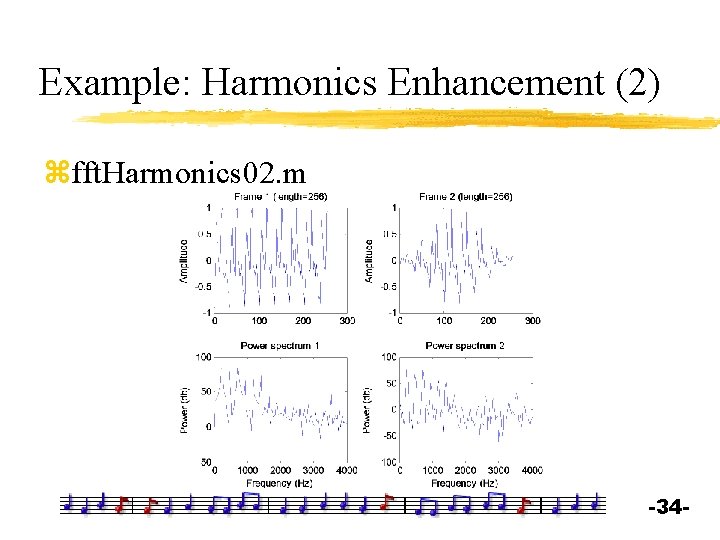
Example: Harmonics Enhancement (2) zfft. Harmonics 02. m -34 -

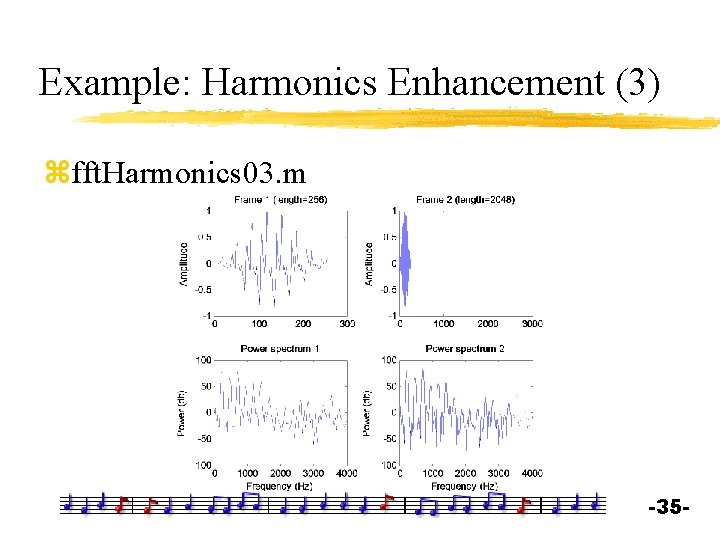
Example: Harmonics Enhancement (3) zfft. Harmonics 03. m -35 -
 Roger jang
Roger jang 2d discrete fourier transform
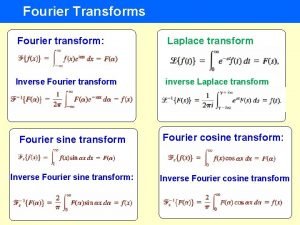
2d discrete fourier transform Fourier transform formula
Fourier transform formula Discrete fourier transform
Discrete fourier transform Discrete fourier transform formula
Discrete fourier transform formula Discrete fourier transform formula
Discrete fourier transform formula Application of discrete fourier transform
Application of discrete fourier transform Discrete fourier transform of delta function
Discrete fourier transform of delta function What is dft
What is dft Dtft symmetry property
Dtft symmetry property Comb function matlab
Comb function matlab Mir pravi mir daje krist gospodin naš
Mir pravi mir daje krist gospodin naš Magnitude and phase response
Magnitude and phase response Spectre signal echantillonné
Spectre signal echantillonné Fourier analysis of discrete time signals
Fourier analysis of discrete time signals Discrete time fourier series
Discrete time fourier series Discrete cosine transform formula
Discrete cosine transform formula Fast discrete cosine transform
Fast discrete cosine transform Wavelet transform image
Wavelet transform image Dct
Dct Jang
Jang Jumping jang
Jumping jang Jinho jang
Jinho jang Jang
Jang Berkay bahadur
Berkay bahadur Yeongjin jang
Yeongjin jang Yeongjin jang
Yeongjin jang Jang multimedia
Jang multimedia Jang
Jang Dr helen jang
Dr helen jang Language model
Language model Inverse fourier transform
Inverse fourier transform Inverse of fourier transform
Inverse of fourier transform Fourier transform properties examples
Fourier transform properties examples Sine integral
Sine integral Fourier series coefficients formula
Fourier series coefficients formula