Digital Signal Processing Tomography Introduction Frequently used in

Digital Signal Processing Tomography

Introduction • • Frequently used in medical applications Acoustics Microwaves Geology Electronic Microscopes Radio telescopes X-ray computed tomography

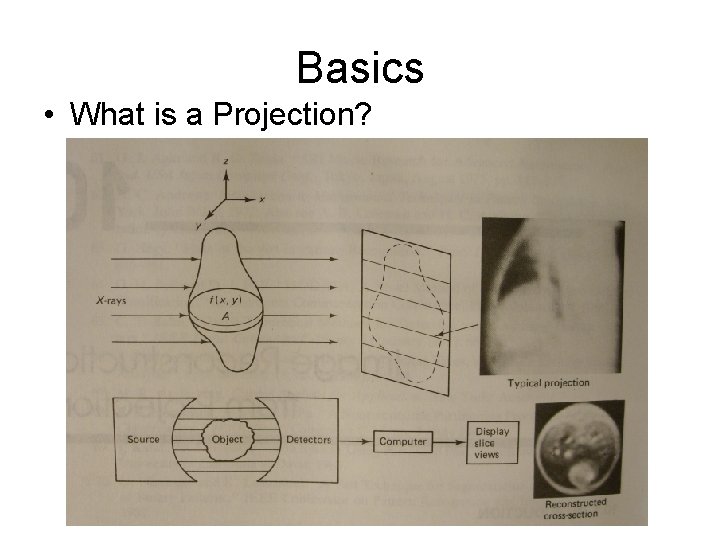
Basics • What is a Projection?

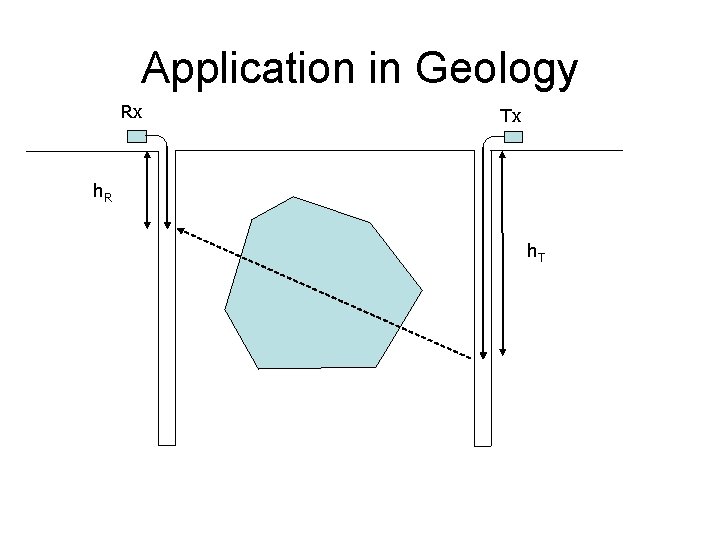
Application in Geology Rx Tx h. R h. T

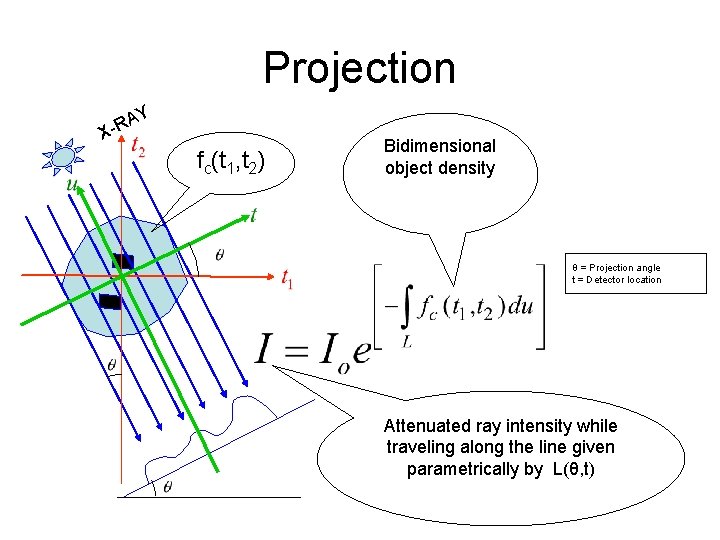
Projection Y A R X fc(t 1, t 2) Bidimensional object density θ = Projection angle t = Detector location Attenuated ray intensity while traveling along the line given parametrically by L(θ, t)

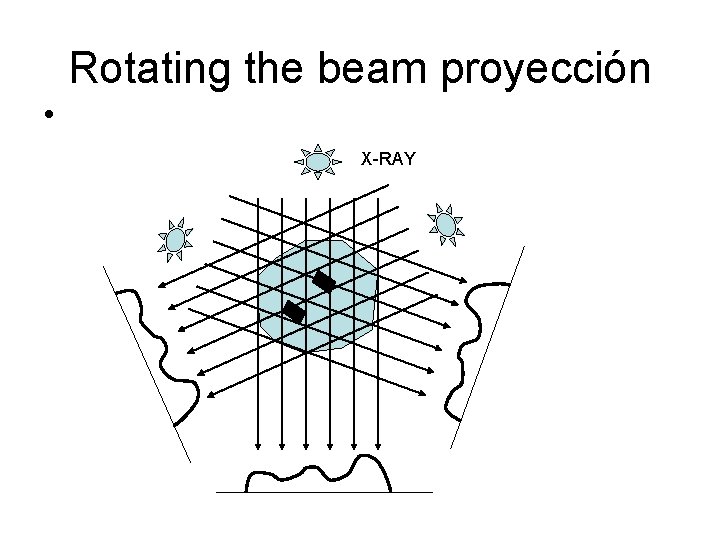
Rotating the beam proyección • X-RAY

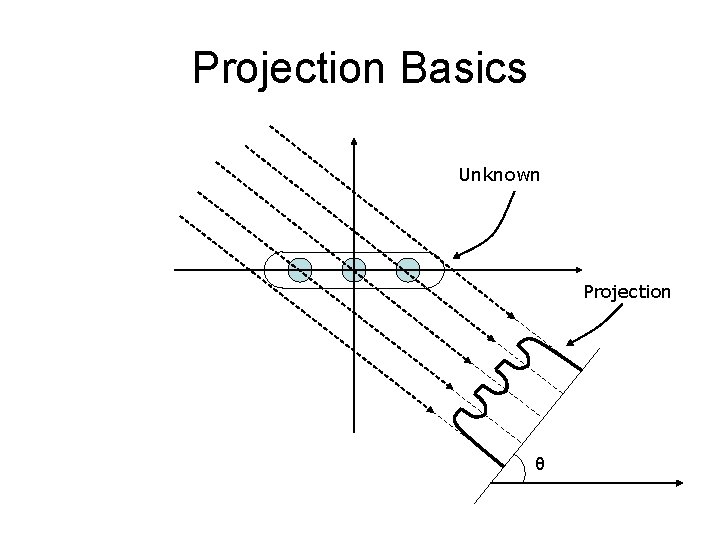
Projection Basics Projection refers to the way the x-ray beam, like an arrow, passes through an object and creates an image (projection) on a photographic film. Our objective is to reconstruct the two dimensional object from the different projections obtained when the beam is rotated

Projection Basics Unknown Projection θ

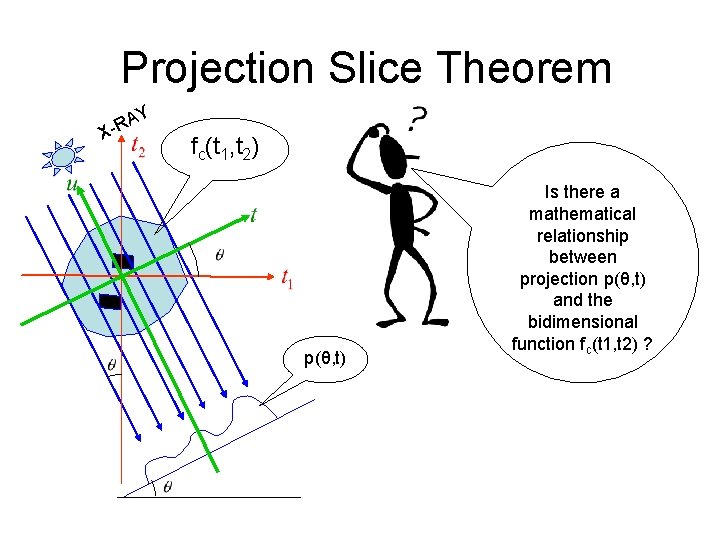
Projection Slice Theorem Y A R X fc(t 1, t 2) p(θ, t) Is there a mathematical relationship between projection p(θ, t) and the bidimensional function fc(t 1, t 2) ?

Projection Slice Theorem

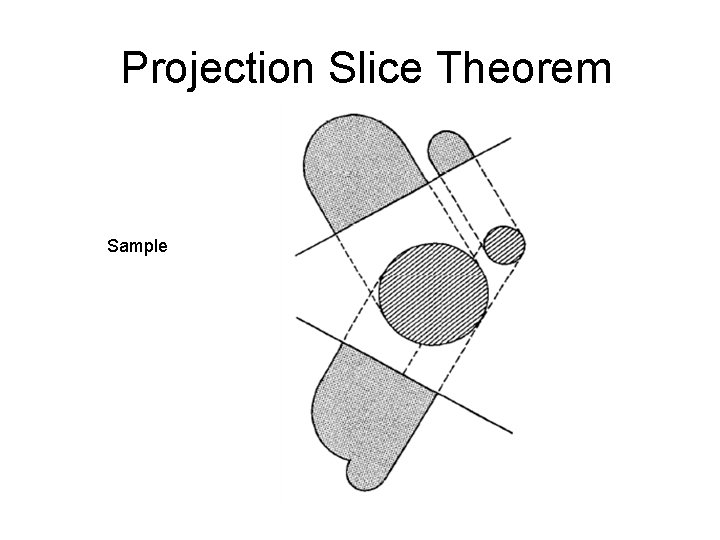
Projection Slice Theorem Sample

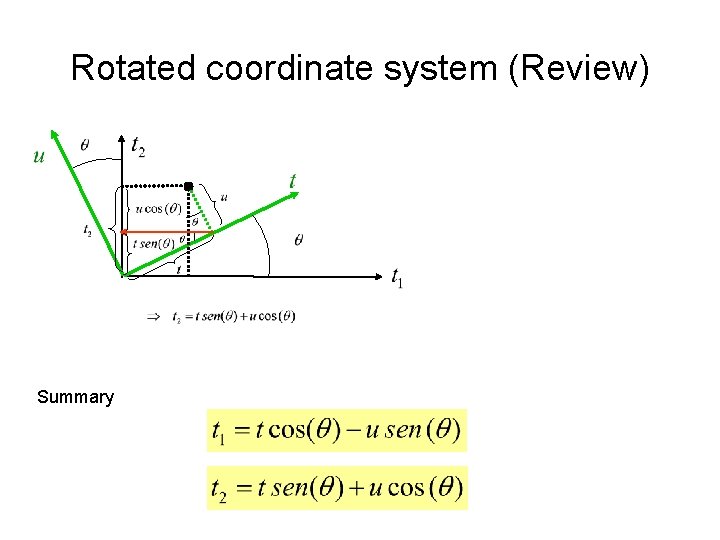
Rotated coordinate system (Review)

Rotated coordinate system (Review) Summary

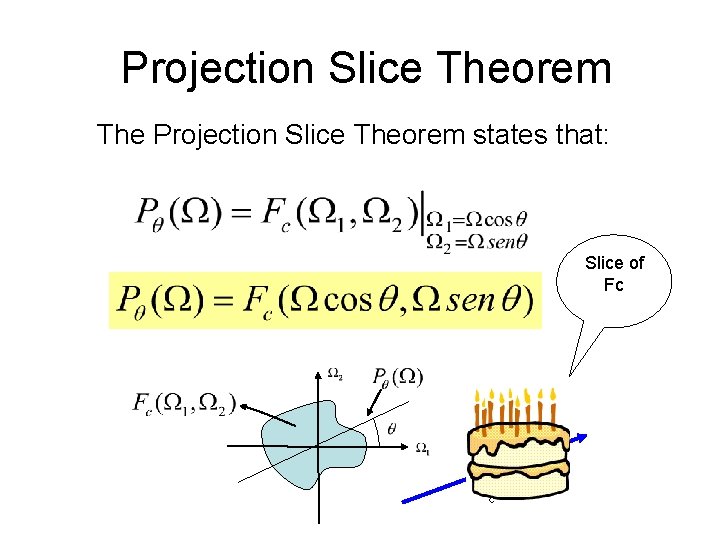
Projection Slice Theorem From now on our aim is to find a relationship between the two dimensional FT of fc(t 1, t 2) and the one dimensional FT of p(θ, t). This can be carried out by using the Projection Slice Theorem

Projection Slice Theorem Lets start finding the 2 D CTFT from fc(t 1, t 2) We also know that the 2 D CIFT of Fc(Ω 1Ω 2) is:

Projection Slice Theorem On the other hand the TF 1 D de p(θ, t) is:

Projection Slice Theorem The Projection Slice Theorem states that: Slice of Fc

Projection Slice Theorem This theorem is very useful to our purpose since taking projections at different angles we can reconstruct the TF of fc(t 1, t 2). Afterwards taking the inverse transform we can obtain the original object.

Reconstruction methods 1. 2. 3. Simple : - Nearest Neighbor (zero order interpolation) - First order interpolation. Radon inversión formula Iterative methods

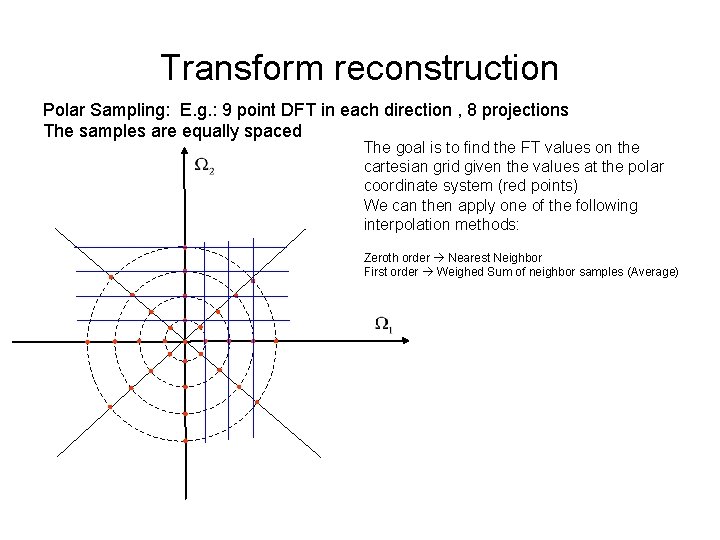
Transform reconstruction Polar Sampling: E. g. : 9 point DFT in each direction , 8 projections The samples are equally spaced The goal is to find the FT values on the cartesian grid given the values at the polar coordinate system (red points) We can then apply one of the following interpolation methods: Zeroth order Nearest Neighbor First order Weighed Sum of neighbor samples (Average)

Transform reconstruction If we change the samples as a function of the projection angle we obtain concentric squares

Radon Inversion Formula Recall that IDFT 2 D of Fc(Ω 1, Ω 2) is: We can express this expression using polar coordinates: i. e. : (Ω 1, Ω 2) (ω, θ).

Radon Inversion Formula To accomplish this we need the jacobian:

Radon Inversion Formula Therefore fc(t 1, t 2) will be:

Formula de inversion de Radon Then we have:

Formula de inversion de Radon The second integral is an IDFT: IDFT

Formula de inversion de Radon This gives us: Substituting in fc(t 1, t 2) we have:

Formula de inversion de Radon Finally:

Formula de inversion de Radon Summary: 1 - Find 2 - Evaluate 3 - Substitute in fc(t 1, t 2)

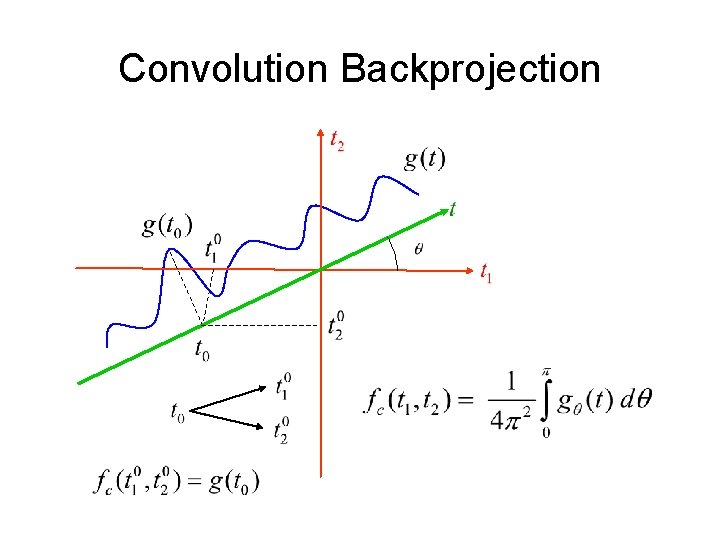
Convolution Backprojection

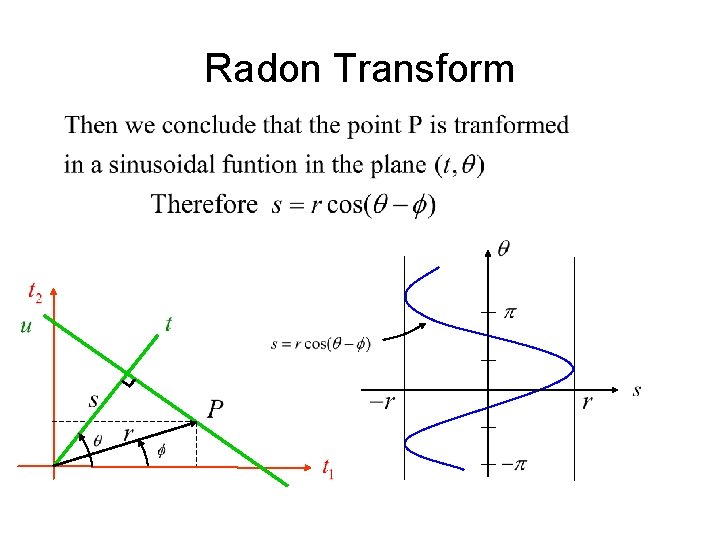
Radon Transform

Radon Transform

Radon Transform

Radon Transform

Matlab Support Example: Matlab code to obtain projections from an image

Matlab Support We can see the transform for all the angles in one image

Matlab Support INVERSE RADON TRANSFORM Now we can reconstruct the image from the projections.

Matlab Support