UnitV MULTIRATE DIGITAL SIGNAL PROCESSING Multirate Digital Signal

Multi-rate Digital Signal Processing Basic Sampling Rate Alteration Devices • Up-sampler - Used to

Down-Sampler Time-Domain Characterization • An down-sampler with a down-sampling factor M, where M is

Down-Sampler • Down-sampling operation is implemented by keeping every M-th sample of x[n] and

Decimation by a factor D In downsampling by an integer factor D>1, every D-th

Decimation by a factor D l Relationship in time domain Input sequence Periodic train

Decimation by a factor D l Relationship in frequency domain C

Decimation by a factor D l Using a digital low-pass filter to prevent aliasing

Up-Sampler Time-Domain Characterization • An up-sampler with an up-sampling factor L, where L is

Up-Sampler • Up-sampling operation is implemented by inserting equidistant zerovalued samples between two consecutive

Up-Sampler • In practice, the zero-valued samples inserted by the up-sampler are replaced with

Interpolation by a factor I In up-sampling by an integer factor I >1, I

Interpolation by a factor I Relationship in frequency domain Input sequence

Sampling rate conversion by a rational factor I/D If is a rational number I

Slides: 33

Download presentation

Unit-V MULTI-RATE DIGITAL SIGNAL PROCESSING

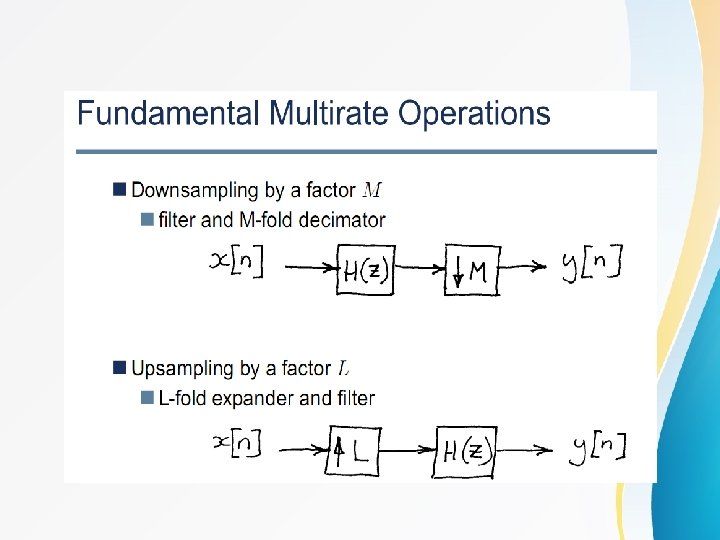
Multi-rate Digital Signal Processing Basic Sampling Rate Alteration Devices • Up-sampler - Used to increase the sampling rate by an integer factor • Down-sampler - Used to decrease the sampling rate by an integer factor

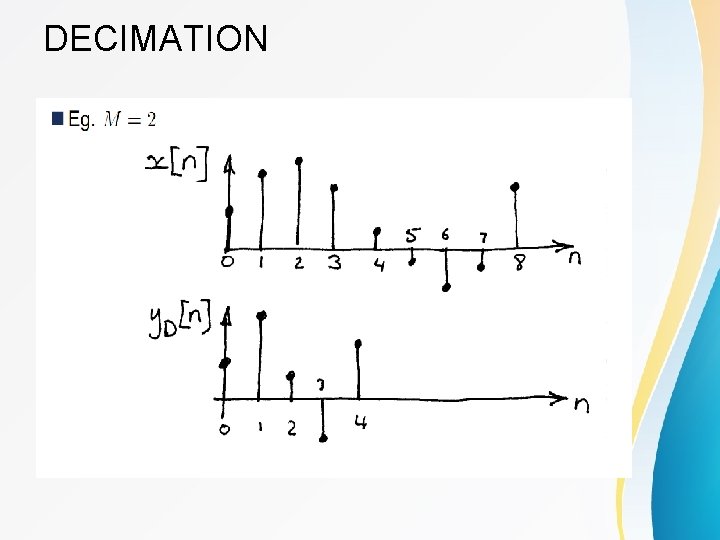
DECIMATION

Down-Sampler Time-Domain Characterization • An down-sampler with a down-sampling factor M, where M is a positive integer, develops an output sequence y[n] with a sampling rate that is (1/M)-th of that of the input sequence x[n] • Block-diagram representation x[n] M y[n]

Down-Sampler • Down-sampling operation is implemented by keeping every M-th sample of x[n] and removing inbetween samples to generate y[n] • Input-output relation y[n] = x[n. M]

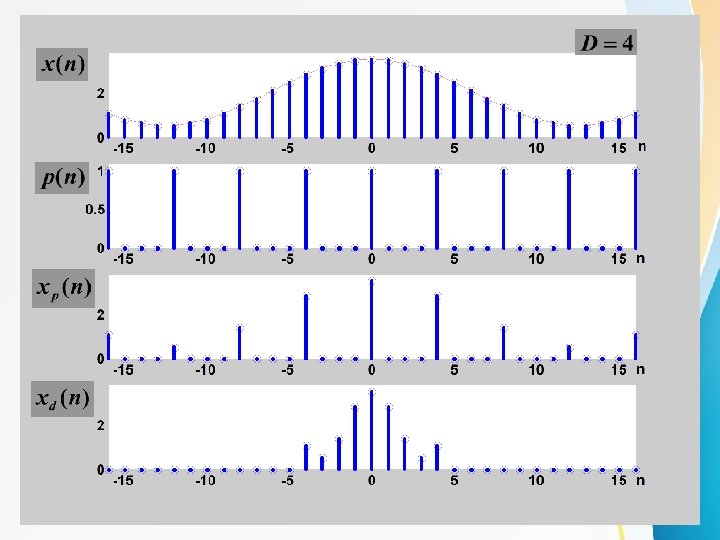
Decimation by a factor D In downsampling by an integer factor D>1, every D-th samples of the input sequence are kept and others are removed: D

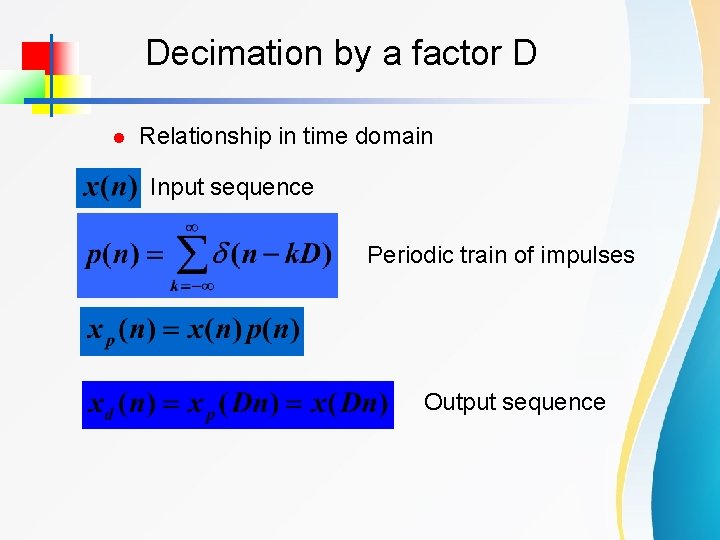
Decimation by a factor D l Relationship in time domain Input sequence Periodic train of impulses Output sequence

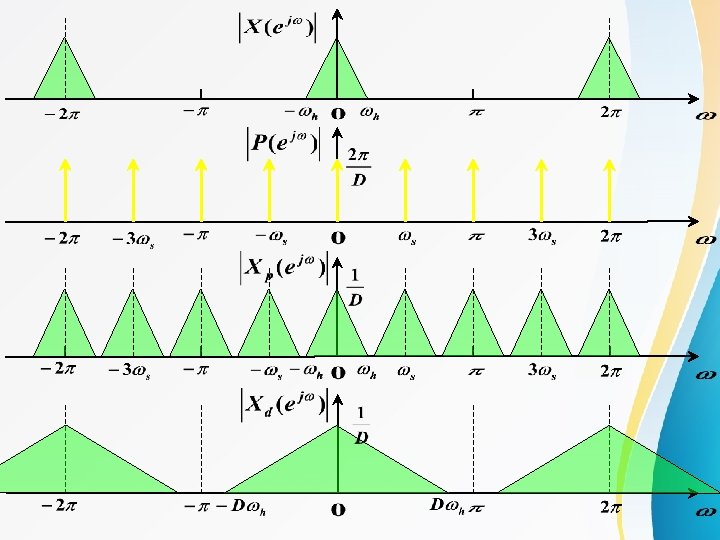
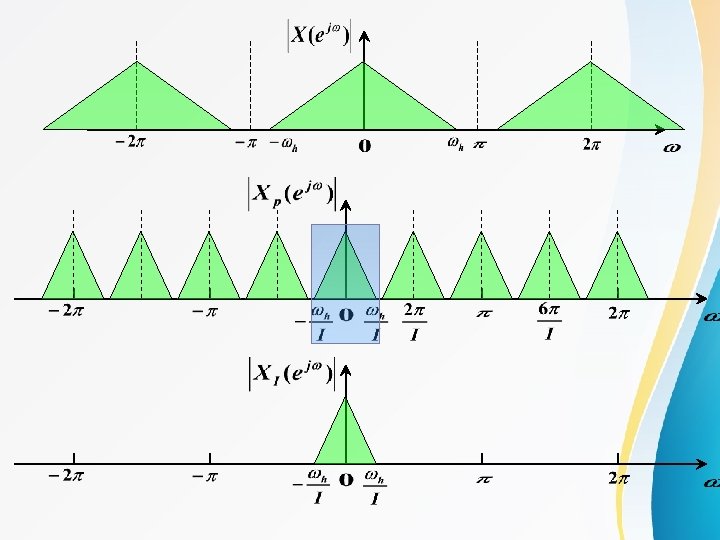
Decimation by a factor D l Relationship in frequency domain C

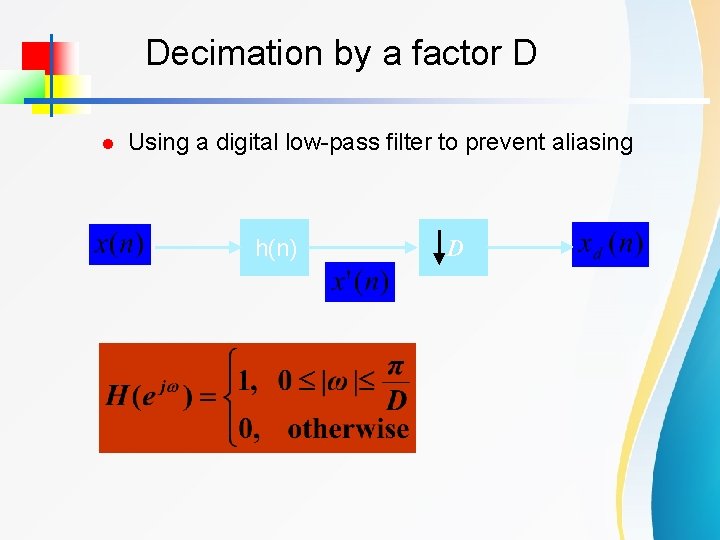
Decimation by a factor D l Using a digital low-pass filter to prevent aliasing h(n) D

INTERPOLATION

Up-Sampler Time-Domain Characterization • An up-sampler with an up-sampling factor L, where L is a positive integer, develops an output sequence with a sampling rate that is L times larger than that of the input sequence x[n] • Block-diagram representation x[n] L

Up-Sampler • Up-sampling operation is implemented by inserting equidistant zerovalued samples between two consecutive samples of x[n] • Input-output relation

Up-Sampler • In practice, the zero-valued samples inserted by the up-sampler are replaced with appropriate nonzero values using some type of filtering process • Process is called interpolation and will be discussed later

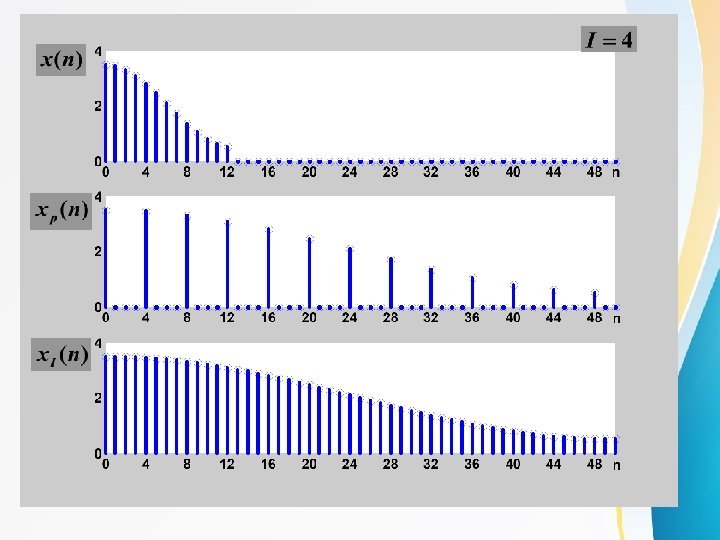
Interpolation by a factor I In up-sampling by an integer factor I >1, I -1 equidistant zeros-valued samples are inserted between each two consecutive samples of the input sequence. Then a digital low-pass filter is applied. I h(n)

Interpolation by a factor I Relationship in frequency domain Input sequence

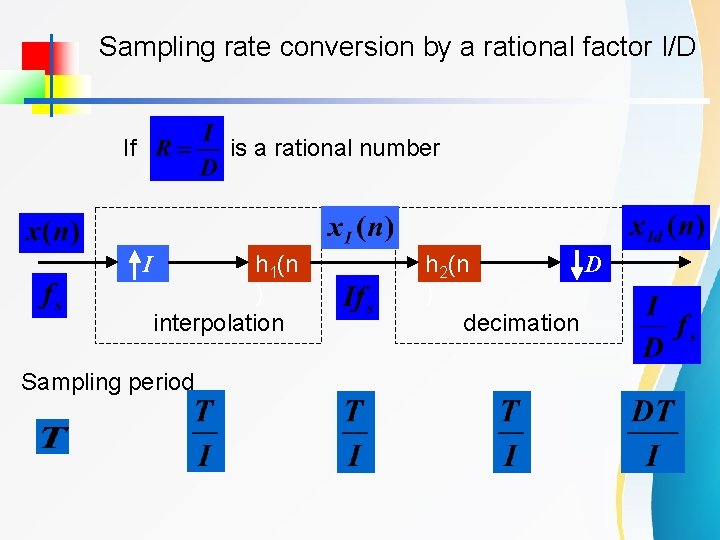
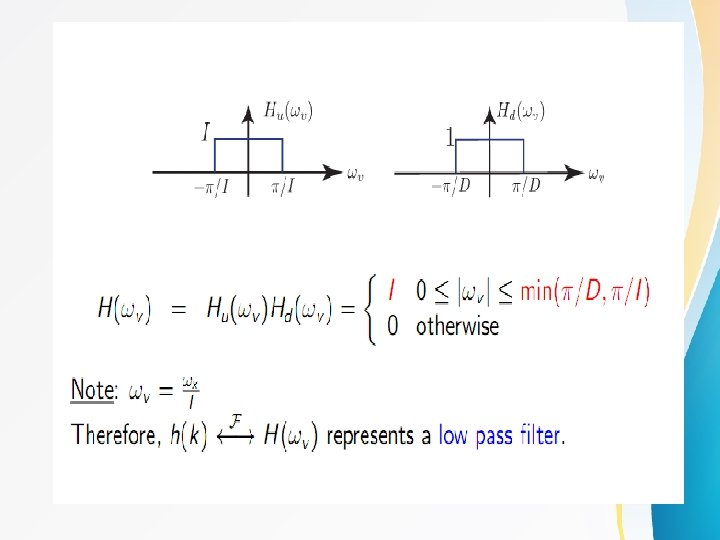
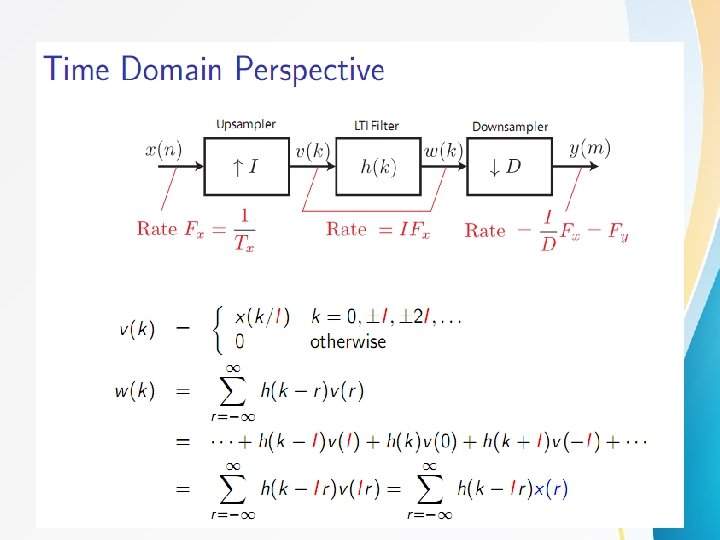
Sampling rate conversion by a rational factor I/D If is a rational number I h 1(n ) interpolation Sampling period D h 2(n ) decimation

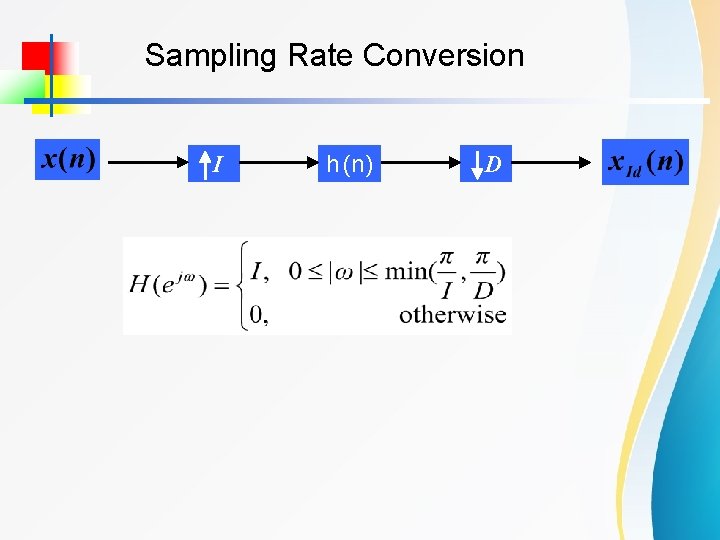
Sampling Rate Conversion I h (n) D