Diferentes Formas Funcionales y Otras Cosas del Analisis

Diferentes Formas Funcionales y Otras Cosas del Analisis de Regresion + Un poco de repaso

El significado de los coeficientes de regresión: E(Y| X 2, X 3) = 1 + 2 X 2 + 3 X 3 E(Y|X 2, X 3) X 2 = 2 : 2 mide el cambio en el valor medio de Y, por un cambio de una unidad en X 2, manteniendo X 3 constante. o E(Y|X 2, X 3) = X 3 El efecto ‘directo’ de un cambio en una unidad en X 2 sobre el valor medio de Y, neto de X 3. 3 ? ? ?

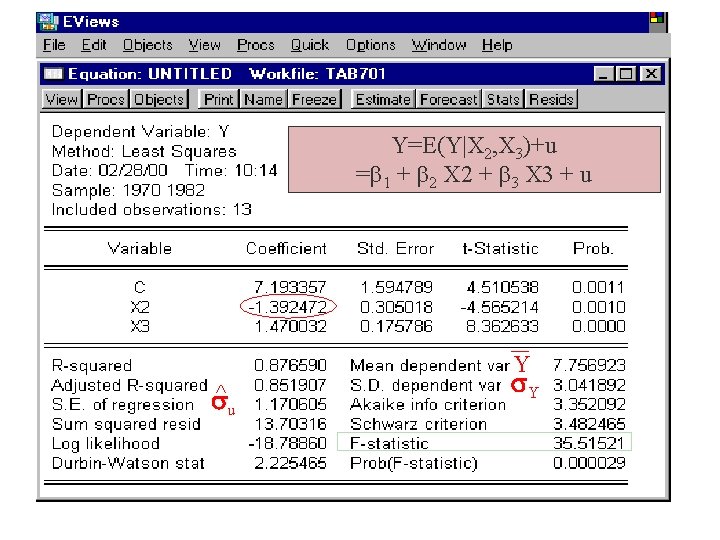
Y=E(Y|X 2, X 3)+u = 1 + 2 X 2 + 3 X 3 + u Y ^ u Y

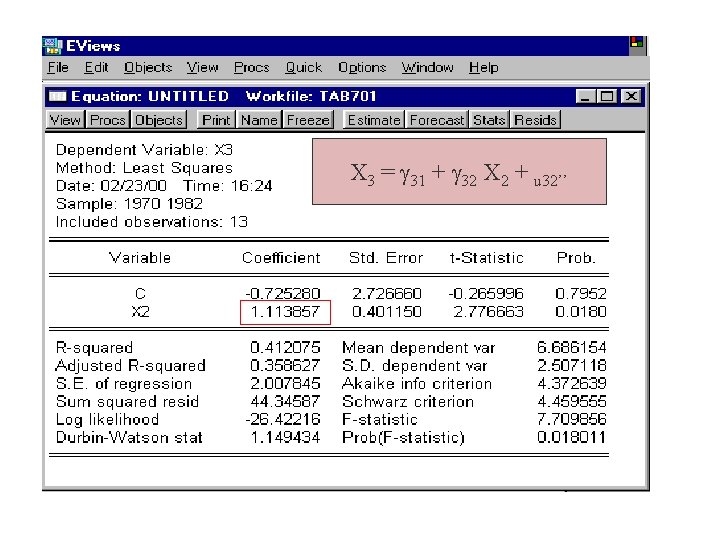
. 39 25 -1 X 2 22 X 2 = + u 2 2 = de to ec dir + = 2 X X 3 Y de 12 to 2 , X 3) to X ec ec 0 70 3 X 3 = g 31 + g 32 X 2 + u 23 dir +u X 2 = g 21 + g 23 X 3 + u 23 1. 4 X 3 23 (Y | to + Tasa de Paro(%) fec 3 13 X 2 E ) = , X 3 3 |X 2 = (Y X = Ef E Y Y E Tasa de inflacion actual(%) X 3 Tasa de inflacion esperada (%) X 3 = g 32 = 1. 1138 X 2 Efecto indirecto via X 3

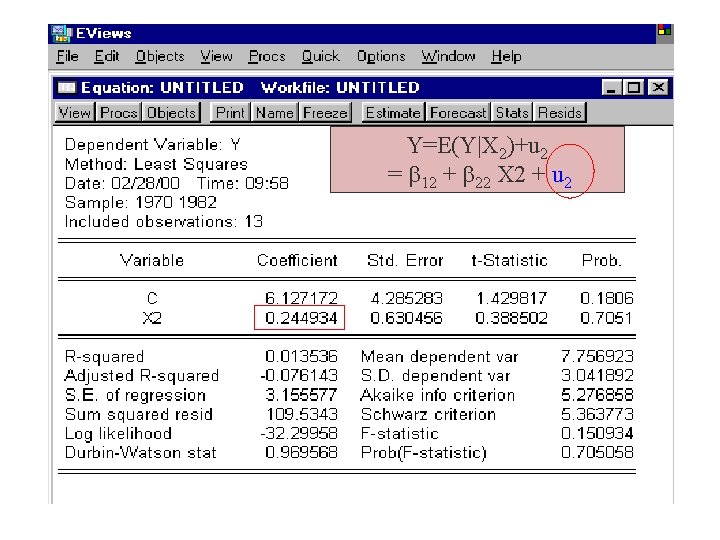
Efecto total de X 2 sobre E(Y|X 2, X 3): 2 + 3 * g 32 = -1. 392472 + (1. 470032)(1. 11385) ‘directo’ + ‘indirecto’= -1. 392472 + 1. 637395 = 0. 244923 Y X 2 E(Y| X 2 )= 12+ 22 X 2 E(Y|X 2) X 2 = 22 = 0. 2449

Y=E(Y|X 2)+u 2 = 12 + 22 X 2 + u 2

X 3 = g 31 + g 32 X 2 + u 32’’

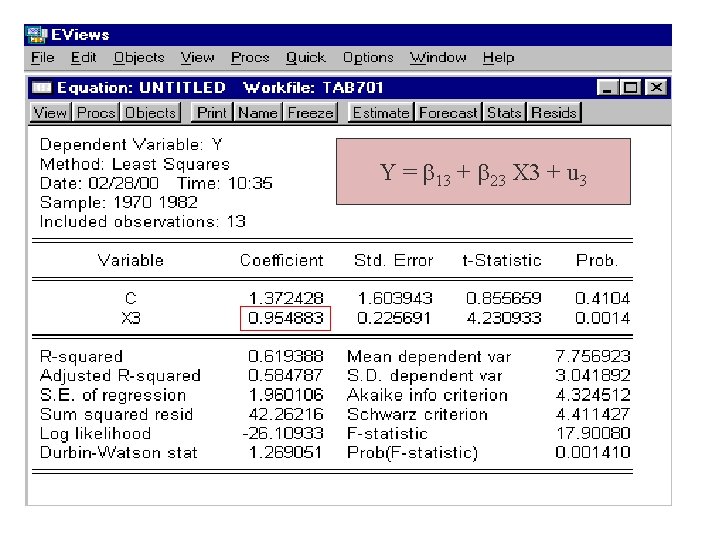
Efecto total de X 3 sobre E(Y|X 2, X 3): 3 + 2 * g 23 = 1. 470032 + (-1. 392472) (0. 369953) ‘directo’ + ‘indirecto’ = 1. 470032 - 0. 515149 = 0. 9548828 Y X 3 Y = 13 + 23 X 3 + u 3 E(Y|X 3) X 3 = 23 = 0. 954883

X 2 = g 21 + g 23 X 3 + u 23

Y = 13 + 23 X 3 + u 3

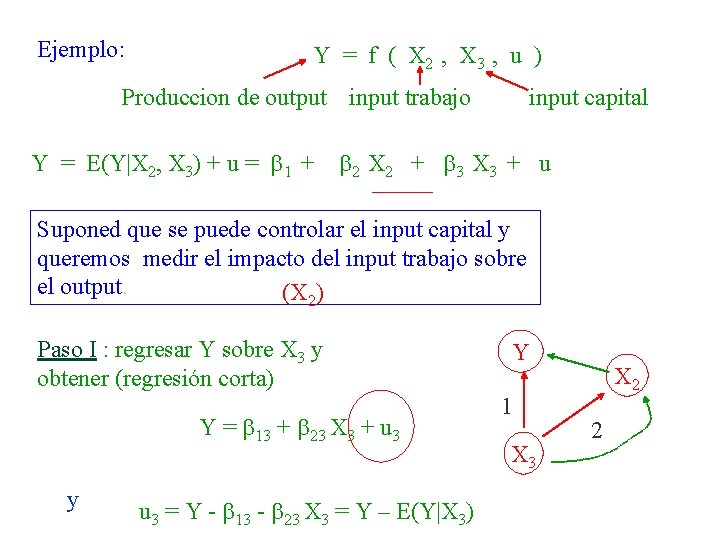
Ejemplo: Y = f ( X 2 , X 3 , u ) Produccion de output input trabajo Y = E(Y|X 2, X 3) + u = 1 + input capital 2 X 2 + 3 X 3 + u Suponed que se puede controlar el input capital y queremos medir el impacto del input trabajo sobre el output. (X 2) Paso I : regresar Y sobre X 3 y obtener (regresión corta) Y = 13 + 23 X 3 + u 3 y u 3 = Y - 13 - 23 X 3 = Y – E(Y|X 3) Y 1 X 3 X 2 2

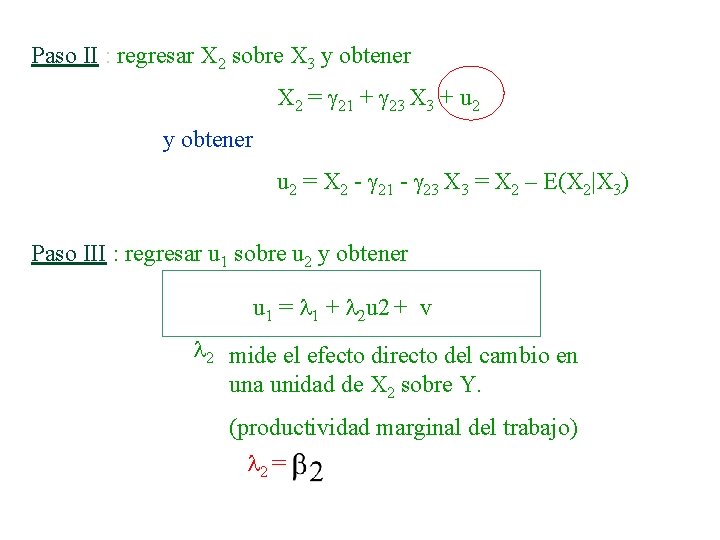
Paso II : regresar X 2 sobre X 3 y obtener X 2 = g 21 + g 23 X 3 + u 2 y obtener u 2 = X 2 - g 21 - g 23 X 3 = X 2 – E(X 2|X 3) Paso III : regresar u 1 sobre u 2 y obtener u 1 = l 1 + l 2 u 2 + v l 2 mide el efecto directo del cambio en una unidad de X 2 sobre Y. (productividad marginal del trabajo) l 2 =

EJEMPLOS DE MODELOS LINEALES Ejemplo 1: Capital Asset Pricing Model (CAPM) para la accion i’s ( ER i Tasa esperada de rendimiento de la accion i - r f )= b 2 ( ER Rendimiento de un activo libre de riesgo m f Tasa esperada de rendimiento de la cartera del mercado b 2 Como medida del riesgo sistematico b 2 >1 ==> una accion volatil o agresiva b 2 <1 ==> una accion defensiva - r )

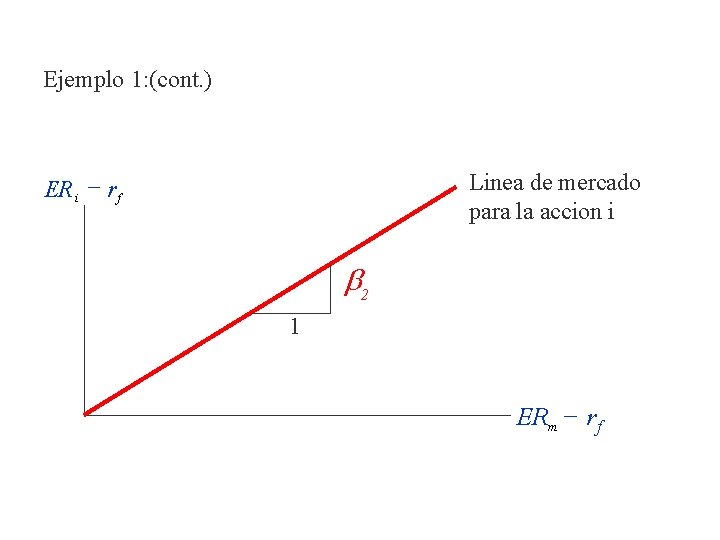
Ejemplo 1: (cont. ) Linea de mercado para la accion i ER i - r f b 2 1 ERm - rf

Ejemplo 2: Paridad encubierta de los tipos de interes FN - e = f. N (i - i ) = e * Los diferenciales internacionales en las tasas de interes deben ser iguales a la prima del tipo de cambio (forward). i. e. , - e F (i - i ) = 2 ( ) e * Linea de la paridad encubierta de los tipos de interes b 2 1

Ejemplo 2: (Cont. ) en la regresion: F -e (i - i ) = b 1 + b 2( ) + ui e * Si la teoria de la paridad encubierta es cierta, 1=0 y 2=1 Todavia estamos en la etapa de entender a interpretar los coeficientes de una regresión. MUY PRONTO aprenderemos a contrastar diferentes hipótesis sobre los valores de los coeficientes; pero PRIMERO LO PRIMERO (First things First)

Formas Funcionales de la Regresion El termino lineal en un modelo de regresion simple significa que es lineal en los parametros; pero en las variables de la regresion puede ser lineal o no. Definición: Una función es lineal en alguno de sus argumentos si la primera derivada parcial de la función con respecto dicho argumento no contiene este argumento.

Lineal vs. Nonlineal Ejemplos de Modelos Lineales Yi = 1 + 2 Xi + ui ln(Yi) = 1 + 2 Xi + ui Yi = 1 + 2 ln(Xi) + ui Yi = 1 + 2 X 2 i + ui Ejemplos de Modelos No-Lineales Yi = 1 + 3 2 X i + ui 3 Yi = 1 + 2 Xi + ui Yi = 1 + 2 Xi + exp( 3 Xi) + ui

Diferentes Formas Funcionales 1. Lineal 2. Log-Log 3. Semilog Lineal-Log Log-Lineal 4. Reciproca Presta Atencion a la pendiente y a la elasticidad de cada una de las formas

Formas Funcionales de los modelos de regresion 1. Modelo log-log : Y= b 1 X - 2 e Este es un modelo no-lineal ui Tomando Logs lo convertimos en lineal : ln Y= ln 1 - 2 ln X+ ui ==> ln Y= 1 - 2 ln X+ ui ==> Y = 1 + 2 X + ui * * d. Y* d. X* * d. Y d ln Y = = Y d. X d ln X X * donde b 2 = - b 2 = 2* Coef de elasticidad

Cantidad Demandada Formas Funcionales de los modelos de regresion ln. Y Y Y = b 1 X -b 2 X precio ln Y= ln 1 - 2 ln. X

Formas Funcionales de los modelos de regresion 2. Modelo Semi log: Modelo Log-lineal o lineal-log: ln Yi = a 1 + a 2 X i + ui o Yi = b 1 + b 2 ln Xi + ui a 2 = y b 2 = d. Y Cambio relativo en y d ln Y d. Y 1 = = Y = d. X Y Cambio absoluto en x Cambio absoluto en y Cambio relativo en x = d. Y = d. X d ln X X 1

Formas Funcionales de los modelos de regresion (cont) 3. Transformacion reciproca o inversa 1 Yi = b 1 + b 2 ( ) + ui Xi ==> Yi = b 1 + b 2 ( Xi ) + u i * donde Xi = * 1 Xi

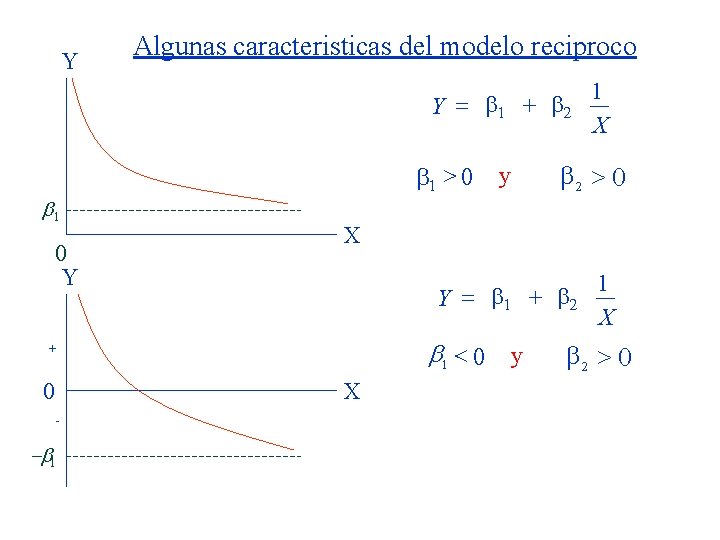
Y Algunas caracteristicas del modelo reciproco Y = 1 + 2 b 1 0 Y 1 > 0 Y = 1 + 2 b 1 < 0 y X - -b 1 2 > 0 X + 0 y 1 X 2 > 0

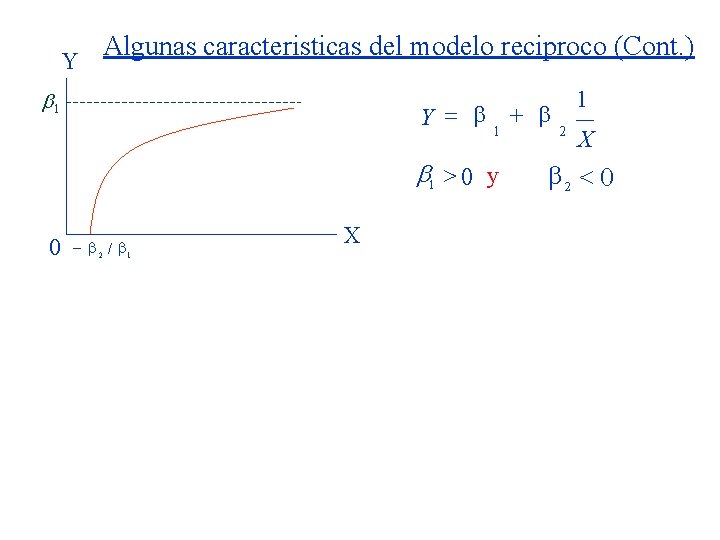
Y Algunas caracteristicas del modelo reciproco (Cont. ) b 1 Y = 1 + b 1 > 0 y 0 - 2 / 1 X 1 2 X 2 < 0

Ejemplo 1: Sea transformando Y = b 1 + b 2 X 2 + b 3 X 2 + b 4 X 2 X 3* = X 22 X 4* = X 2 X 3 queda Ejemplo 2: transformando queda Y = b 1 + b 2 X 2 + b 3 X 3 + b 4 X 4 * Y = b 1 + X * 2 = b * 2 X + b 3 1 X + b 3 Y = b 1 + b 2 X * 2 Sin embargo, X 2* no se puede calcular porque no se conoce.

Aplicaciones: 1. Funcion de Producion Cobbu 3 2 Douglas: = b Y L K e 1 Transformando: ==> d ln Y = 2 d ln. L d ln Y = 3 d ln. K ln Y = ln b 1 + b 2 ln L + b 3 ln K + u ln Y = b 1 + b 2 ln L + b 3 ln K + u : elasticidad del output c. r al trabajo : elasticidad del output c. r al capital 2 + 3 => 1 Informacion sobre los rendimientos de escala <

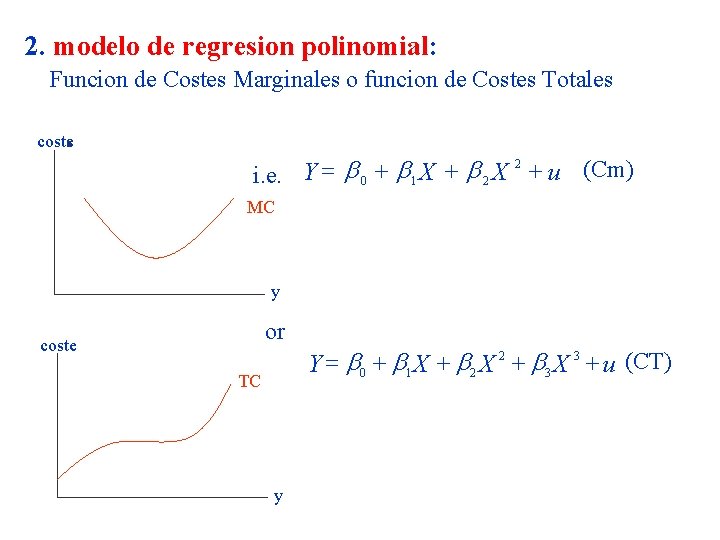
2. modelo de regresion polinomial: Funcion de Costes Marginales o funcion de Costes Totales coste 2 = b + b + u (Cm) i. e. Y 0 1 X 2 X MC y or coste TC y 2 3 = b + b + u (CT) Y 0 1 X 2 X 3 X

Pendiente Resumen d. Y (= ) d. X Del modelo lineal d. Y = 2 d. X Y = b 1 + b 2 X Log-log ln Y = b 1 + b 2 ln X d. Y d ln Y = b 2 d ln X d. X X ==> d. Y Y = b 2( ) d. X X Elasticidad d. Y (= Y ) d. X X X 2( ) Y b 2

Pendiente Resumen(Cont. ) Log-lineal ln Y = b 1 + b 2 X d. Y d ln Y = b 2 d. X d. Y = b 2 Y d. X d. Y = Lineal-log Y = b 1 + b 2 ln X d. X = b 2 X d. Y 1 = b ==> 2 d. X X d. Y 1 = = b 2 Reciproca Y = b 1 + b 2 1 1 d ( 2 ) d. X X Elasticidad b 2 X ==> d. Y -1 = b 2 d. X X 2 b 2 1 Y b 2 ( -1 ) XY

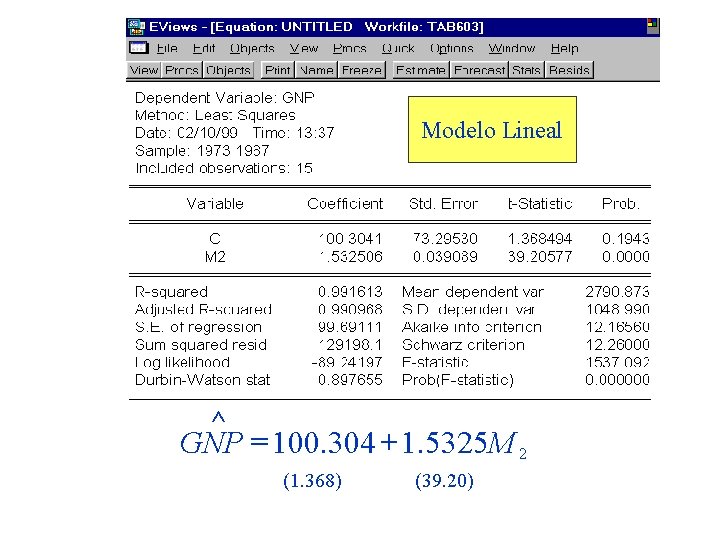
Modelo Lineal ^ GNP = 100. 304 + 1. 5325 M 2 (1. 368) (39. 20)

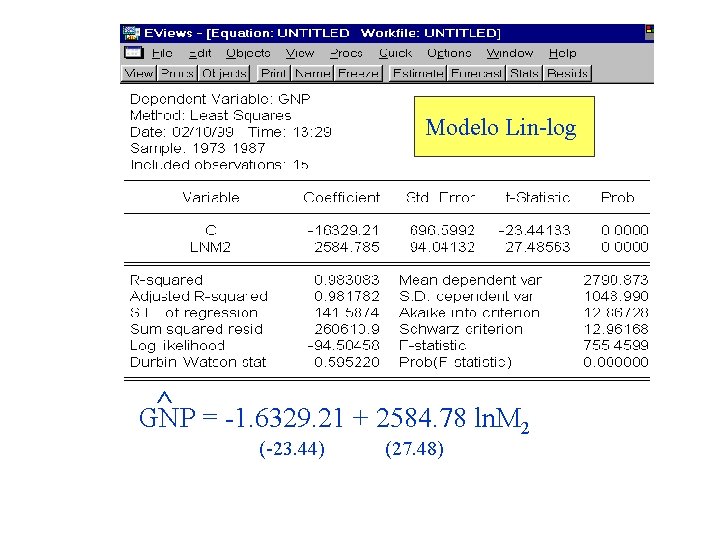
Modelo Lin-log ^ = -1. 6329. 21 + 2584. 78 ln. M GNP 2 (-23. 44) (27. 48)

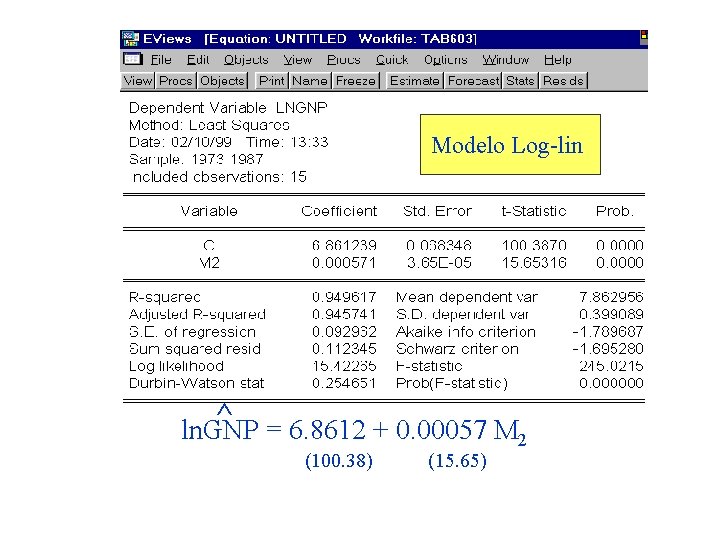
Modelo Log-lin ^ = 6. 8612 + 0. 00057 M ln. GNP 2 (100. 38) (15. 65)

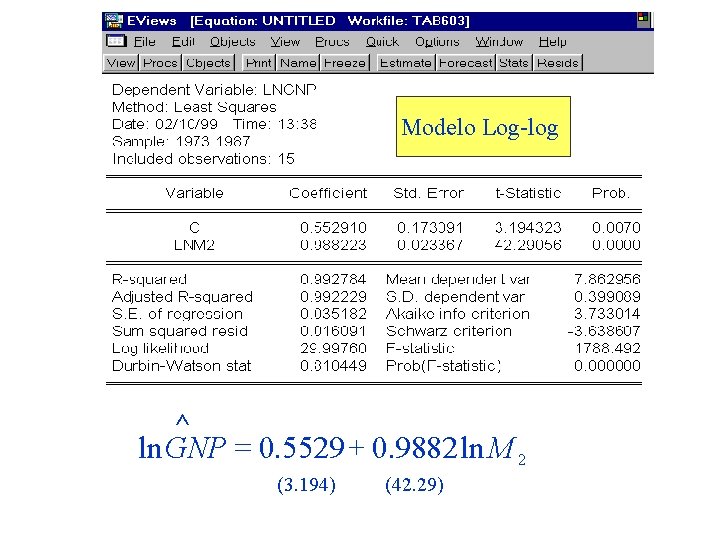
Modelo Log-log ^ ln GNP = 0. 5529 + 0. 9882 ln M 2 (3. 194) (42. 29)

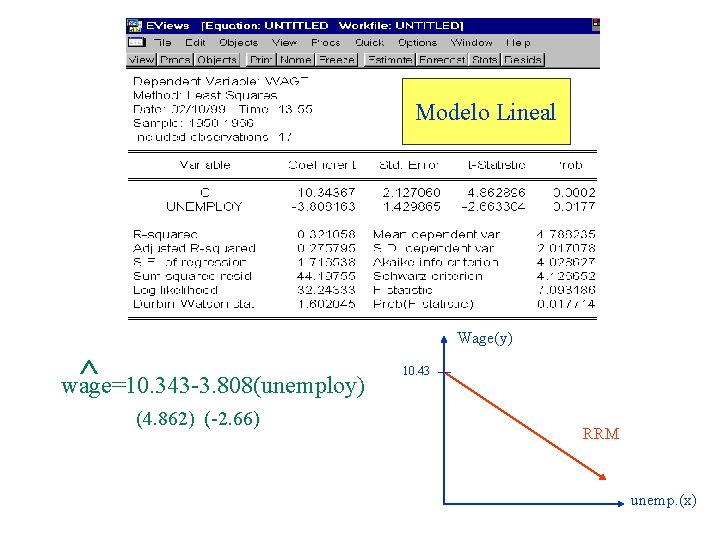
Modelo Lineal Wage(y) ^ wage=10. 343 -3. 808(unemploy) (4. 862) (-2. 66) 10. 43 RRM unemp. (x)

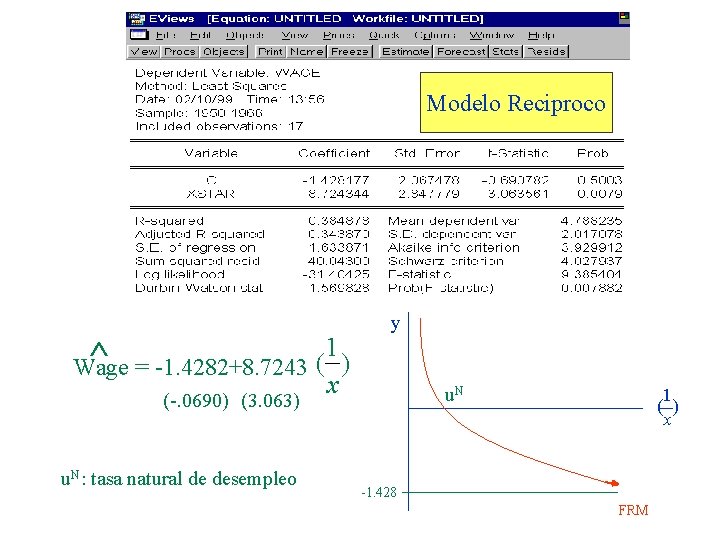
Modelo Reciproco 1 ^ Wage = -1. 4282+8. 7243 ( ) (-. 0690) (3. 063) u. N: tasa natural de desempleo y x u. N 1 ( ) x -1. 428 FRM

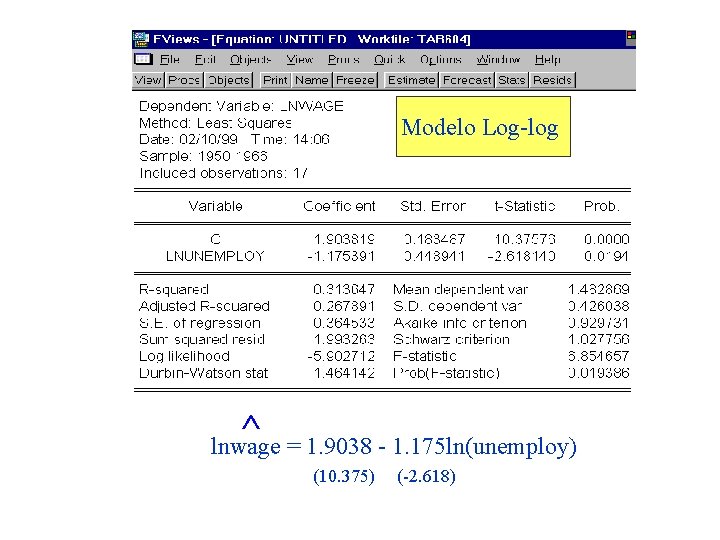
Modelo Log-log ^ lnwage = 1. 9038 - 1. 175 ln(unemploy) (10. 375) (-2. 618)

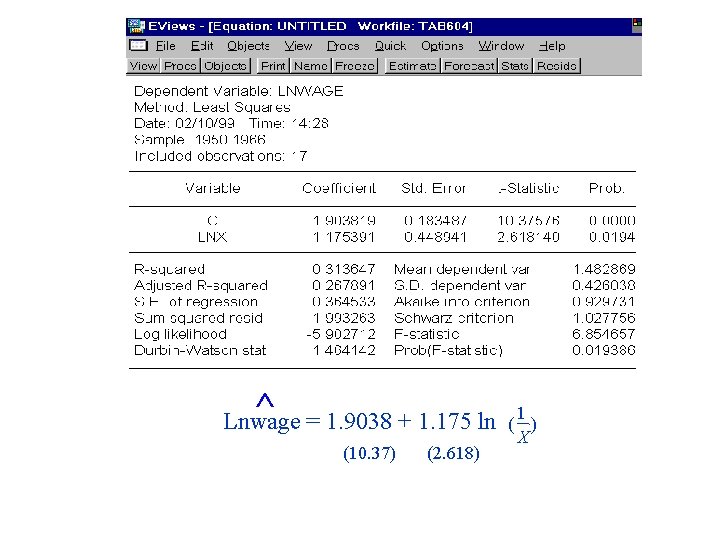
^ Lnwage = 1. 9038 + 1. 175 ln (10. 37) (2. 618) 1 ( ) X

Escala y unidades de medida Y = 1 + 2 X + ui 2 : pendiente de la recta de regresion 2 = si Y d. Y o X d. X Y* = 1000 Y X* = 1000 X entonces ==> 1000 Y = 1000 1 + 1000 2 X + 1000 u i * * * Y = *1 + *2 X + u

Cambios en la escala de X e Y Cambia el R 2? , cambian los coefficientes? Yi = 1 + 2 Xi + ui Yi/k = ( 1/k)+ 2 Xi/k + ui/k * * + u* = + X i 1 2 i i Y* donde Y*i = Yi/k u*i = ui/k *1 = 1/k y X*i = Xi/k

Cambio de escala de x Cambia el R 2? , Cambian los coeficientes? Yi = 1 + 2 Xi + ui Yi = 1 + (k 2)(Xi/k) + ui Yi = 1 + * * +u X 2 i i donde * = 2 k 2 y X*i = Xi/k

Cambio de escala de Y Yi = 1 + 2 Xi + ui Yi/k = ( 1/k) + ( 2/k)Xi + ui/k Cambia el R 2? , cambian los coeficientes? Y* * donde Y*i = Yi/k u*i = ui/k i = 1 + *1 = 1/k * *u X + 2 i i y *2 = 2/k