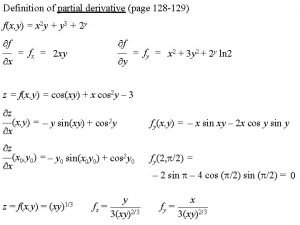Definition of partial derivative page 128 129 fx
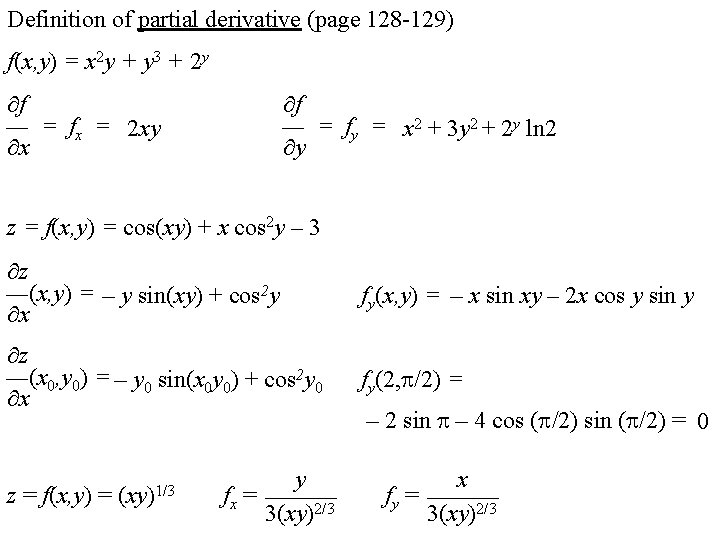








- Slides: 11
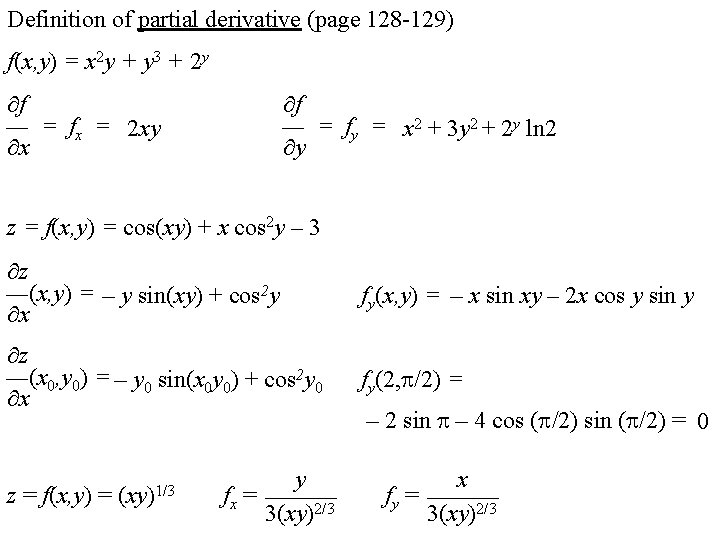
Definition of partial derivative (page 128 -129) f(x, y) = x 2 y + y 3 + 2 y f — = fx = 2 xy x f — = fy = x 2 + 3 y 2 + 2 y ln 2 y z = f(x, y) = cos(xy) + x cos 2 y – 3 z —(x, y) = – y sin(xy) + cos 2 y x fy(x, y) = – x sin xy – 2 x cos y sin y z —(x 0, y 0) = – y 0 sin(x 0 y 0) + cos 2 y 0 x fy(2, /2) = z = f(x, y) = (xy)1/3 y fx = ——— 3(xy)2/3 – 2 sin – 4 cos ( /2) sin ( /2) = 0 x fy = ——— 3(xy)2/3

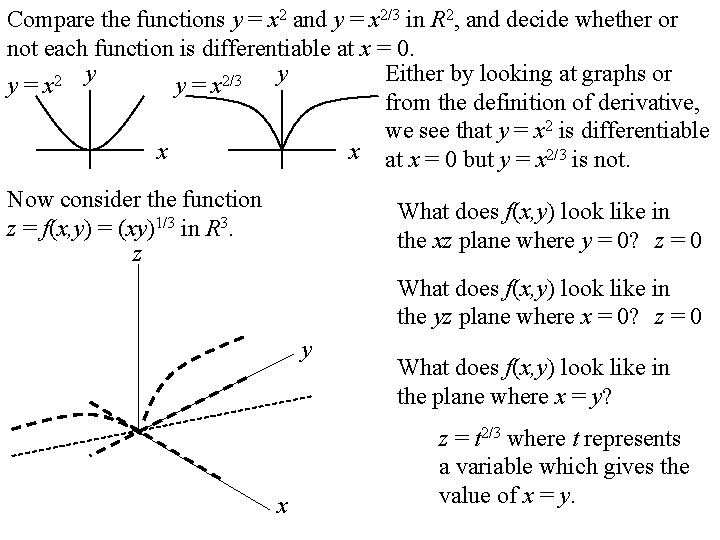
Compare the functions y = x 2 and y = x 2/3 in R 2, and decide whether or not each function is differentiable at x = 0. Either by looking at graphs or y = x 2 y y = x 2/3 y from the definition of derivative, we see that y = x 2 is differentiable x x at x = 0 but y = x 2/3 is not. Now consider the function z = f(x, y) = (xy)1/3 in R 3. z What does f(x, y) look like in the xz plane where y = 0? z = 0 What does f(x, y) look like in the yz plane where x = 0? z = 0 y x What does f(x, y) look like in the plane where x = y? z = t 2/3 where t represents a variable which gives the value of x = y.

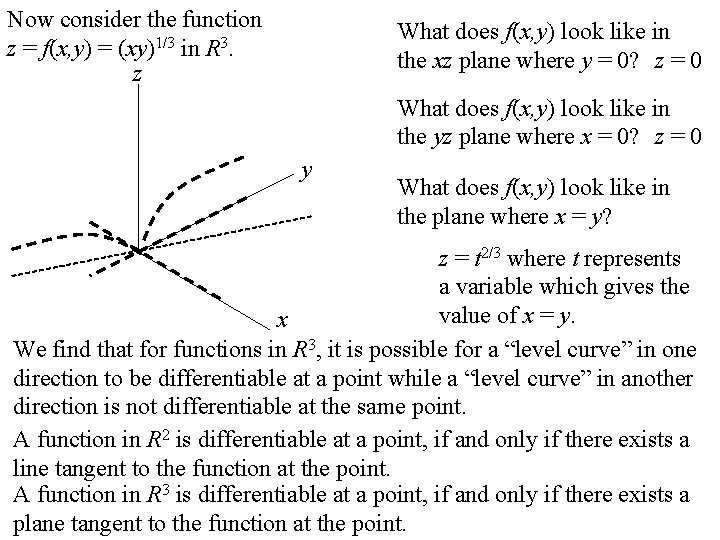
Now consider the function z = f(x, y) = (xy)1/3 in R 3. z What does f(x, y) look like in the xz plane where y = 0? z = 0 What does f(x, y) look like in the yz plane where x = 0? z = 0 y What does f(x, y) look like in the plane where x = y? z = t 2/3 where t represents a variable which gives the value of x = y. x We find that for functions in R 3, it is possible for a “level curve” in one direction to be differentiable at a point while a “level curve” in another direction is not differentiable at the same point. A function in R 2 is differentiable at a point, if and only if there exists a line tangent to the function at the point. A function in R 3 is differentiable at a point, if and only if there exists a plane tangent to the function at the point.

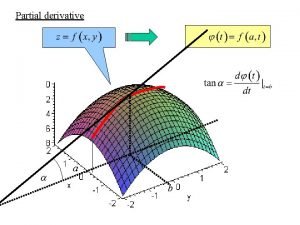
In order that a function f(x, y) be differentiable at a point (x 0 , y 0), the function must be “smooth” in all directions, not just in the x-direction and y-direction. If a function f(x, y) is differentiable at point (x 0 , y 0), then we can use the value of each partial derivative at the point to find the equation of the plane tangent to the function at the point: The equation of the tangent plane can be written as g(x, y) = ax + by + c. The following must be true: g(x 0 , y 0) = ax 0 + by 0 + c = f(x 0 , y 0) , gx(x 0 , y 0) = a = fx(x 0 , y 0) , gy(x 0 , y 0) = b = fy(x 0 , y 0). The equation of the tangent plane is g(x, y) = fx(x 0 , y 0) x + fy(x 0 , y 0) y + f(x 0 , y 0) – fx(x 0 , y 0) x 0 – fy(x 0 , y 0) y 0 which can be written z = f(x 0 , y 0) + fx(x 0 , y 0) (x – x 0) + fy(x 0 , y 0) (y – y 0).

Definition of differentiable and tangent plane in R 3 (page 133) See the derivation on page 132. Example Find the plane tangent to the graph of z = x 2 + y 3 – cos( xy) at the point (8 , – 4 , – 1). f(8 , – 4) = – 1 f — = fx = 2 x + y sin( xy) x f — = fy = 3 y 2 + x sin( xy) y fx(8 , – 4) = 16 fy(8 , – 4) = 48 The equation of the tangent plane is z = – 1 + 16(x – 8) + 48(y + 4) which can be written 16 x + 48 y – z = – 63.

Look again at the definition of differentiable in R 3 on page 133, and observe that we can say f(x, y) is differentiable at (x 0 , y 0) if This is the difference between the exact function value at point (x , y) and the approximated value from the plane tangent to the function at (x 0 , y 0). f(x, y) – f(x 0 , y 0) – fx(x 0 , y 0) fy(x 0 , y 0) (x – x 0) (y – y 0) lim ——————————— = 0 (x , y) (xo , y 0) ||(x , y) – (xo , y 0)|| If x = (x 1 , x 2 , …, xn) is a vector in Rn, and f(x) is a function from Rn to R, then we define f(x) to differentiable at x 0 if f(x) – f(x 0) – Df(x 0) (x – x 0) lim —————— = 0 where x xo || x – x 0 || Df(x 0) is the 1 n matrix of partial derivatives at x 0 , and (x – x 0) is the n 1 matrix consisting of the differences between each variable and its specific value at x 0. (NOTE: A 1 n matrix times an n 1 matrix is the same as the dot product of two vectors.

Suppose x = (x 1 , x 2 , …, xn) is a vector in Rn, and f(x) is a function from Rn to Rm. Then, we can write f(x) = [f 1(x) , f 2(x) , … , fm(x)]. We let Df(x) represent the m n matrix with row i consisting of the following partial derivatives: fi fi fi —— —— … ——. x 1 x 2 xn We call Df(x) the derivative (matrix) of f , and of course Df(x 0) is the derivative (matrix) of f at x 0. Look at the general definition of differentiable on page 134.

Example Find the derivative matrix for w = f(x, y, z) = ( x 2 + xy 4 eyz , ln(xz+y) ). _ _ | | | 2 x + y 4 eyz | 4 xy 3 eyz + xy 4 zeyz xy 5 eyz | | Df(x, y, z) = | | 1 / (xz+y) x / (xz+y) | z / (xz+y) | | |_ _| Find the linear approximation at the point x 0 = (1 , e , 0). x– 1 w = f (x 0) + Df (x 0) (x – x 0) = f (1 , e , 0) + Df (1 , e , 0) y – e z– 0 =

1+ e 4 1 1 + e 4 1 2 + e 4 4 e 3 e 5 + y–e 0 + x– 1 1/e (2 + e 4)x – 2 – e 4 + 4 e 3 y – 4 e 4 + e 5 z y/e – 1 + z/e = z– 0 = (2 + e 4)x + 4 e 3 y + e 5 z – 1 – 4 e 4 (y + z) / e Observe that since w = f(x, y, z) goes from R 3 to R 2, this linear approximation is really two linear approximations, one for each of the component functions. That is,

Observe that since w = f(x, y, z) goes from R 3 to R 2, this linear approximation is really two linear approximations, one for each of the component functions. That is, The linear approximation for f 1(x, y, z) = x 2 + xy 4 eyz is w 1 = (2 + e 4)x + 4 e 3 y + e 5 z– (1 + 4 e 4). The linear approximation for f 2(x, y, z) = ln(xz+y) is w 2 = (1/e)y + (1/e)z.

Recall that for a function f from Rn to R 1, the derivative matrix is 1 n. In certain situations, it will be convenient to treat this 1 n matrix as a vector. See the definition of a gradient on page 136. Look at Theorem 8 on page 137. Look at Theorem 9 on page 137. Look at the chart at the top of page 138.
 The elevator incident by melinda
The elevator incident by melinda Definition of partial derivative
Definition of partial derivative Definition of partial derivative
Definition of partial derivative Second order partial derivatives examples
Second order partial derivatives examples Partial derivative tree
Partial derivative tree Partial differentiation
Partial differentiation Partial differentiation
Partial differentiation 편미분 예제
편미분 예제 Van der waals equation partial derivative
Van der waals equation partial derivative Amaranto colorante artificial
Amaranto colorante artificial Ecs 129 uc davis
Ecs 129 uc davis Taskj-129
Taskj-129