Data Parallel Computations and Pattern ITCS 45145 Parallel










- Slides: 14

Data Parallel Computations and Pattern ITCS 4/5145 Parallel computing, UNC-Charlotte, B. Wilkinson, slides 6 c. ppt Nov 4, 2013 6 c. 1

Data Parallel Computations Same operation performed on different data elements simultaneously; i. e. , in parallel, fully synchronous. Particularly convenient because: • Can scale easily to larger problem sizes. • Many numeric and some non-numeric problems can be cast in a data parallel form. • Ease of programming (only one program!). 6 c. 2

Single Instruction Multiple Data (SIMD) model Data parallel model used in vector super-computers designs in 1970 s: • • Synchronism at the instruction level. Each instruction specifies a “vector” operation and elements of array to perform operation on. Multiple execution units, each executes operation on a different element or pairs of elements in synchronism Only one instruction fetch/decode unit Subsequently seen in Intel processors -- Vector SSE (Streaming SIMD Extensions) instructions. 6 c. 3

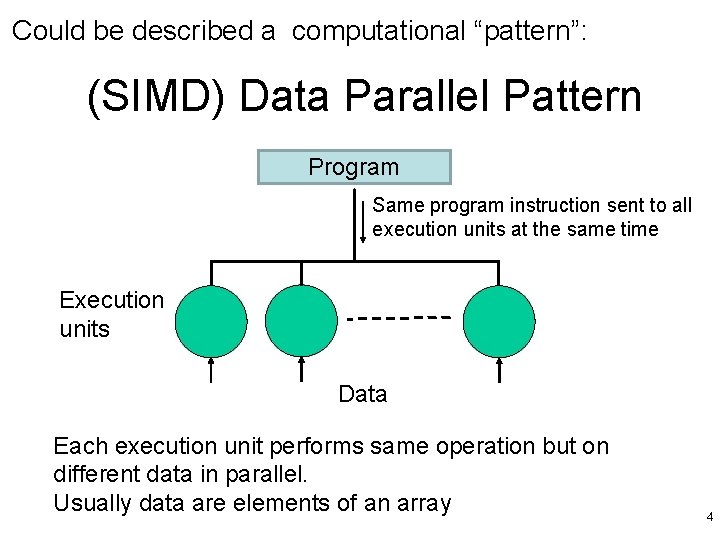
Could be described a computational “pattern”: (SIMD) Data Parallel Pattern Program Same program instruction sent to all execution units at the same time Execution units Data Each execution unit performs same operation but on different data in parallel. Usually data are elements of an array 4

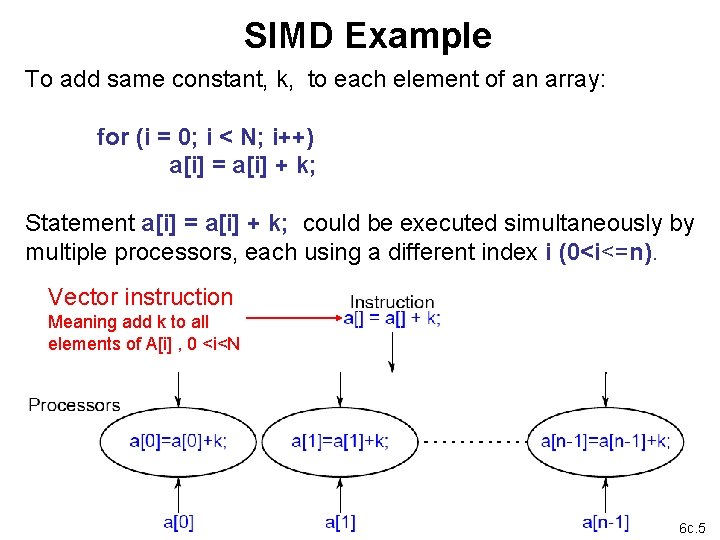
SIMD Example To add same constant, k, to each element of an array: for (i = 0; i < N; i++) a[i] = a[i] + k; Statement a[i] = a[i] + k; could be executed simultaneously by multiple processors, each using a different index i (0<i<=n). Vector instruction Meaning add k to all elements of A[i] , 0 <i<N 6 c. 5

Using forall construct for data parallel pattern Could use forall to specify data parallel operations forall (i = 0; i < n; i++) a[i] = a[i] + k However, forall is more general – it states that the n instances of the body can be executed simultaneously or in any order (not necessarily executed at the same time). We shall see this in GPU implementation of data parallel pattern. Note forall does imply synchronism at its end – all instances must complete before continuing, which will be true in GPUs 6. 6

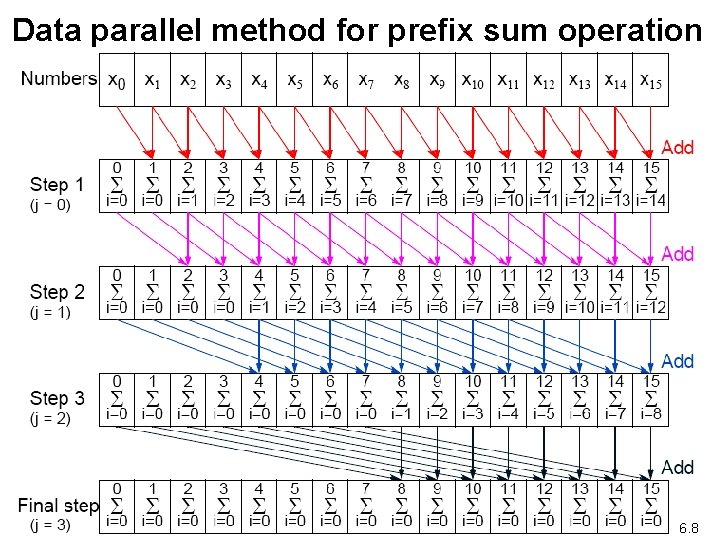
Data Parallel Example Prefix Sum Problem Given a list of numbers, x 0, …, xn-1, compute all the partial summations, i. e. : x 0 + x 1; x 0 + x 1 + x 2 + x 3; x 0 + x 1 + x 2 + x 3 + x 4; … Can also be defined with associative operations other than addition. Widely studied. Practical applications in areas such as processor allocation, data compaction, sorting, and polynomial evaluation. 6. 7

Data parallel method for prefix sum operation 6. 8

Sequential pseudo code for (j = 0; j < log(n); j++) j for (i = 2 ; i < n; i++) // at each step // accumulate sum x[i] = x[i] + x[i + 2 j]; Parallel code using forall notation for (j = 0; j < log(n); j++) forall (i = 0; i < n; i++) // at each step // accumulate sum 6 c. 9

Low level image processing Involves manipulating image pixels (picture elements) and often the same operation on each pixel using neighboring pixel values SIMD (single instruction multiple data) model very applicable. Historically, GPUs designed for creating image data for displays using this model. 10

Single Instruction Multiple Thread Programming Model (SIMT) A version of SIMD used in recent GPUs use a thread model to achieve very high parallel performance and to hide memory latency Multiple threads, each execute the same instruction sequence. A very large number of threads (10, 000’s) can be declared in the program. Our GPUs have 448 and 2496 cores on each chip (see later), providing that number of simultaneous threads. Groups of threads scheduled to execute at the same time on execution cores. Very low thread overhead. 11

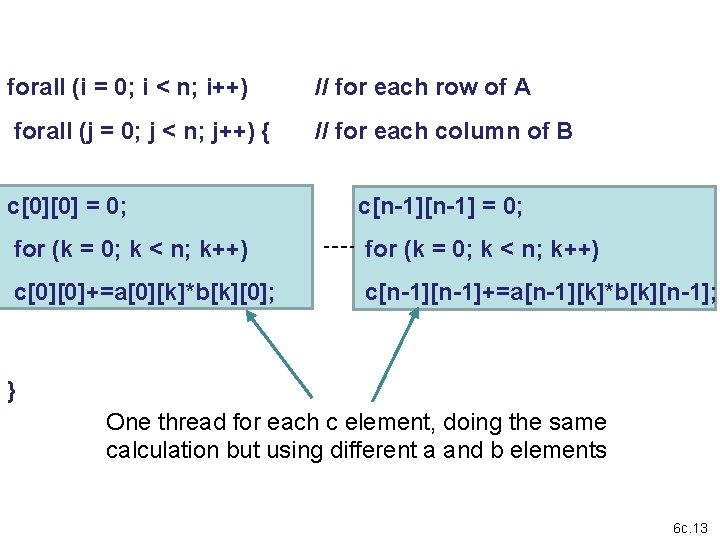
SIMT Example -- Matrix Multiplication Matrix multiplication easy to make a data parallel version. Change two for’s to forall’s: forall (i = 0; i < n; i++) // for each row of A forall (j = 0; j < n; j++) { // for each column of B c[i][j] = 0; for (k = 0; k < n; k++) c[i][j] += a[i][k] * b[k][j]; } Each instance of body is a separate thread, doing same 6 c. 12

forall (i = 0; i < n; i++) // for each row of A forall (j = 0; j < n; j++) { // for each column of B c[0][0] = 0; c[n-1] = 0; for (k = 0; k < n; k++) c[0][0]+=a[0][k]*b[k][0]; c[n-1]+=a[n-1][k]*b[k][n-1]; } One thread for each c element, doing the same calculation but using different a and b elements 6 c. 13

We will explore programming GPUs for high performance computing next. Questions so far 6. 14