Pipeline Pattern ITCS 45145 Parallel Computing UNCCharlotte B

Pipeline Pattern ITCS 4/5145 Parallel Computing, UNC-Charlotte, B. Wilkinson, 2012 slides 5. ppt March 20, 2014. 5. 1
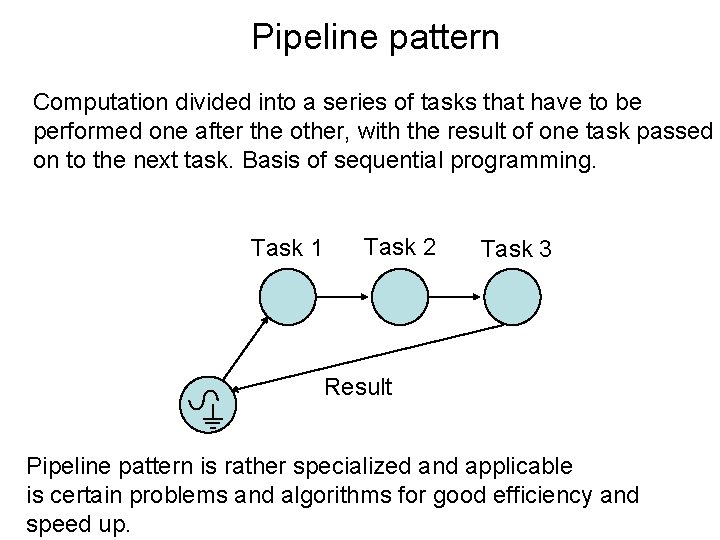
Pipeline pattern Computation divided into a series of tasks that have to be performed one after the other, with the result of one task passed on to the next task. Basis of sequential programming. Task 1 Task 2 Task 3 Result Pipeline pattern is rather specialized and applicable is certain problems and algorithms for good efficiency and speed up.
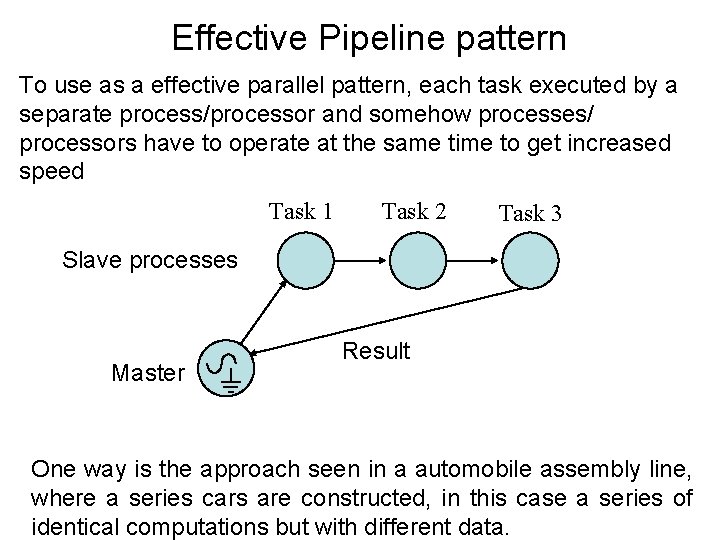
Effective Pipeline pattern To use as a effective parallel pattern, each task executed by a separate process/processor and somehow processes/ processors have to operate at the same time to get increased speed Task 1 Task 2 Task 3 Slave processes Master Result One way is the approach seen in a automobile assembly line, where a series cars are constructed, in this case a series of identical computations but with different data.

Seeds Pipeline Pattern See “Pipeline Template Tutorial. ” by Jeremy Villalobos. http: //coit-grid 01. uncc. edu/seeds/docs/pipeline_tutorial. pdf Interface: public abstract class Pipe. Line extends Basic. Layer. Interface { public abstract Data Compute(int stage, Data input); public abstract Data Diffuse. Data(int segment); public abstract void Gather. Data(int segment, Data dat); public abstract int get. Data. Count(); public abstract int get. Stage. Count(); } 5. 4

Pipeline applications Broadly speaking, we can divide pipeline applications into two types: 1. More than one instance of complete problem is executed. Partial results passes from one pipeline stage to the next – example is an automobile assembly line building cars. 2. A single problem instance is executed that has a series of data items to be processed sequentially, each requiring multiple operations. Numbers pass from one stage to the next Although a pipeline application may exhibit features of both types. Sometimes a single problem instance requires a series of data items to be processed 5. 5

1. More than one instance of the complete problem is to be executed Pipeline Space-Time Diagram p stages m instances of problem Execution time = p + m – 1 steps 5. 6

Speedup factor So if we provide a constant stream of instances of the problem, get maximum speedup.

2. Single problem with a series of data items to be processed Pipeline Space-Time Diagram n data items Execution time = p + n – 1 steps 5. 8

Speedup factor So if we provide a constant stream of data items, get maximum speedup. Processors can use this form of pipeline for streams of data (video etc. )

Single problem with a series of data items to be processed Examples

Sorting numbers with a pipeline pattern Parallel version of Insertion sort: Each number is inserted into the position such that all numbers before it are smaller, by comparing with all the numbers before it. 1 2 3 4 Time steps 5 6 Numbers to sort 4, 3, 1, 2, 5 4, 3, 1, 2 5 4, 3, 1 2 4, 3 4 1 1 1 7 1 8 1 5 2 3 4 5 2 2 5 3 4 5 3 3 5 4 5 9 1 2 3 4 10 1 2 3 4 5 5
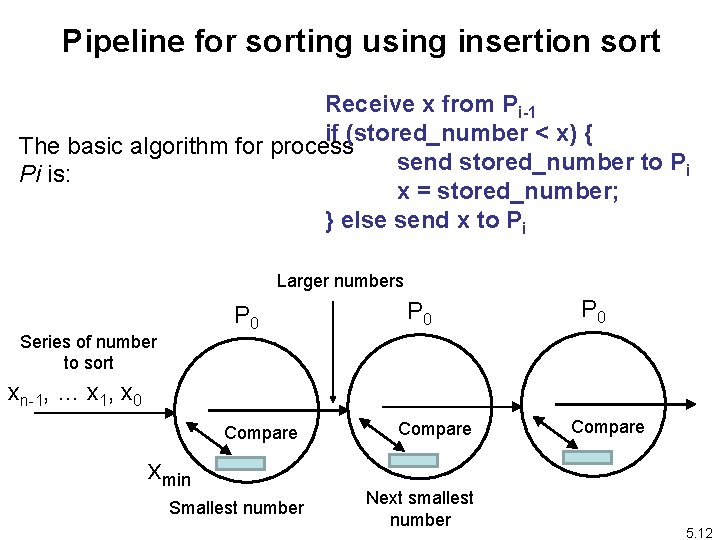
Pipeline for sorting using insertion sort Receive x from Pi-1 if (stored_number < x) { The basic algorithm for process send stored_number to Pi Pi is: x = stored_number; } else send x to Pi Larger numbers P 0 Series of number to sort P 0 xn-1, … x 1, x 0 Compare xmin Smallest number Compare Next smallest number Compare 5. 12
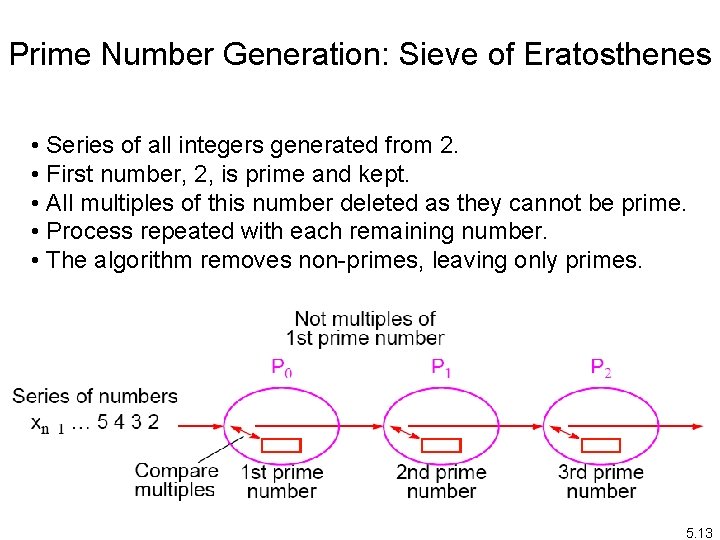
Prime Number Generation: Sieve of Eratosthenes • Series of all integers generated from 2. • First number, 2, is prime and kept. • All multiples of this number deleted as they cannot be prime. • Process repeated with each remaining number. • The algorithm removes non-primes, leaving only primes. 5. 13
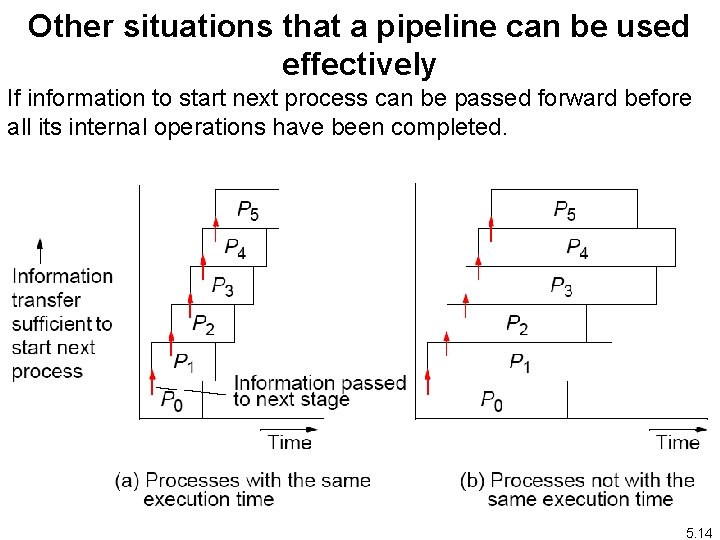
Other situations that a pipeline can be used effectively If information to start next process can be passed forward before all its internal operations have been completed. 5. 14

Example: Solving Upper-triangular System of Linear Equations using Back Substitution (created after Gaussian Elimination step for a general system of linear equations) a’s and b’s are constants and x’s are unknowns to be found. 5. 15

Back Substitution First, unknown x 0 is found from last equation; i. e. , Value obtained for x 0 substituted into next equation to obtain x 1; i. e. , Values obtained for x 1 and x 0 substituted into next equation to obtain x 2: and so on until all the unknowns are found. 5. 16
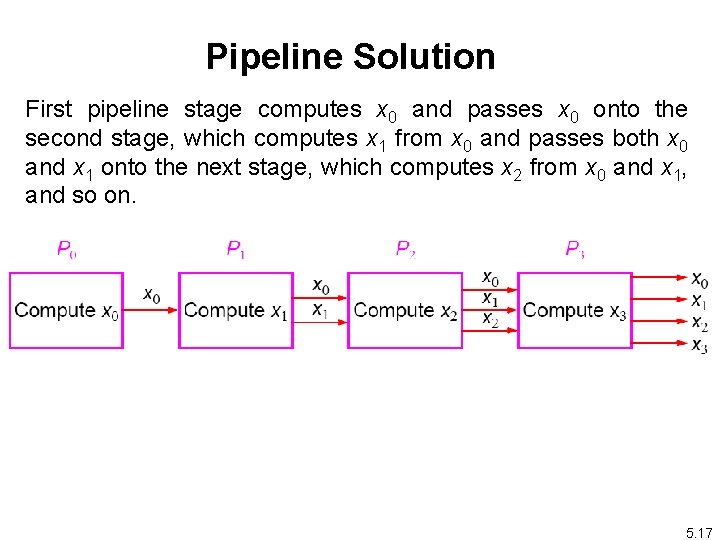
Pipeline Solution First pipeline stage computes x 0 and passes x 0 onto the second stage, which computes x 1 from x 0 and passes both x 0 and x 1 onto the next stage, which computes x 2 from x 0 and x 1, and so on. 5. 17
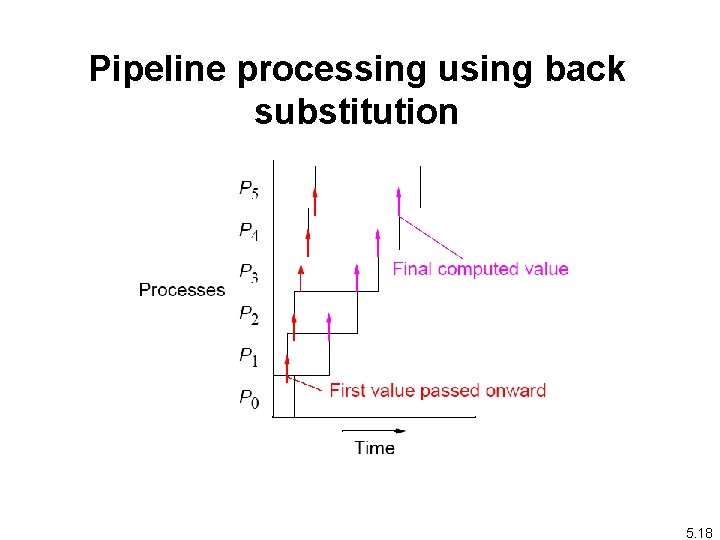
Pipeline processing using back substitution 5. 18

More complex pipelines • Two dimensional • Multifunction, multiple paths, feedback and feedforward paths, multiple outputs -- these types of pipelines are found in logic design courses
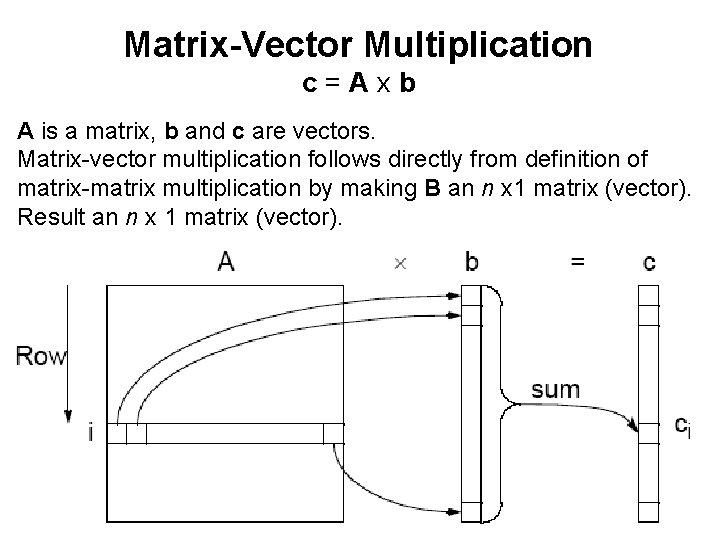
Matrix-Vector Multiplication c = A x b A is a matrix, b and c are vectors. Matrix-vector multiplication follows directly from definition of matrix-matrix multiplication by making B an n x 1 matrix (vector). Result an n x 1 matrix (vector). 20
![Matrix-Vector Multiplication B[3] B[2] B[1] B[0] A[0][3] A[0][2] A[0][1] A[0][0]. . a a a Matrix-Vector Multiplication B[3] B[2] B[1] B[0] A[0][3] A[0][2] A[0][1] A[0][0]. . a a a](http://slidetodoc.com/presentation_image/8da681c52a94226ff47bbc1723ae7922/image-21.jpg)
Matrix-Vector Multiplication B[3] B[2] B[1] B[0] A[0][3] A[0][2] A[0][1] A[0][0]. . a a a sin sout sin a sout P 0 P 1 P 2 C[0] C[1] C[2] B array elements pass through A[0][3] A[0][2] A[0][1] A[0][0]. . . delay sin sout P 3 C[3] C elements accumulate in pipeline stages
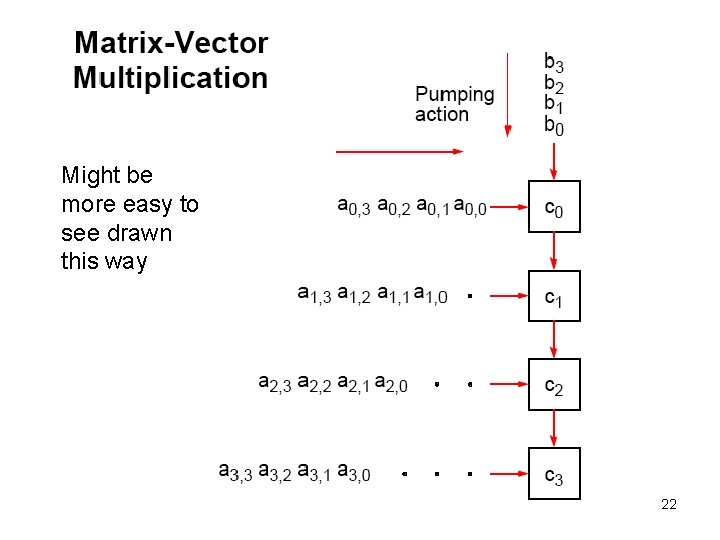
Might be more easy to see drawn this way 22
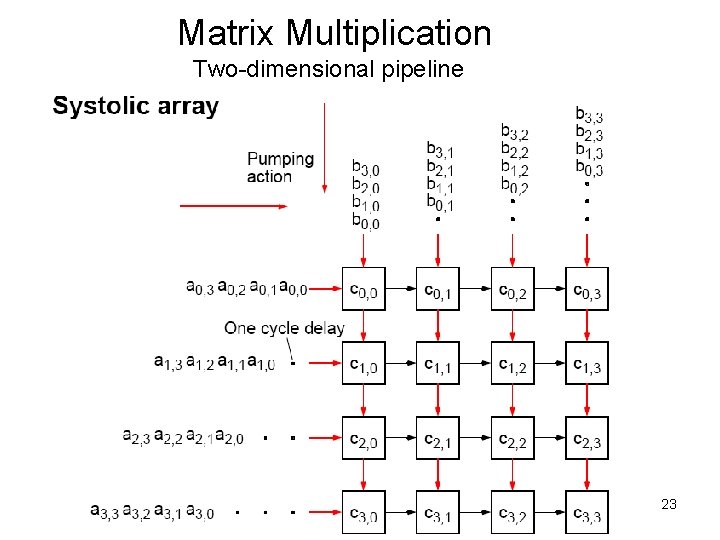
Matrix Multiplication Two-dimensional pipeline 23
Example pipeline with two paths This is an application for a pattern operator
Structures that allow two-way movement between stages Not truly a pipeline We will look into these structures separately.

Questions 5. 26
- Slides: 26