CS 3343 Analysis of Algorithms Quick sort and








![Partition Code Partition(A, p, r) x = A[p]; // pivot is the first element Partition Code Partition(A, p, r) x = A[p]; // pivot is the first element](https://slidetodoc.com/presentation_image_h/30526be8a686e7fac319d96d5d53bfdf/image-10.jpg)


















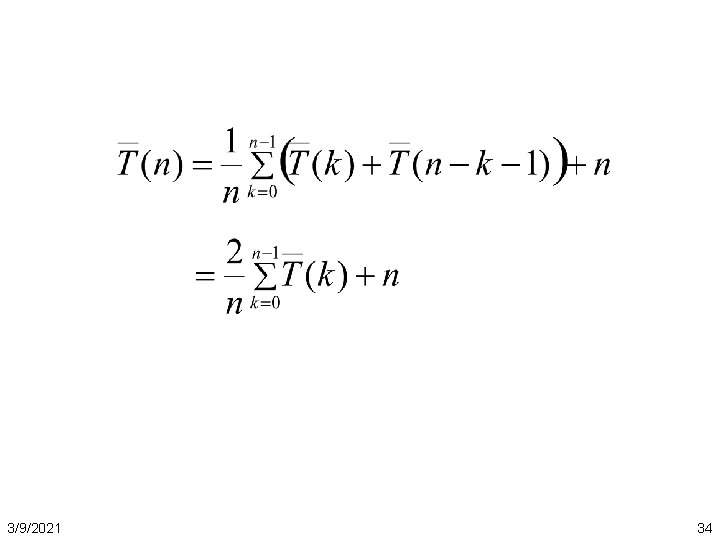









- Slides: 43

CS 3343: Analysis of Algorithms Quick sort and average-case running time analysis 3/9/2021 1

Quick sort • Another divide and conquer sorting algorithm – like merge sort • Anyone remember the basic idea? • The worst-case and average-case running time? • Learn some new algorithm analysis tricks 3/9/2021 2

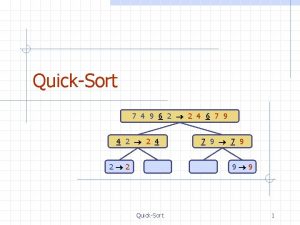
Quick sort Quicksort an n-element array: 1. Divide: Partition the array into two subarrays around a pivot x such that elements in lower subarray x elements in upper subarray. x x ≥x 2. Conquer: Recursively sort the two subarrays. 3. Combine: Trivial. Key: Linear-time partitioning subroutine. 3/9/2021 3

Partition • All the action takes place in the partition() function – Rearranges the subarray in place – End result: two subarrays • All values in first subarray all values in second – Returns the index of the “pivot” element separating the two subarrays p x 3/9/2021 r q x ≥x 4

Pseudocode for quicksort QUICKSORT(A, p, r) if p < r then q PARTITION(A, p, r) QUICKSORT(A, p, q– 1) QUICKSORT(A, q+1, r) Initial call: QUICKSORT(A, 1, n) 3/9/2021 5

Idea of partition • If we are allowed to use a second array, it would be easy 3/9/2021 6 10 5 8 13 3 2 11 6 5 3 2 11 13 8 10 2 5 3 6 11 13 8 10 6

Another idea • Keep two iterators: one from head, one from tail 3/9/2021 6 10 5 8 13 3 2 11 6 2 5 3 13 8 10 11 3 2 5 6 13 8 10 11 7

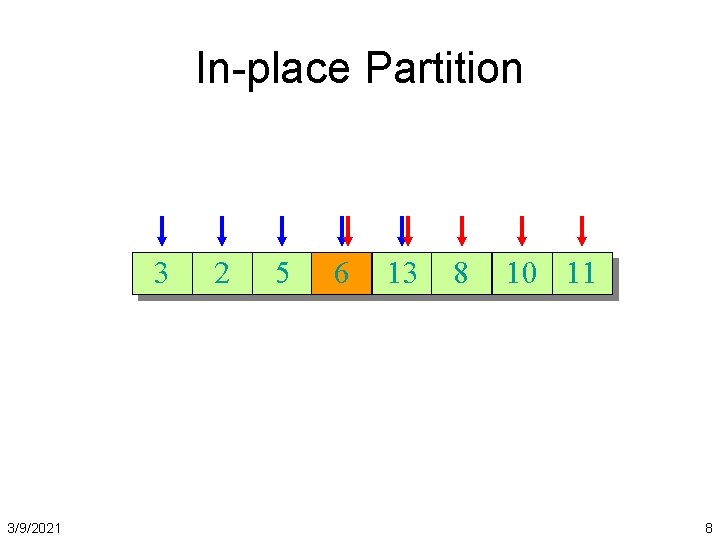
In-place Partition 36 3/9/2021 10 2 5 638 13 83 2 11 10 8

Partition In Words • Partition(A, p, r): – Select an element to act as the “pivot” (which? ) – Grow two regions, A[p. . i] and A[j. . r] • All elements in A[p. . i] <= pivot • All elements in A[j. . r] >= pivot – – – 3/9/2021 Increment i until A[i] > pivot Decrement j until A[j] < pivot Swap A[i] and A[j] Note: different from book’s Repeat until i >= j partition(), which uses two Swap A[j] and A[p] iterators that both move forward. Return j 9
![Partition Code PartitionA p r x Ap pivot is the first element Partition Code Partition(A, p, r) x = A[p]; // pivot is the first element](https://slidetodoc.com/presentation_image_h/30526be8a686e7fac319d96d5d53bfdf/image-10.jpg)
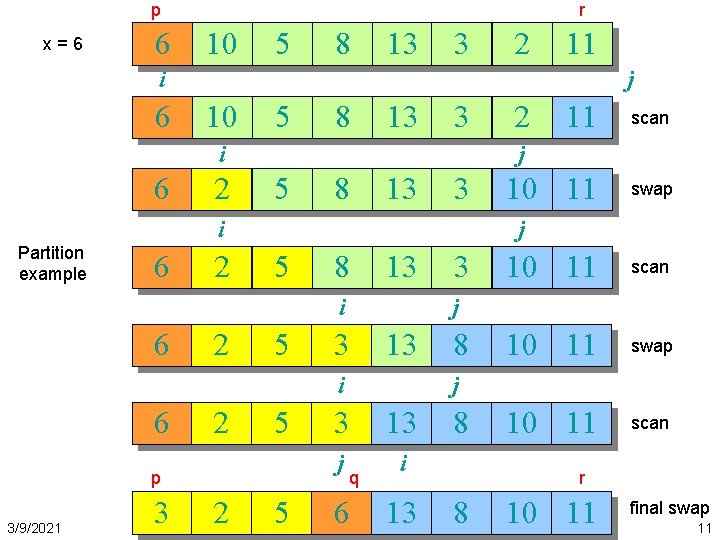
Partition Code Partition(A, p, r) x = A[p]; // pivot is the first element i = p; j = r + 1; while (TRUE) { repeat i++; until A[i] > x or i >= j; repeat What is the running time of j--; until A[j] < x or j < i; partition()? if (i < j) Swap (A[i], A[j]); else break; partition() runs in (n) time } swap (A[p], A[j]); return j; 3/9/2021 10

p x=6 6 r 10 5 8 13 3 2 11 i 6 j 10 5 8 13 3 i 6 2 5 8 13 3 2 5 5 p 3/9/2021 3 2 10 11 swap 5 3 10 11 scan 10 11 swap 10 11 scan j 3 13 i 6 scan j i 6 11 j i Partition example 2 8 j 3 13 j i q 6 13 8 r 8 10 11 final swap 11

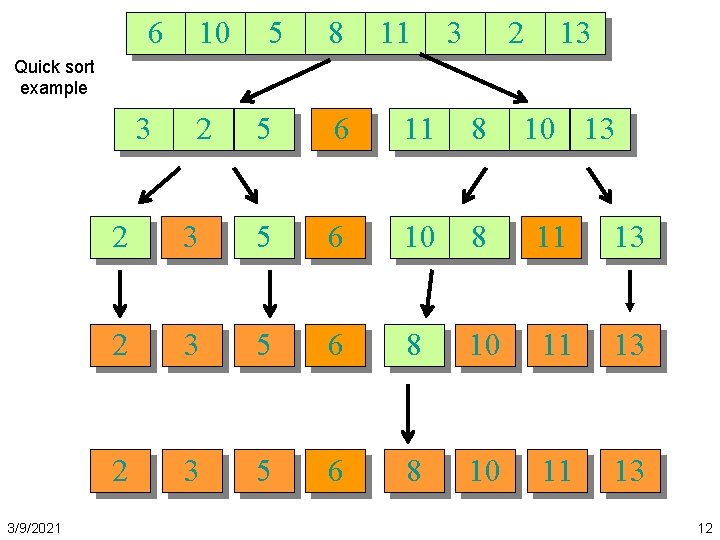
6 10 5 8 11 3 2 13 Quick sort example 3 3/9/2021 2 5 6 11 8 10 13 2 3 5 6 10 8 11 13 2 3 5 6 8 10 11 13 12

Analysis of quicksort • Assume all input elements are distinct. • In practice, there are better partitioning algorithms for when duplicate input elements may exist. • Let T(n) = worst-case running time on an array of n elements. 3/9/2021 13

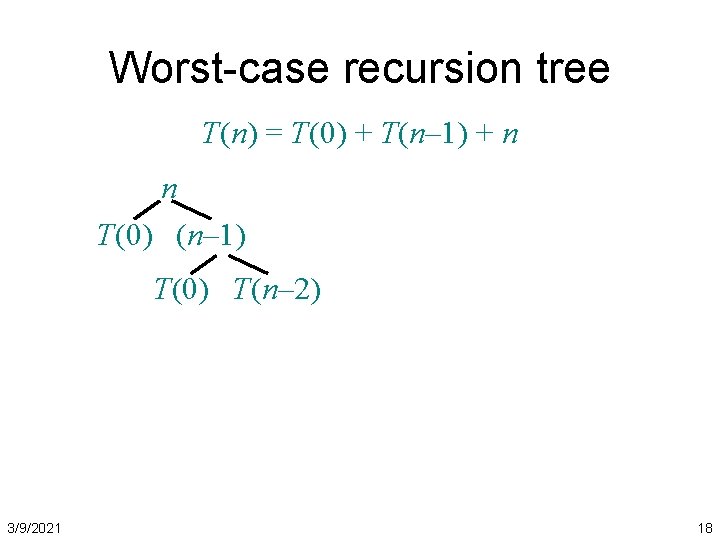
Worst-case of quicksort • Input sorted or reverse sorted. • Partition around min or max element. • One side of partition always has no elements. (arithmetic series) 3/9/2021 14

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n 3/9/2021 15

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n T(n) 3/9/2021 16

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) T(n– 1) 3/9/2021 17

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) (n– 1) T(0) T(n– 2) 3/9/2021 18

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) (n– 1) T(0) (n– 2) T(0) 3/9/2021 19

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) (n– 1) height = n height T(0) (n– 2) T(0) 3/9/2021 20

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) (n– 1) height = n n T(0) (n– 2) T(0) 3/9/2021 21

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n (1) (n– 2) height = n (1) n T(n) = (n) + (n 2) = (n 2) (1) 3/9/2021 22

Best-case analysis (For intuition only!) If we’re lucky, PARTITION splits the array evenly: T(n) = 2 T(n/2) + (n) = (n log n) (same as merge sort) What if the split is always ? What is the solution to this recurrence? 3/9/2021 23

Analysis of “almost-best” case 3/9/2021 24

Analysis of “almost-best” case n 3/9/2021 25

Analysis of “almost-best” case n 3/9/2021 26

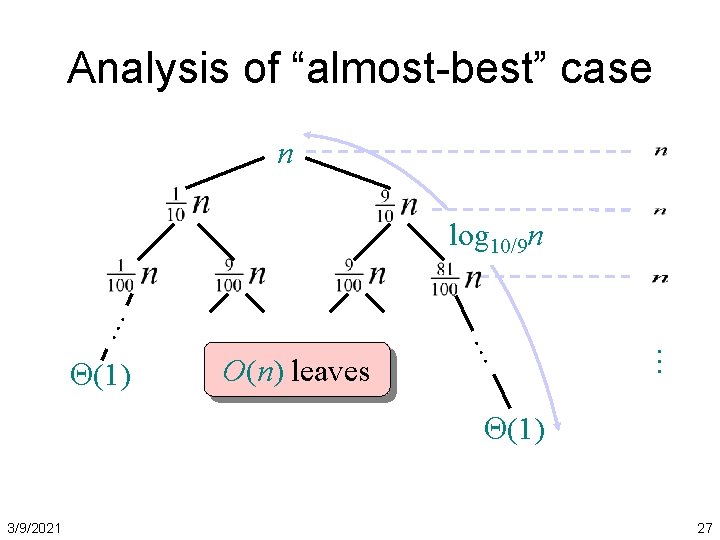
Analysis of “almost-best” case n O(n) leaves … (1) … … log 10/9 n (1) 3/9/2021 27

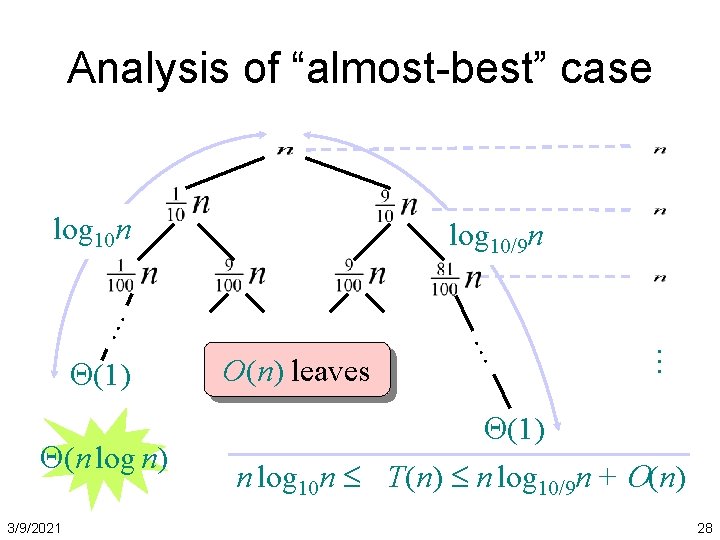
Analysis of “almost-best” case log 10 n (n log n) 3/9/2021 O(n) leaves … (1) … … log 10/9 n (1) n log 10 n T(n) n log 10/9 n + O(n) 28

Quicksort Runtimes • Best-case runtime Tbest(n) (n log n) • Worst-case runtime Tworst(n) (n 2) • Worse than mergesort? Why is it called quicksort then? • Its average runtime Tavg(n) (n log n ) • Better even, the expected runtime of randomized quicksort is (n log n) 3/9/2021 29

Expected running time Alg (n) r = rand(); // r is a random number between 0 and 1; if (r <= 0. 5) Alg (n/2); else Alg (n/2); end • Best case? • Worst case? • Average Case? 3/9/2021 • T(n) = T(n/2) + 1 Θ (log n) • T(n) = 2 T(n/2) + 1 Θ (n) • T(n) = 0. 5 (T(n/2) + 1) + 0. 5 (2 T(n/2) + 1) = 1. 5 T(n/2) + 1 Θ (nlog 21. 5) 30

Expected running time (ex. 2) Alg (n) r = rand(); // r is a random number between 0 and 1; if (r <= 0. 1) Alg (n/2); else Alg (n/2); end • Best case? • Worst case? • Average Case? 3/9/2021 • T(n) = T(n/2) + 1 Θ (log n) • T(n) = 2 T(n/2) + 1 Θ (n) • T(n) = 0. 1 (T(n/2) + 1) + 0. 9 (2 T(n/2) + 1) = 1. 9 T(n/2) + 1 Θ (nlog 21. 9) 31

Randomized quicksort • Randomly choose an element as pivot – Every time need to do a partition, throw a die to decide which element to use as the pivot – Each element has 1/n probability to be selected Rand-Partition(A, p, r) d = random(); // a random number between 0 and 1 index = p + floor((r-p+1) * d); // p<=index<=r swap(A[p], A[index]); Partition(A, p, r); // now do partition using A[p] as pivot 3/9/2021 32

Running time of randomized quicksort T(n) = T(0) + T(n– 1) + n if 0 : n– 1 split, T(1) + T(n– 2) + n if 1 : n– 2 split, . . . T(n– 1) + T(0) + n if n– 1 : 0 split, • The expected running time is an (weighted) average of all cases Expectation 3/9/2021 33
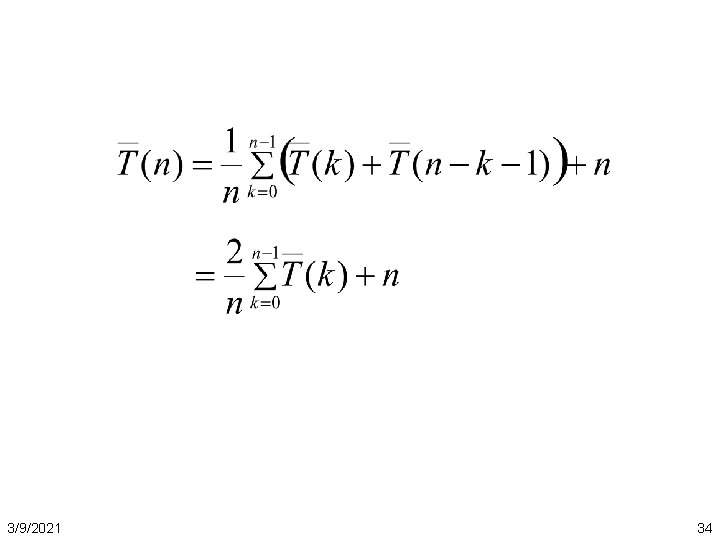
3/9/2021 34

Solving recurrence 1. Recursion tree (iteration) method - Good for guessing an answer 2. Substitution method - Generic method, rigid, but may be hard 3. Master method - Easy to learn, useful in limited cases only - Some tricks may help in other cases 3/9/2021 35

Substitution method The most general method to solve a recurrence (prove O and separately): 1. Guess the form of the solution: (e. g. using recursion trees, or expansion) 2. Verify by induction (inductive step). 3/9/2021 36

Expected running time of Quicksort • Guess • We need to show that for some c and sufficiently large n • Use T(n) instead of for convenience 3/9/2021 37

• Fact: • Need to show: T(n) ≤ c n log (n) • Assume: T(k) ≤ ck log (k) for 0 ≤ k ≤ n-1 • Proof: using the fact that if c ≥ 4. Therefore, by defintion, T(n) = (nlogn) 3/9/2021 38

Tightly Bounding The Key Summation Split the summation for a What we doing here? tighterare bound The lg are k inwe thedoing second term What here? is bounded by lg n Whatthe arelgwen doing here? Move outside the summation 3/9/2021 39

Tightly Bounding The Key Summation The summation bound so far The lg k in the first term is What are we doing here? bounded by lg n/2 = lg n we - 1 doing here? What are Move (lg n - 1) outside the What are we doing here? summation 3/9/2021 40

Tightly Bounding The Key Summation The summation bound so far Distribute the (lg nhere? - 1) What are we doing The summations overlap in What are we doing here? range; combine them The. What Guassian are weseries doing here? 3/9/2021 41

Tightly Bounding The Key Summation The summation bound so far Rearrange first term, place What are we doing here? upper bound on second Guassian series What are we doing? Multiply it What are we doing? all out 3/9/2021 42

Tightly Bounding The Key Summation 3/9/2021 43
 Heap sort vs selection sort
Heap sort vs selection sort Quick sort merge sort
Quick sort merge sort Quick sort merge sort
Quick sort merge sort Difference between insertion sort and bubble sort
Difference between insertion sort and bubble sort How selection sort works
How selection sort works Bubble sort 5-66
Bubble sort 5-66 Difference between bubble sort and selection sort
Difference between bubble sort and selection sort Quick find vs quick union
Quick find vs quick union Velocity and acceleration quick check
Velocity and acceleration quick check Selection sort worst case
Selection sort worst case Loop invariant quicksort
Loop invariant quicksort Is quick sort in place
Is quick sort in place Analysis of quicksort
Analysis of quicksort Quick sort algorithm
Quick sort algorithm Slowest sorting algorithm
Slowest sorting algorithm Algoritma merge sort
Algoritma merge sort Quickselect
Quickselect Quick sort
Quick sort Quick sort
Quick sort Complexity analysis examples
Complexity analysis examples Quick sort worst complexity
Quick sort worst complexity Linked list quicksort
Linked list quicksort Quick sort
Quick sort Radix sort clasificacion
Radix sort clasificacion Quick sort
Quick sort Quick sort algorithm with example
Quick sort algorithm with example Bubble sort vs selection sort
Bubble sort vs selection sort Pseudo code of bubble sort
Pseudo code of bubble sort Counting sort animation
Counting sort animation Radix bucket sort
Radix bucket sort 1001 design
1001 design Association analysis: basic concepts and algorithms
Association analysis: basic concepts and algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Probabilistic analysis and randomized algorithms
Probabilistic analysis and randomized algorithms Introduction of design and analysis of algorithms
Introduction of design and analysis of algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Binary search in design and analysis of algorithms
Binary search in design and analysis of algorithms Introduction to the design and analysis of algorithms
Introduction to the design and analysis of algorithms Design and analysis of algorithms
Design and analysis of algorithms Design and analysis of algorithms
Design and analysis of algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Comp 482
Comp 482