Sorting Algorithms Merge Sort Quick Sort Hairong Zhao

Sorting Algorithms Merge Sort Quick Sort Hairong Zhao http: //web. njit. edu/~hz 2 New Jersey Institute of Technology

Overview l Divide and Conquer l Merge Sort l Quick Sort 2

Divide and Conquer 1. Base Case, solve the problem directly if it is small enough 2. Divide the problem into two or more similar and smaller subproblems 3. Recursively solve the subproblems 4. Combine solutions to the subproblems 3

Divide and Conquer - Sort Problem: l Input: A[left. . right] – unsorted array of integers l Output: A[left. . right] – sorted in non-decreasing order 4

Divide and Conquer - Sort 1. Base case at most one element (left ≥ right), return 2. Divide A into two subarrays: First. Part, Second. Part Two Subproblems: sort the First. Part sort the Second. Part 3. Recursively sort First. Part sort Second. Part 4. Combine sorted First. Part and sorted Second. Part 5

Overview l Divide and Conquer l Merge Sort l Quick Sort 6

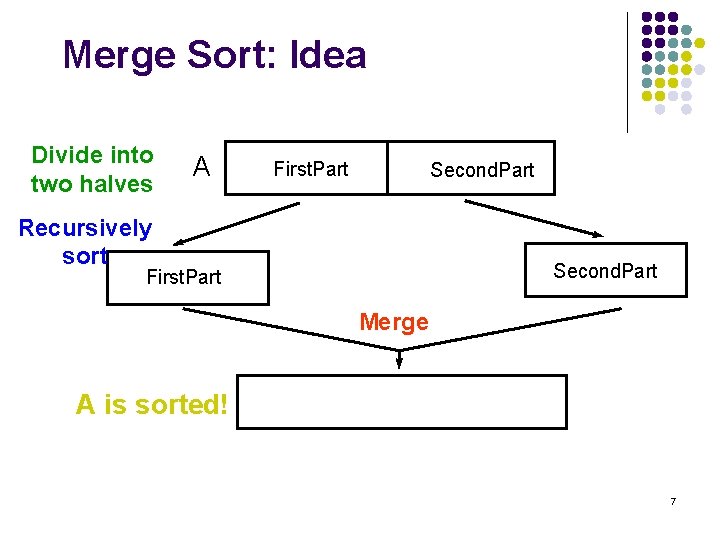
Merge Sort: Idea Divide into two halves A First. Part Second. Part Recursively sort Second. Part First. Part Merge A is sorted! 7

Merge Sort: Algorithm Merge-Sort (A, left, right) if left ≥ right return else middle ← b(left+right)/2 Merge-Sort(A, left, middle) Recursive Call Merge-Sort(A, middle+1, right) Merge(A, left, middle, right) 8

Merge-Sort: Merge Sorted A: merge Sorted First. Part Sorted Second. Part A: A[left] A[middle] A[right] 9

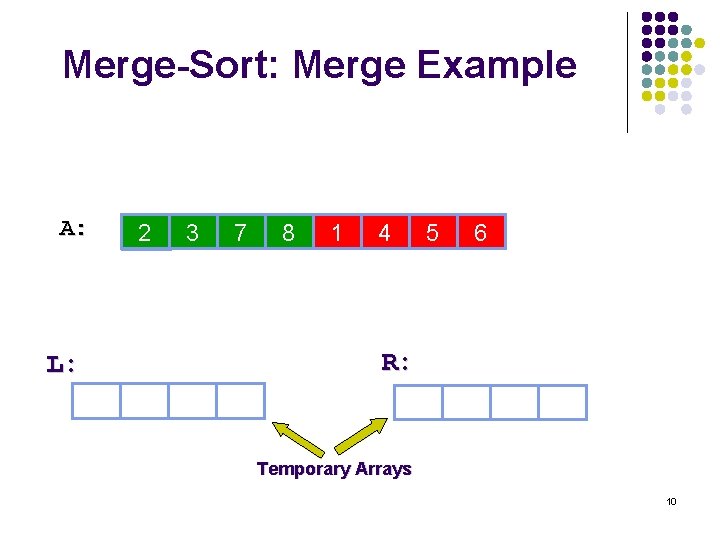
Merge-Sort: Merge Example A: 2 5 3 5 7 28 8 30 1 15 4 6 5 14 6 10 R: L: 3 5 15 28 6 10 14 22 Temporary Arrays 10

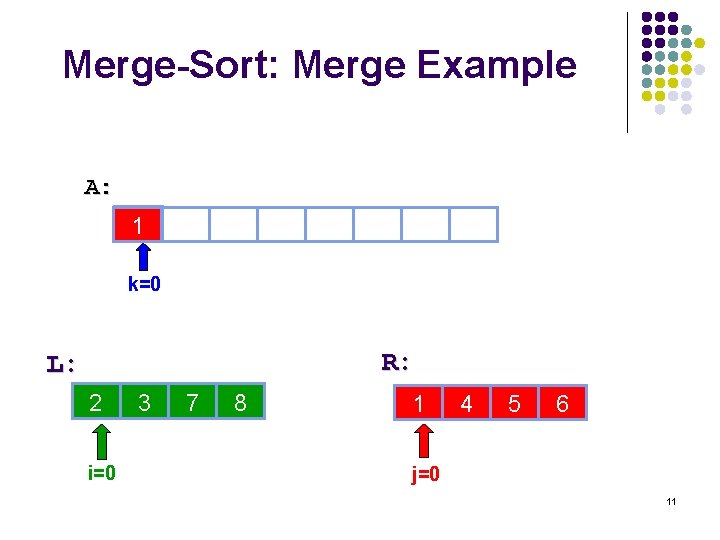
Merge-Sort: Merge Example A: 3 1 5 15 28 30 6 10 14 k=0 R: L: 3 2 i=0 15 3 28 7 30 8 6 1 10 4 14 5 22 6 j=0 11

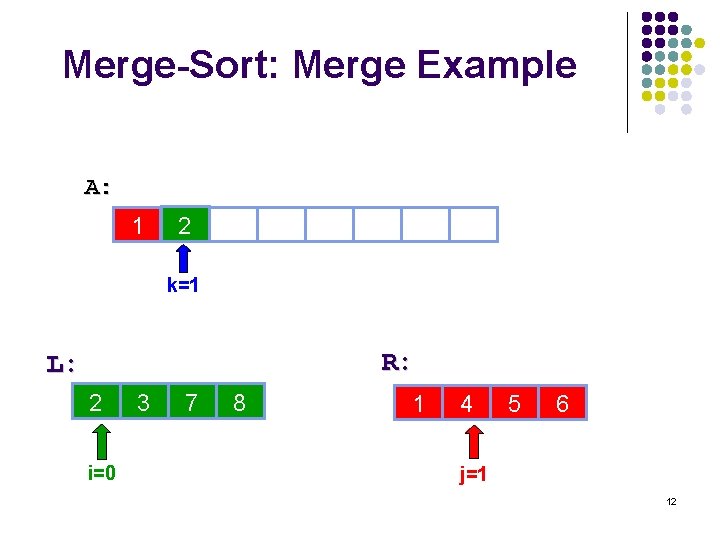
Merge-Sort: Merge Example A: 1 2 5 15 28 30 6 10 14 k=1 R: L: 3 2 i=0 5 3 15 7 28 8 6 1 10 4 14 5 22 6 j=1 12

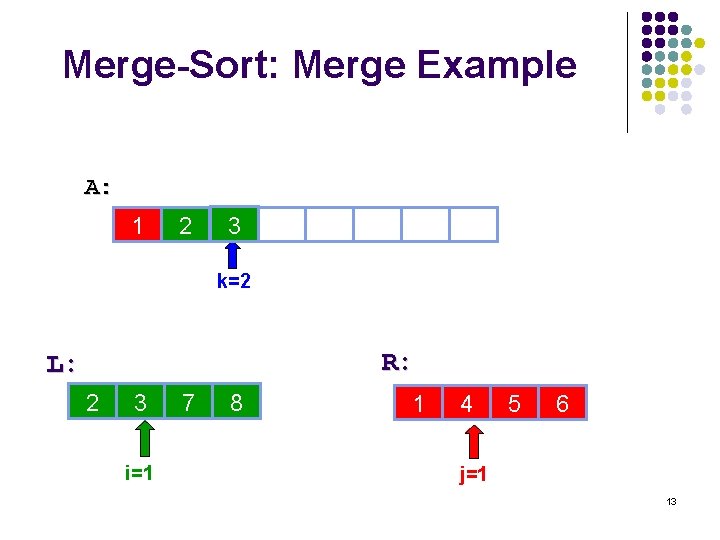
Merge-Sort: Merge Example A: 1 2 3 28 30 15 6 10 14 k=2 R: L: 2 3 i=1 7 8 6 1 10 4 14 5 22 6 j=1 13

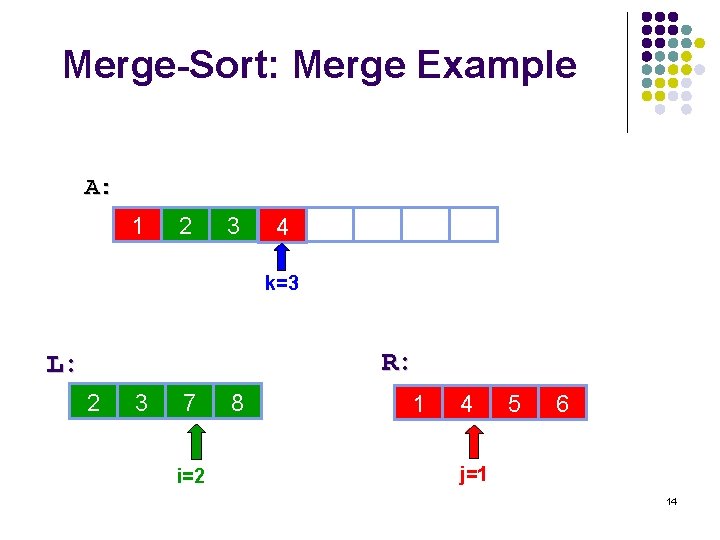
Merge-Sort: Merge Example A: 1 2 3 4 6 10 14 k=3 R: L: 2 3 7 i=2 8 6 1 10 4 14 5 22 6 j=1 14

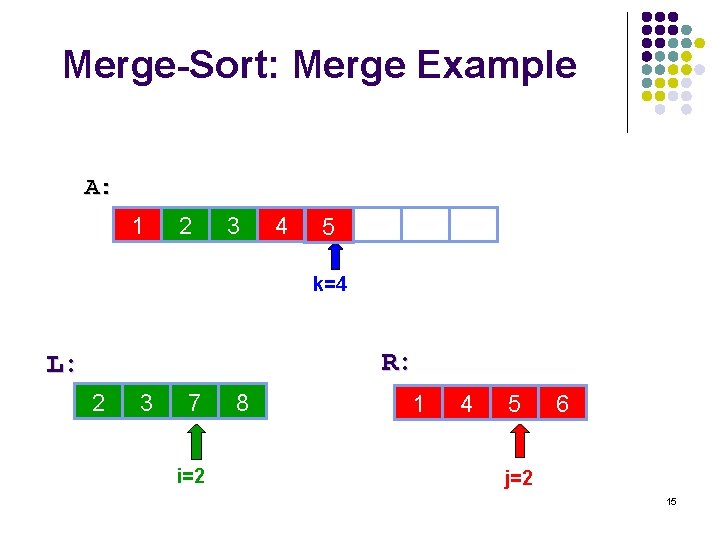
Merge-Sort: Merge Example A: 1 2 3 4 5 6 10 14 k=4 R: L: 2 3 7 i=2 8 6 1 10 4 14 5 22 6 j=2 15

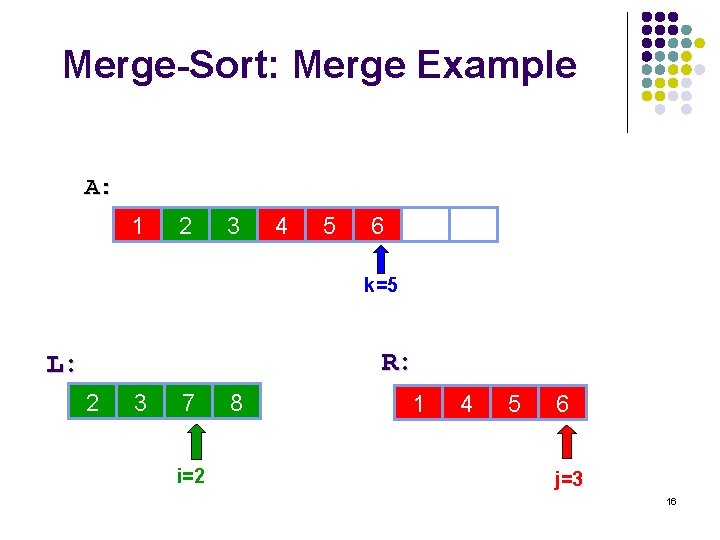
Merge-Sort: Merge Example A: 1 2 3 4 5 6 10 14 k=5 R: L: 2 3 7 i=2 8 6 1 10 4 14 5 22 6 j=3 16

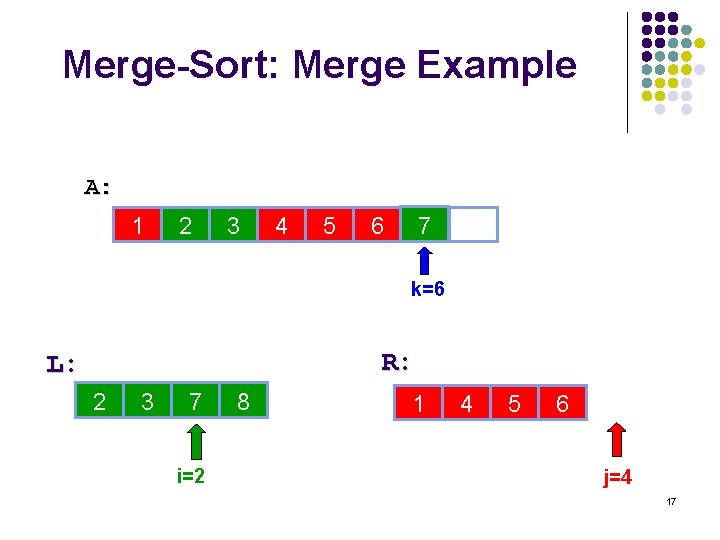
Merge-Sort: Merge Example A: 1 2 3 4 5 7 6 14 k=6 R: L: 2 3 7 i=2 8 6 1 10 4 14 5 22 6 j=4 17

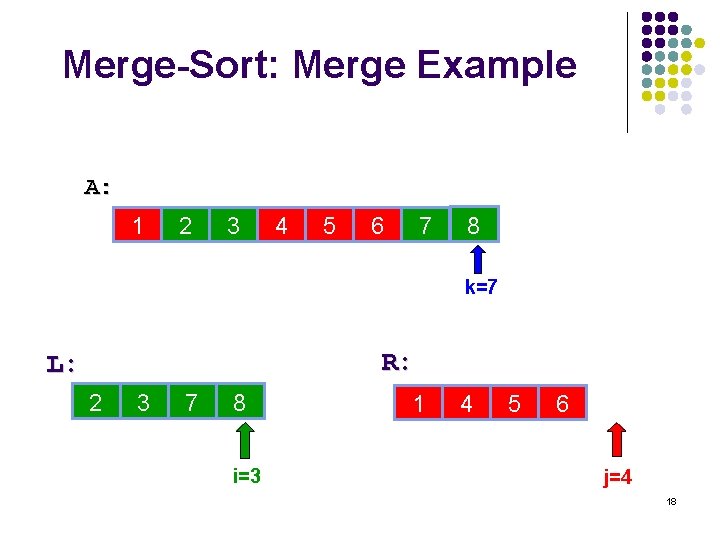
Merge-Sort: Merge Example A: 1 2 3 4 5 6 7 8 14 k=7 R: L: 3 2 5 3 15 7 28 8 i=3 6 1 10 4 14 5 22 6 j=4 18

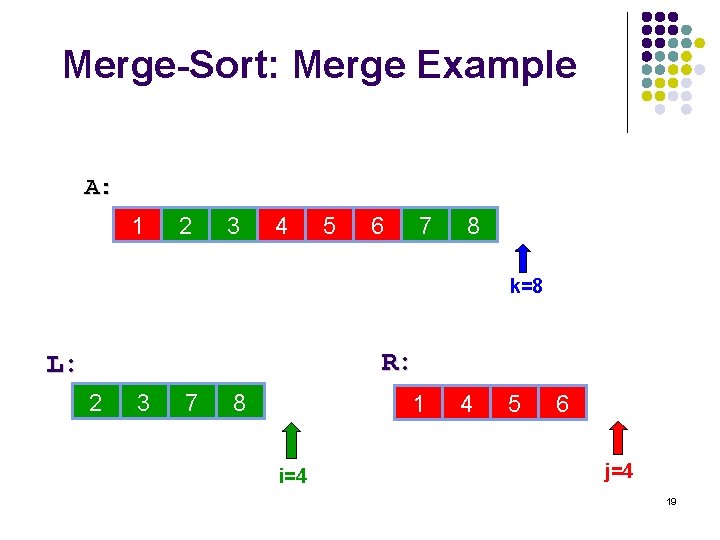
Merge-Sort: Merge Example A: 1 2 3 4 5 6 7 8 k=8 R: L: 3 2 5 3 15 7 28 8 6 1 i=4 10 4 14 5 22 6 j=4 19

Merge(A, left, middle, right) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. n 1 ← middle – left + 1 n 2 ← right – middle create array L[n 1], R[n 2] for i ← 0 to n 1 -1 do L[i] ← A[left +i] for j ← 0 to n 2 -1 do R[j] ← A[middle+j] k ← i ← j ← 0 while i < n 1 & j < n 2 if L[i] < R[j] A[k++] ← L[i++] else A[k++] ← R[j++] while i < n 1 A[k++] ← L[i++] while j < n 2 A[k++] ← R[j++] n = n +n 1 2 Space: n Time : cn for some constant c 20

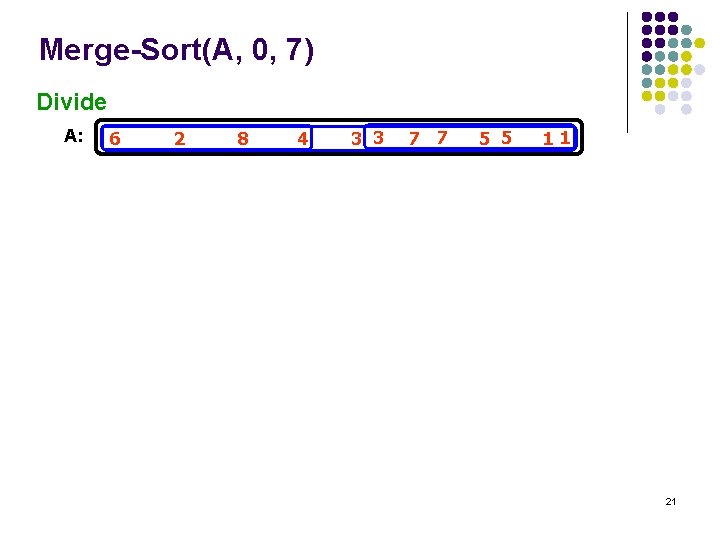
Merge-Sort(A, 0, 7) Divide A: 6 2 8 4 3 3 7 7 5 5 11 21

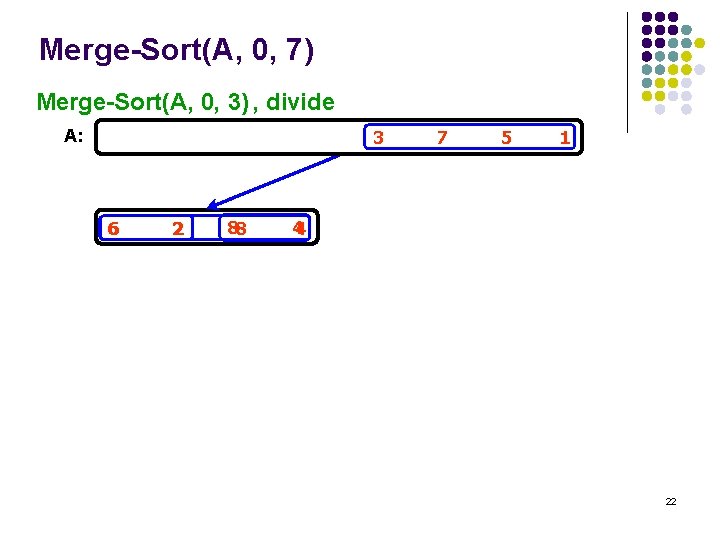
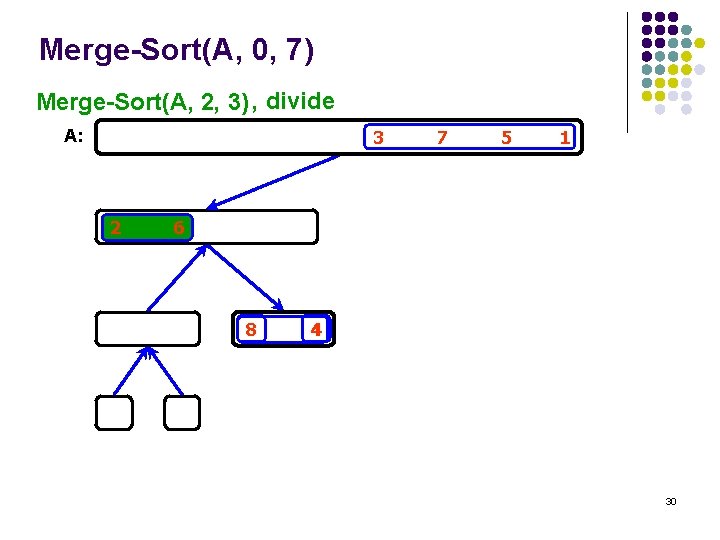
Merge-Sort(A, 0, 7) Merge-Sort(A, 0, 3) , divide A: 3 6 2 88 7 5 1 44 22

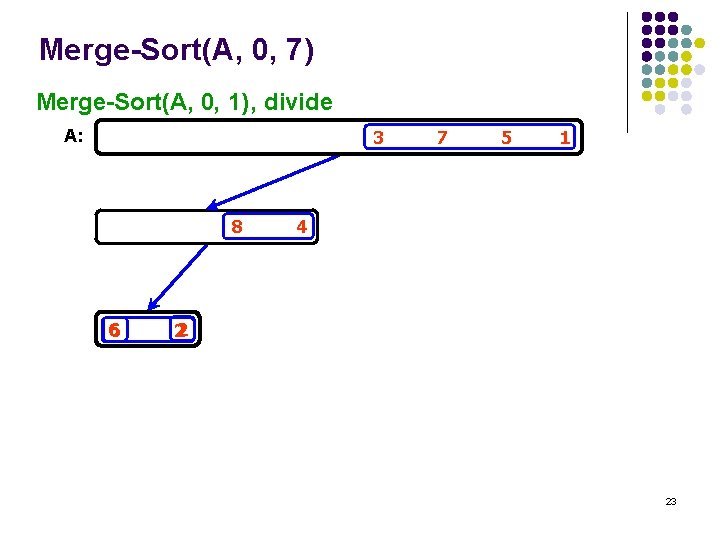
Merge-Sort(A, 0, 7) Merge-Sort(A, 0, 1) , divide A: 3 8 6 7 5 1 4 2 2 23

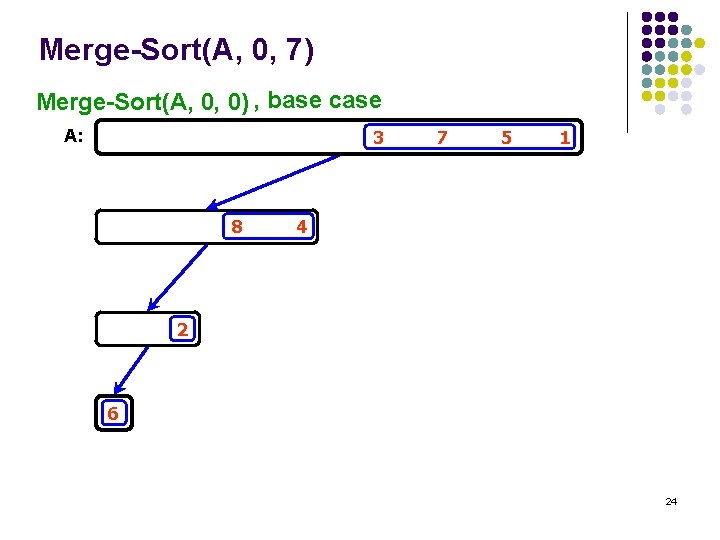
Merge-Sort(A, 0, 7) Merge-Sort(A, 0, 0) , base case A: 3 8 7 5 1 4 2 6 24

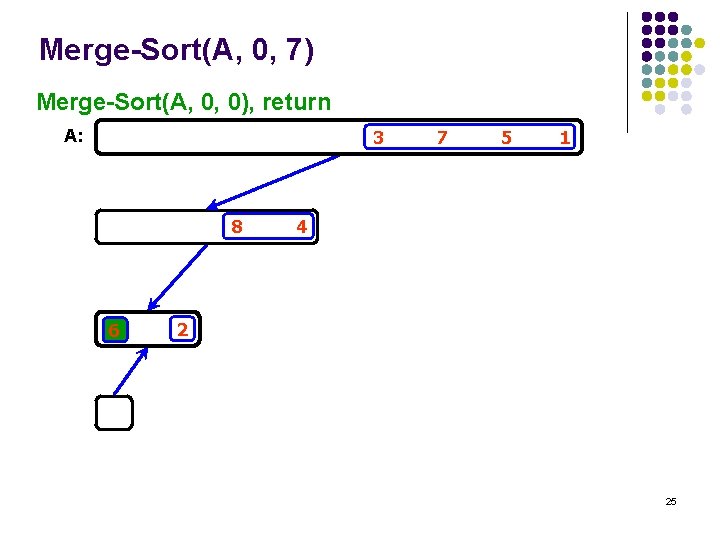
Merge-Sort(A, 0, 7) Merge-Sort(A, 0, 0), return A: 3 8 6 7 5 1 4 2 25

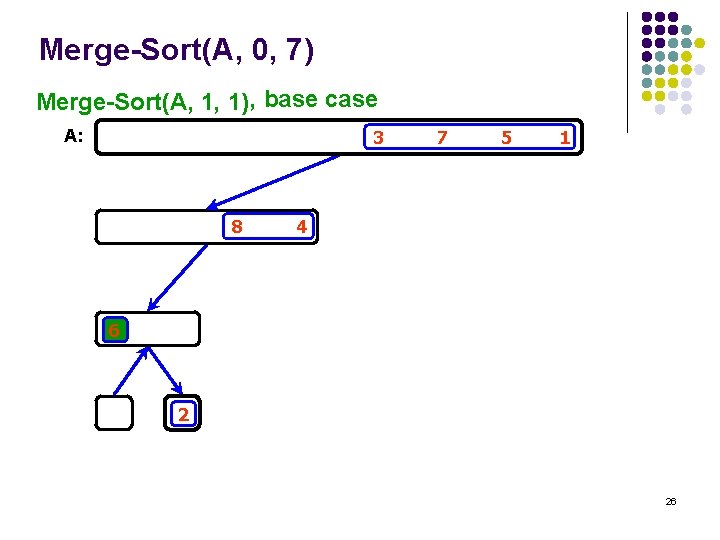
Merge-Sort(A, 0, 7) Merge-Sort(A, 1, 1) , base case A: 3 8 7 5 1 4 6 2 26

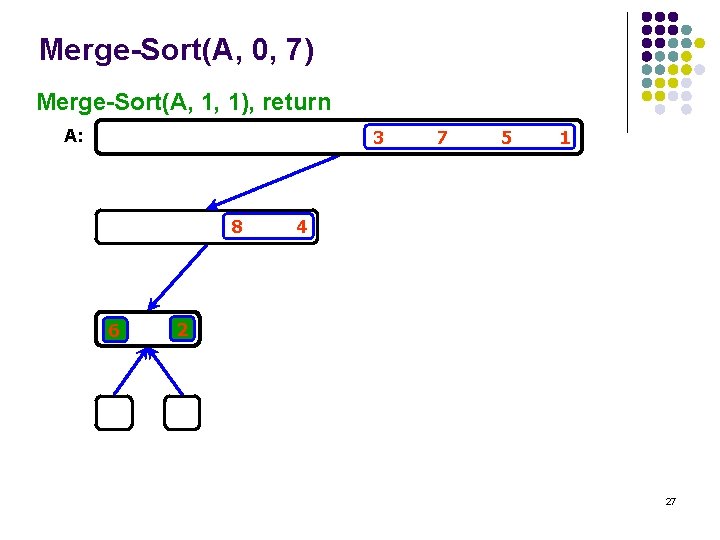
Merge-Sort(A, 0, 7) Merge-Sort(A, 1, 1), return A: 3 8 6 7 5 1 4 2 27

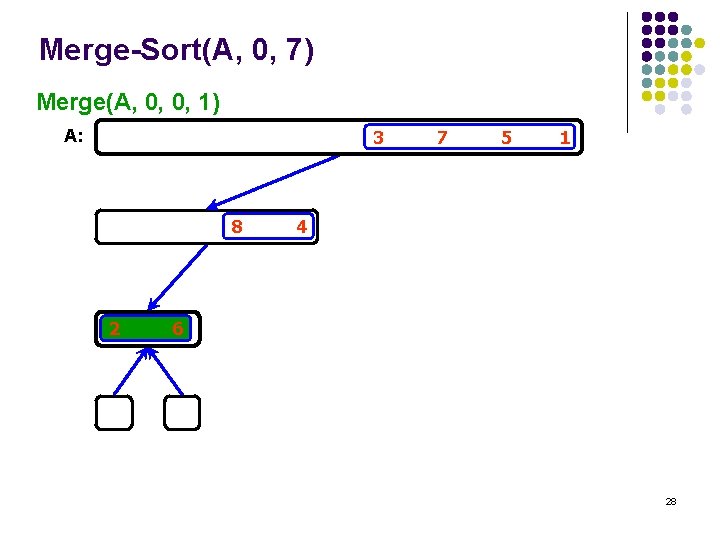
Merge-Sort(A, 0, 7) Merge(A, 0, 0, 1) A: 3 8 2 7 5 1 4 6 28

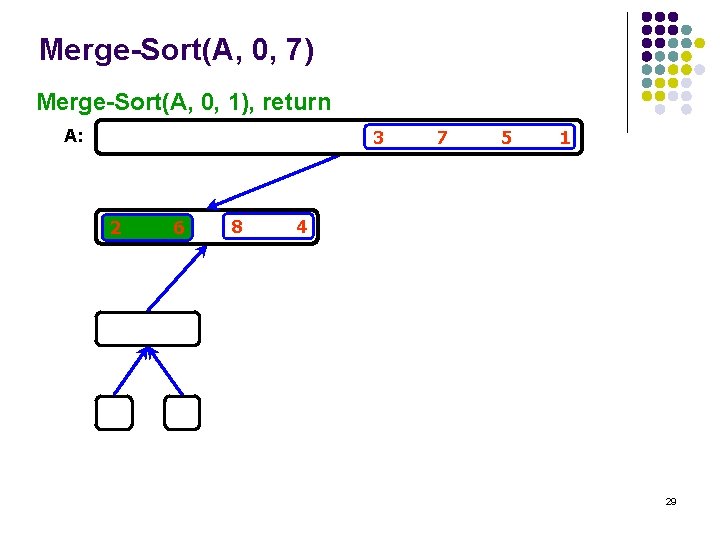
Merge-Sort(A, 0, 7) Merge-Sort(A, 0, 1), return A: 3 2 6 8 7 5 1 4 29

Merge-Sort(A, 0, 7) Merge-Sort(A, 2, 3) , divide A: 3 2 7 5 1 6 8 4 30

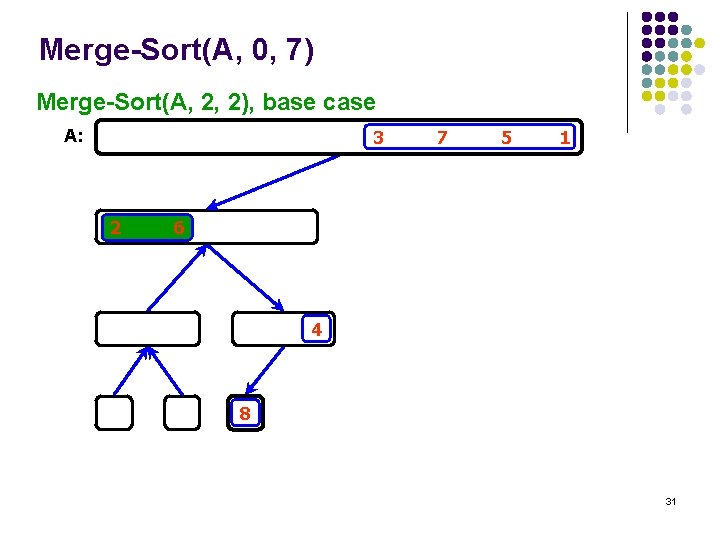
Merge-Sort(A, 0, 7) Merge-Sort(A, 2, 2), base case A: 3 2 7 5 1 6 4 8 31

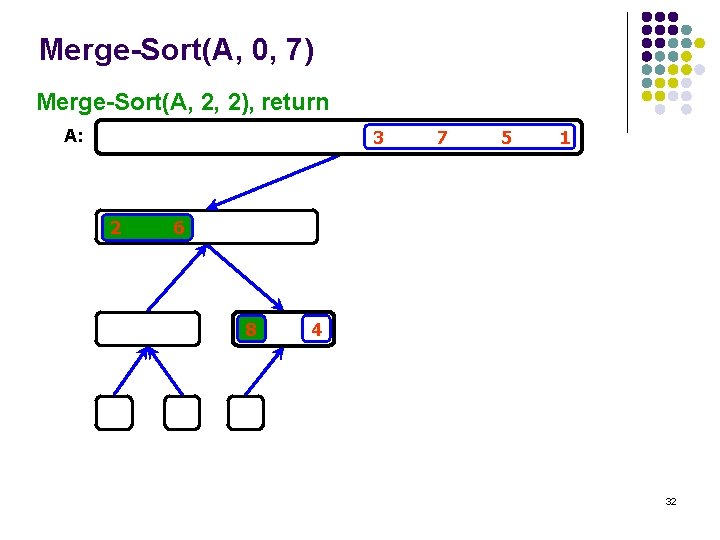
Merge-Sort(A, 0, 7) Merge-Sort(A, 2, 2), return A: 3 2 7 5 1 6 8 4 32

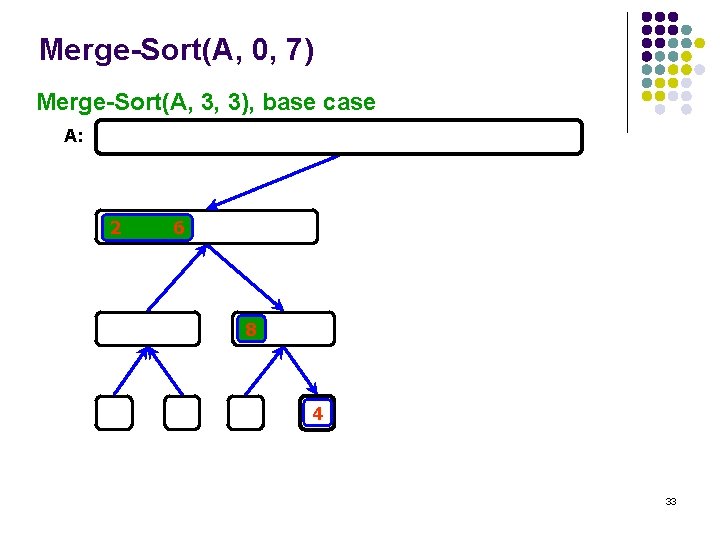
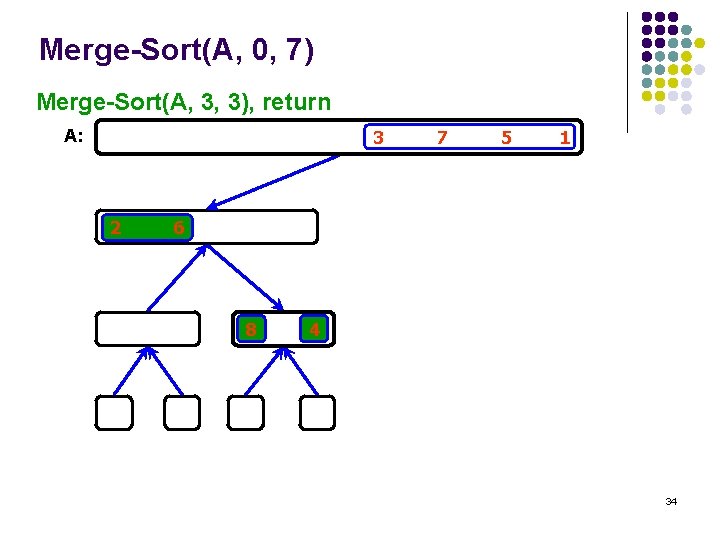
Merge-Sort(A, 0, 7) Merge-Sort(A, 3, 3), base case A: 2 6 8 4 33

Merge-Sort(A, 0, 7) Merge-Sort(A, 3, 3), return A: 3 2 7 5 1 6 8 4 34

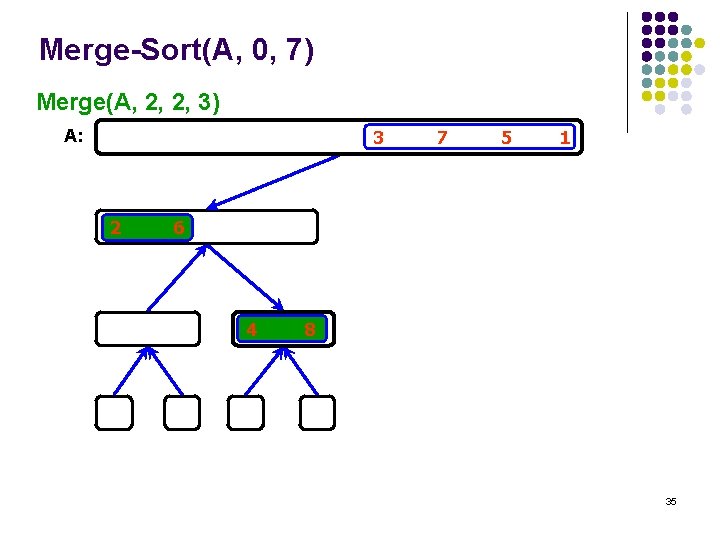
Merge-Sort(A, 0, 7) Merge(A, 2, 2, 3) A: 3 2 7 5 1 6 4 8 35

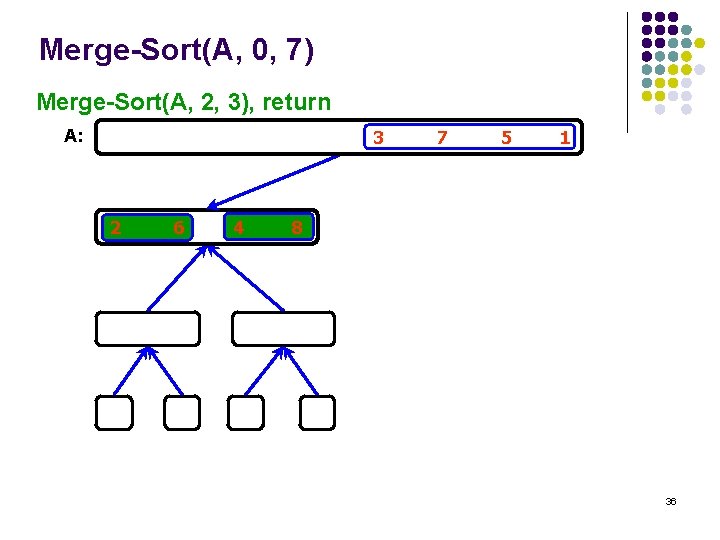
Merge-Sort(A, 0, 7) Merge-Sort(A, 2, 3), return A: 3 2 6 4 7 5 1 8 36

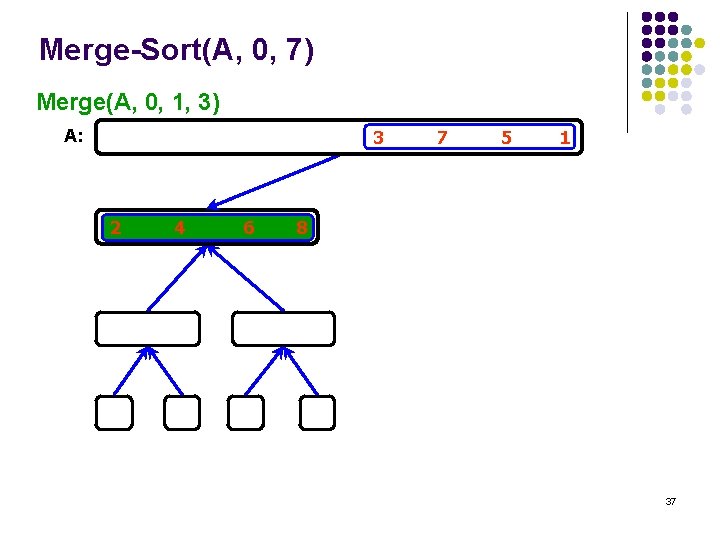
Merge-Sort(A, 0, 7) Merge(A, 0, 1, 3) A: 3 2 4 6 7 5 1 8 37

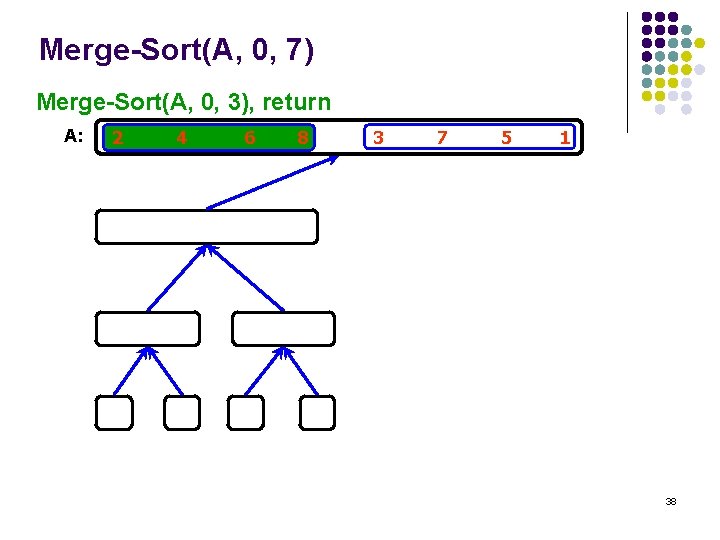
Merge-Sort(A, 0, 7) Merge-Sort(A, 0, 3), return A: 2 4 6 8 3 7 5 1 38

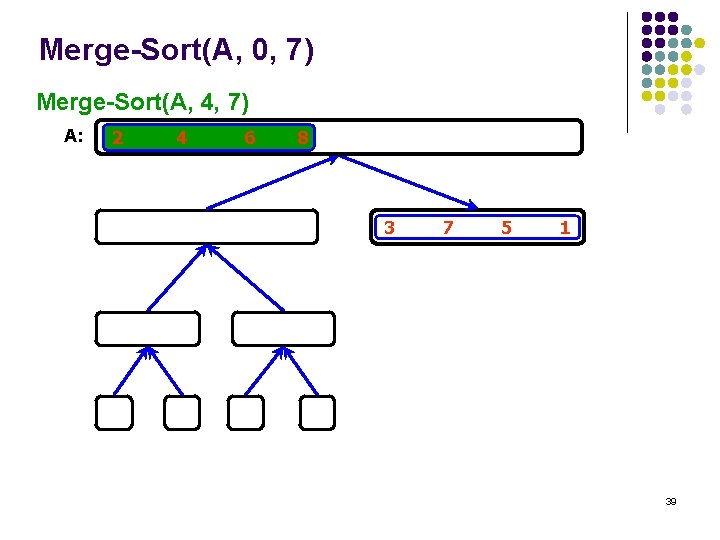
Merge-Sort(A, 0, 7) Merge-Sort(A, 4, 7) A: 2 4 6 8 3 7 5 1 39

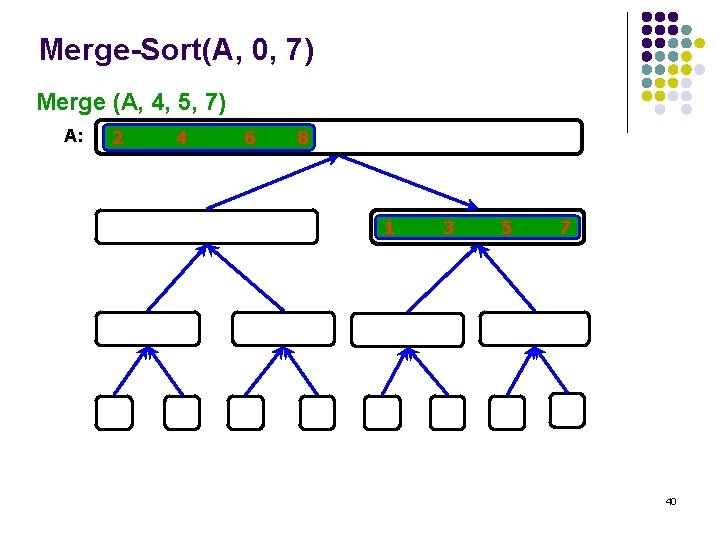
Merge-Sort(A, 0, 7) Merge (A, 4, 5, 7) A: 2 4 6 8 1 3 5 7 40

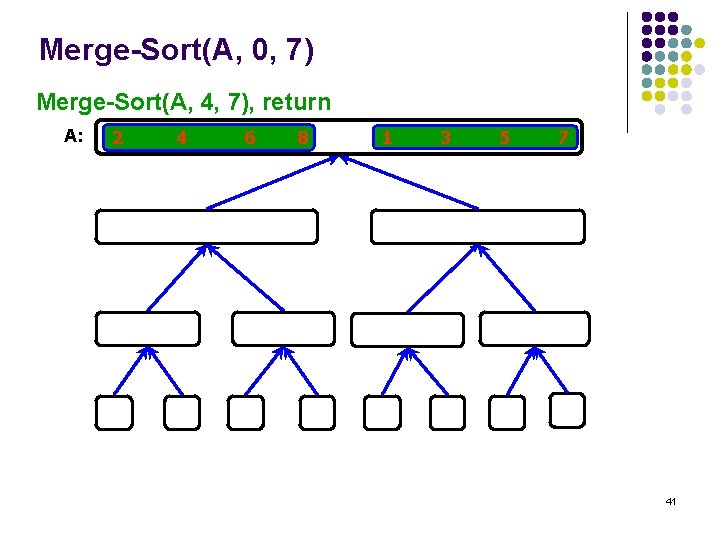
Merge-Sort(A, 0, 7) Merge-Sort(A, 4, 7), return A: 2 4 6 8 1 3 5 7 41

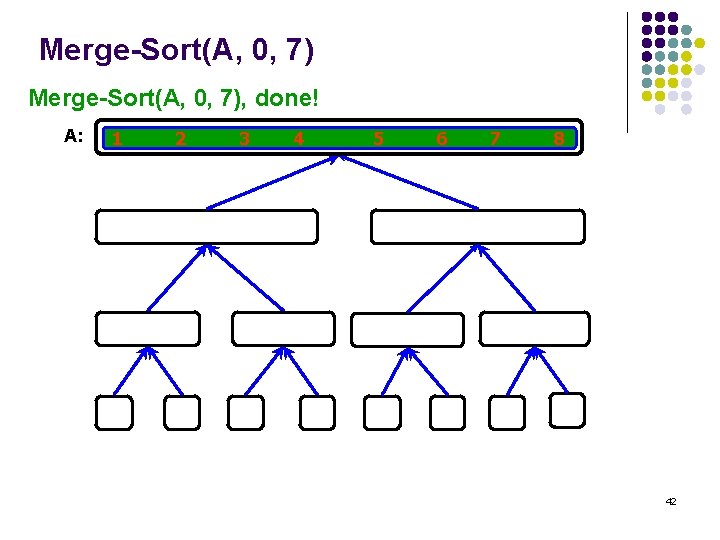
Merge-Sort(A, 0, 7) Merge-Sort(A, Merge(A, 0, 3, 0, 7)7), done! A: 1 2 3 4 5 6 7 8 42

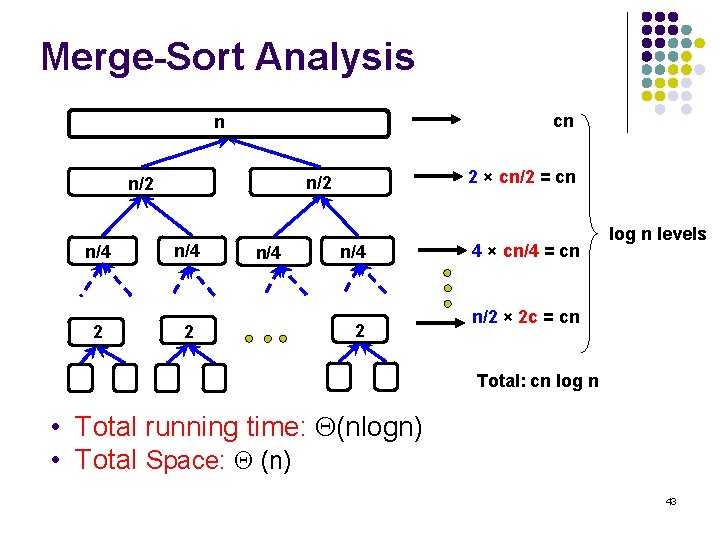
Merge-Sort Analysis cn n n/4 2 2 × cn/2 = cn n/2 n/4 2 4 × cn/4 = cn log n levels n/2 × 2 c = cn Total: cn log n • Total running time: (nlogn) • Total Space: (n) 43

Merge-Sort Summary Approach: divide and conquer Time l l Most of the work is in the merging Total time: (n log n) Space: l (n), more space than other sorts. 44

Overview l Divide and Conquer l Merge Sort l Quick Sort 45

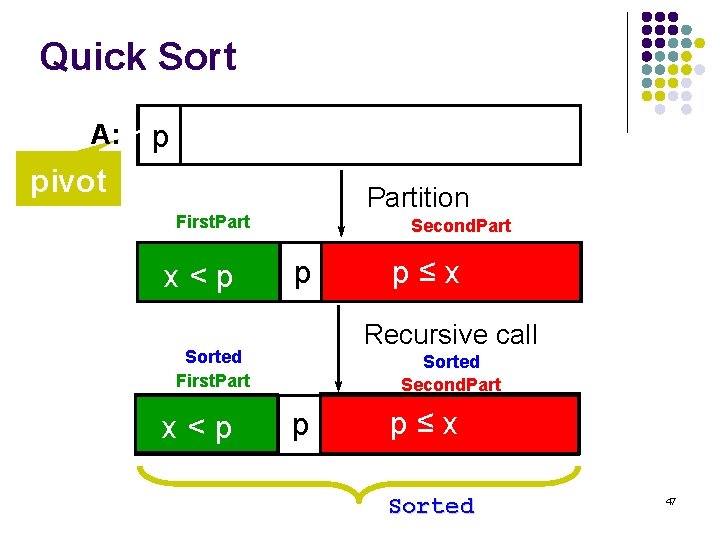
Quick Sort l Divide: l l Pick any element p as the pivot, e. g, the first element Partition the remaining elements into First. Part, which contains all elements < p Second. Part, which contains all elements ≥ p l Recursively sort the First. Part and Second. Part l Combine: no work is necessary since sorting is done in place 46

Quick Sort A: p pivot Partition First. Part x<p Second. Part p Recursive call Sorted First. Part x<p p≤x Sorted Second. Part p p≤x Sorted 47

Quick Sort Quick-Sort(A, left, right) if left ≥ right return else middle ← Partition(A, left, right) Quick-Sort(A, left, middle– 1 ) Quick-Sort(A, middle+1, right) end if 48

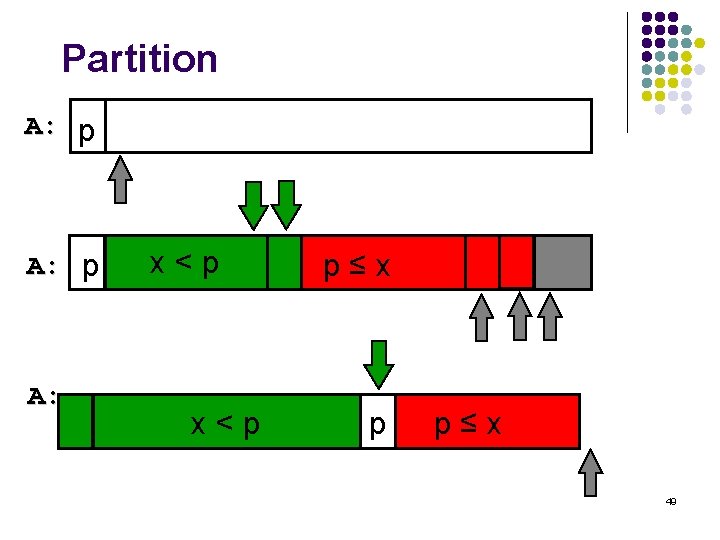
Partition A: p A: p x<p p≤x 49

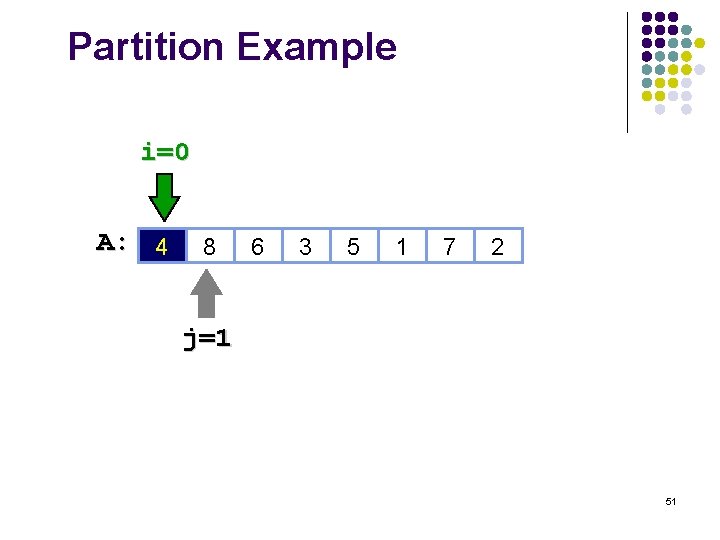
Partition Example A: 4 8 6 3 5 1 7 2 50

Partition Example i=0 A: 4 8 6 3 5 1 7 2 j=1 51

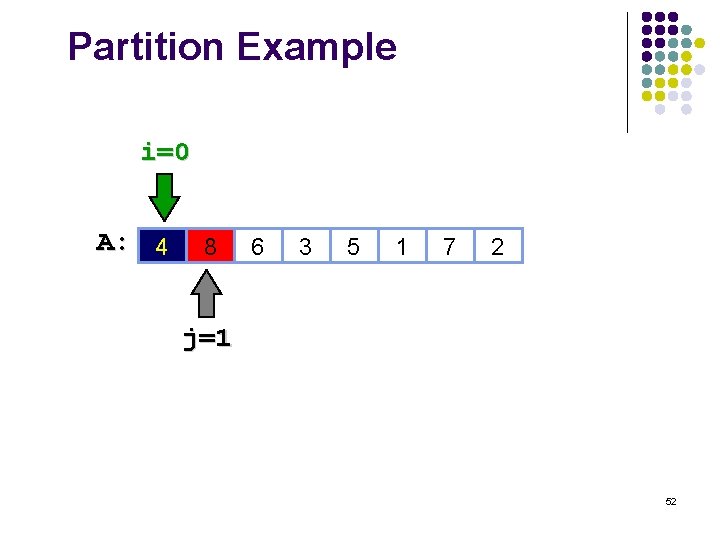
Partition Example i=0 A: 4 8 6 3 5 1 7 2 j=1 52

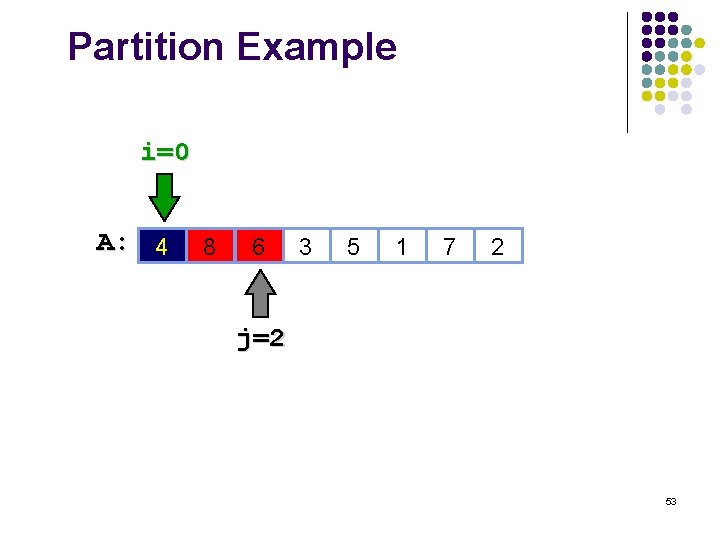
Partition Example i=0 A: 4 8 6 3 5 1 7 2 j=2 53

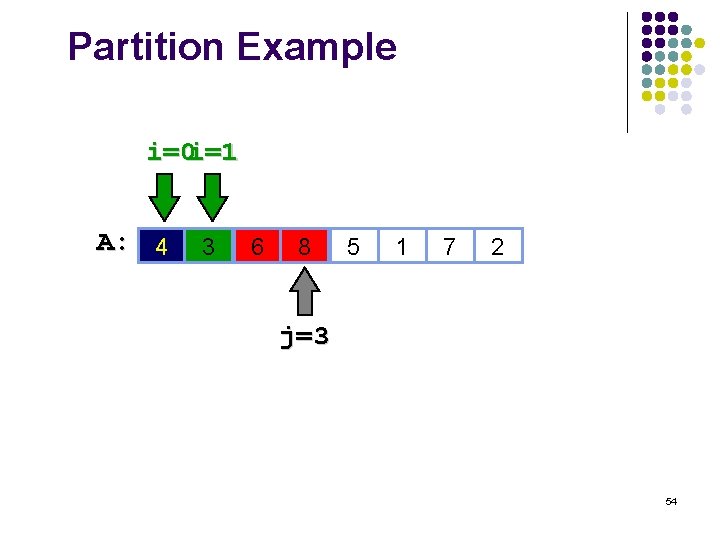
Partition Example i=0 i=1 A: 4 8 3 6 3 8 5 1 7 2 j=3 54

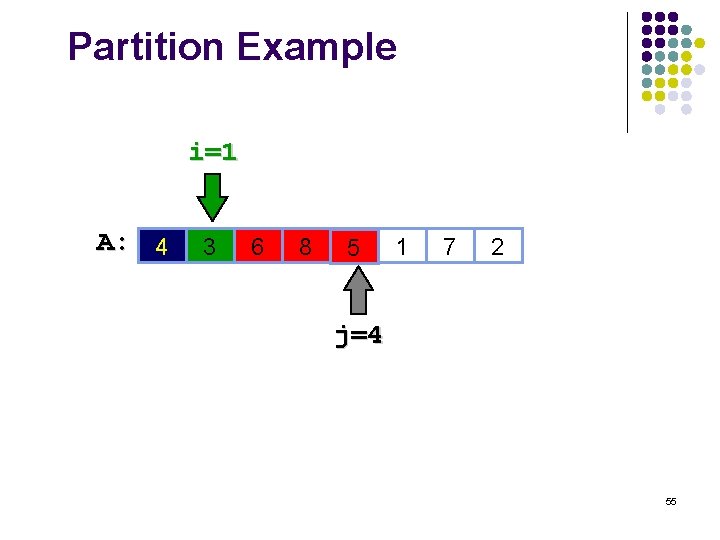
Partition Example i=1 A: 4 3 6 8 5 1 7 2 j=4 55

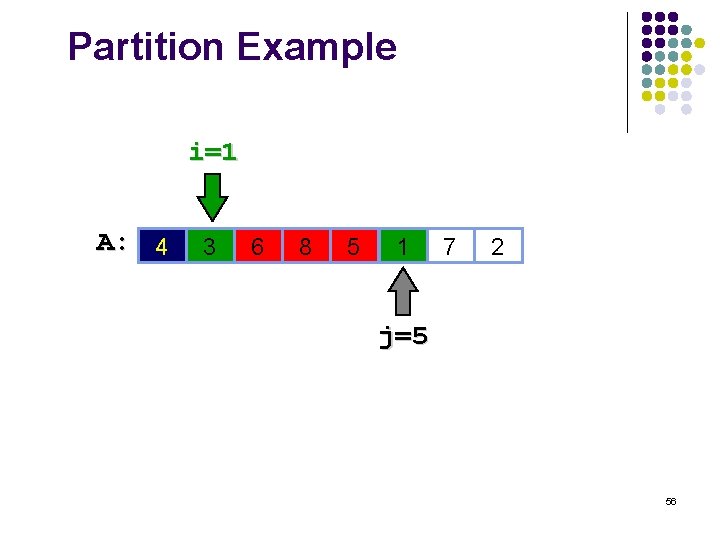
Partition Example i=1 A: 4 3 6 8 5 1 7 2 j=5 56

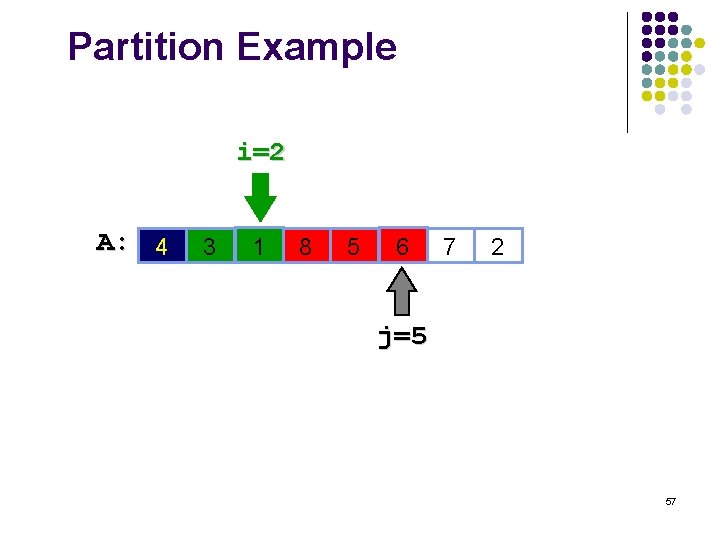
Partition Example i=2 A: 4 3 1 6 8 5 6 1 7 2 j=5 57

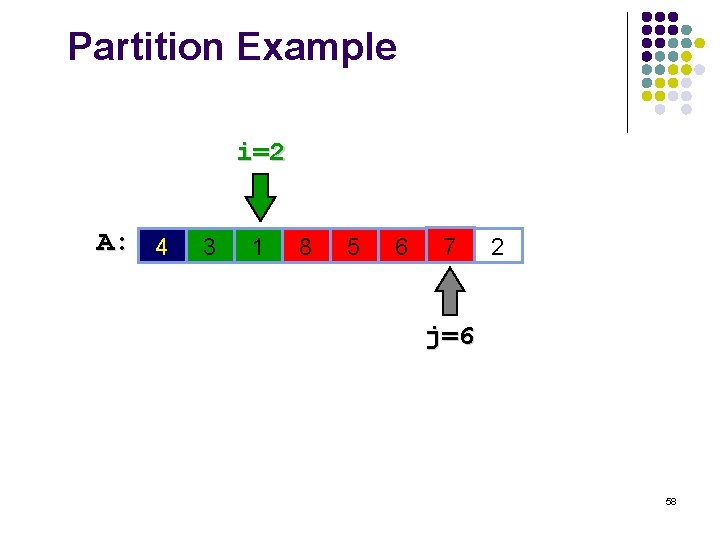
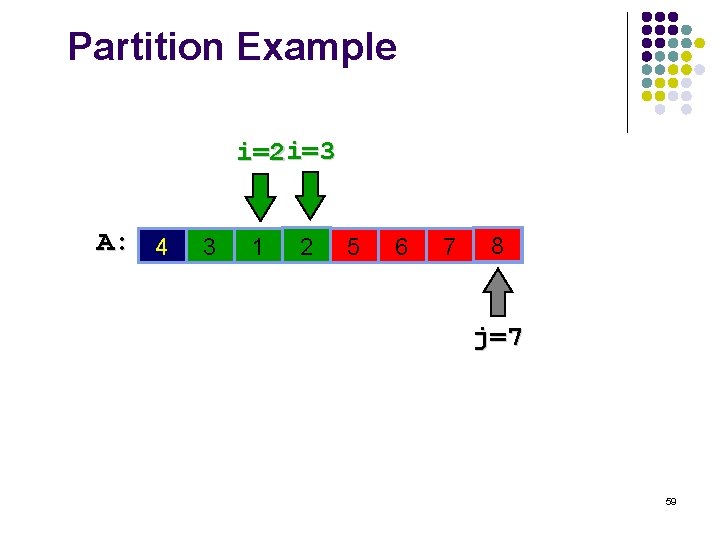
Partition Example i=2 A: 4 3 1 8 5 6 7 2 j=6 58

Partition Example i=2 i=3 A: 4 3 1 2 8 5 6 7 8 2 j=7 59

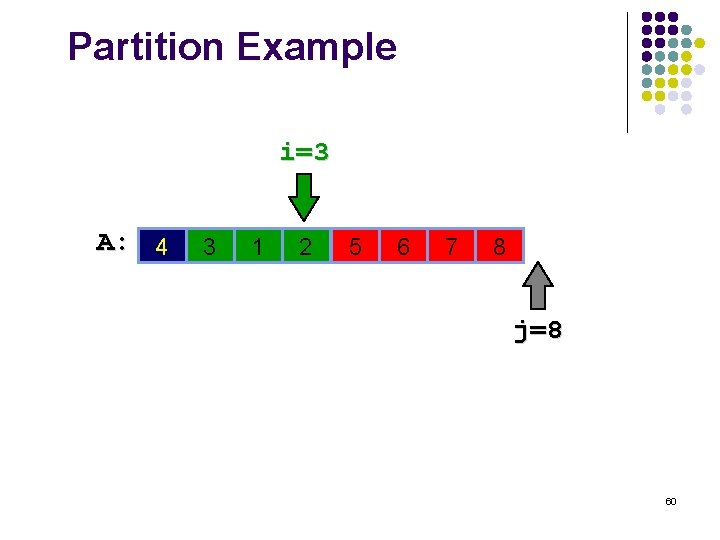
Partition Example i=3 A: 4 3 1 2 5 6 7 8 j=8 60

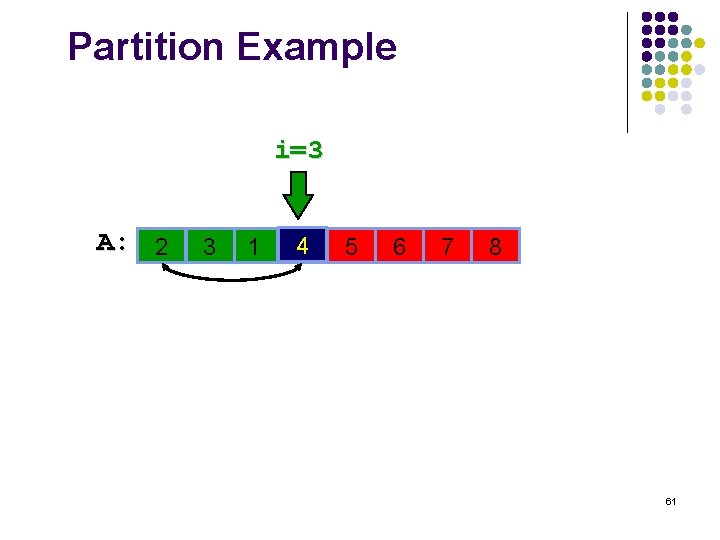
Partition Example i=3 A: 24 3 1 4 2 5 6 7 8 61

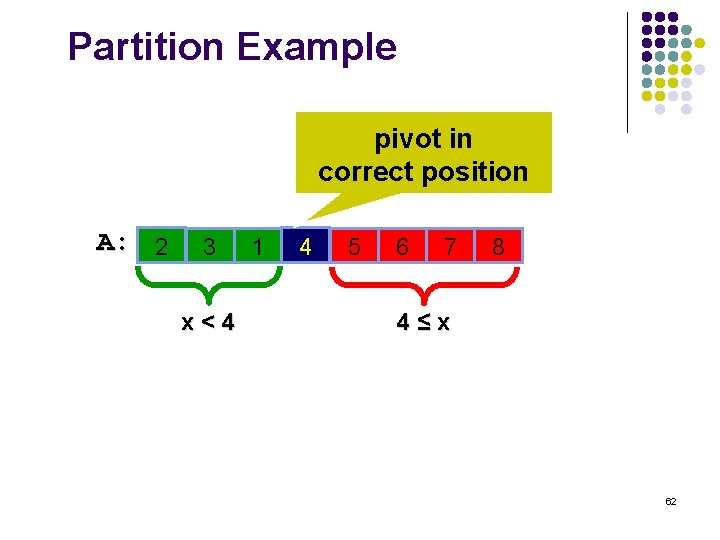
Partition Example pivot in correct position A: 2 3 x<4 1 4 5 6 7 8 4≤x 62

Partition(A, left, right) 1. x ← A[left] 2. i ← left 3. for j ← left+1 to right 4. if A[j] < x then 5. i ← i + 1 6. swap(A[i], A[j]) 7. end if 8. end for j 9. swap(A[i], A[left]) 10. return i n = right – left +1 Time: cn for some constant c Space: constant 63

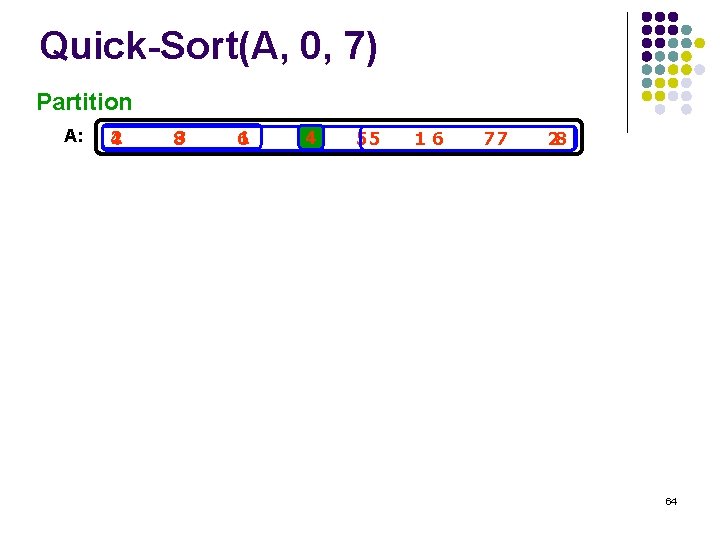
Quick-Sort(A, 0, 7) Partition A: 2 4 3 8 1 6 34 55 16 77 28 64

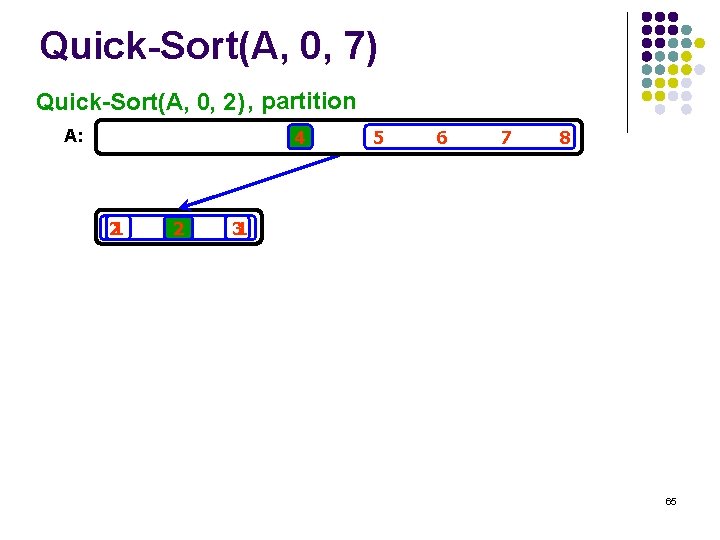
Quick-Sort(A, 0, 7) Quick-Sort(A, 0, 2) , partition A: 4 21 2 3 5 6 7 8 31 65

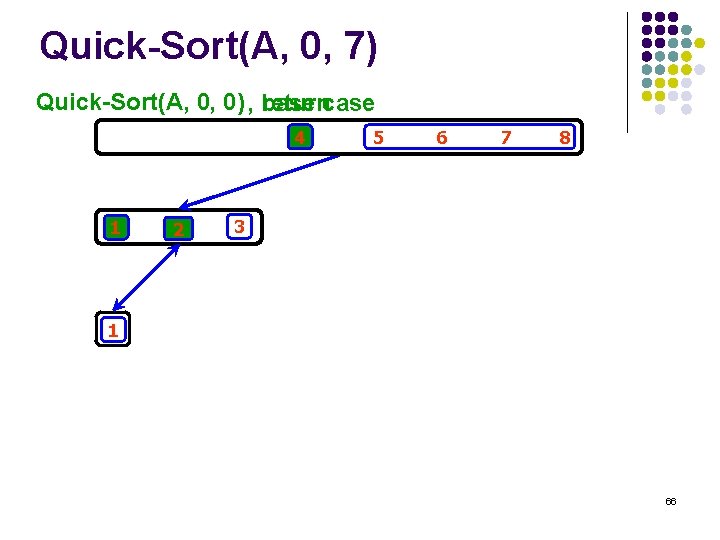
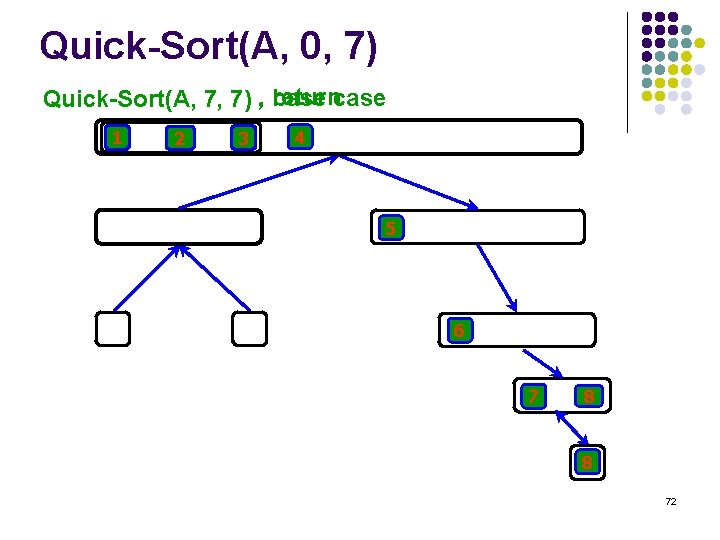
Quick-Sort(A, 0, 7) Quick-Sort(A, 0, 0) , base returncase 4 1 2 5 6 7 8 3 1 66

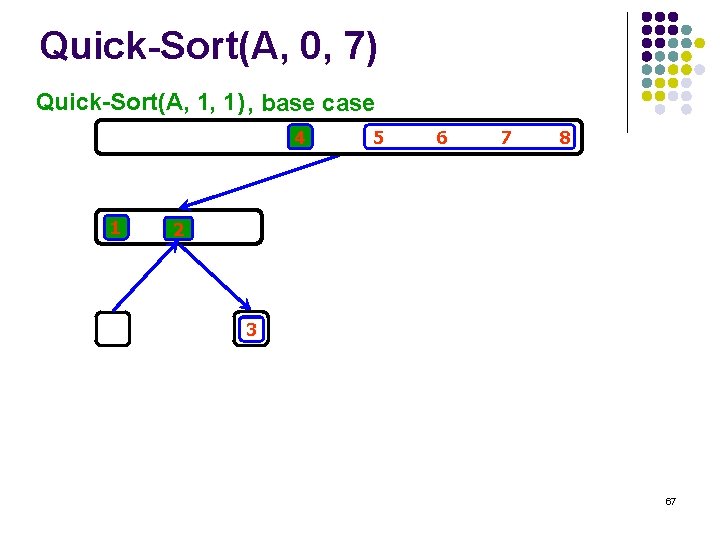
Quick-Sort(A, 0, 7) Quick-Sort(A, 1, 1) , base case 4 1 5 6 7 8 2 3 67

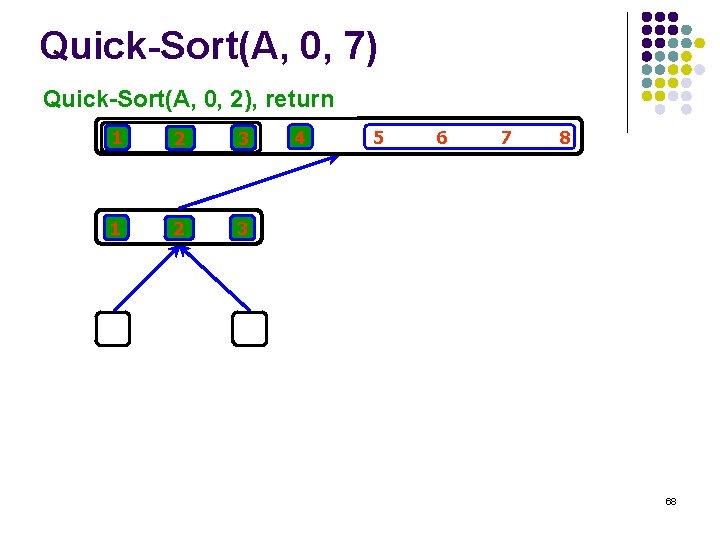
Quick-Sort(A, 0, 7) Quick-Sort(A, 2, 0, 2), return Quick-Sort(A, 1 2 3 4 5 6 7 8 68

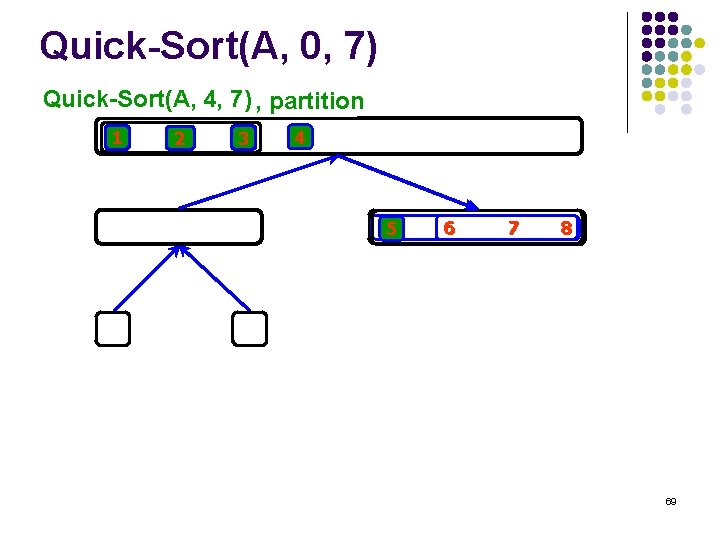
Quick-Sort(A, 0, 7) Quick-Sort(A, 2, 4, 2), 7) , return partition Quick-Sort(A, 1 2 3 4 55 6 7 8 69

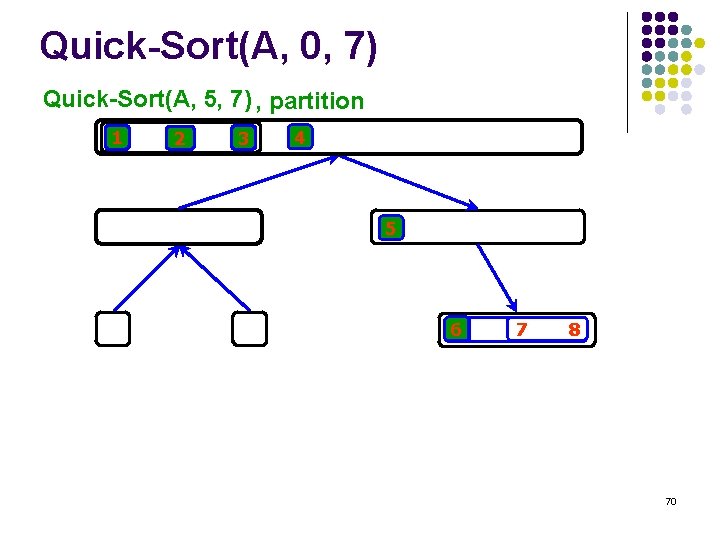
Quick-Sort(A, 0, 7) Quick-Sort(A, 5, 7) , partition 1 2 3 4 5 6 6 7 8 70

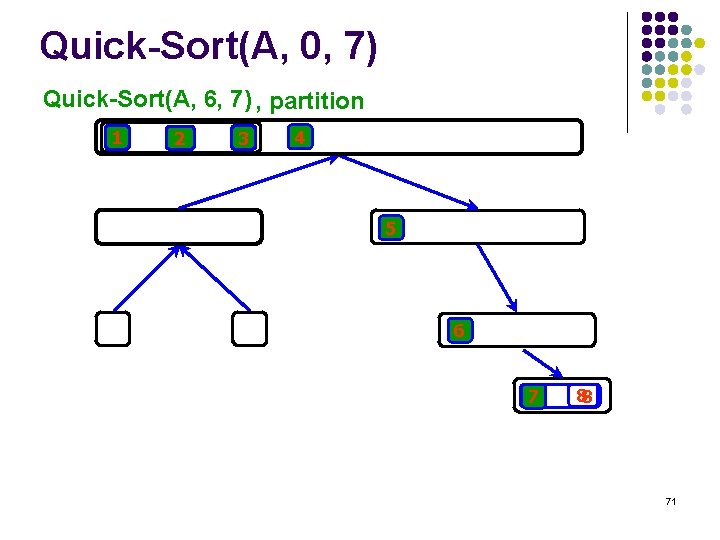
Quick-Sort(A, 0, 7) Quick-Sort(A, 6, 7) , partition 1 2 3 4 5 6 7 88 71

Quick-Sort(A, 0, 7) returncase Quick-Sort(A, 7, 7) , base 1 2 3 4 5 6 7 8 8 72

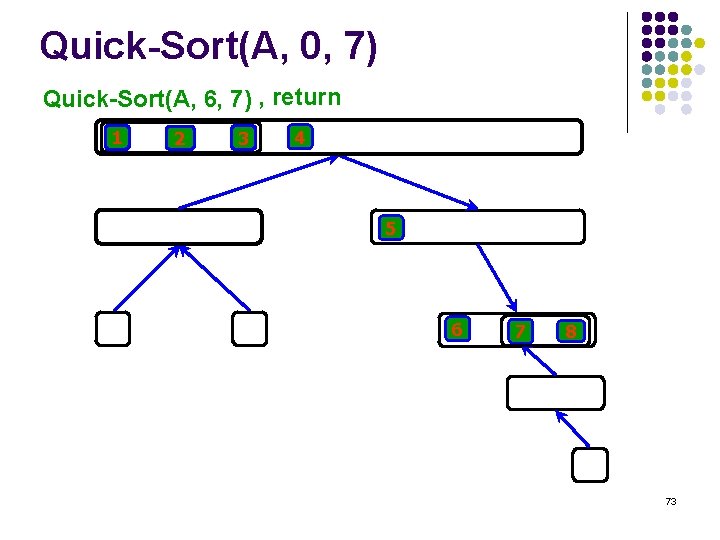
Quick-Sort(A, 0, 7) Quick-Sort(A, 6, 7) , return 1 2 3 4 5 6 7 8 73

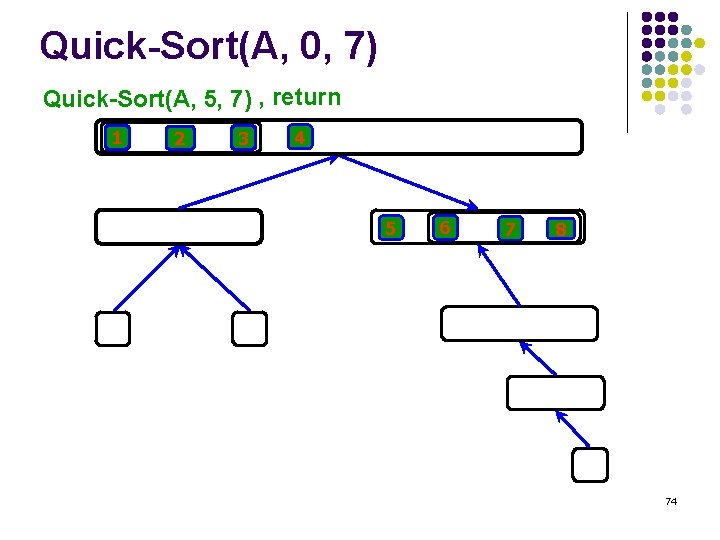
Quick-Sort(A, 0, 7) Quick-Sort(A, 5, 7) , return 1 2 3 4 5 6 7 8 74

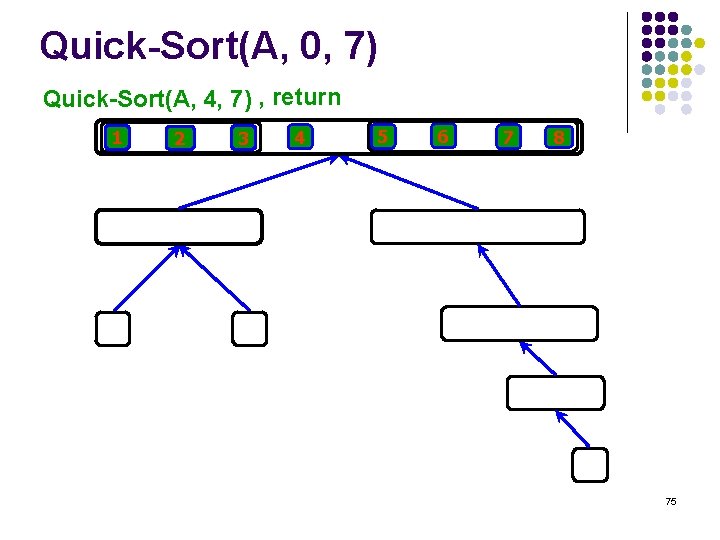
Quick-Sort(A, 0, 7) Quick-Sort(A, 4, 7) , return 1 2 3 4 5 6 7 8 75

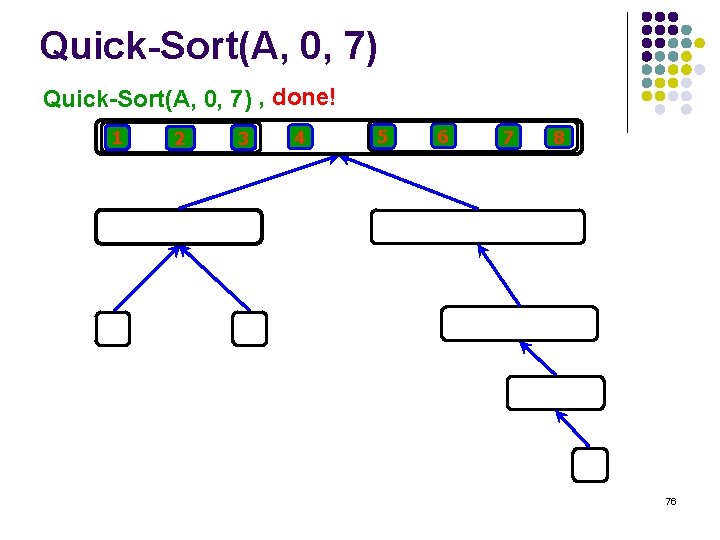
Quick-Sort(A, 0, 7) , done! 1 2 3 4 5 6 7 8 76

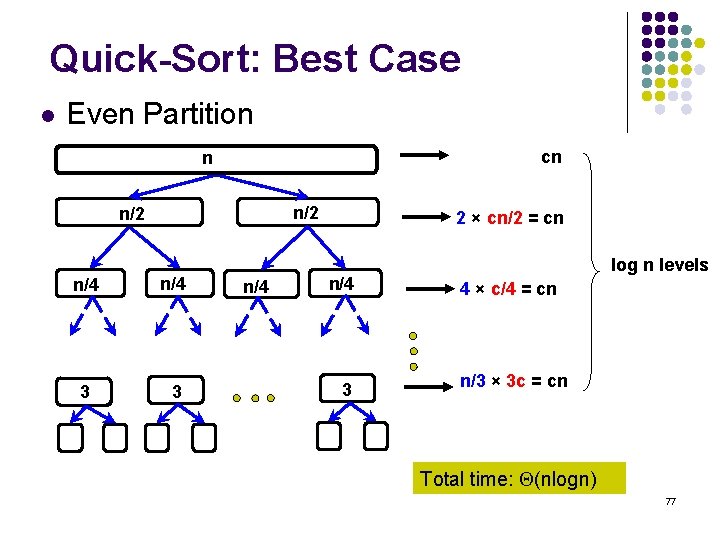
Quick-Sort: Best Case l Even Partition cn n n/2 n/4 3 3 n/4 2 × cn/2 = cn n/4 3 log n levels 4 × c/4 = cn n/3 × 3 c = cn Total time: (nlogn) 77

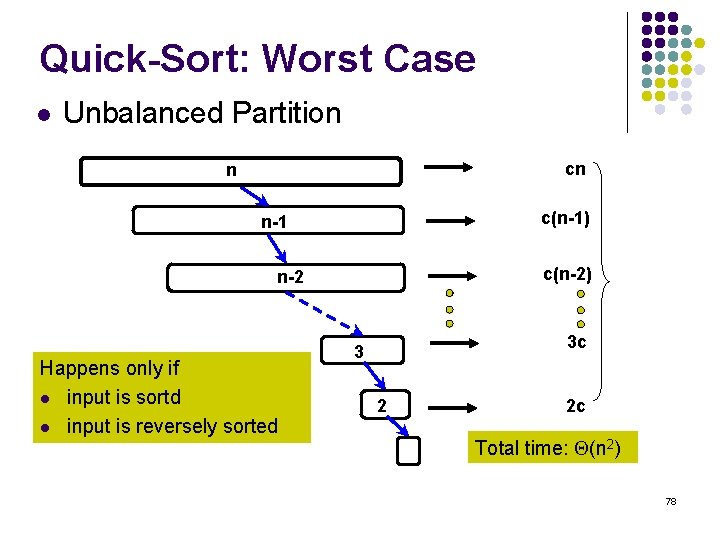
Quick-Sort: Worst Case l Unbalanced Partition cn n c(n-1) n-1 c(n-2) n-2 Happens only if l input is sortd l input is reversely sorted 3 c 3 2 2 c Total time: (n 2) 78

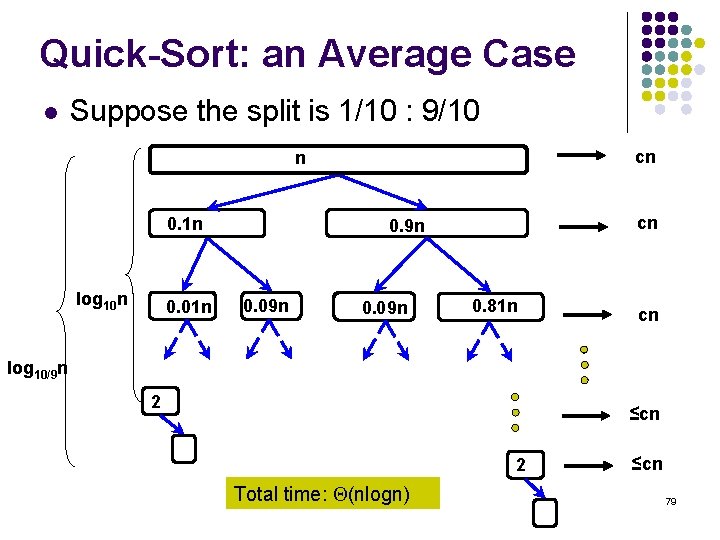
Quick-Sort: an Average Case l Suppose the split is 1/10 : 9/10 cn n 0. 1 n log 10 n 0. 01 n cn 0. 9 n 0. 09 n 0. 81 n cn log 10/9 n 2 ≤cn 2 Total time: (nlogn) ≤cn 79

Quick-Sort Summary l Time l l l Most of the work done in partitioning. Average case takes (n log(n)) time. Worst case takes (n 2) time Space l Sorts in-place, i. e. , does not require additional space 80

Summary l Divide and Conquer l Merge-Sort l l Most of the work done in Merging (n log(n)) time (n) space Quick-Sort l l Most of the work done in partitioning Average case takes (n log(n)) time Worst case takes (n 2) time (1) space 81

Homework 1. What is the running time of Merge-Sort if the array is already sorted? What is the best case running time of Merge-Sort? 2. Demonstrate the working of Partition on sequence (13, 5, 14, 11, 16, 12, 1, 15). What is the value of i returned at the completion of Partition? 82