Comparing algorithms Quick sort Heap sort Selection sort

Comparing algorithms (Quick sort, Heap sort, Selection sort) Student: Blaž Mahnič Course: Programming, data structures and algorithms Supervisor: doc. dr. Anton Biasizzo

Agenda • • • Introduction Quick sort Heap sort Selection sort Performance tests Conclusion

Introduction • Sorting algorithm? • Sorting is important for optimizing the use of other algorithms (search and merge) • Bubble Sort was analyzed in 1956 • Library Sort was first published in 2004.

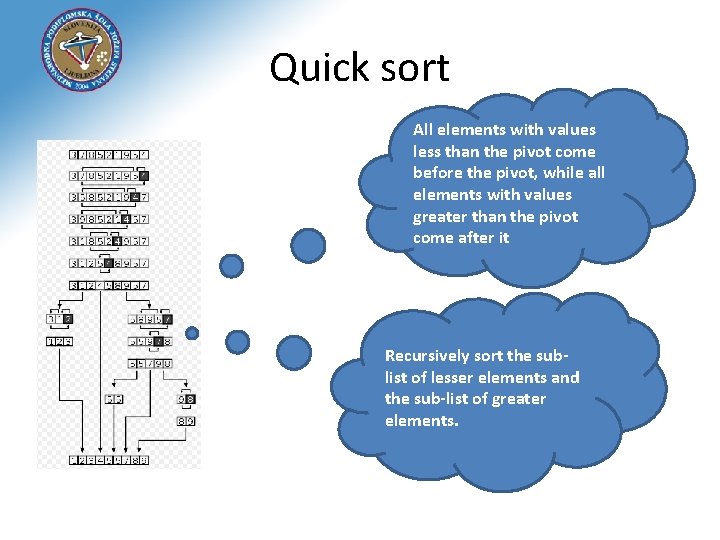
Quick sort • Developed in 1960 by Tony Hoare, he developed the algorithm in order to sort the words to be translated • Is a divide and conquer algorithm Pick an element, called a pivot, from the list

Quick sort All elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it Recursively sort the sublist of lesser elements and the sub-list of greater elements.

Quick sort - Implementation issues • Choice of pivot – In early versions the leftmost element was choosen, this causes worst-case behavior on already sorted arrays – SOLUTION: random index for the pivot, middle index of the partition, the median of the first, middle and last element of the partition

Quick sort - Improvement • Use insertion sort, which has a smaller constant factor and is thus faster on small arrays • The improvement is implemented in the TEST section

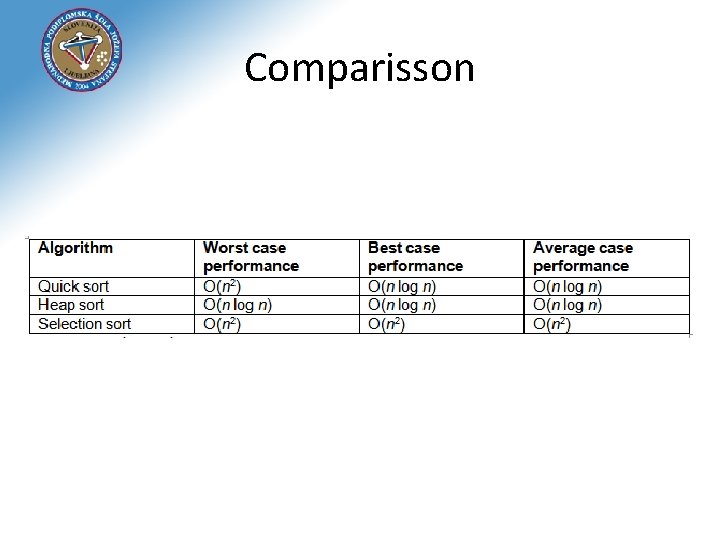
Heap sort • Invented by J. R. J. Williams • Is a comparison-based sorting algorithm, and is part of the selection sort family • It has the advantage of a more favorable worst -case O(nlog n) runtime in comparisson with quick sort • an in-place algorithm, but is not a stable sort

Heap sort - steps HEAP: if B is a child node of A, then key(A) ≥ key(B). This implies that an element with the greatest key is always in the root node. - Removes the largest item and place it at the end of the partially sorted array - After removing the largest item, it reconstructs the heap, removes the largest remaining item -This is repeated until there are no items left in the heap and the sorted array is full

Selection sort • An in-place comparison sort • O(n 2) time complexity, making it inefficient on large lists • It has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.

Selection sort - steps • Find the minimum value in the list • Swap it with the value in the first position • Repeat the steps above for the remainder of the list (starting at the second position and advancing each time)

Comparisson

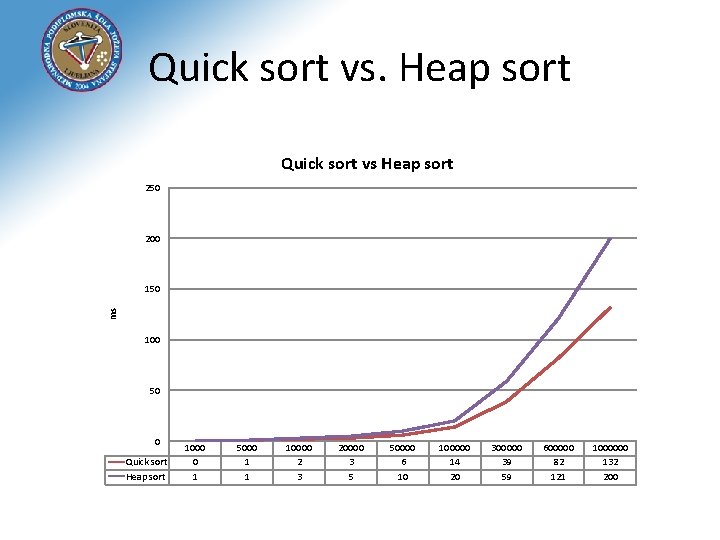
Quick sort vs. Heap sort Quick sort vs Heap sort 250 200 ms 150 100 50 0 Quick sort Heap sort 1000 0 1 5000 1 1 10000 2 3 20000 3 5 50000 6 10 100000 14 20 300000 39 59 600000 82 121 1000000 132 200

Quick sort vs. Heap sort • Heap sort is slower in practice, but it has the advantage of a more favorable worst-case O(nlog n) runtime • Quicksort has better locality of reference - the next thing to be accessed is usually close in memory to the thing you just looked at • Things that are close together will likely be cached together, so quicksort tends to be faster • Quicksort's worst-case performance is significantly worse than heapsort's is • Critical applications will require guarantees of speed performance, heapsort is the right way to go for such cases

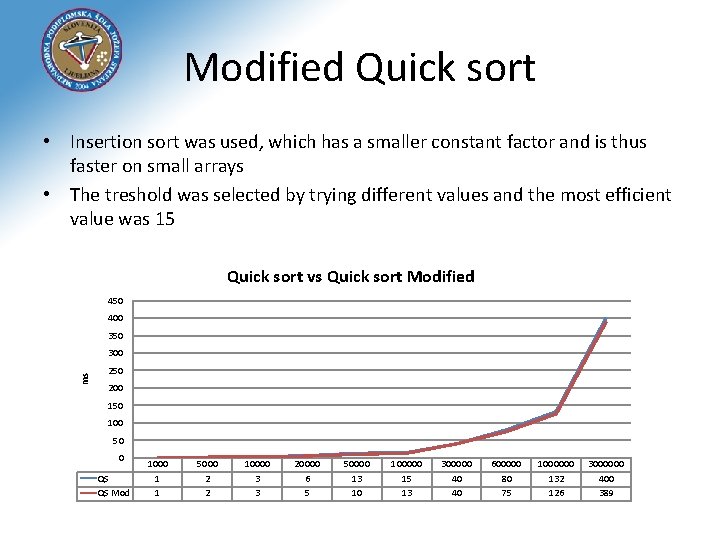
Modified Quick sort • Insertion sort was used, which has a smaller constant factor and is thus faster on small arrays • The treshold was selected by trying different values and the most efficient value was 15 Quick sort vs Quick sort Modified 450 400 350 ms 300 250 200 150 100 50 0 QS QS Mod 1000 1 1 5000 2 2 10000 3 3 20000 6 5 50000 13 10 100000 15 13 300000 40 40 600000 80 75 1000000 132 126 3000000 400 389

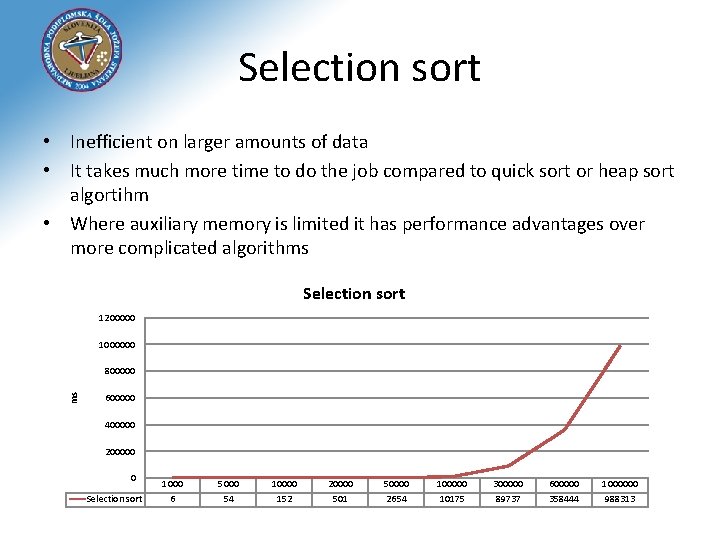
Selection sort • Inefficient on larger amounts of data • It takes much more time to do the job compared to quick sort or heap sort algortihm • Where auxiliary memory is limited it has performance advantages over more complicated algorithms Selection sort 1200000 1000000 ms 800000 600000 400000 200000 0 Selection sort 1000 6 5000 54 10000 152 20000 501 50000 2654 100000 10175 300000 89737 600000 358444 1000000 988313

Conclusion • Quick sort should never be used in applications which require a guarantee of response time, unless it is treated as an O(n 2) algorithm • If you have to assume O(n 2) time, then - if n is small, you're better off using selection sort • If n is large, you should obviously be using heap sort, for its guaranteed O(nlog n) time • Life-critical and mission-critical applications will generally have a response time as part of the system specifications In all such systems, it is not acceptable to design based on average performance, you must always allow for the worst case, and thus treat quicksort as O(n 2).