HEAP SORT HEAP SORT A sorting algorithm that

HEAP SORT

HEAP SORT A sorting algorithm that works by first organizing the data to be sorted into a special type of binary tree called a heap

DEFINITION Max Heap Store data in ascending order Has property of A[Parent(i)] ≥ A[i] Min Heap Store data in descending order Has property of A[Parent(i)] ≤ A[i] • But we can use both max heap and min heap for ascending as well as descending

HEAP SORT ALGORITHM • • • Heap Sort Algorithm for sorting in increasing order: Finally, heapify the root of tree. Build a max heap from the input data. At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of heap by Repeat above steps until size of heap is greater than 1.

1. BUILD-MAX-HEAP(A) 2. for i ← length[A] downto 2 3. do exchange A[1] ↔ A[i] 4. MAX-HEAPIFY(A, 1, i - 1) Running time: O(nlogn) --- Can be shown to be Θ(nlogn) O(n) n-1 times O(logn)

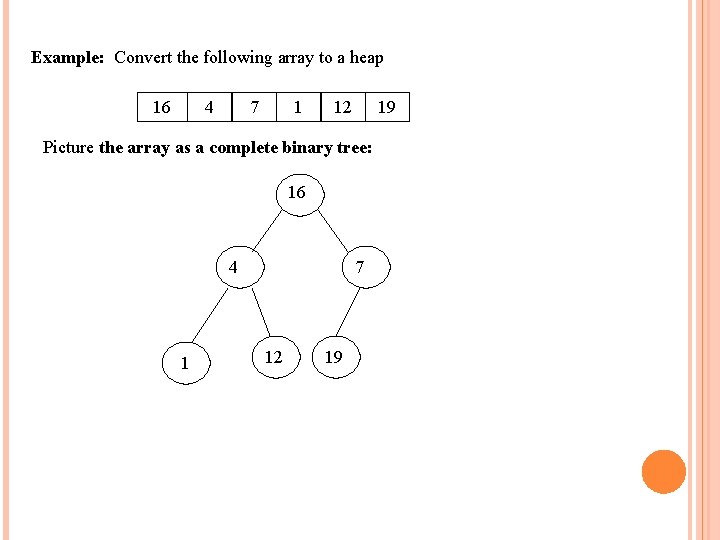
Example: Convert the following array to a heap 16 4 7 1 12 19 Picture the array as a complete binary tree: 16 4 1 7 12 19

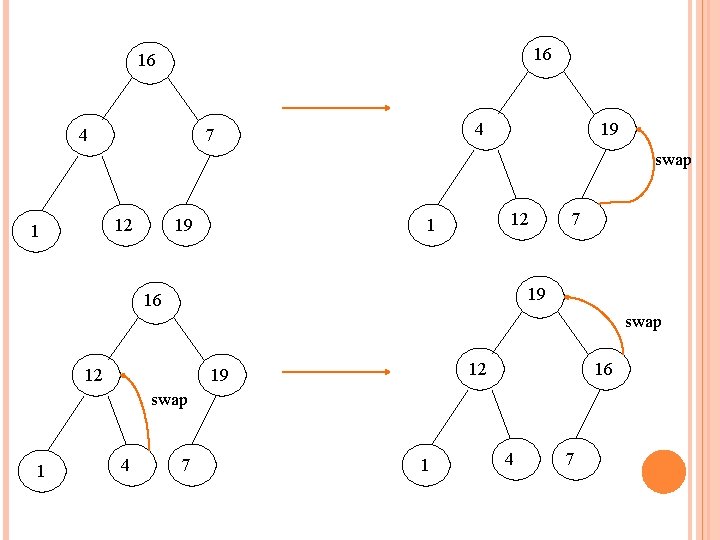
16 16 4 4 7 19 swap 12 1 19 12 1 7 19 16 swap 12 12 19 16 swap 1 4 7

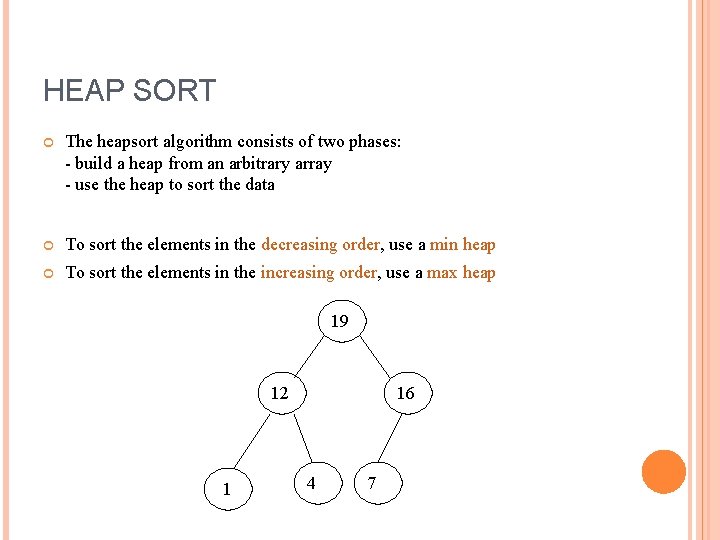
HEAP SORT The heapsort algorithm consists of two phases: - build a heap from an arbitrary array - use the heap to sort the data To sort the elements in the decreasing order, use a min heap To sort the elements in the increasing order, use a max heap 19 12 1 16 4 7

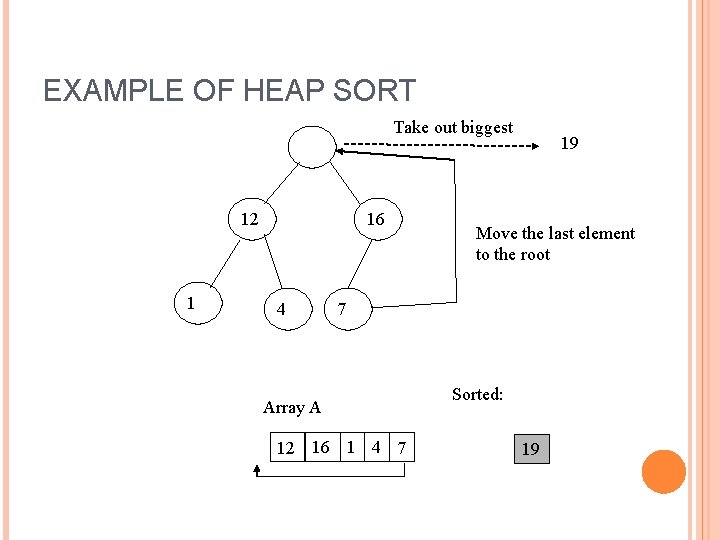
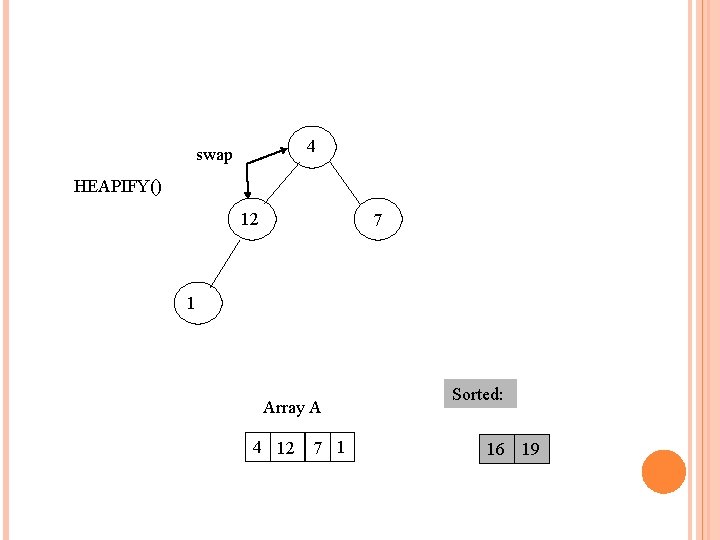
EXAMPLE OF HEAP SORT Take out biggest 12 1 16 4 19 Move the last element to the root 7 Array A 12 16 1 4 7 Sorted: 19

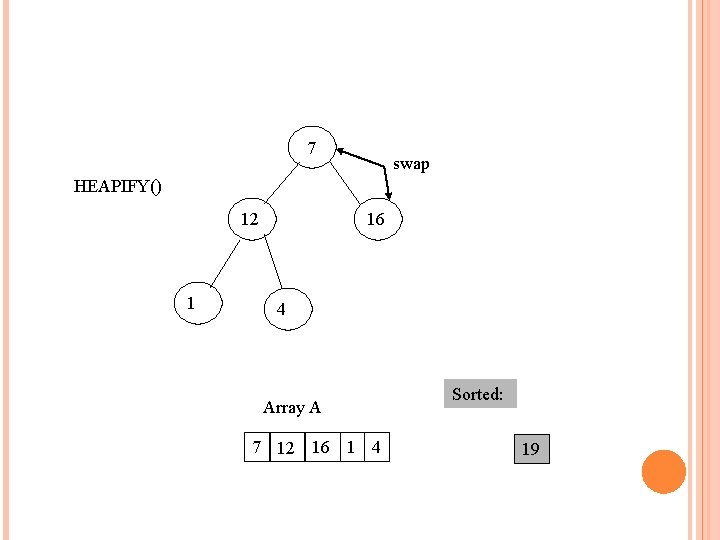
7 swap HEAPIFY() 12 1 16 4 Array A 7 12 16 1 4 Sorted: 19

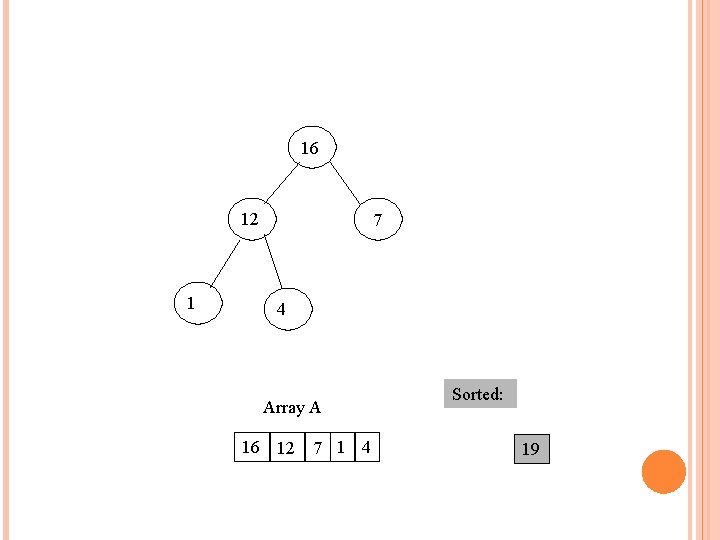
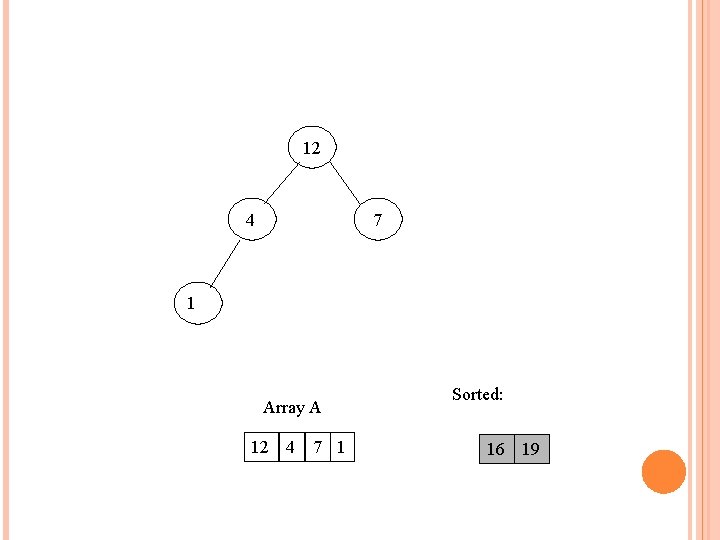
16 12 1 7 4 Array A 16 12 7 1 4 Sorted: 19

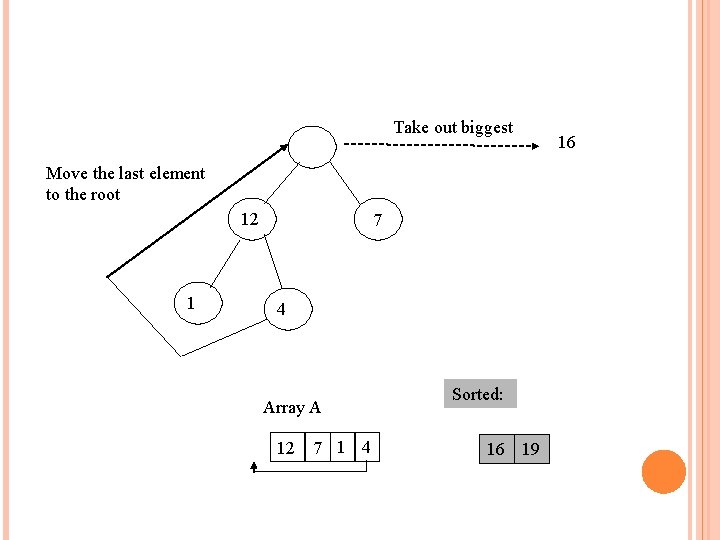
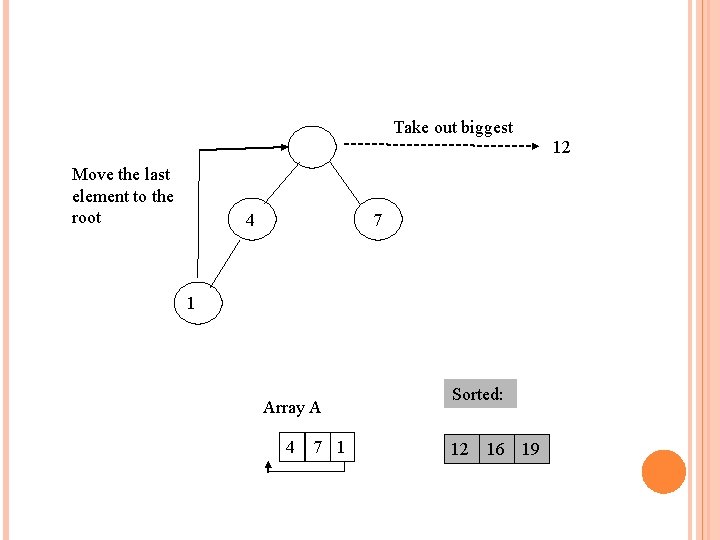
Take out biggest Move the last element to the root 12 1 7 4 Array A 12 7 1 4 Sorted: 16 19 16

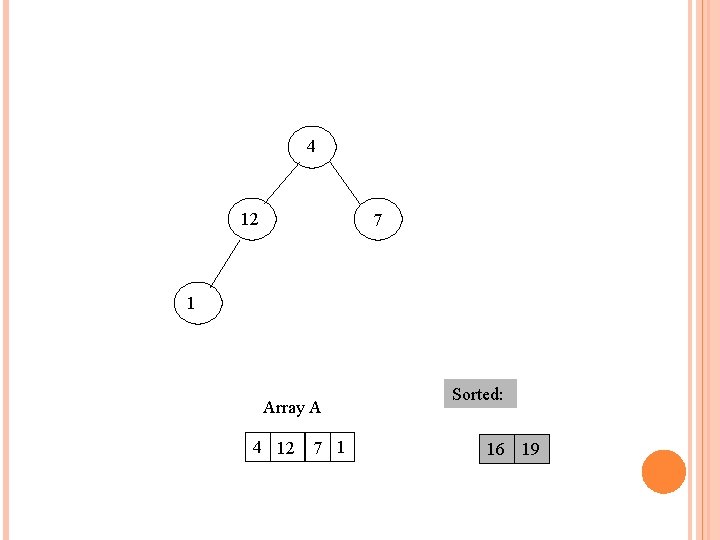
4 12 7 1 Array A 4 12 7 1 Sorted: 16 19

4 swap HEAPIFY() 12 7 1 Array A 4 12 7 1 Sorted: 16 19

12 7 4 1 Array A 12 4 7 1 Sorted: 16 19

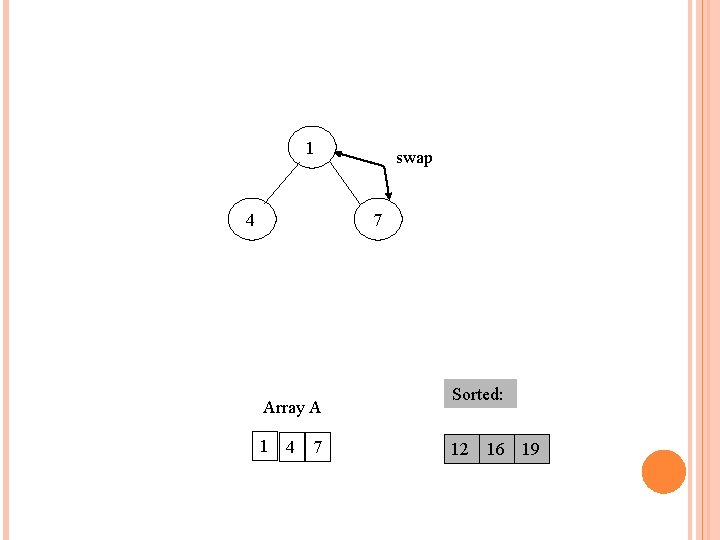
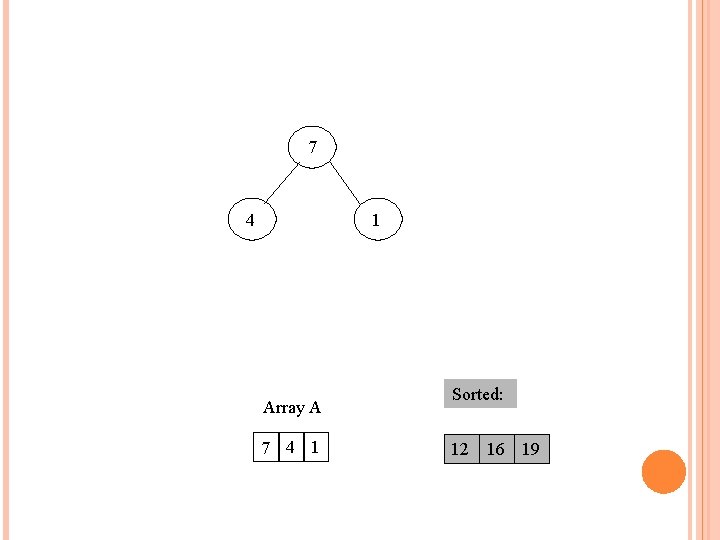
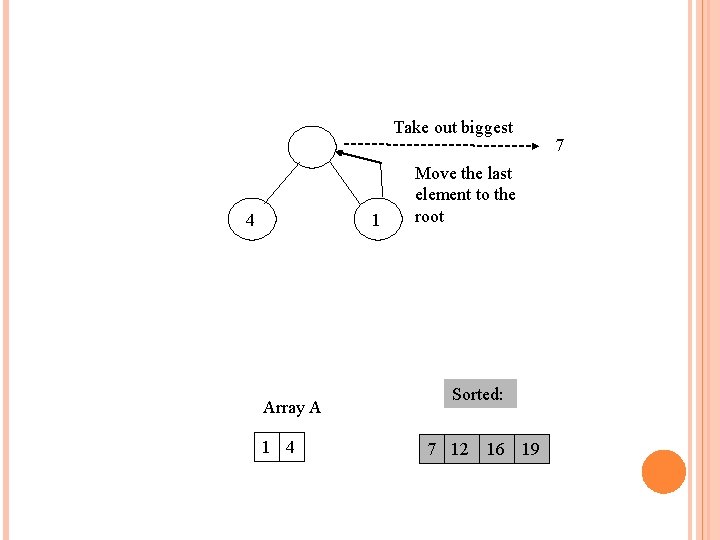
Take out biggest Move the last element to the root 7 4 1 Array A 4 7 1 Sorted: 12 16 19 12

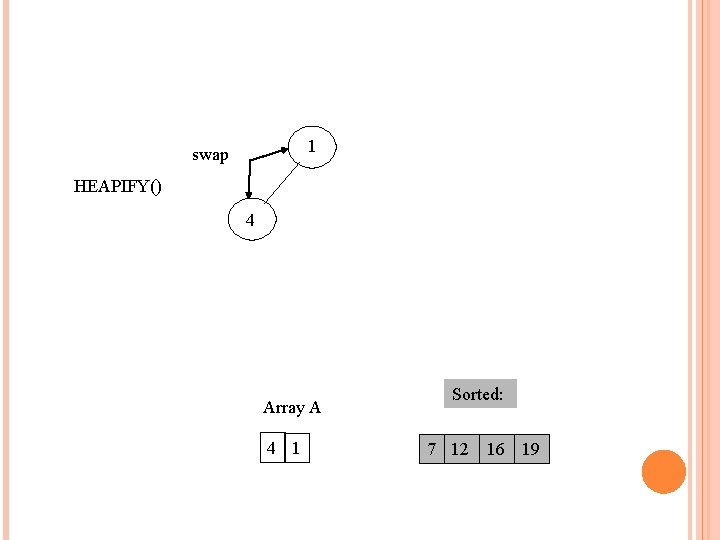
1 swap 7 4 Array A 1 4 7 Sorted: 12 16 19

7 4 1 Array A 7 4 1 Sorted: 12 16 19

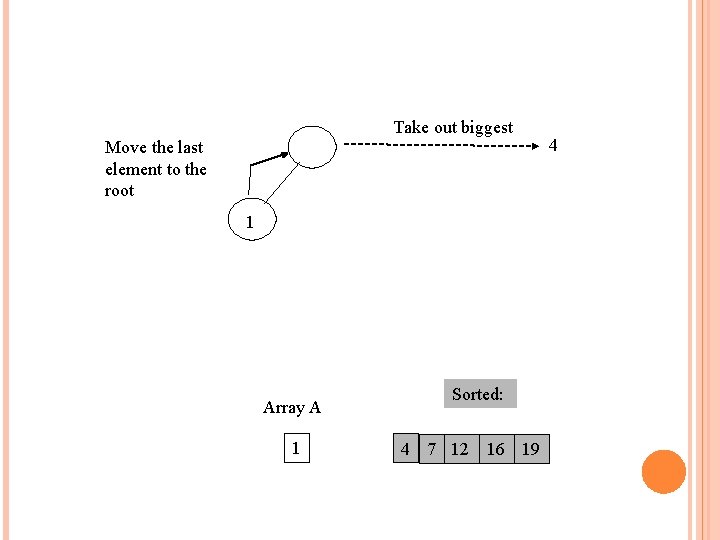
Take out biggest 4 1 Array A 1 4 Move the last element to the root Sorted: 7 12 16 19 7

1 swap HEAPIFY() 4 Array A 4 1 Sorted: 7 12 16 19

Take out biggest Move the last element to the root 1 Array A 1 Sorted: 4 7 12 16 19 4

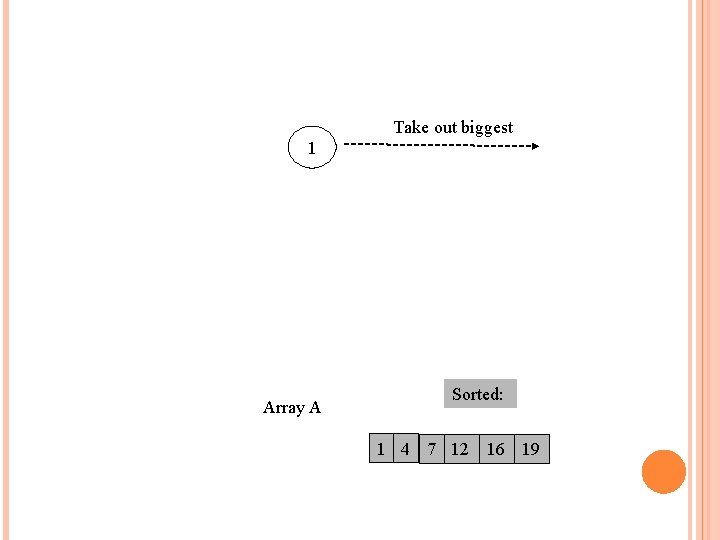
Take out biggest 1 Array A Sorted: 1 4 7 12 16 19

Sorted: 1 4 7 12 16 19

TIME ANALYSIS Build Heap Algorithm will run in O(n) time There are n-1 calls to Heapify each call requires O(log n) time Heap sort program combine Build Heap program and Heapify, therefore it has the running time of O(n log n) time Total time complexity: O(n log n)

THANK YOU