Data Structures Algorithms Priority Queues Heap Sort Heap











![Bottom-up Heapify template <class Item> void bubble. Up(Item a[], int k) { while (k Bottom-up Heapify template <class Item> void bubble. Up(Item a[], int k) { while (k](https://slidetodoc.com/presentation_image_h/7ba85b4b26ef9246a93aa8cdbda9ac4d/image-20.jpg)
![Top-down Heapify template <class Item> void sift. Down(Item a[], int k, int N) { Top-down Heapify template <class Item> void sift. Down(Item a[], int k, int N) {](https://slidetodoc.com/presentation_image_h/7ba85b4b26ef9246a93aa8cdbda9ac4d/image-31.jpg)


![Priority Queue Sort template <class Item> void PQsort(Item a[], int l, int r) { Priority Queue Sort template <class Item> void PQsort(Item a[], int l, int r) {](https://slidetodoc.com/presentation_image_h/7ba85b4b26ef9246a93aa8cdbda9ac4d/image-34.jpg)


![Heap. Sort template <class Item> void heap. Sort(Item a[], int l, int r) { Heap. Sort template <class Item> void heap. Sort(Item a[], int l, int r) {](https://slidetodoc.com/presentation_image_h/7ba85b4b26ef9246a93aa8cdbda9ac4d/image-37.jpg)




- Slides: 41

Data Structures & Algorithms Priority Queues & Heap. Sort

Heap. Sort & Priority Queues Often need to insert and remove items dynamically • Priority queues for scheduling • Event-based simulations • Numerical computations Desired: • Work in-place • Fast sorting (N lg N time) • Support fast insertion • Support fast removal of largest item

Priority Queues • Defn. 9. 1: A priority queue is a data structure of items with keys that supports two basic operations: • insert a new item, and • remove the item with the largest key. • Can use a priority queue to sort by • inserting all items, • then removing all items.

Priority Queue ADT Basic interface: template <class Item> class PQ { private: // implementation-dependent code public: PQ(int); int empty() const; void insert(Item); Item getmax(); };

Priority Queues May want to support many other operations: • Construct a priority queue from N items • Insert a new item • Remove the maximum item • Change the priority (key) of an item • Remove an arbitrary item • Join two priority queues into one

Priority Queue Basic implementations: 1 – quick insert/slow remove • Add item to unordered list/array • Remove max by searching list, swap with last item (no holes) 2 – slow insert/fast remove • Add item to ordered list/array • Remove max by removing last item

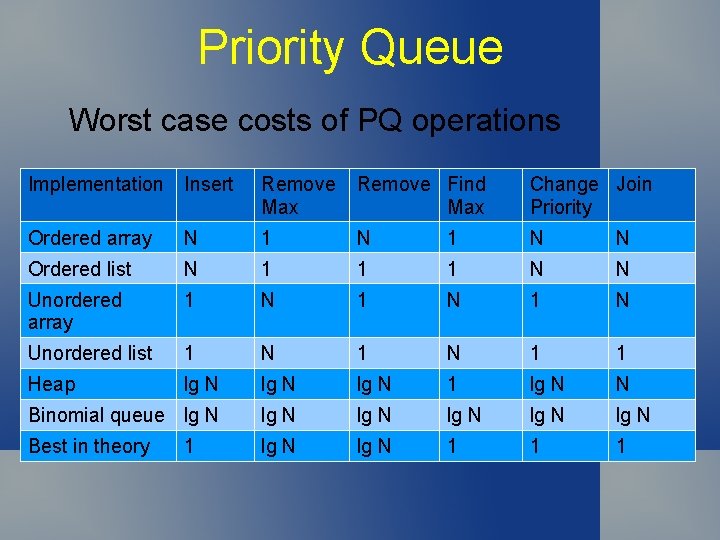
Priority Queue Worst case costs of PQ operations Implementation Insert Remove Max Remove Find Max Change Join Priority Ordered array N 1 N N Ordered list N 1 1 1 N N Unordered array 1 N 1 N Unordered list 1 N 1 1 Heap lg N 1 lg N N Binomial queue lg N lg N Best in theory lg N 1 1

Heap Defn 9. 2: A tree is heap-ordered if the key in each node is less than or equal to the key in the node's parent (if any). Property 9. 1: No node in a heap-ordered tree has a key larger than the root

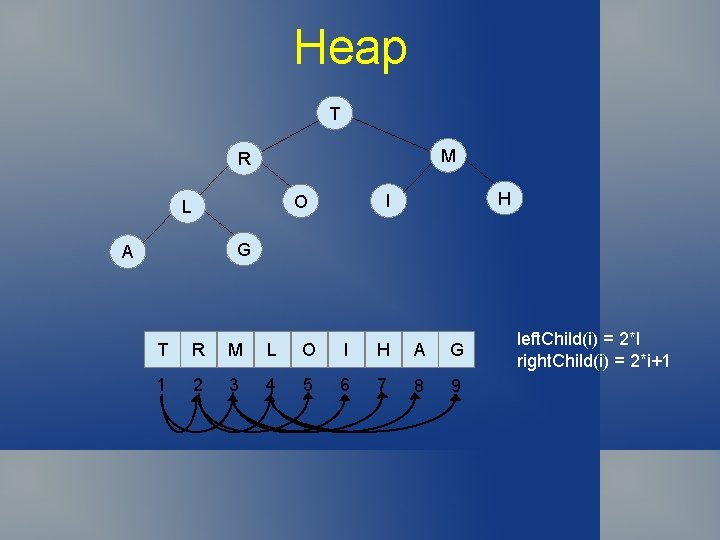
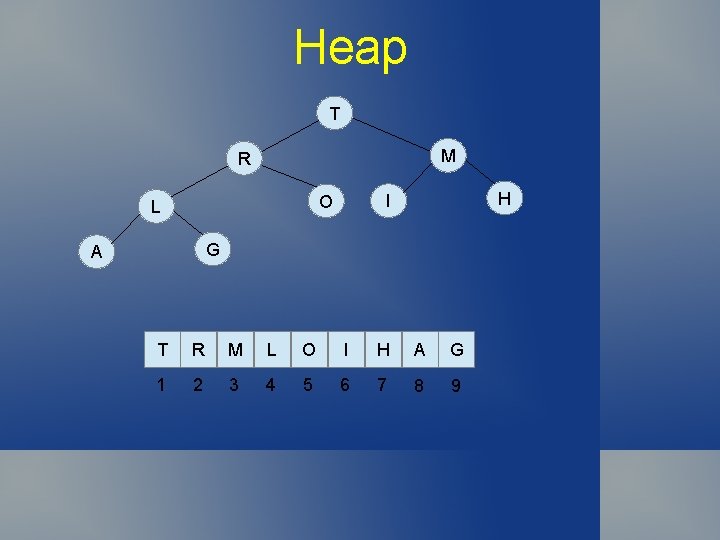
Heap Very convenient to use a complete binary tree (tree filled level order left to right). Complete binary tree easy to represent in array with root in a[1], its children at a[2] and a[3], … a[i]'s at a[2 i] and a[2 i+1] Defn 9. 3: A heap is a set of nodes arranged in a complete heap-ordered tree, represented as an array.

Heap T M R H I O L G A T R M L O I H A G 1 2 3 4 5 6 7 8 9 left. Child(i) = 2*I right. Child(i) = 2*i+1

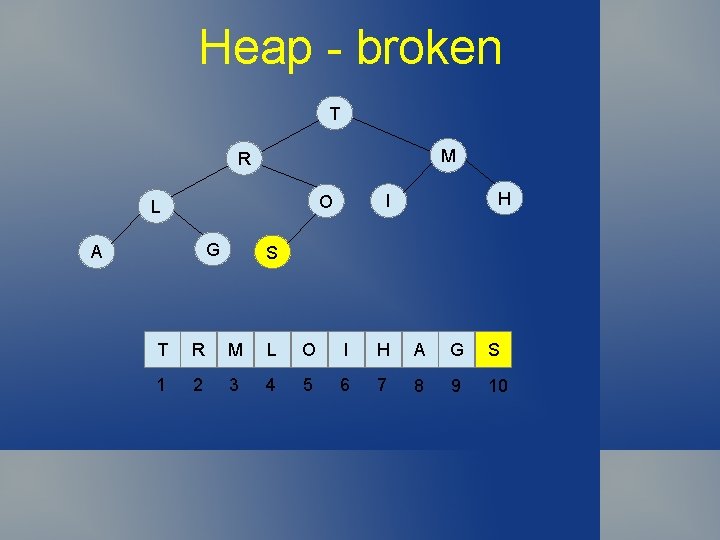
Heapify Making an array interpreted as a complete binary tree become heapordered. If start with heap, and make a modification that could violate the heap property, then heapify to fix heap.

Heapify If priority of a node is increased, or new node is added at bottom (end of array), must travel up until node is in right place. If priority of a node is decreased, or replace root with another node, then must travel down the heap until suitable place is found.

Heap T M R H I O L G A T R M L O I H A G 1 2 3 4 5 6 7 8 9

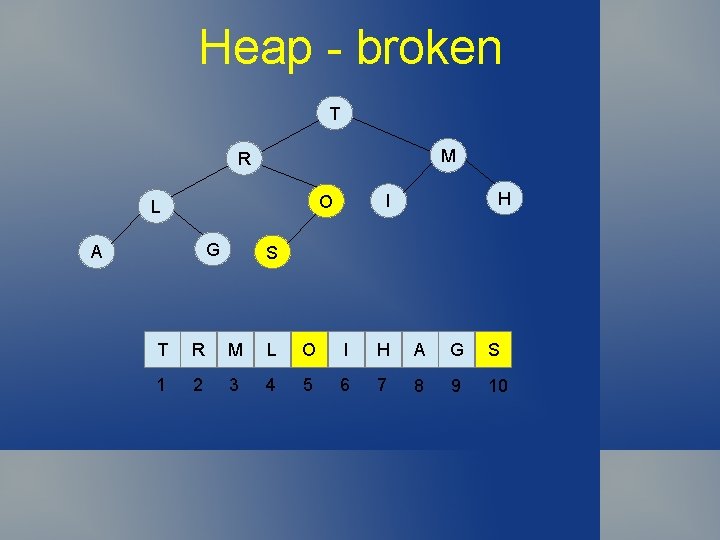
Heap - broken T M R G A H I O L S T R M L O I H A G S 1 2 3 4 5 6 7 8 9 10

Heap - broken T M R G A H I O L S T R M L O I H A G S 1 2 3 4 5 6 7 8 9 10

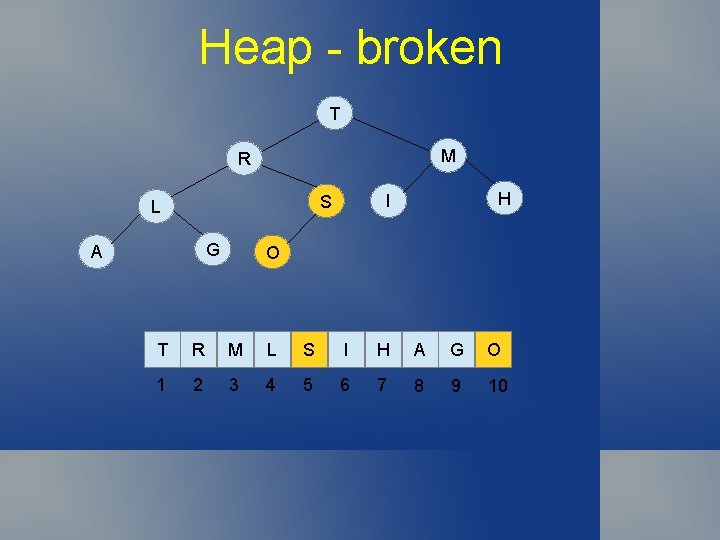
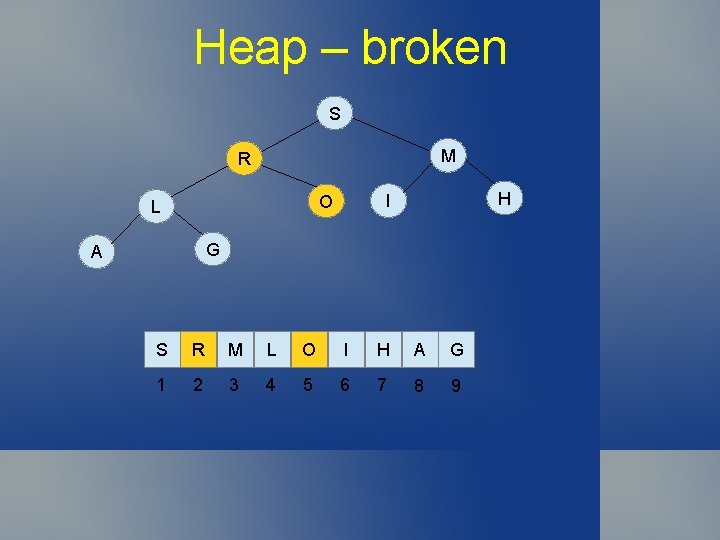
Heap - broken T M R G A H I S L O T R M L S I H A G O 1 2 3 4 5 6 7 8 9 10

Heap - broken T M R G A H I S L O T R M L S I H A G O 1 2 3 4 5 6 7 8 9 10

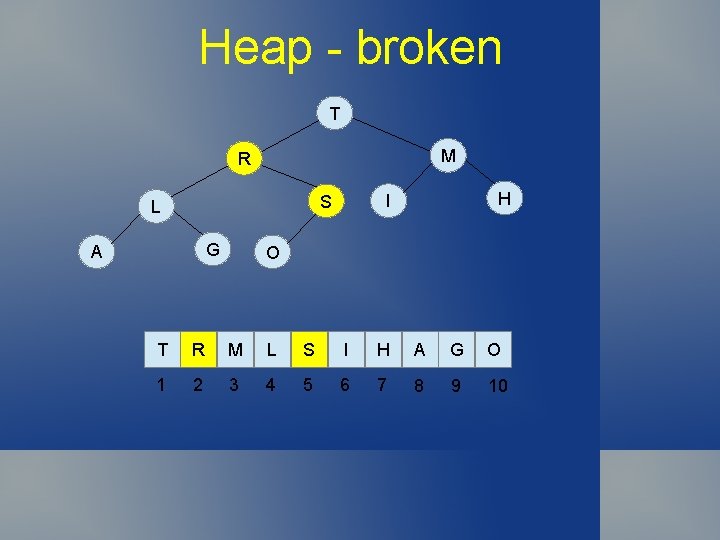
Heap - broken T M S G A H I R L O T S M L R I H A G O 1 2 3 4 5 6 7 8 9 10

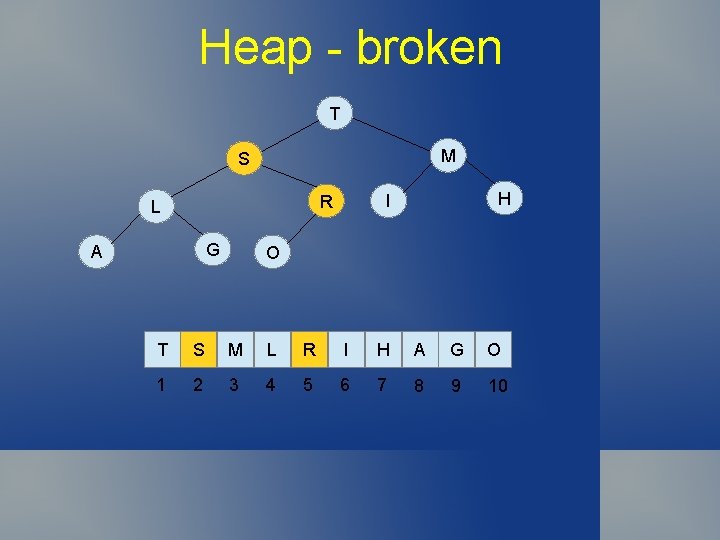
Heap - fixed T M S G A H I R L O T S M L R I H A G O 1 2 3 4 5 6 7 8 9 10
![Bottomup Heapify template class Item void bubble UpItem a int k while k Bottom-up Heapify template <class Item> void bubble. Up(Item a[], int k) { while (k](https://slidetodoc.com/presentation_image_h/7ba85b4b26ef9246a93aa8cdbda9ac4d/image-20.jpg)
Bottom-up Heapify template <class Item> void bubble. Up(Item a[], int k) { while (k > 1 && a[k/2] < a[k]) { exch(a[k], a[k/2]); k /= 2; } }

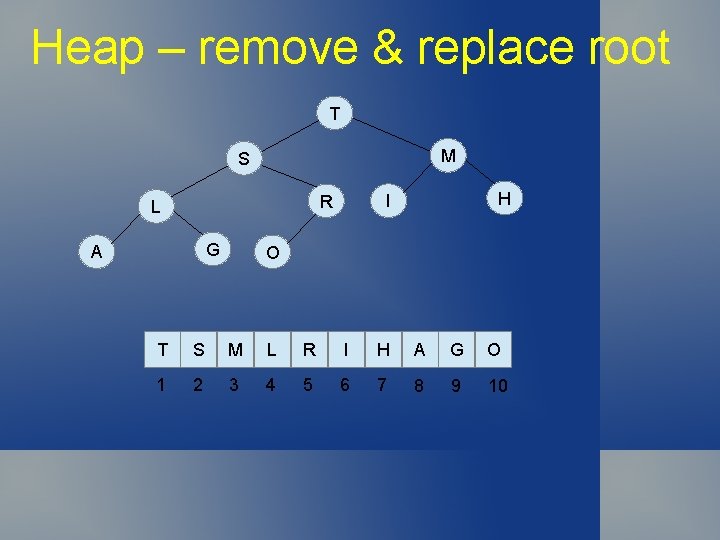
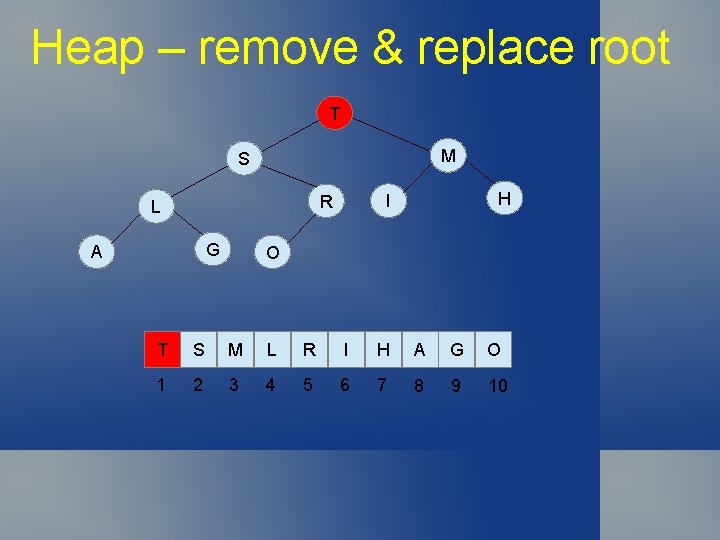
Heap – remove & replace root T M S G A H I R L O T S M L R I H A G O 1 2 3 4 5 6 7 8 9 10

Heap – remove & replace root T M S G A H I R L O T S M L R I H A G O 1 2 3 4 5 6 7 8 9 10

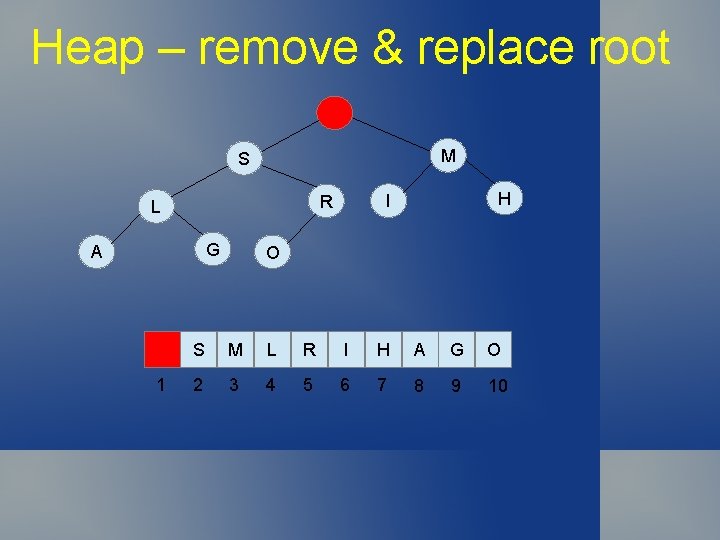
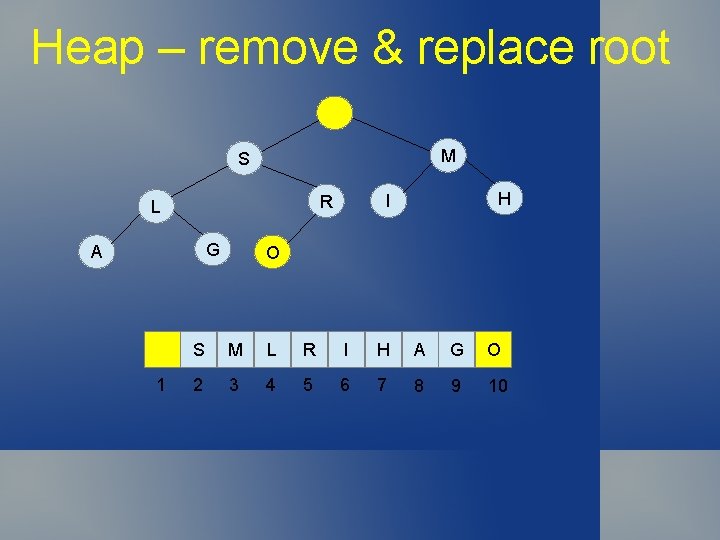
Heap – remove & replace root M S G A 1 H I R L O S M L R I H A G O 2 3 4 5 6 7 8 9 10

Heap – remove & replace root M S G A 1 H I R L O S M L R I H A G O 2 3 4 5 6 7 8 9 10

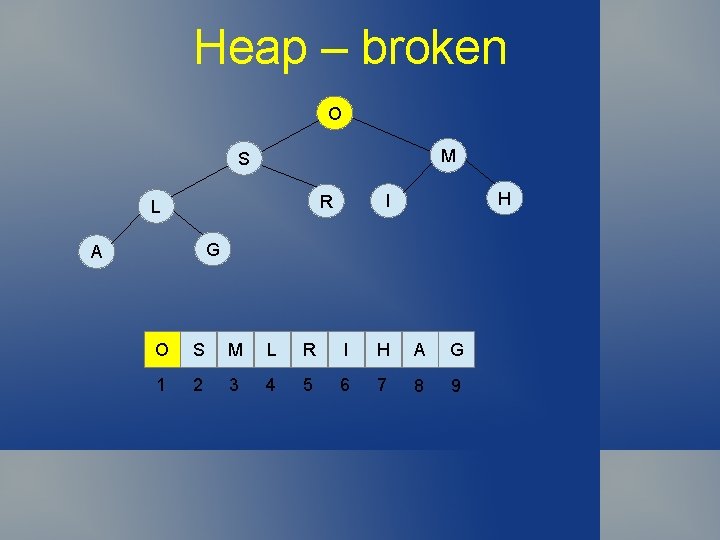
Heap – broken O M S H I R L G A O S M L R I H A G 1 2 3 4 5 6 7 8 9

Heap – broken O M S H I R L G A O S M L R I H A G 1 2 3 4 5 6 7 8 9

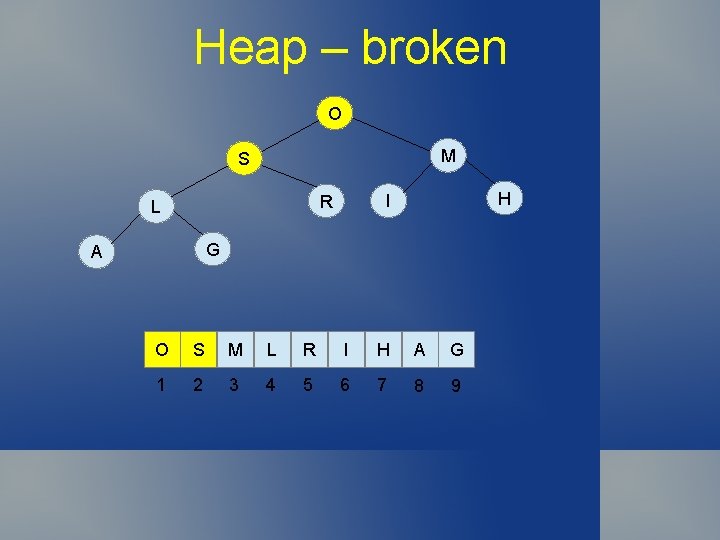
Heap – broken S M O H I R L G A S O M L R I H A G 1 2 3 4 5 6 7 8 9

Heap – broken S M O H I R L G A S O M L R I H A G 1 2 3 4 5 6 7 8 9

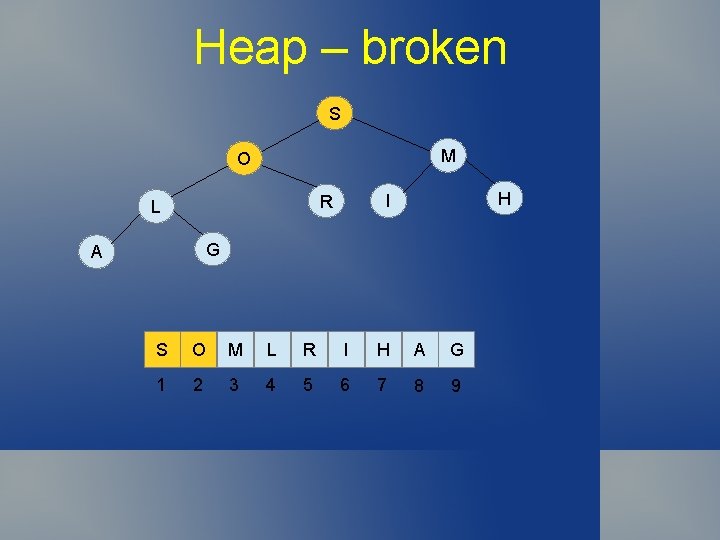
Heap – broken S M R H I O L G A S R M L O I H A G 1 2 3 4 5 6 7 8 9

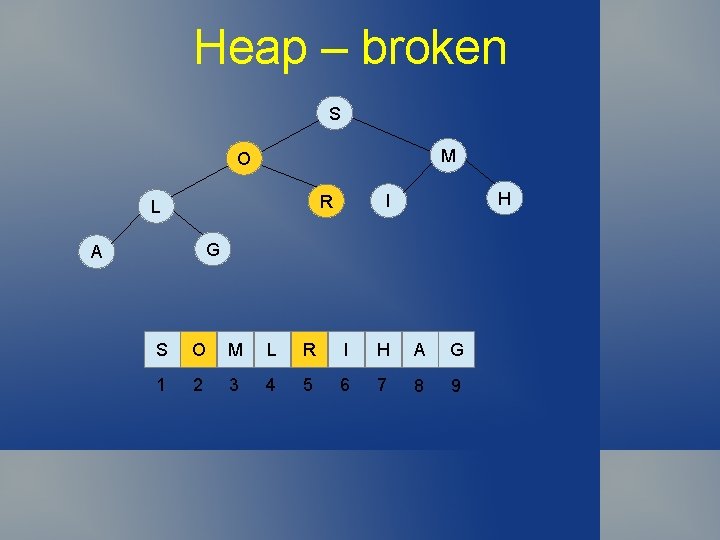
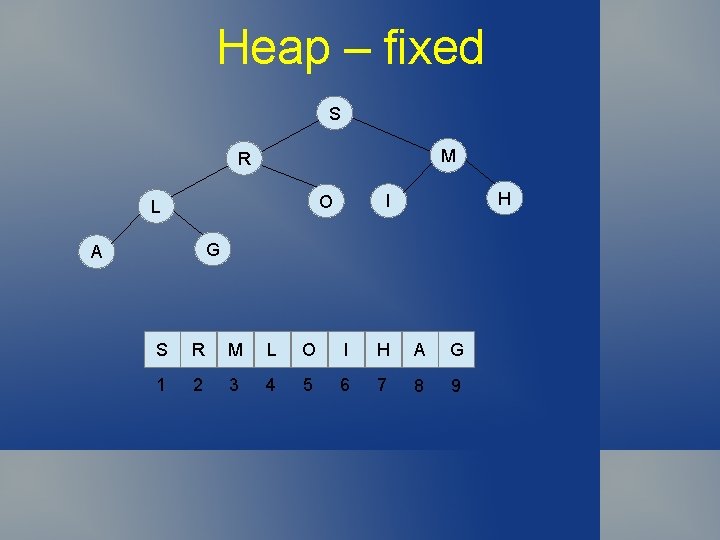
Heap – fixed S M R H I O L G A S R M L O I H A G 1 2 3 4 5 6 7 8 9
![Topdown Heapify template class Item void sift DownItem a int k int N Top-down Heapify template <class Item> void sift. Down(Item a[], int k, int N) {](https://slidetodoc.com/presentation_image_h/7ba85b4b26ef9246a93aa8cdbda9ac4d/image-31.jpg)
Top-down Heapify template <class Item> void sift. Down(Item a[], int k, int N) { while (2*k <= N) { int j *= 2; // left child // pick larger child if (j < N && a[j] < a[j+1]) ++j; // if out of place, . . . if (!(a[k] < a[j])) break; // swap with larger child exch(a[k], a[j]); k = j; } }

Priority Queue So, implement insert by appending new item to end of array (bottom of tree), then bubbling up. Implement remove max by removing root item (first item in array) and moving last item to root, then sifting down. Each of these operations take at most O(lg N) time (maximum path length in complete binary tree).

Priority Queue The change priority, remove arbitrary node, and replace the maximum operations all take O(lg N) time in a heap. Sort by inserting, then removing items from largest to smallest. Note that joining two heaps is not mentioned here – a bit harder to do.
![Priority Queue Sort template class Item void PQsortItem a int l int r Priority Queue Sort template <class Item> void PQsort(Item a[], int l, int r) {](https://slidetodoc.com/presentation_image_h/7ba85b4b26ef9246a93aa8cdbda9ac4d/image-34.jpg)
Priority Queue Sort template <class Item> void PQsort(Item a[], int l, int r) { int k; PQ<Item> pq(r-l+1); // make priority queue for (k = l; k <= r; ++k) pq. insert(a[k]); // insert all items for (k = r; k > 0; --k) // in decreasing order a[k] = pq. getmax(); // copy back to a[] }

Heap. Sort If already have unordered array, can put into heap order faster than N lg N time. Rather than do N insertions, just sift down starting at next to bottom level. Each of these operations starts with two sub-heaps and a root that may be out of place, and makes a bigger sub-heap. This is bottom-up heap construction.

Heap. Sort Property 9. 4: Bottom-up heap construction takes linear time. Prf: For a tree of size N = 2 n – 1, we have 2 n-2 sub-heaps of size 3, which may need one promotion; 2 n-3 sub-heaps of size 7 which may need two promotions, etc. The maximum number of promotions is Sum k 2 n-k-1 = 2 n – 1 < N. Proof is similar when N+1 is not 2 n
![Heap Sort template class Item void heap SortItem a int l int r Heap. Sort template <class Item> void heap. Sort(Item a[], int l, int r) {](https://slidetodoc.com/presentation_image_h/7ba85b4b26ef9246a93aa8cdbda9ac4d/image-37.jpg)
Heap. Sort template <class Item> void heap. Sort(Item a[], int l, int r) { int k, N = r-l+1; Item *pq = a+l-1; // make part of a[] PQ for (k = N/2; k > 0; --k) sift. Down(pq, k, N); // bottom-up heapify while (N > 1) // in decreasing order { exch(pq[1], pq[N]); // largest to end sift. Down(pq, 1, --N); // fix heap } }

Heap. Sort Property 9. 5: Heap. Sort uses fewer than 2 N lg N comparisons to sort N elements. Prf: Build heap bottom up in linear time. Then swap largest item with last item, decrement heap size, and sift. Down the new root in log time. A bound of 3 N lg N is thus easy to get, but a more careful counting shows that it is really 2 N lg N.

Heap. Select Property 9. 6: Heap-based selection finds the kth largest element in time proportional to N when k is small or close to N, and in time N lg N otherwise. Build a heap (linear time), then remove k largest items (2 k lg N operations), or a minimum-oriented heap and remove N-k smallest items.

Which Sort to Use? Heapsort? Quicksort? Mergesort? Often an issue of choosing between stability and using extra space. Heapsort vs. quicksort reduces to choice between average-case speed and worstcase speed. Mergesort and quicksort exhibit good locality (plays nice with virtual memory).

Next Binomial queues (fast join for PQ) Radix Sort