Quicksort quick Sort A low high ifhigh low

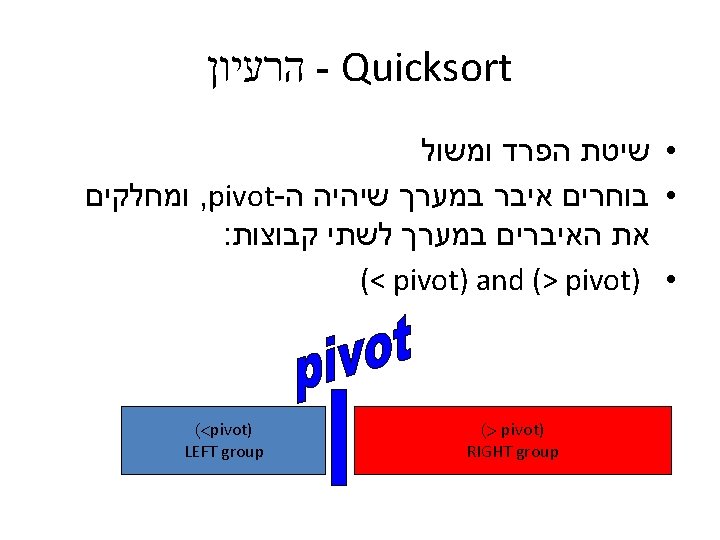
Quicksort

האלגוריתם quick. Sort( A, low, high ) if(high > low) pivot ← partition(A, low, high) quick. Sort(A, low, pivot-1 ) quick. Sort(A, pivot+1, high) quick. Sort(A, 0, length(A)-1) int partition( A, low, high ) pivot_value ← A[low] left ← low pivot ← left right ← high while ( left < right ) // Move left while item < pivot while( left < high && A[left] ≤ pivot_value) left++ // Move right while item > pivot while( A[right] > pivot_value) right— // Make sure right has not passed left if( left < right ) SWAP(A, left, right) // right is final position for the pivot A[low] ← A[right] ← pivot_item return right

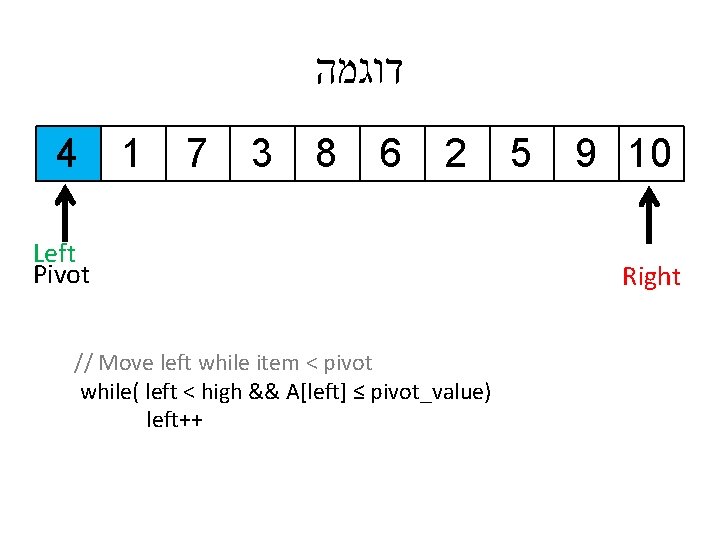
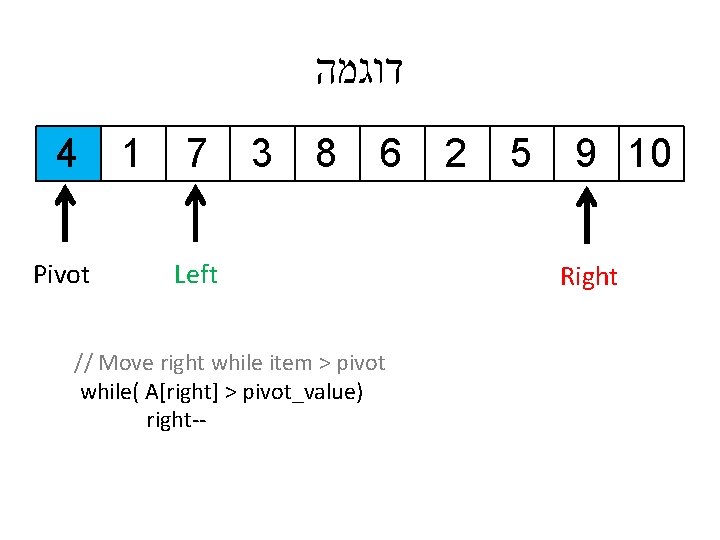
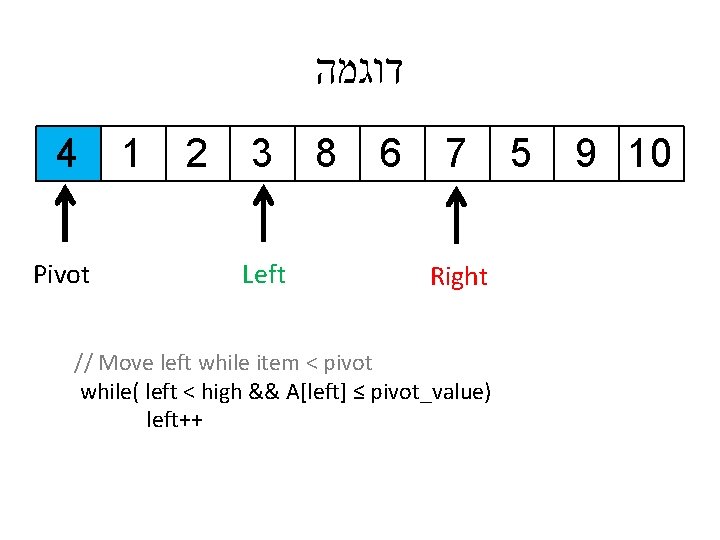
דוגמה 4 1 7 3 8 6 2 Left Pivot // Move left while item < pivot while( left < high && A[left] ≤ pivot_value) left++ 5 9 10 Right

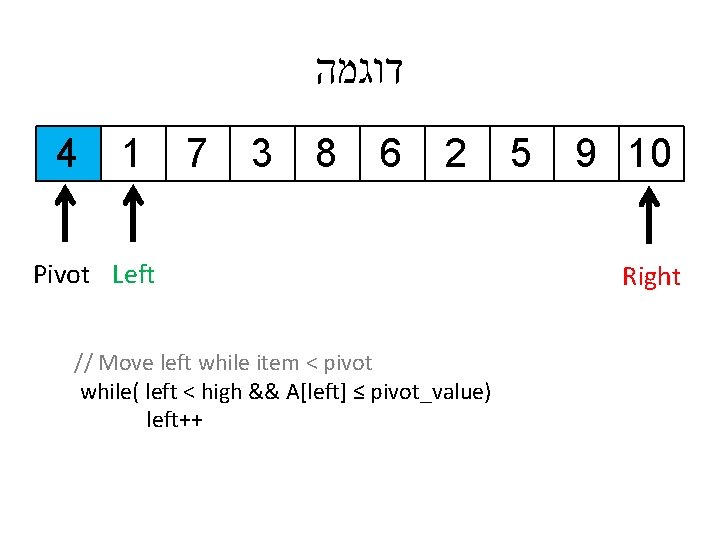
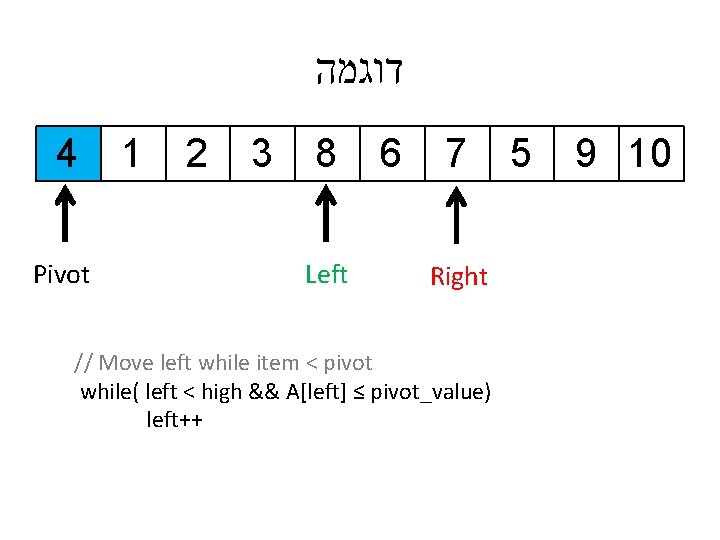
דוגמה 4 1 7 3 8 6 2 Pivot Left // Move left while item < pivot while( left < high && A[left] ≤ pivot_value) left++ 5 9 10 Right

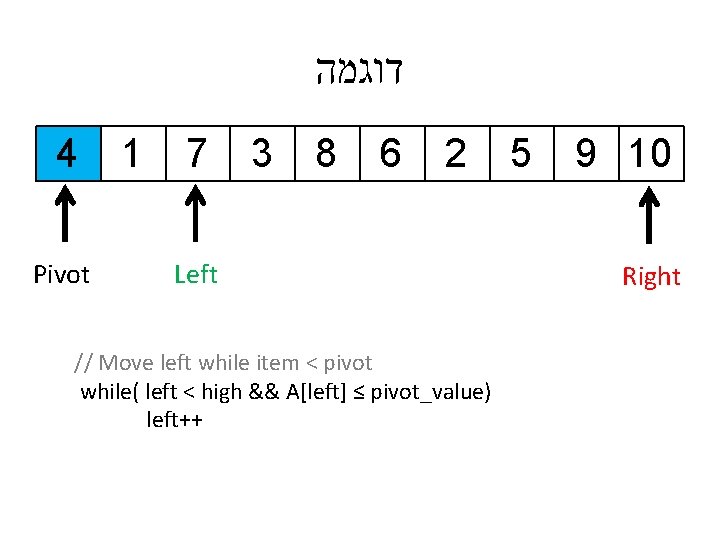
דוגמה 4 Pivot 1 7 3 8 6 2 Left // Move left while item < pivot while( left < high && A[left] ≤ pivot_value) left++ 5 9 10 Right

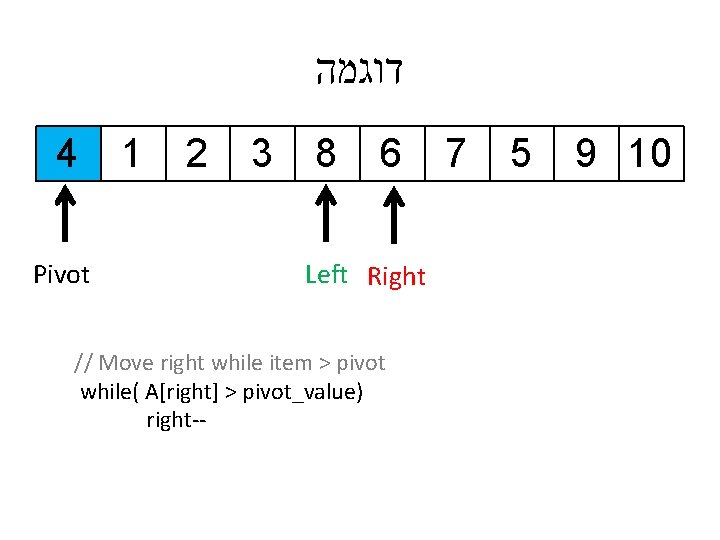
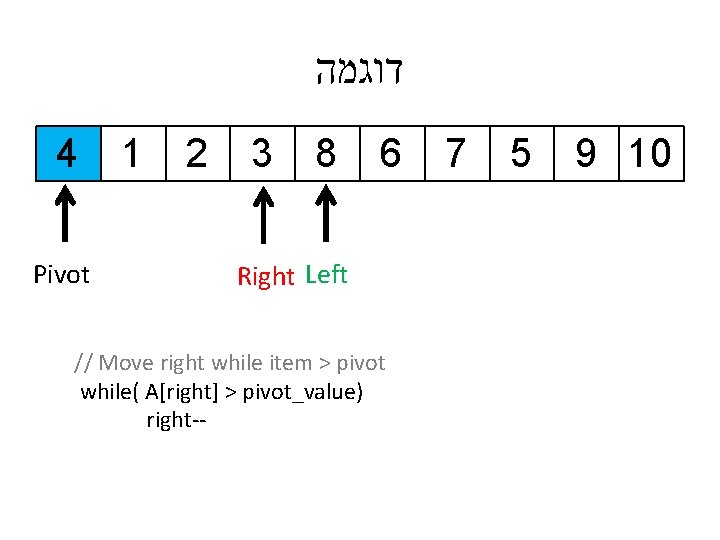
דוגמה 4 Pivot 1 7 3 8 6 Left // Move right while item > pivot while( A[right] > pivot_value) right-- 2 5 9 10 Right

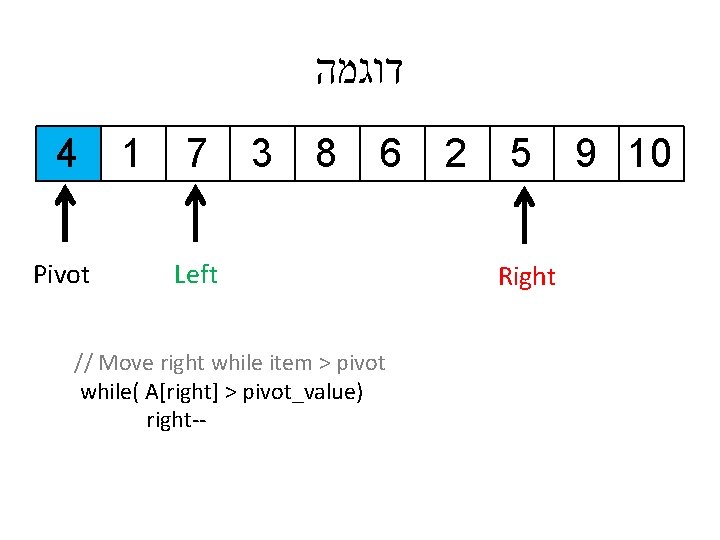
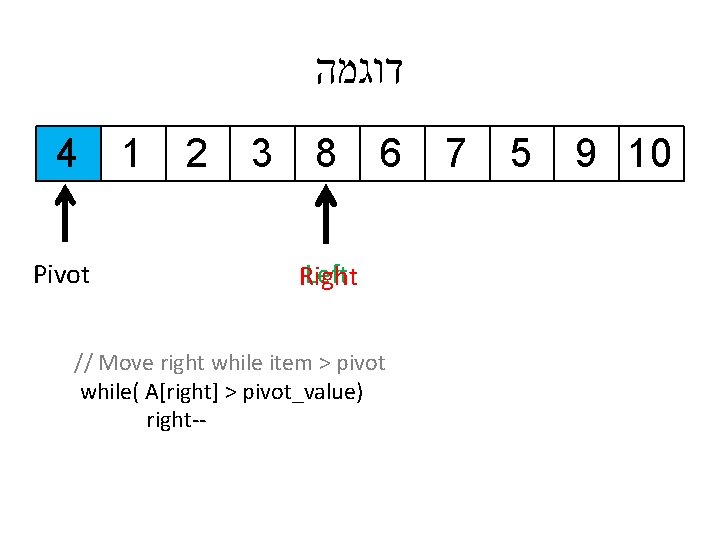
דוגמה 4 Pivot 1 7 3 8 6 Left // Move right while item > pivot while( A[right] > pivot_value) right-- 2 5 Right 9 10

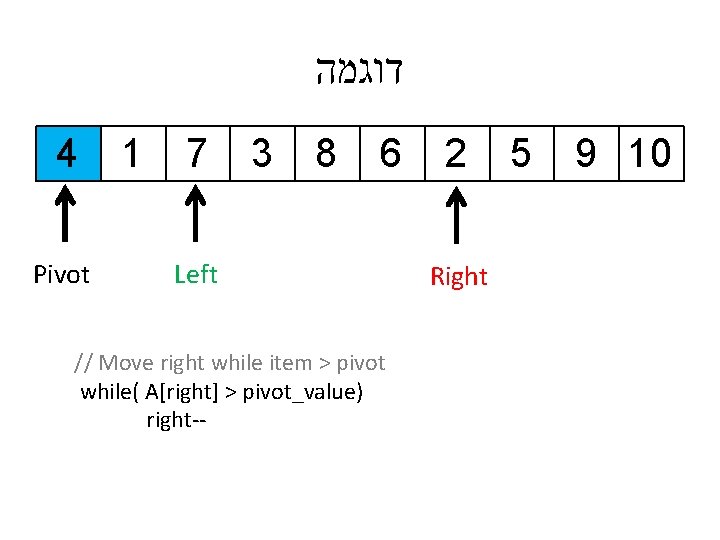
דוגמה 4 Pivot 1 7 3 8 6 Left // Move right while item > pivot while( A[right] > pivot_value) right-- 2 Right 5 9 10

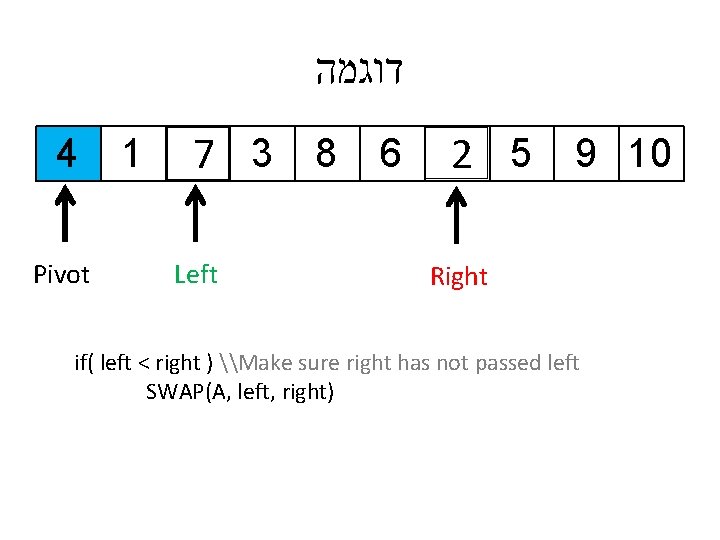
דוגמה 4 Pivot 1 7 3 8 6 Left 2 5 9 10 Right if( left < right ) \Make sure right has not passed left SWAP(A, left, right)

דוגמה 4 Pivot 1 2 3 Left 8 6 7 Right // Move left while item < pivot while( left < high && A[left] ≤ pivot_value) left++ 5 9 10

דוגמה 4 Pivot 1 2 3 8 Left 6 7 Right // Move left while item < pivot while( left < high && A[left] ≤ pivot_value) left++ 5 9 10

דוגמה 4 Pivot 1 2 3 8 6 Left Right // Move right while item > pivot while( A[right] > pivot_value) right-- 7 5 9 10

דוגמה 4 Pivot 1 2 3 8 6 Left Right // Move right while item > pivot while( A[right] > pivot_value) right-- 7 5 9 10

דוגמה 4 Pivot 1 2 3 8 6 Right Left // Move right while item > pivot while( A[right] > pivot_value) right-- 7 5 9 10

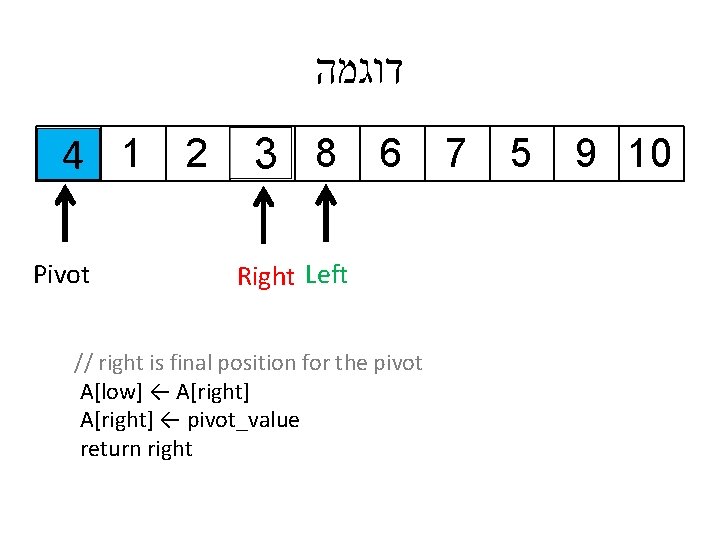
דוגמה 4 1 2 Pivot 3 8 6 7 5 9 10 Right Left // right is final position for the pivot A[low] ← A[right] ← pivot_value return right

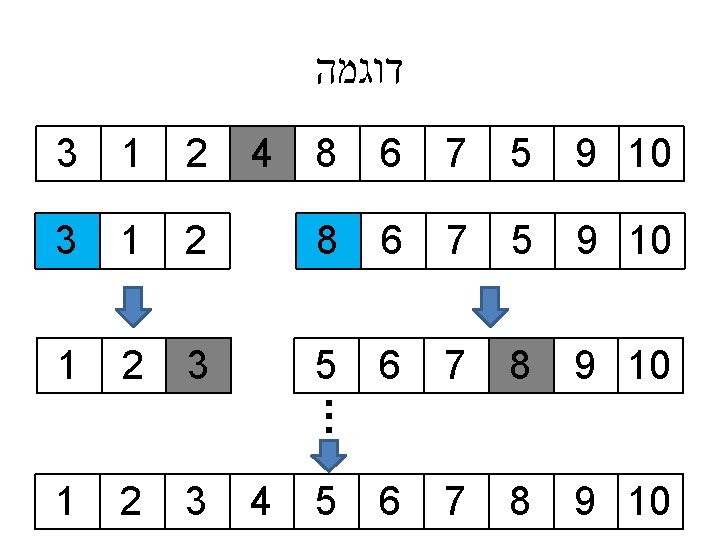
דוגמה 4 9 10 5 7 6 8 2 9 10 8 7 6 5 . . . 3 2 9 10 8 7 6 5 3 2 4 2 1 3 1 1

Quicksort • stable sorting algorithms: maintain the relative order of records with equal keys • Is the Quick. Sort version above stable? • No

פתרון - 3 שאלה Select(k, S) // returns k-th element in S. pick x in S partition S into: // Slightly different variant of partition() max(L) < x, E = {x}, x < min(G) if k ≤ length(L) // Searching for item ≤ x. return Select(k, L) else if k ≤ length(L) + length(E) // Found return x else // Searching for item ≥ x. return Select(k - length(L) - length(E), G) pivot , בגודלו k- ה האיבר – x : קבוצות 3 - ל S את מחלקים שלב בכל x- מ הגדולים האיברים כל -G x- מ הקטנים האיברים כל -L x- ל השווים האיברים כל -E G- ב או L- ב רקורסיבית אותו לחפש ממשיכים , x את מצאנו לא אם

Counting Sort A sort algorithm that is not based on comparisons, and supports duplicate keys. • A is an input array of length n. • B is the output array of length n too. • C is an auxiliary array of size k. • Assumption: the input array A consists of elements with integer keys in the range [1. . k].

Counting Sort for i ← 1 to k C[i] ← = 0 for j ← 1 to n C[A[j]] ← C[A[j]] + 1 // C[i] = the number of appearances of i in A. for i ← 2 to k C[i] ← C[i] + C[i-1] // C[i] = the number of elements in A that are ≤ i for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] - 1 return B

Quick Sort for i ← 1 to k C[i] ← = 0 A 3 2 3 C 0 0 0 1 3 1

Quick Sort for j ← 1 to n C[A[j]] ← C[A[j]] + 1 // C[i] = the number of appearances of i in A 3 2 3 C 2 1 3 1

Quick Sort for i ← 2 to k C[i] ← C[i] + C[i-1] // C[i] = the number of elements in A that are ≤ i A 3 2 3 C 2 3 6 1 3 1

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 A 3 2 3 C 2 3 6 B 1 3 1

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=6, A[6]=1, C[1]=2 A 3 2 3 C 2 3 6 B 1 3 1

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=6, A[6]=1, C[1]=2 A 3 2 3 C 1 3 6 B 1 1 3 1

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=5, A[5]=3, C[3]=6 A 3 2 3 C 1 3 6 B 1 1 3 1

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=5, A[5]=3, C[3]=6 A 3 2 3 C 1 3 5 B 1 1 3

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=4, A[4]=1, C[1]=1 A 3 2 3 C 1 3 5 B 1 1 3

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=4, A[4]=1, C[1]=1 A 3 2 3 C 0 3 5 B 1 1 1 3

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=3, A[3]=3, C[3]=5 A 3 2 3 C 0 3 5 B 1 1 1 3

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=3, A[3]=3, C[3]=5 A 3 2 3 C 0 3 4 B 1 1 1 3 3

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=2, A[2]=2, C[2]=3 A 3 2 3 C 0 3 4 B 1 1 1 3 3

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=2, A[2]=2, C[2]=3 A 3 2 3 C 0 2 4 B 1 1 2 1 3 3

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=1, A[1]=3, C[3]=4 A 3 2 3 C 0 2 4 B 1 1 2 1 3 3

Quick Sort for j ← n downto 1 B[C[A[j]]] ← A[j] C[A[j]] ← C[A[j]] – 1 j=1, A[1]=3, C[3]=4 A 3 2 3 C 0 2 3 B 1 1 2 1 3 3 3

Bucket Sort •

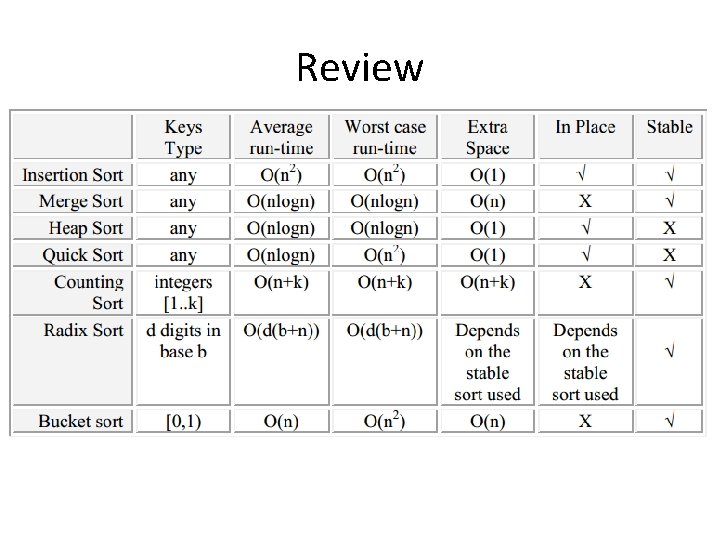
Review