Covering the Sphere A PiDay Activity NOYCE June

Covering the Sphere: A Pi-Day Activity NOYCE, June 2007 Presented by : Kimberly Halsey Matthew Wells Department of Mathematics Bath County High School (KY) University of Kentucky

Background of Presenters l Kimberly Halsey: ¡ ¡ ¡ High School teacher at Bath County HS Teaches classes ranging from basic Algebra to Pre-Calc Has been a teacher for 15 years l Matthew Wells ¡ ¡ ¡ Mathematics Graduate doctoral student Teaches two classes per semester at University of Kentucky Going into 5 th year in Graduate School

Philosophy to the Mathematics l To get students to understand the mathematics in a conceptual way l Build a foundation that will be beneficial for later mathematics l Challenge students to think abstractly and problem solve

Mathematics Focus l Geometry and Algebra l Area of a circle l Surface Area of a sphere l Specific focus on PI (good for a Pi-Day activity) l The main activity involved the formula for Surface area of a sphere

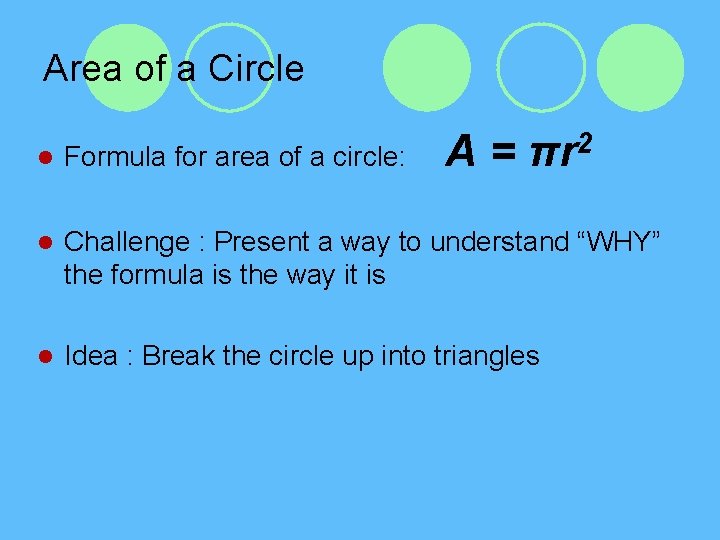
Area of a Circle A = πr 2 l Formula for area of a circle: l Challenge : Present a way to understand “WHY” the formula is the way it is l Idea : Break the circle up into triangles

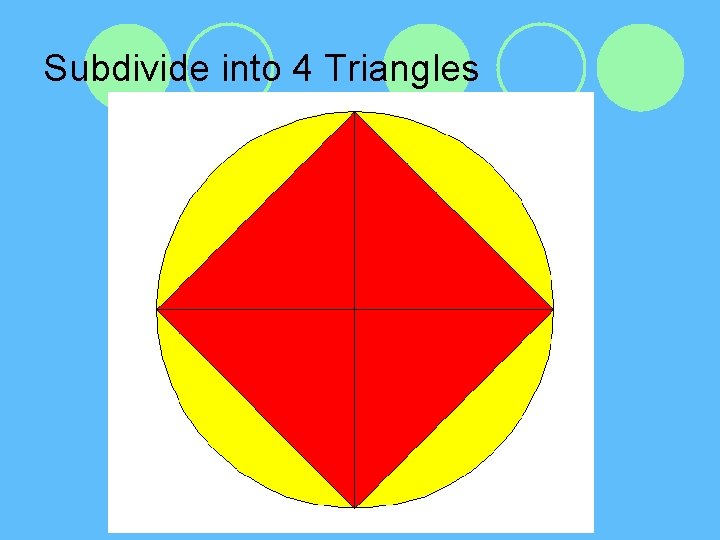
Subdivide into 4 Triangles

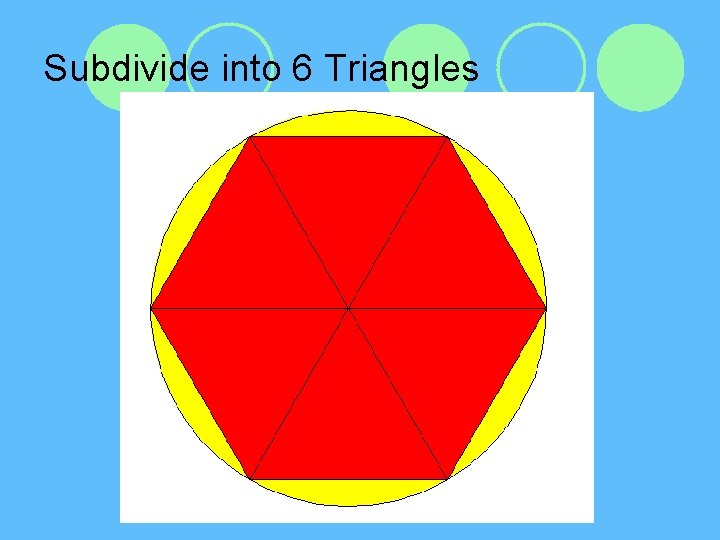
Subdivide into 6 Triangles

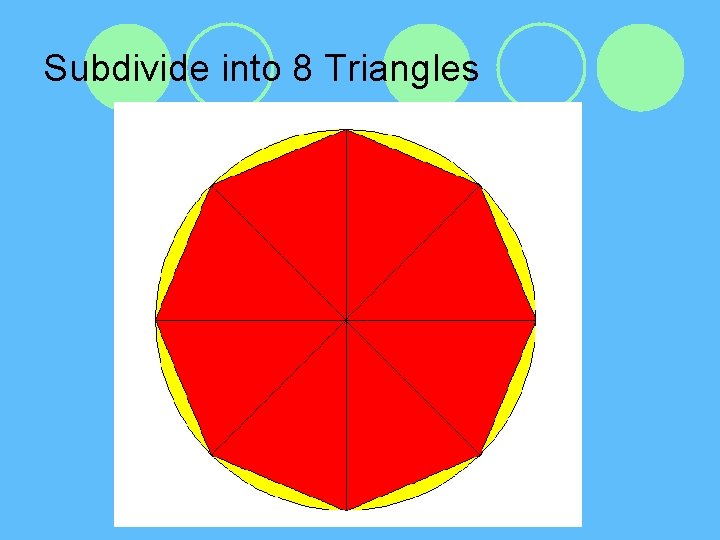
Subdivide into 8 Triangles

Subdivide into 12 Triangles

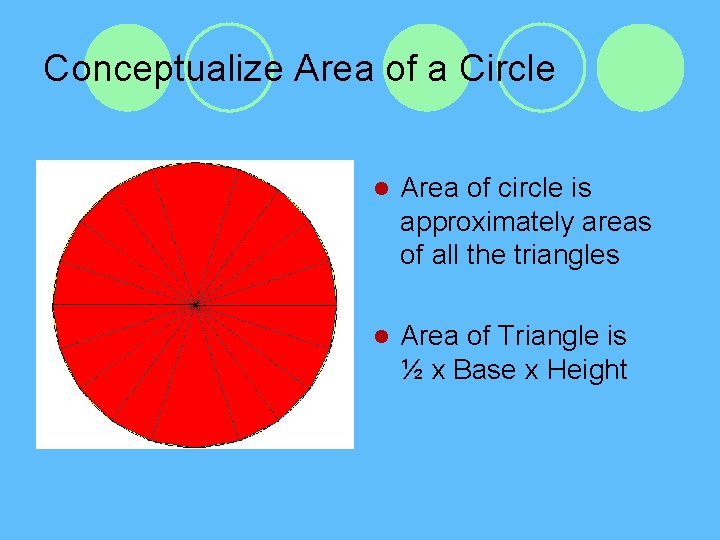
Conceptualize Area of a Circle l Area of circle is approximately areas of all the triangles l Area of Triangle is ½ x Base x Height

Ideas Observed l Students understand areas of triangles and squares easier than areas of round objects l There is a connection between triangles and circles l The students can measure one triangle easily and find the areas of all the triangles

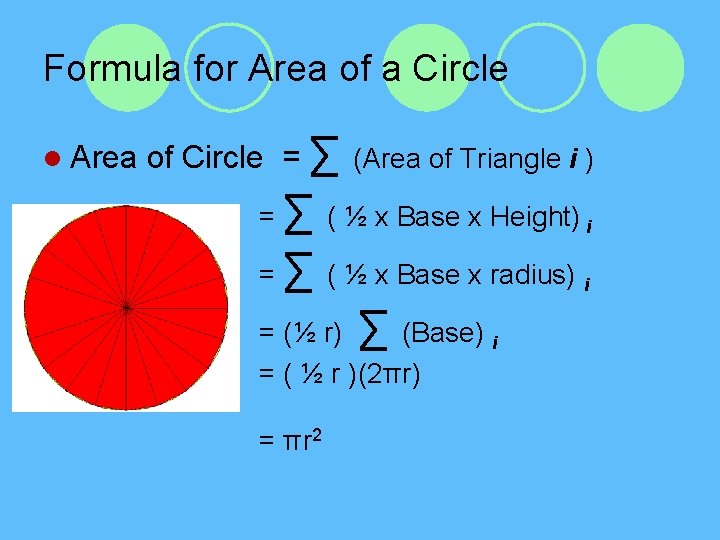
Formula for Area of a Circle l Area of Circle = ∑ (Area of Triangle i ) = ∑ ( ½ x Base x Height) i = ∑ ( ½ x Base x radius) i = (½ r) ∑ (Base) i = ( ½ r )(2πr) = πr 2

Ideas Observed (part II) l Students understand areas of triangles and squares easier than areas of round objects l There is a connection between triangles and circles l The Circumference of a circle is used (how might this apply to Spheres? ? ? )

Surface Area l Question: How do we find the surface area of a sphere? l Question: Can we get the students to understand the concept of Surface Area?

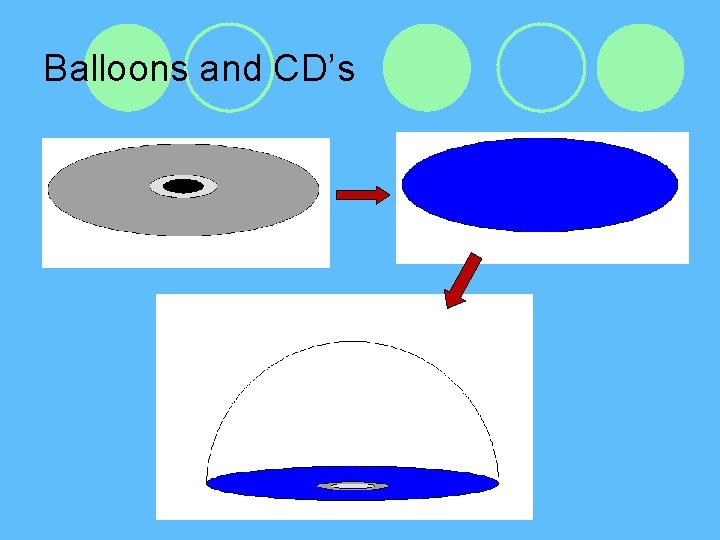
Balloons and CD’s

Observations l Students can connect the idea of Surface Area to 2 -dimensional area l Idea of using triangles is easily transferable to higher dimension l Question: Are the triangles really triangles? l ANSWER: NO!!!

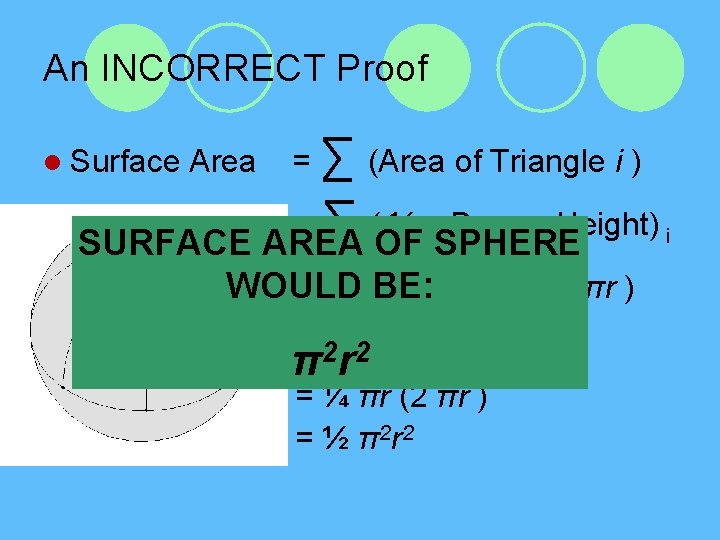
An INCORRECT Proof l Surface l l l Area = ∑ (Area of Triangle i ) = ∑ ( ½ x Base x Height) i SURFACE AREA OF SPHERE WOULD = ∑ (BE: ½ x Base x ½πr ) = 2¼r 2πr ∑ π (Base)I = ¼ πr (2 πr ) = ½ π 2 r 2

Comments about the Proof l The “triangles” are not actually triangles l When the “triangles” are made thinner, the error in the formula remains l Can we assimilate what we did for the area of a circle? l SOLUTION: Use triangles that shrink from all sides

Pi-Day Activity l Materials: One foam Hemisphere Pair of scissors Box of pins Paper triangles

Pi-Day Activity l Cut out the triangles and attach them to the round part of the hemisphere with three pins:

Pi-Day Activity l Try to cover the Hemisphere with as many NON-OVERLAPPING triangles as possible: CORRECT INCORRECT

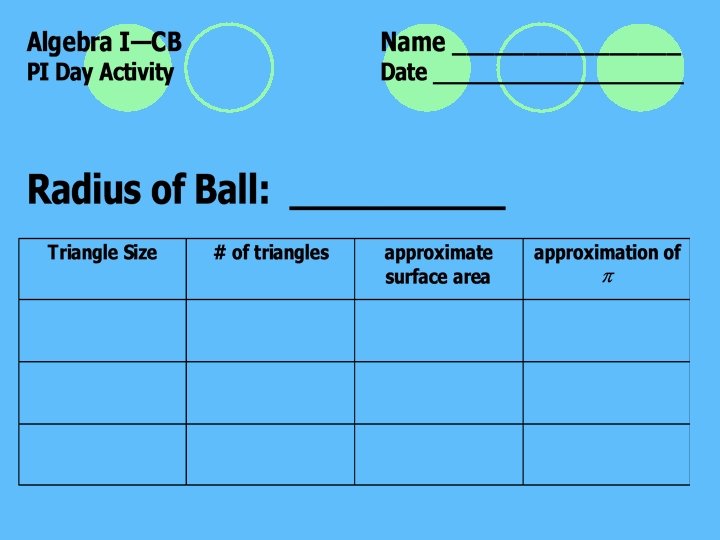
Pi-Day Activity Count up the number of triangles 2) Measure the radius of the ball 3) Measure the length of a side of the triangle 4) Collect and Compare 1)

Students doing this Activity

More Students

Even More Students

HINT: Volume of a Pyramid is : Further Activities (1/3) x Base x Height l Can you find the volume of a sphere using the ideas presented today?

Contact Information q Matthew Wells mwells@ms. uky. edu (859) 257 -7216 q Kimberly Halsey Kimberly. Halsey@Bath. kyschools. us