COSC 2006 Data Structures I Recursion III kth






















- Slides: 25

COSC 2006 Data Structures I Recursion III

kth smallest n Can be solved by sorting, but this does more work than needed (why? ) n n solving kth smallest for all k More efficient solution possible: n n n Pick an element, any element partition the other elements into two sets: those smaller (S 1) and those bigger (S 2) If S 1 has k-1 members, we got lucky! If S 1 has at least k members, recurse to find the kth smallest in S 1 Otherwise recurse to find the kth smallest in S 2 …

kth smallest: Devil in the details What about this last case? n We dispensed with |S 1| + 1 elements! n So we are looking for the ___th smallest element in S 2 n (k - (|S 1| + 1))th n Need to “pass” subarray with first, last n So, |S 1| = pivot. Index - first

kth smallest: partial code This motivates the details: k. Small(k, an. Array, first, last) choose a pivot. Index if (k < pivot. Index - first + 1) return k. Small(k, an. Array, first, pivot. Index-1) else if (k == pivot. Index - first + 1) return p else return k. Small(k - (pivot. Index-first+1), an. Array, pivot. Index+1, last)

Problems with Recursion Memory (stack) exhaustion: if many stack frames are pushed - can run out of space for stack Time: each recursive call requires time to set up a new stack frame, copy in actual parameter values and transfer execution

Problems with Recursion Any recursive algorithm can be rewritten using iterative technique - it will be longer and more likely to have problems but will run faster.

Recursion Vs Iteration n n Note that just because we can use recursion to solve a problem, that does not mean this is the optimal solution. For instance, we usually would not use recursion to solve the sum of 1 to N problem, because the iterative version is easier to understand requires less memory is N is a large number.

Recursion Vs Iteration n The iterative solution is easier to understand: sum = 0; for(int number = 1; number <=N; number++) sum += number; n Recursion has memory overhead. However, for some problems, recursion provides an elegant solution, often cleaner than an iterative version

Example: Towers of Hanoi n n For some problems, recursive solution is the A B only reasonable solution Given: · N disks & three poles: n n n · · n C A the source B the destination C the spare (temporary) The disks are of different sizes & have holes in the middle Only one disk can be removed at a time A larger disk can't be placed on a smaller one Initially all disks are on pole A Required: · Move the disks, one-by-one, from pole(peg) A to B, using pole C as spare

Example: Towers of Hanoi n Solution: n Only one disk (N=1, First base case): n n Move the disk from the source peg A to the destination peg B Only two disks (N=2, Second base case): Move the top disk from peg A to peg C n Move the second disk from peg A to peg B n Move the top disk from peg C to peg B n

Example: Towers of Hanoi n Solution: n Three disks (N=3): Move top disk from peg A to peg B n Move second disk from peg A to peg C n Move top disk from peg B to peg C n Move the remaining bottom disk from peg A to peg B n Move the top disk from peg C to peg A n Move second disk from peg C to peg B n Move top disk from peg A to peg B C B A n

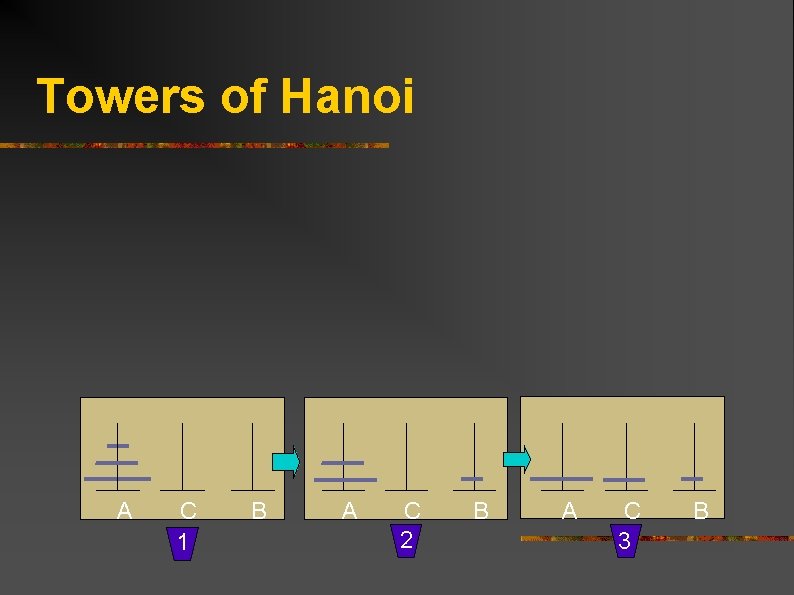
Towers of Hanoi A C 1 B A C 2 B A C 3 B

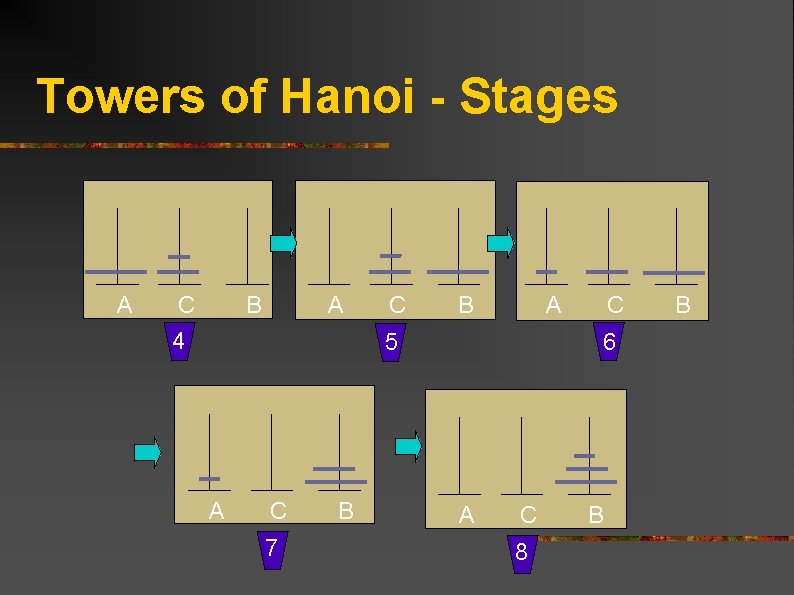
Towers of Hanoi - Stages A C 4 B A C B 6 5 A C 7 B C A A C 8 B B

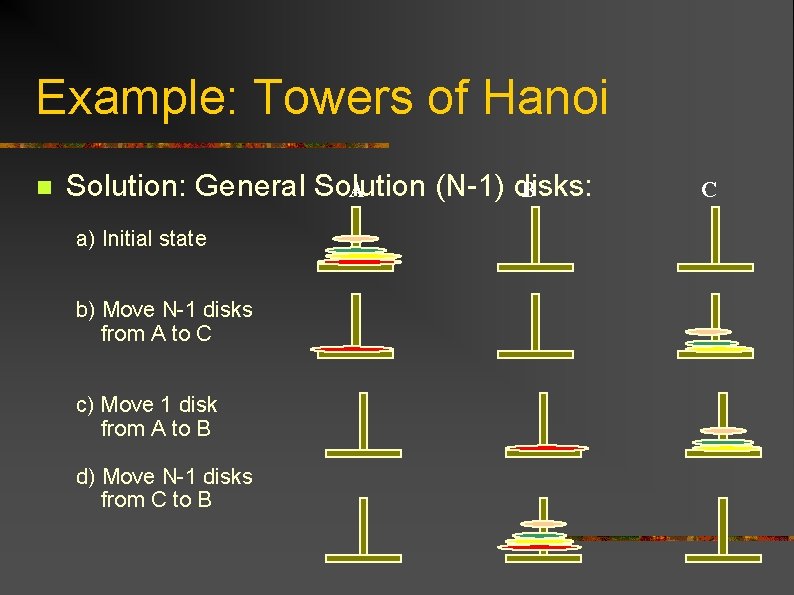
Example: Towers of Hanoi n Solution: n General Solution (N-1) disks: Move the top (N-1) disks to Temp pole n Move the bottom disk to the destination n Move the N-1 disks from Temp to the destination n

Example: Towers of Hanoi n Solution: General Solution (N-1) disks: A B a) Initial state b) Move N-1 disks from A to C c) Move 1 disk from A to B d) Move N-1 disks from C to B C

Towers of Hanoi First let’s play with blocks … solve. Towers(count, source, dest, spare) if (count is 1) { move a disk directly from source to dest else solve. Towers(count-1, source, spare, dest) solve. Towers(1, source, dest, spare) solve. Towers(count-1, spare, dest, source)

Towers of Hanoi - Algorithm public static void solve. Towers(int n, char source, char dest, char intermed) { if (n == 1) System. out. println("move a disk from " + source + " to " + dest); else { 2 solve. Towers(n-1, source, intermed, dest); solve. Towers(1, source, dest, intermed); solve. Towers(n-1, intermed, dest, source); } 3 } original call: solve. Towers ( 3, 'A', 'C', 'B'); 1

Example: Towers of Hanoi n Observations n Solution analog to mathematical induction n If we can solve the problem for N-1 disks, then we can solve it for N disks In each move, the source, destination, and temporary poles change locations Three recursive calls inside the function

Review n When you solve a problem by solving two or more smaller problems, each of the smaller problems must be ______ the base case than the original problem. closer to n farther to n either closer to or the same “distance” from n n either from 19 farther to or the same “distance”

Review n In a sorted array, the kth smallest item is given by ______. an. Array[k-1] n an. Array[k] n an. Array[SIZE-k] n an. Array[SIZE+k] n 20

Review n A recursive solution that finds the factorial of n always reduces the problem size by ______ at each recursive call. 1 n 2 n half n one-third n 21

Review n In the recursive solution to the kth smallest item problem, the problem size decreases by ______ at each recursive call. 1 n at least 1 n half n at least half n 22

Review n In the recursive solution to the Towers of Hanoi problem, the number of disks to move ______ at each recursive call. decreases by 1 n increases by 1 n decreases by half n increases by half n 23

Review n A recursive solution that finds the factorial of n generates ______ recursive calls. n-1 n n+1 n n*2 n 24

Review n In the Fibonacci sequence, which of the following integers comes after the sequence 1, 1, 2, 3? 3 n 4 n 5 n 6 n 25