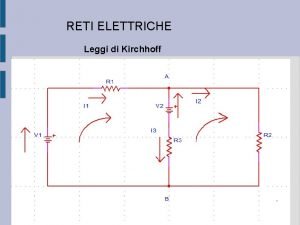
Corso di Elettrotecnica Allievi aerospaziali Reti Elettriche Parte





















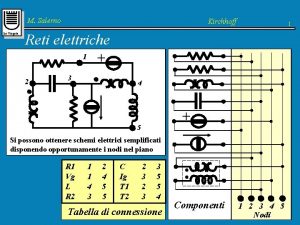
- Slides: 36

Corso di Elettrotecnica Allievi aerospaziali Reti Elettriche – Parte II Revisione aggiornata al 7 4 2011 (www. elettrotecnica. unina. it)

Circuiti in regime lentamente variabile Analisi dei circuiti in regime sinusoidale

Bipoli elementari lineari

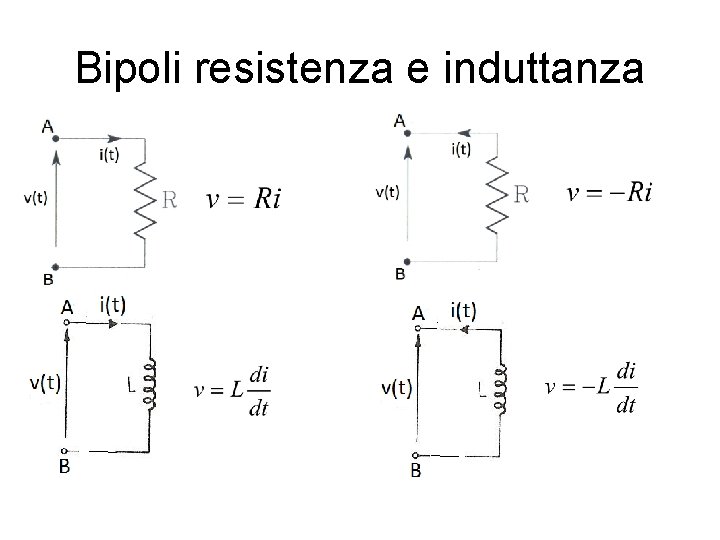
Bipoli resistenza e induttanza

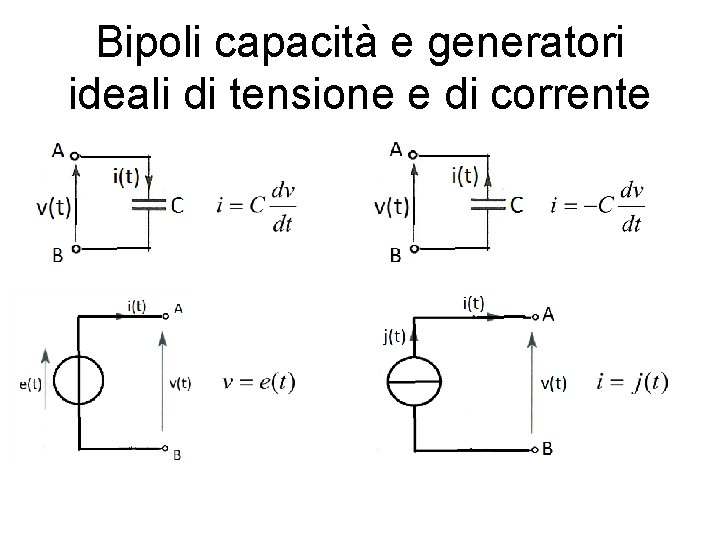
Bipoli capacità e generatori ideali di tensione e di corrente

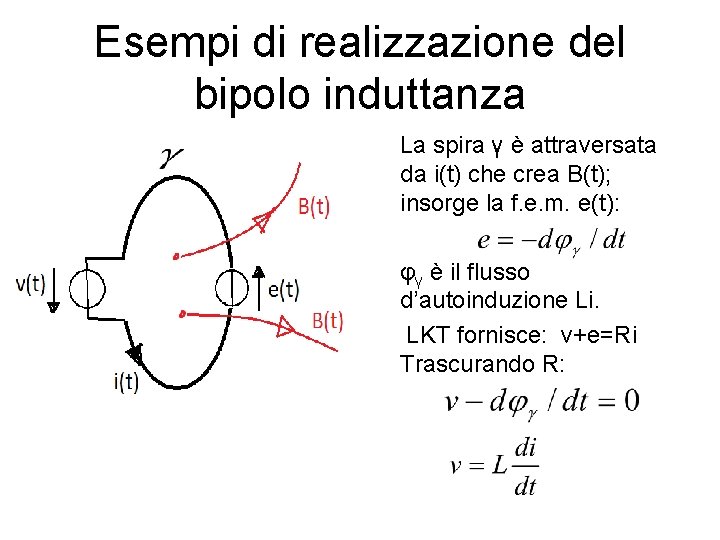
Esempi di realizzazione del bipolo induttanza La spira γ è attraversata da i(t) che crea B(t); insorge la f. e. m. e(t): φγ è il flusso d’autoinduzione Li. LKT fornisce: v+e=Ri Trascurando R:

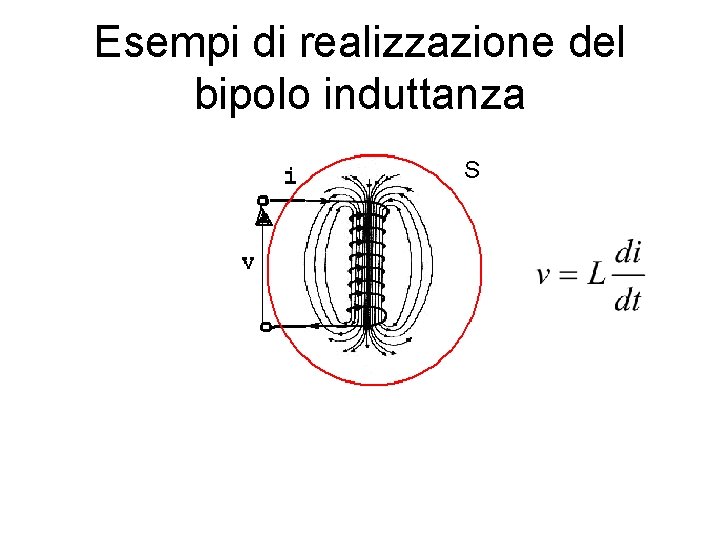
Esempi di realizzazione del bipolo induttanza S

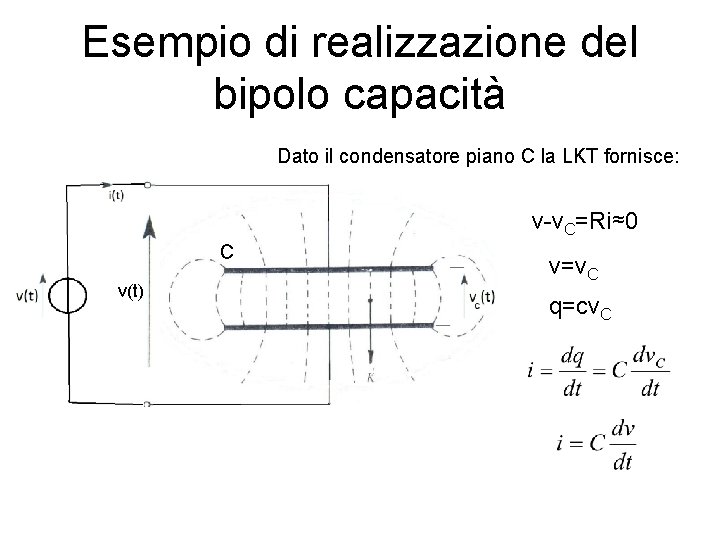
Esempio di realizzazione del bipolo capacità Dato il condensatore piano C la LKT fornisce: v-v. C=Ri≈0 C v(t) v=v. C q=cv. C

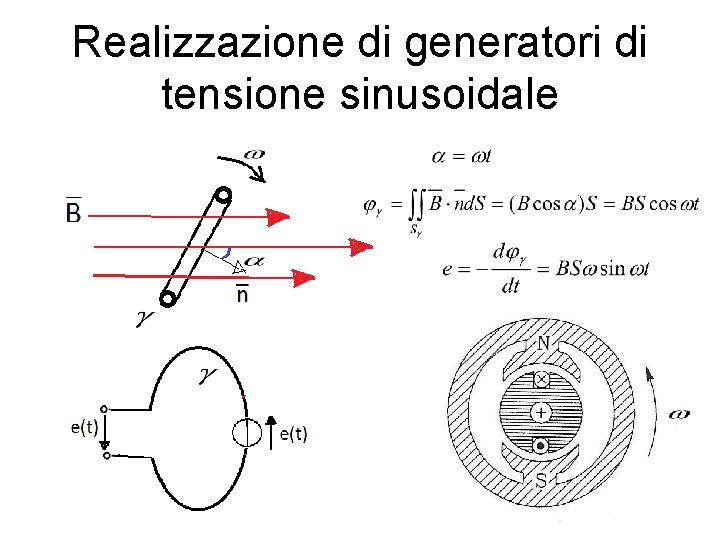
Realizzazione di generatori di tensione sinusoidale

Richiami sulle funzioni periodiche Si dice periodica una funzione del tempo y=f(t) che assume valori che si ripetono a "intervalli" regolari T. Si ha: Si dice periodo il valore minimo di T (se esiste) che soddisfa tale relazione.

Richiami sulle funzioni periodiche La frequenza è il numero di cicli in un secondo: f=1/T [Hertz] La pulsazione è la quantità: ω=2πf=2π/T [Rad/sec] Si dice valore medio di f(t) nel periodo T la quantità: indipendente da t 0. Se Fm=0, f(t) si dice alternata o alternativa. Si dice valore efficace di f: (valore quadratico medio)

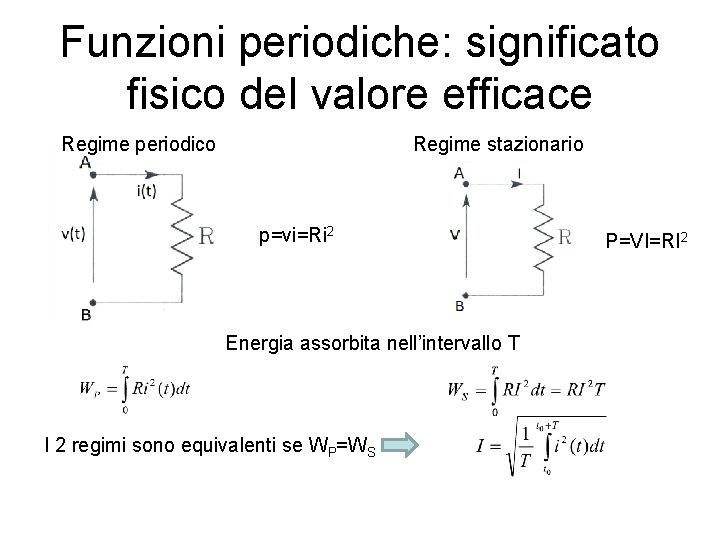
Funzioni periodiche: significato fisico del valore efficace Regime periodico Regime stazionario p=vi=Ri 2 Energia assorbita nell’intervallo T I 2 regimi sono equivalenti se WP=WS P=VI=RI 2

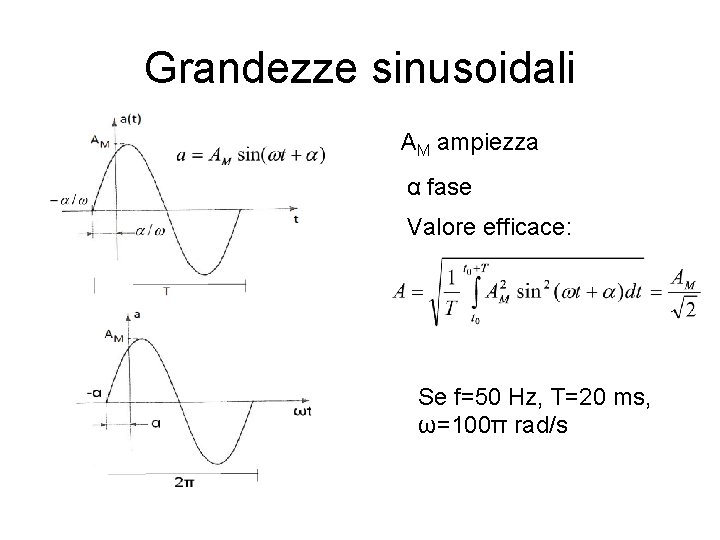
Grandezze sinusoidali AM ampiezza α fase Valore efficace: Se f=50 Hz, T=20 ms, ω=100π rad/s

Richiami sui numeri complessi Rappresentazione geometrica nel piano complesso z è l’affissa complessa di P Rappresentazione algebrica z=x+jy dove j è l’unità immaginaria definita da j 2=-1. x è la parte reale di z y la parte immaginaria z è indicato anche come (x , y). P è l’immagine di z. Gli assi x (asse reale) e y (asse immaginario) contengono le immagini di tutti i numeri reali e puramente immaginari.

Richiami sui numeri complessi Rappresentazione vettoriale di z sul piano complesso Complesso coniugato di z=x+jy: z*=x-jy Modulo di z: Argomento di z (anomalia del vettore OP) ρ e θ sono le coordinate polari di z che si può indicare anche come z=[ρ, θ]

Richiami sui numeri complessi Rappresentazione trigonometrica di z=x+jy: z=ρ(cosθ+jsin θ) Per la formula di Eulero ejθ=cosθ+jsinθ si ha la formulazione esponenziale complessa di z: z=[ρ, θ]= ρ ejθ

Operazioni sui numeri complessi SOMMA

Prodotto di numeri complessi Rappresentazione algebrica Rappresentazione polare

Divisione di numeri complessi Rappresentazione algebrica Rappresentazione polare

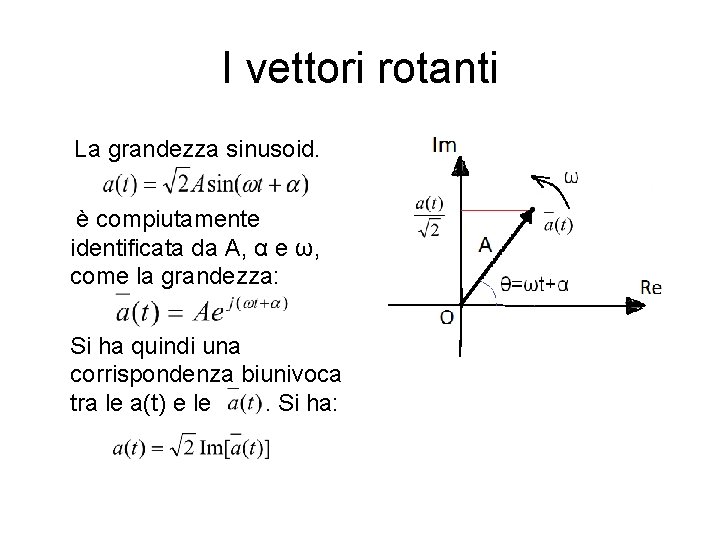
I vettori rotanti La grandezza sinusoid. è compiutamente identificata da A, α e ω, come la grandezza: Si ha quindi una corrispondenza biunivoca tra le a(t) e le. Si ha:

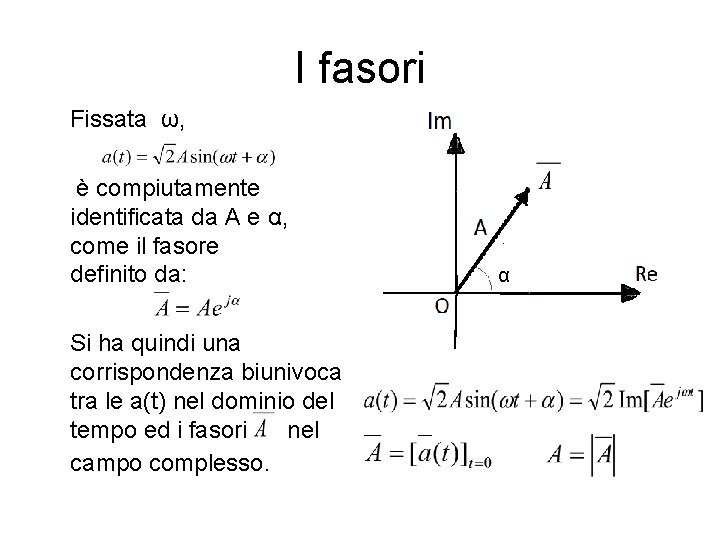
I fasori Fissata ω, è compiutamente identificata da A e α, come il fasore definito da: Si ha quindi una corrispondenza biunivoca tra le a(t) nel dominio del tempo ed i fasori nel campo complesso. α

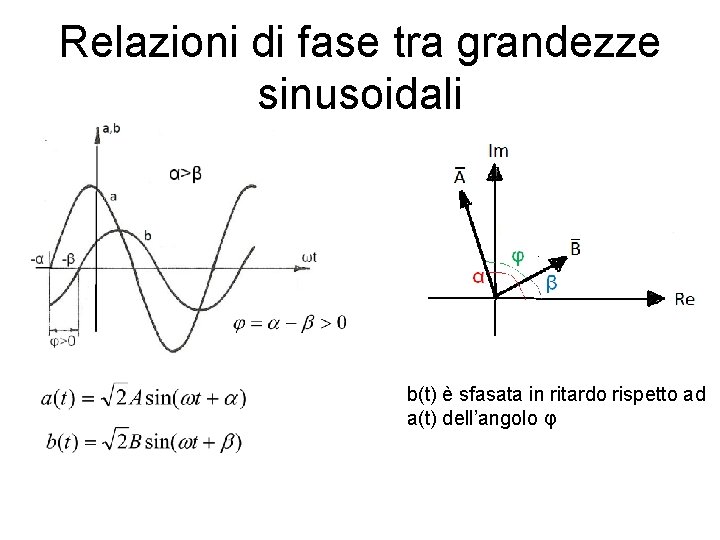
Relazioni di fase tra grandezze sinusoidali b(t) è sfasata in ritardo rispetto ad a(t) dell’angolo φ

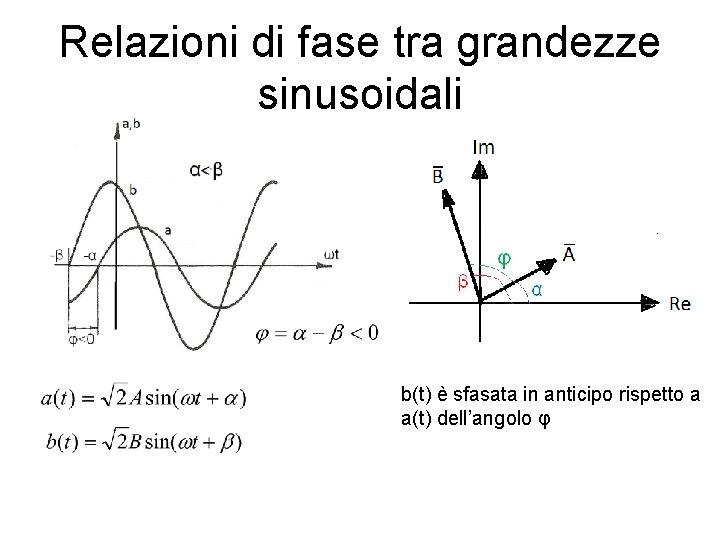
Relazioni di fase tra grandezze sinusoidali b(t) è sfasata in anticipo rispetto a a(t) dell’angolo φ

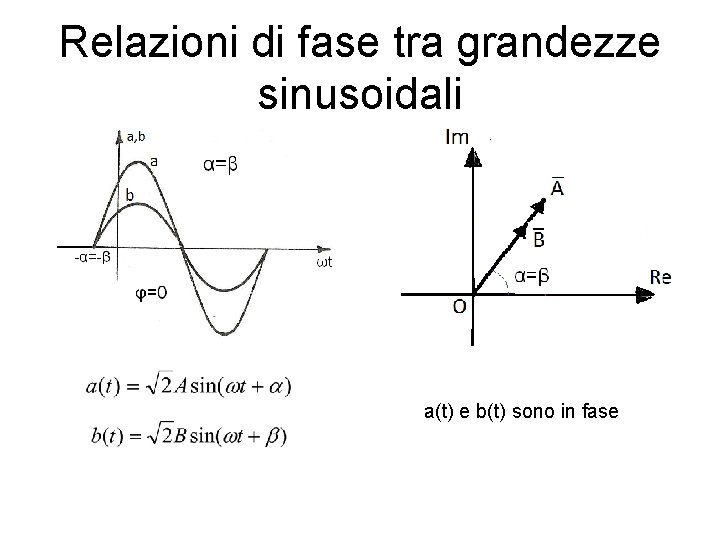
Relazioni di fase tra grandezze sinusoidali a(t) e b(t) sono in fase

Le operazioni sulle grandezze sinusoidali Date dove: O

Prodotto di una grandezza sinusoidale per una costante Date: ed una costante reale k>0, α

Derivata temporale di una grandezza sinusoidale Data α

Prodotto di un fasore per un numero complesso

Prodotto di grandezze sinusoidali

Bipolo resistenza in regime sinusoidale Dominio dei fasori Dominio del tempo impedenza

Bipolo induttanza in regime sinusoidale Dominio dei fasori Dominio del tempo impedenza Reattanza

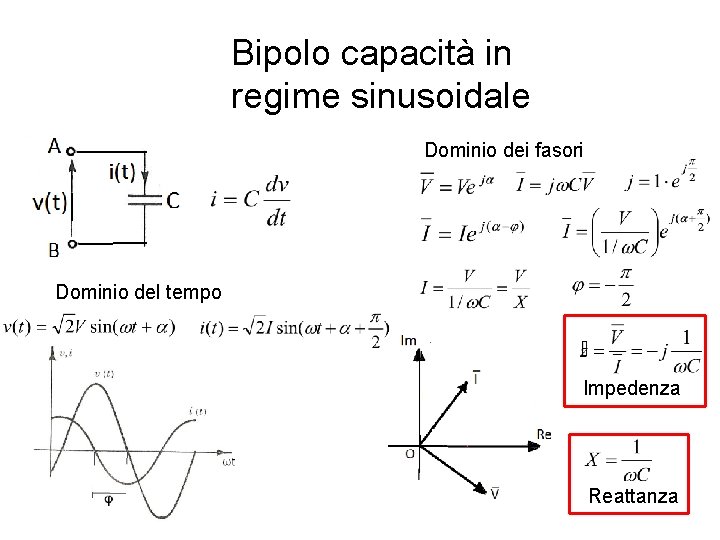
Bipolo capacità in regime sinusoidale Dominio dei fasori Dominio del tempo Impedenza Reattanza

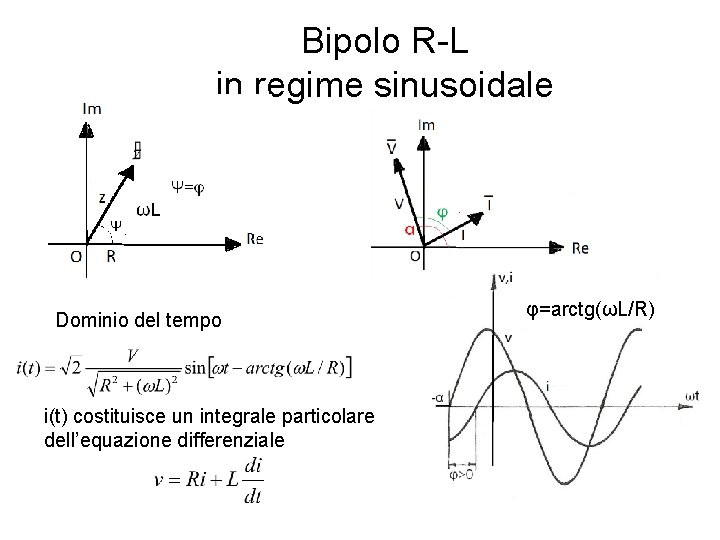
Bipolo R-L in regime sinusoidale Dominio del tempo LKT Dominio dei fasori

Bipolo R-L in regime sinusoidale Dominio del tempo i(t) costituisce un integrale particolare dell’equazione differenziale φ=arctg(ωL/R)

Bipolo R-L in regime transitorio L’integrale generale dell’equazione differenziale: è dove ip(t) è un integrale particolare e λ è la radice dell’equaz. caratteristica dell’equaz. omogenea associata R+λL=0 (T=L/R costante di tempo) (trascurabile per t>5 T)

Bipolo R-L in regime transitorio Se ad es. R=10 Ω, X=ωL=10 Ω, per f=50 Hz ω=100π rad/s, L=0, 1/π Henry, T=L/R=0, 01/π=3, 18 ms e dopo circa 16 ms il termine transitorio ke-t/T è trascurabile. Per il calcolo di k occorre imporre la condizione iniziale per t=0+. Se I 0=[i(t)]t=0 - essendo i(0+)=i(0 -) si ha: Se il circuito è inizialmente a riposo I 0=0
 Costruzioni aerospaziali
Costruzioni aerospaziali Trasformata di laplace elettrotecnica
Trasformata di laplace elettrotecnica Obbligo manutenzione cabine elettriche
Obbligo manutenzione cabine elettriche Elementi di elettrotecnica
Elementi di elettrotecnica Reattanze impianti cogenerazione
Reattanze impianti cogenerazione Lkt elettrotecnica
Lkt elettrotecnica Ejercicios de golpe de ariete
Ejercicios de golpe de ariete Allievi vigili del fuoco
Allievi vigili del fuoco Pompe belier
Pompe belier Preparazione estiva giovanissimi 2018
Preparazione estiva giovanissimi 2018 Los invitamos a ser parte
Los invitamos a ser parte Este parte aquele parte
Este parte aquele parte Cuándo empleamos los números decimales
Cuándo empleamos los números decimales Slides para missa
Slides para missa Reti sequenziali sincrone
Reti sequenziali sincrone Scott vogler
Scott vogler Reti di calcolatori e internet
Reti di calcolatori e internet Reti di calcolatori unibo
Reti di calcolatori unibo Reti dei calcolatori
Reti dei calcolatori Jain sip
Jain sip Reti di calcolatori
Reti di calcolatori Reti di petri
Reti di petri Reti dei calcolatori
Reti dei calcolatori Metodo chou fasman
Metodo chou fasman Le reti informatiche slide
Le reti informatiche slide Monitoring troubleshooting apparati reti
Monitoring troubleshooting apparati reti Reti di calcolatori polito
Reti di calcolatori polito Italgas reti
Italgas reti Reti
Reti Reti som
Reti som Progettazione rete lan
Progettazione rete lan Slide corso ponteggi
Slide corso ponteggi Corso generale sicurezza sul lavoro
Corso generale sicurezza sul lavoro Questionario carroponte
Questionario carroponte Slide corso macchine movimento terra
Slide corso macchine movimento terra Slide corso gru mobili
Slide corso gru mobili Corso valutazione investimenti
Corso valutazione investimenti