CONJUNTO DE NMEROS COMPLEJOS NO OLVIDES APRETAR F

CONJUNTO DE NÚMEROS COMPLEJOS NO OLVIDES APRETAR F 5 PARA VER EL PPT CON LOS EFECTOS Y ANIMACIONES Profesora Patricia Romero Ulloa Mackarena Mora NO IMPRIMAS este material.

RECORDEMOS ALGUNAS COSAS

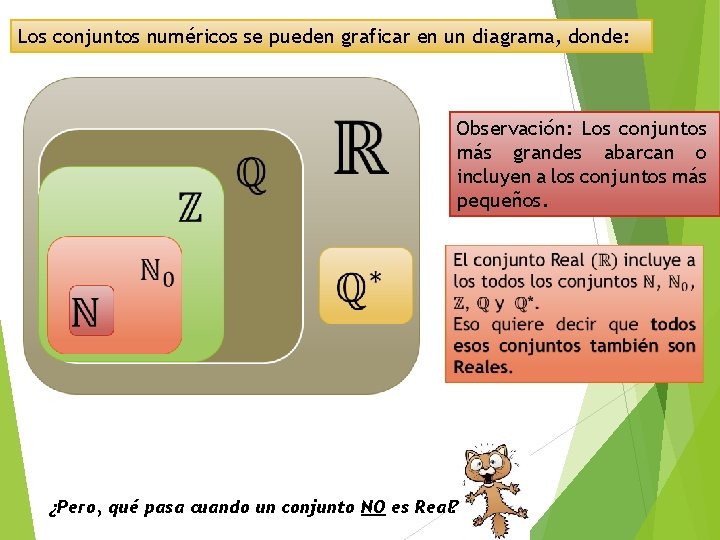
Los conjuntos numéricos se pueden graficar en un diagrama, donde: Observación: Los conjuntos más grandes abarcan o incluyen a los conjuntos más pequeños. ¿Pero, qué pasa cuando un conjunto NO es Real?

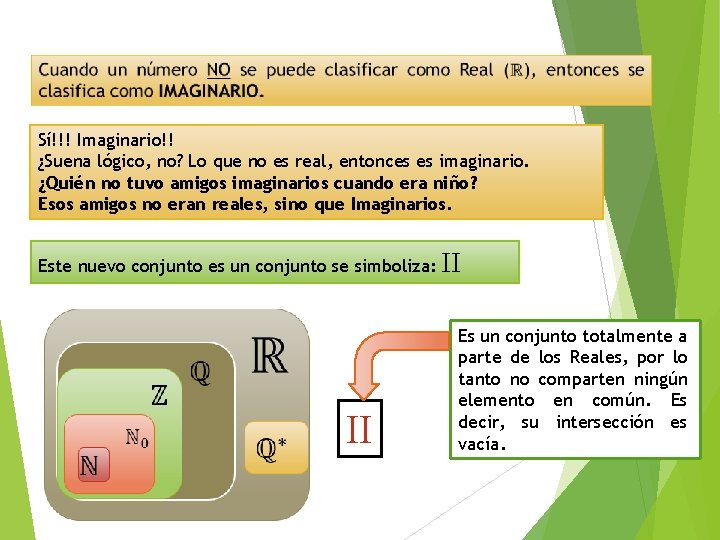
Sí!!! Imaginario!! ¿Suena lógico, no? Lo que no es real, entonces es imaginario. ¿Quién no tuvo amigos imaginarios cuando era niño? Esos amigos no eran reales, sino que Imaginarios. Este nuevo conjunto es un conjunto se simboliza: II II Es un conjunto totalmente a parte de los Reales, por lo tanto no comparten ningún elemento en común. Es decir, su intersección es vacía.

HASTA AQUÍ TODO BIEN… ENTONCES SIGAMOS

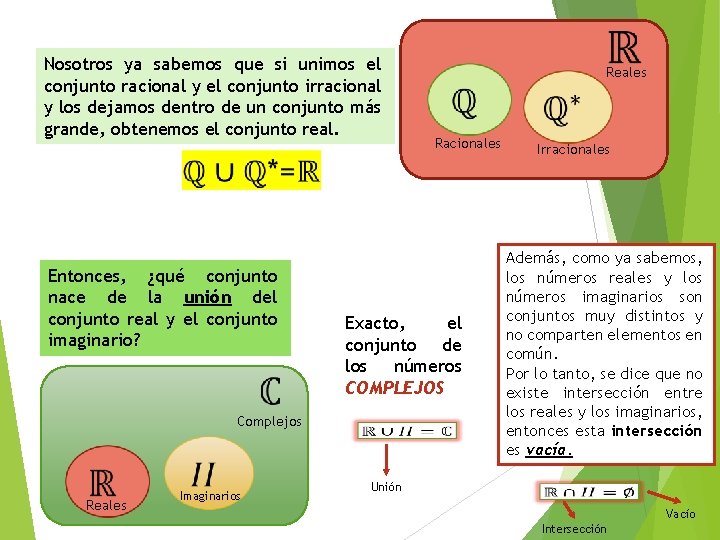
Nosotros ya sabemos que si unimos el conjunto racional y el conjunto irracional y los dejamos dentro de un conjunto más grande, obtenemos el conjunto real. Racionales Entonces, ¿qué conjunto nace de la unión del conjunto real y el conjunto imaginario? Complejos Reales Exacto, el conjunto de los números COMPLEJOS Imaginarios Unión Reales Irracionales Además, como ya sabemos, los números reales y los números imaginarios son conjuntos muy distintos y no comparten elementos en común. Por lo tanto, se dice que no existe intersección entre los reales y los imaginarios, entonces esta intersección es vacía. Vacío Intersección

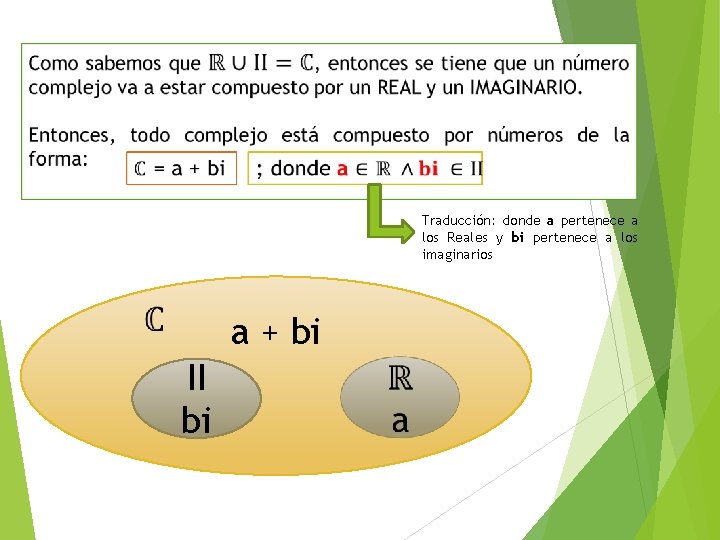
Traducción: donde a pertenece a los Reales y bi pertenece a los imaginarios a + bi II bi

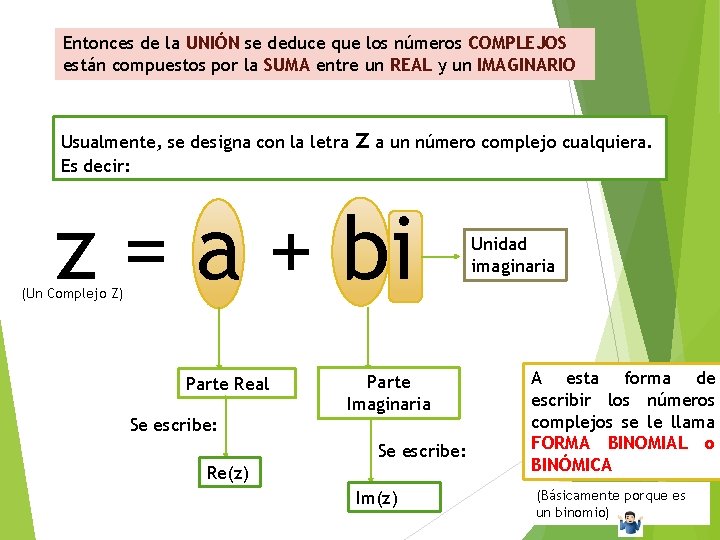
Entonces de la UNIÓN se deduce que los números COMPLEJOS están compuestos por la SUMA entre un REAL y un IMAGINARIO Usualmente, se designa con la letra Es decir: z a un número complejo cualquiera. z = a + bi Unidad imaginaria (Un Complejo Z) Parte Real Se escribe: Parte Imaginaria Se escribe: Re(z) Im(z) A esta forma de escribir los números complejos se le llama FORMA BINOMIAL o BINÓMICA (Básicamente porque es un binomio)

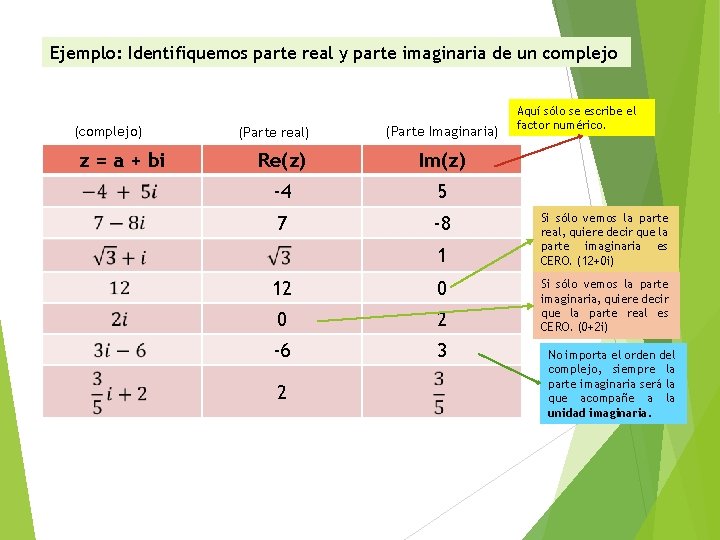
Ejemplo: Identifiquemos parte real y parte imaginaria de un complejo (complejo) z = a + bi (Parte real) (Parte Imaginaria) Re(z) Im(z) -4 5 7 -8 1 12 0 0 2 -6 3 2 Aquí sólo se escribe el factor numérico. Si sólo vemos la parte real, quiere decir que la parte imaginaria es CERO. (12+0 i) Si sólo vemos la parte imaginaria, quiere decir que la parte real es CERO. (0+2 i) No importa el orden del complejo, siempre la parte imaginaria será la que acompañe a la unidad imaginaria.

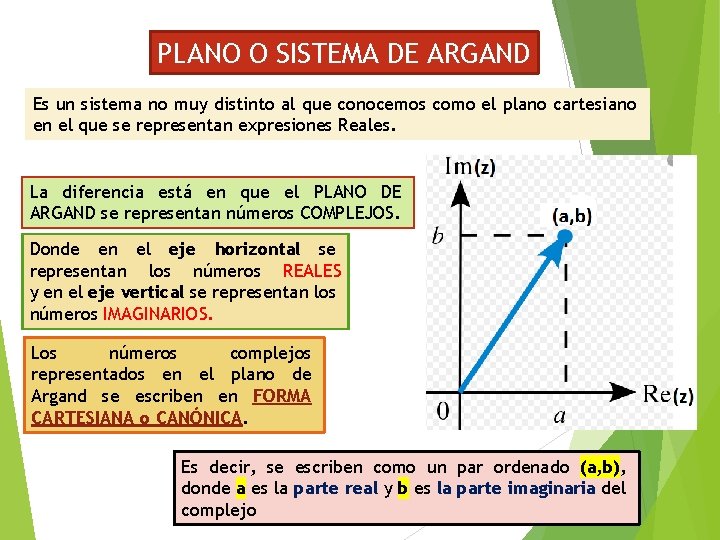
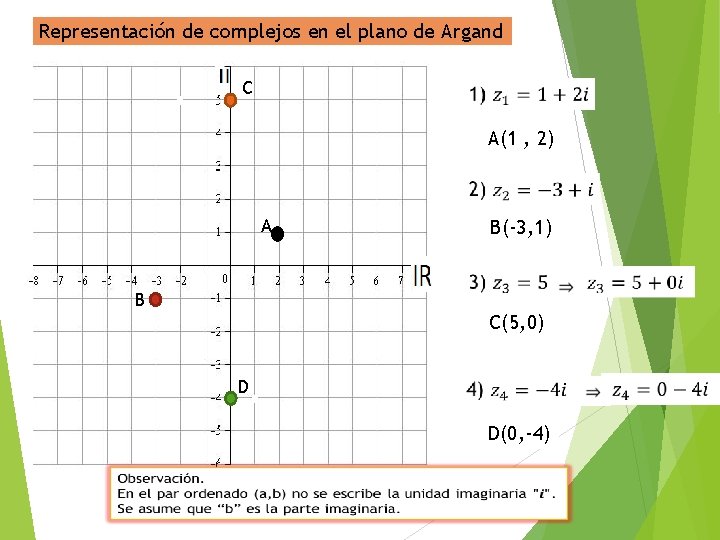
PLANO O SISTEMA DE ARGAND Es un sistema no muy distinto al que conocemos como el plano cartesiano en el que se representan expresiones Reales. La diferencia está en que el PLANO DE ARGAND se representan números COMPLEJOS. Donde en el eje horizontal se representan los números REALES y en el eje vertical se representan los números IMAGINARIOS. Los números complejos representados en el plano de Argand se escriben en FORMA CARTESIANA o CANÓNICA. Es decir, se escriben como un par ordenado (a, b), donde a es la parte real y b es la parte imaginaria del complejo

Representación de complejos en el plano de Argand C A(1 , 2) A B(-3, 1) B C(5, 0) D D(0, -4)

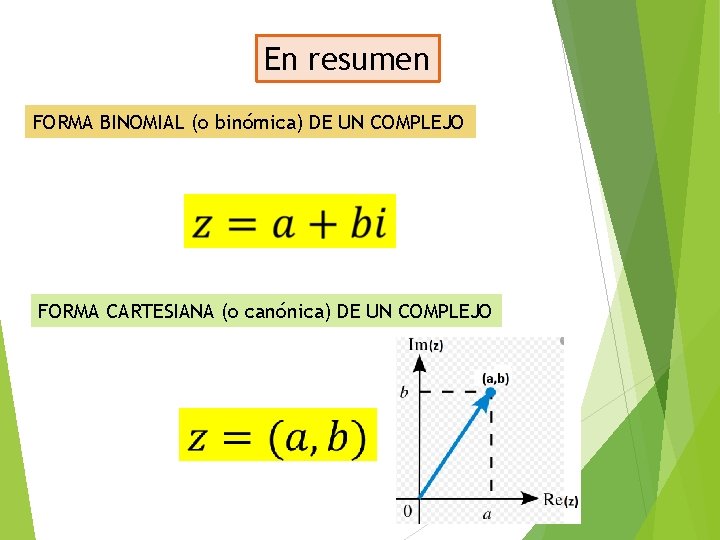
En resumen FORMA BINOMIAL (o binómica) DE UN COMPLEJO FORMA CARTESIANA (o canónica) DE UN COMPLEJO

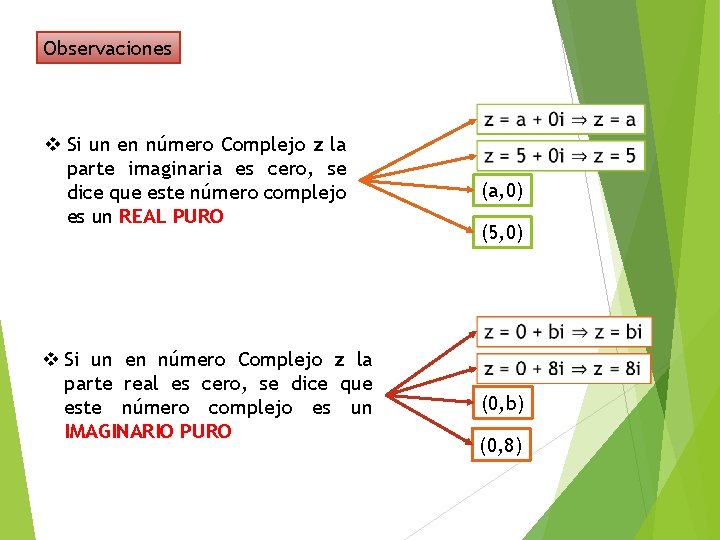
Observaciones v Si un en número Complejo z la parte imaginaria es cero, se dice que este número complejo es un REAL PURO (a, 0) (5, 0) v Si un en número Complejo z la parte real es cero, se dice que este número complejo es un IMAGINARIO PURO (0, b) (0, 8)

¡¡Ahora, a hacer la actividad!! Abre el archivo “Control Números complejos definición”, que contiene las instrucciones de lo que debes hacer. Te sugiero ver estos video tutoriales para reforzar el contenido 1) https: //www. youtube. com/watch? v=Lqy. Brrgm. Iro Complejos concepto 2) https: //www. youtube. com/watch? v=et. Ecxxis. Oh. Q Forma binomial 3) https: //www. youtube. com/watch? v=a. Qvmm. WQl. NZY Gráfica y forma cartesiana OJO!! EN EL VIDEO 1 Y 2 HAY UNOS ERRORES (Mínimos. Nadie es perfecto) ESCONDIDOS EN LA EXPLICACIÓN. SI LOS ENCUENTRAS TENDRÁS PUNTAJE ADICIONAL. MÁNDAME UN CORREO MENCIONANDO CUÁLES SON LOS ERRORES, EN QUÉ MOMENTO DEL VIDEO ESTÁN Y POR QUÉ CONSIDERAS QUE SON ERRORES. (Sólo al correo, no aceptaré respuestas por otro medio. )