Profesora Patricia Romero Ulloa NO OLVIDES APRETAR F

Profesora Patricia Romero Ulloa NO OLVIDES APRETAR F 5 PARA VER EL PPT CON LOS EFECTOS Y ANIMACIONES NO IMPRIMAS este material.

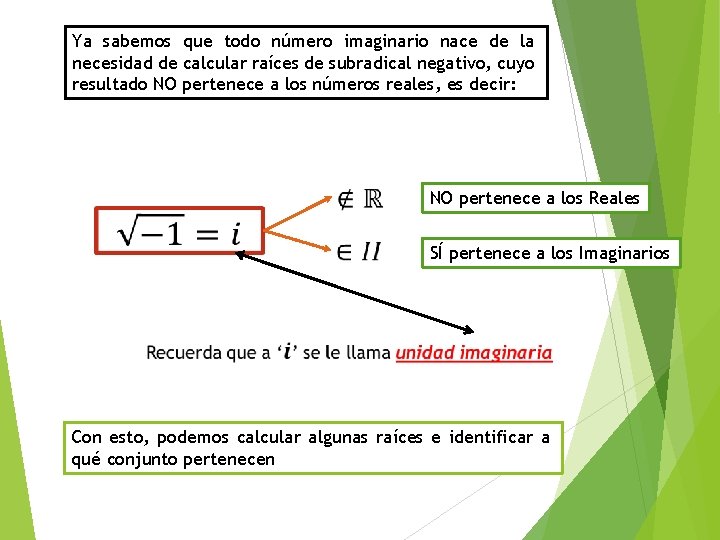
Ya sabemos que todo número imaginario nace de la necesidad de calcular raíces de subradical negativo, cuyo resultado NO pertenece a los números reales, es decir: NO pertenece a los Reales SÍ pertenece a los Imaginarios Con esto, podemos calcular algunas raíces e identificar a qué conjunto pertenecen

En general, si a es un número real positivo, se tiene: Donde i se le llama unidad imaginaria. Por ejemplo: 1) 2)

Más ejemplos!!! 3) 4) Ya estás listo(a) para calcular raíces imaginarias por ti mismo(a) ^^ Intenta hacerlas de nuevo por tu cuenta

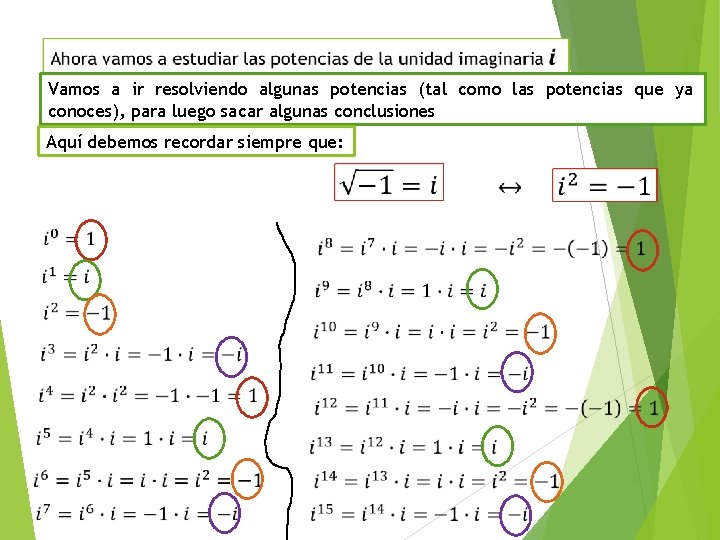
Vamos a ir resolviendo algunas potencias (tal como las potencias que ya conoces), para luego sacar algunas conclusiones Aquí debemos recordar siempre que:

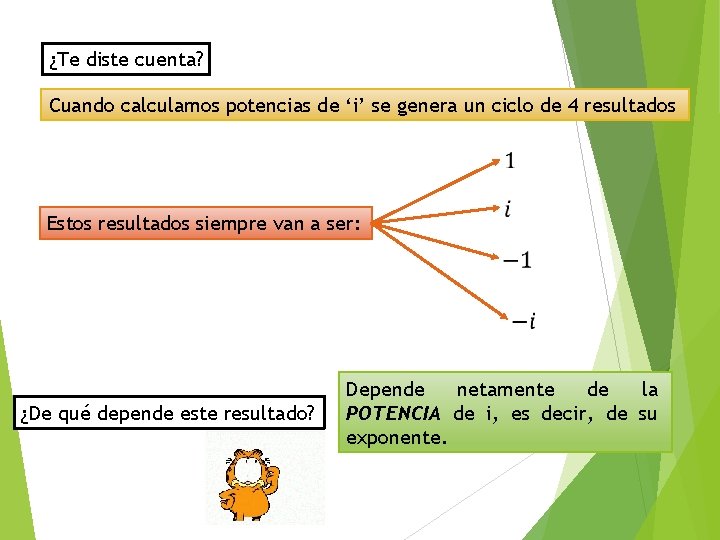
¿Te diste cuenta? Cuando calculamos potencias de ‘i’ se genera un ciclo de 4 resultados Estos resultados siempre van a ser: ¿De qué depende este resultado? Depende netamente de la POTENCIA de i, es decir, de su exponente.

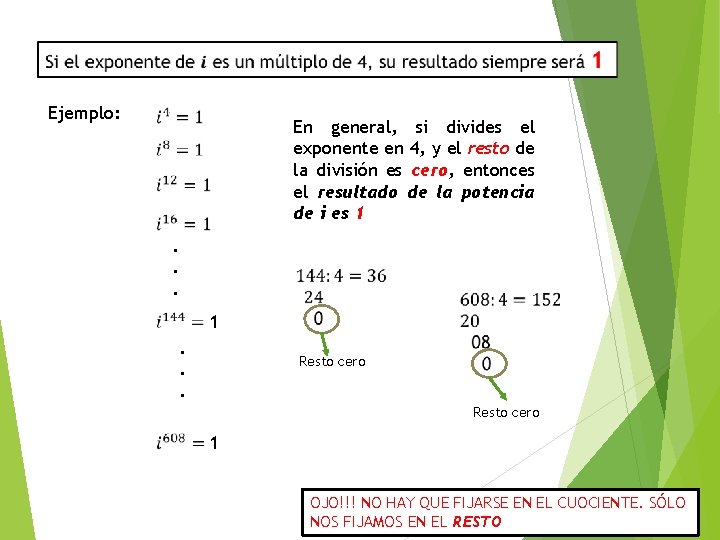
Ejemplo: En general, si divides el exponente en 4, y el resto de la división es cero, entonces el resultado de la potencia de i es 1. . . Resto cero 1 OJO!!! NO HAY QUE FIJARSE EN EL CUOCIENTE. SÓLO NOS FIJAMOS EN EL RESTO

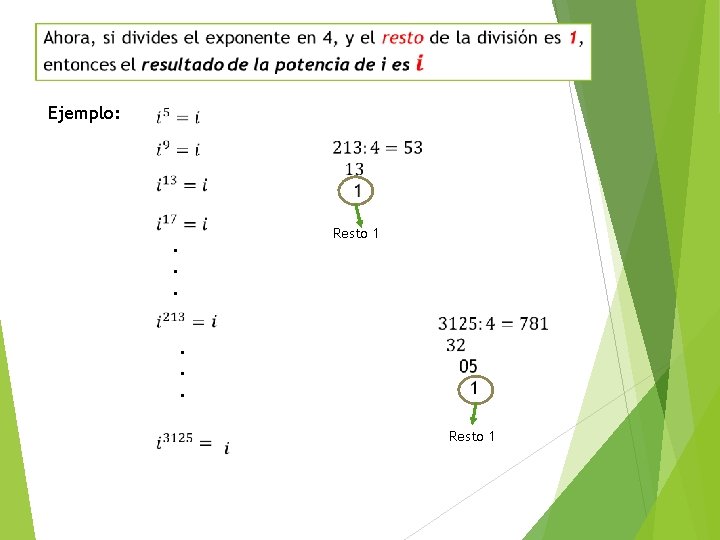
Ejemplo: Resto 1 . . . Resto 1

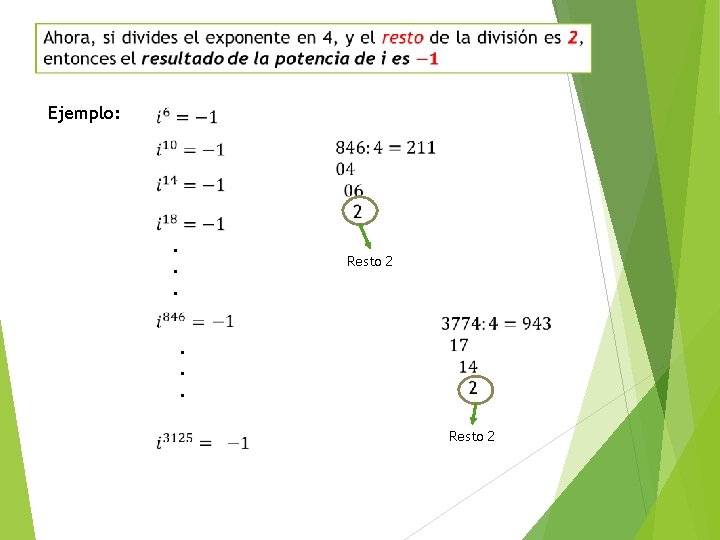
Ejemplo: . . . Resto 2 . . . Resto 2

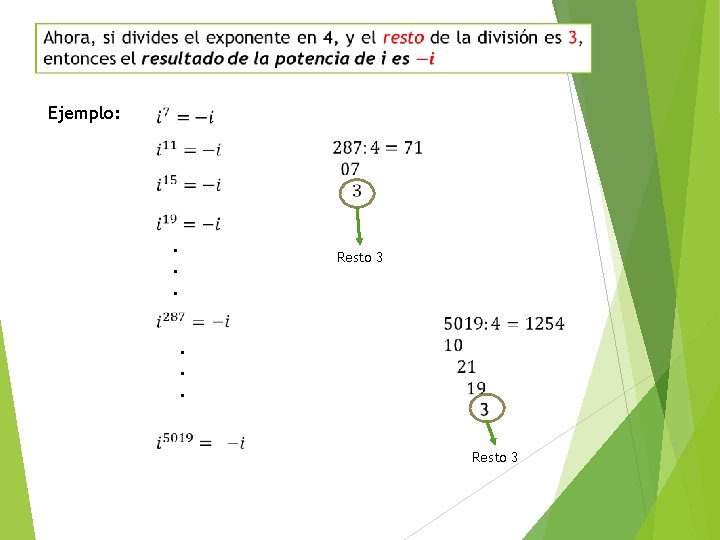
Ejemplo: . . . Resto 3

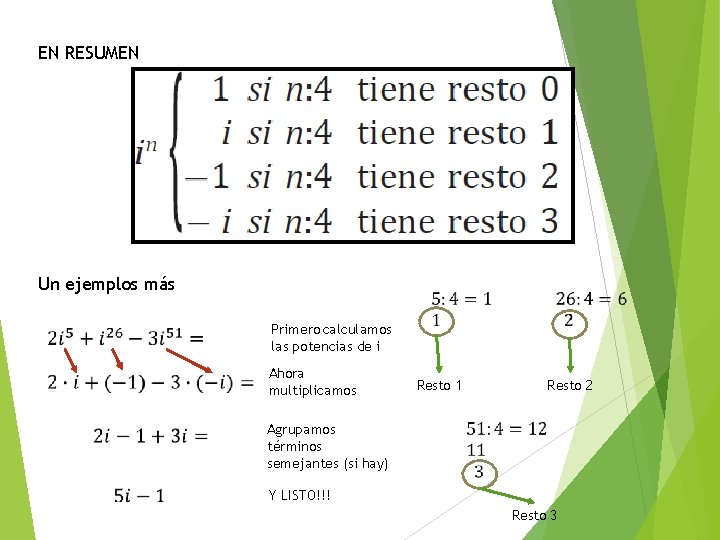
EN RESUMEN Un ejemplos más Primero calculamos las potencias de i Ahora multiplicamos Resto 1 Resto 2 Agrupamos términos semejantes (si hay) Y LISTO!!! Resto 3

¡¡Ahora, a hacer la actividad!! Abre el archivo “Control potencias de i”, que contiene las instrucciones de lo que debes hacer. Te sugiero ver estos video tutoriales que explica las potencias de i https: //www. youtube. com/watch? v=Aix. Jo. Pc. A-Bk https: //www. youtube. com/watch? v=o 0 SOLSEUSJk