Condensation inof Networks Jae Dong Noh NSPCS 08






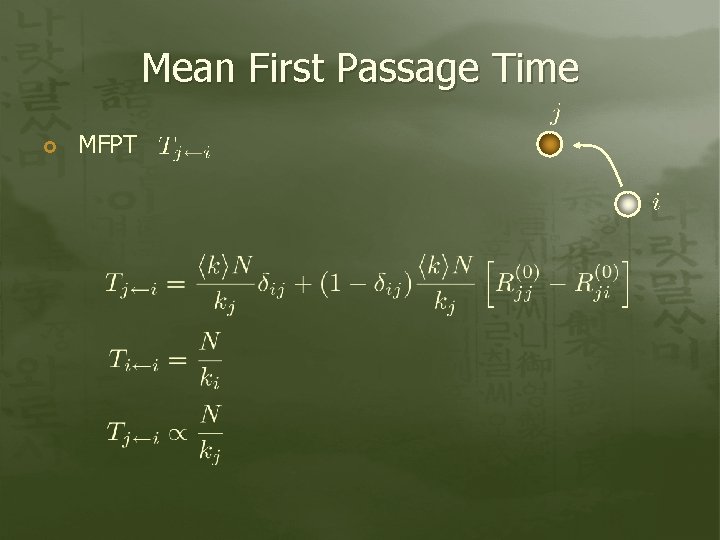


![Stationary State Property [M. R. Evans, Braz. J. Phys. 30, 42 (2000)] Stationary state Stationary State Property [M. R. Evans, Braz. J. Phys. 30, 42 (2000)] Stationary state](https://slidetodoc.com/presentation_image_h2/553466e2b876dcf115a0e519336718f7/image-14.jpg)





![dynamic instability Numerical Data for kmax [N=1000, <k>=4] linear growth dynamic phase transition sub-linear dynamic instability Numerical Data for kmax [N=1000, <k>=4] linear growth dynamic phase transition sub-linear](https://slidetodoc.com/presentation_image_h2/553466e2b876dcf115a0e519336718f7/image-23.jpg)




- Slides: 35

Condensation in/of Networks Jae Dong Noh NSPCS 08, 1 -4 July, 2008, KIAS

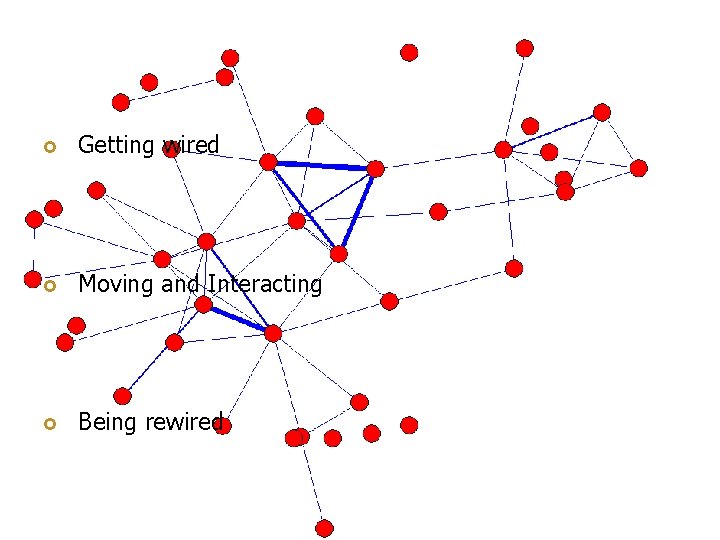
Getting wired Moving and Interacting Being rewired

References Random walks Noh and Rieger, PRL 92, 118701 (2004). Noh and Kim, JKPS 48, S 202 (2006). Zero-range processes Noh, Shim, and Lee, PRL 94, 198701 (2005). Noh, PRE 72, 056123 (2005). Noh, JKPS 50, 327 (2007). Coevolving networks Kim and Noh, PRL 100, 118702 (2008). Kim and Noh, in preparation (2008).

Networks

Basic Concepts Network = {nodes} [ {links} Adjacency matrix A Degree of a node i : Degree distribution Scale-free networks :

Random Walks

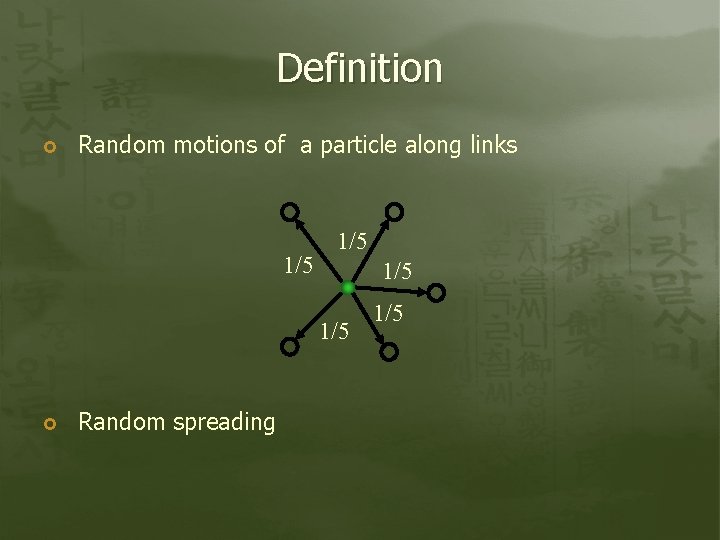
Definition Random motions of a particle along links 1/5 1/5 Random spreading 1/5

Stationary State Property Detailed balance : Stationary state probability distribution

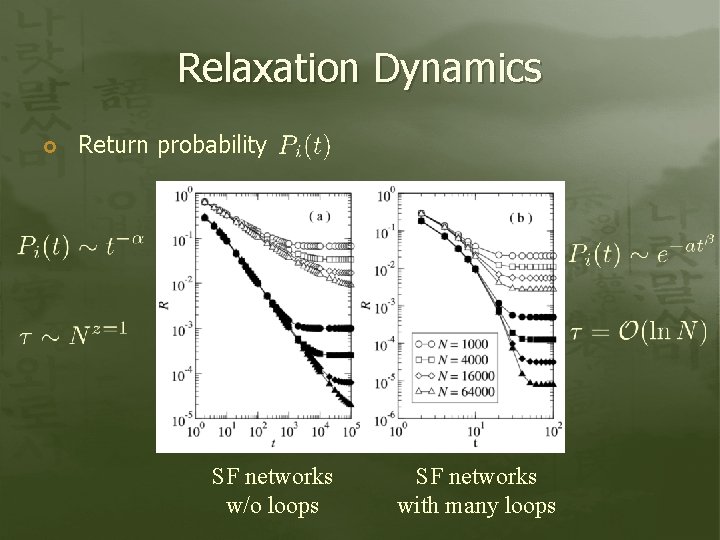
Relaxation Dynamics Return probability SF networks w/o loops SF networks with many loops
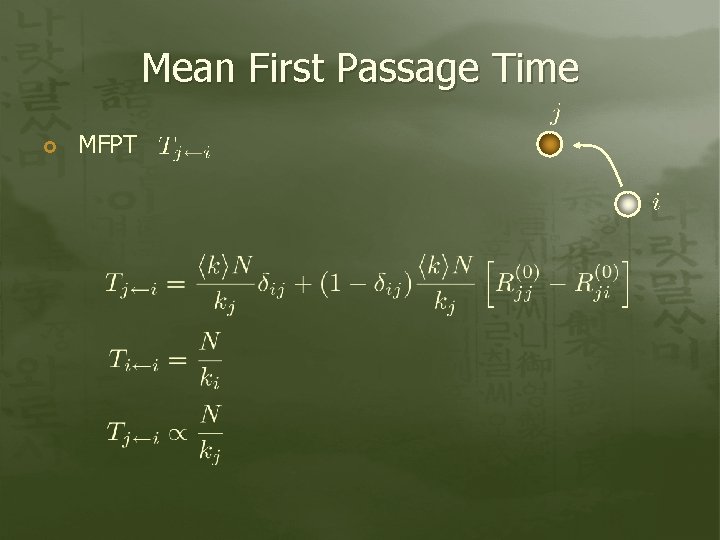
Mean First Passage Time MFPT

Zero Range Process

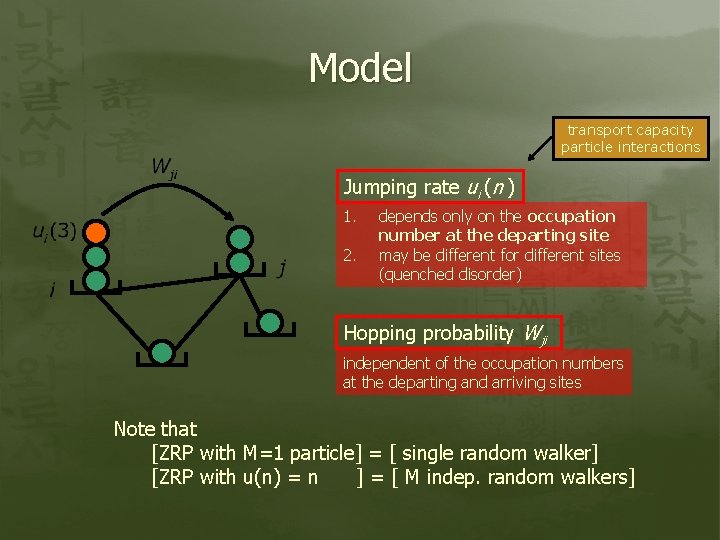
Model Interacting particle system on networks Each site may be occupied by multiple particles Dynamics : At each node i , A single particle jumps out of i at the rate ui (ni ), and hops to a neighboring node j selected randomly with the probability Wji.

Model transport capacity particle interactions Jumping rate ui (n ) 1. 2. depends only on the occupation number at the departing site. may be different for different sites (quenched disorder) Hopping probability Wji independent of the occupation numbers at the departing and arriving sites Note that [ZRP with M=1 particle] = [ single random walker] [ZRP with u(n) = n ] = [ M indep. random walkers]
![Stationary State Property M R Evans Braz J Phys 30 42 2000 Stationary state Stationary State Property [M. R. Evans, Braz. J. Phys. 30, 42 (2000)] Stationary state](https://slidetodoc.com/presentation_image_h2/553466e2b876dcf115a0e519336718f7/image-14.jpg)
Stationary State Property [M. R. Evans, Braz. J. Phys. 30, 42 (2000)] Stationary state probability distribution : product state PDF at node i : where e. g. ,

Condensation in ZRP Condensation : single (multiple) node(s) is (are) occupied by a macroscopic number of particles Condition for the condensation in lattices 1. Quenched disorder (e. g. , uimp. = <1, ui≠imp. = 1) 2. On-site attractive interaction : if the jumping rate function ui(n) = u(n) decays ‘faster’ than ~(1+2/n) e. g. ,

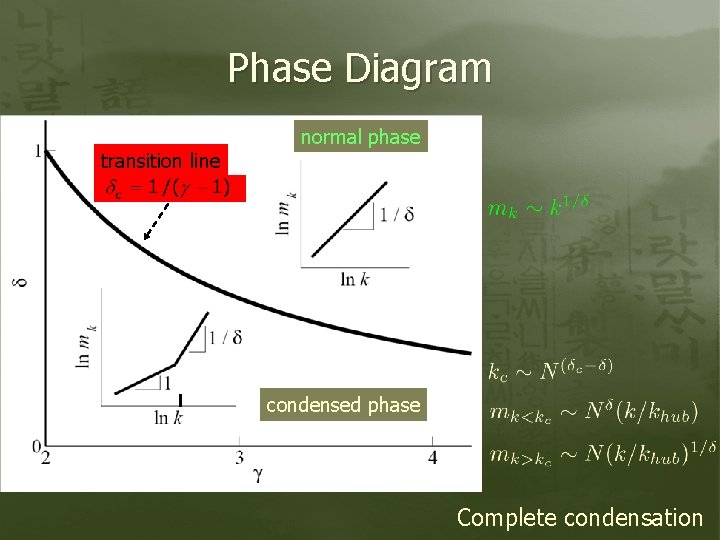
ZRP on SF Networks Scale-free networks Jumping rate (δ>1) : repulsion (δ=1) : non-interacting (δ<1) : attraction Hopping probability : random walks

Condensation on SF Networks Stationary state probability distribution Mean occupation number

Phase Diagram transition line normal phase condensed phase Complete condensation

Coevolving Networks

Synaptic Plasticity In neural networks Bio-chemical signal transmission from neural to neural through synapses Synaptic coupling strength may be enhanced (LTP) or suppressed (LTD) depending on synaptic activities Network evolution

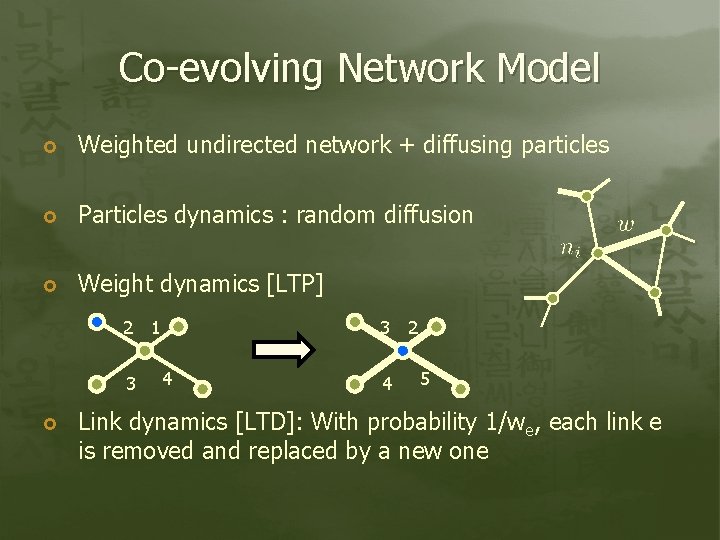
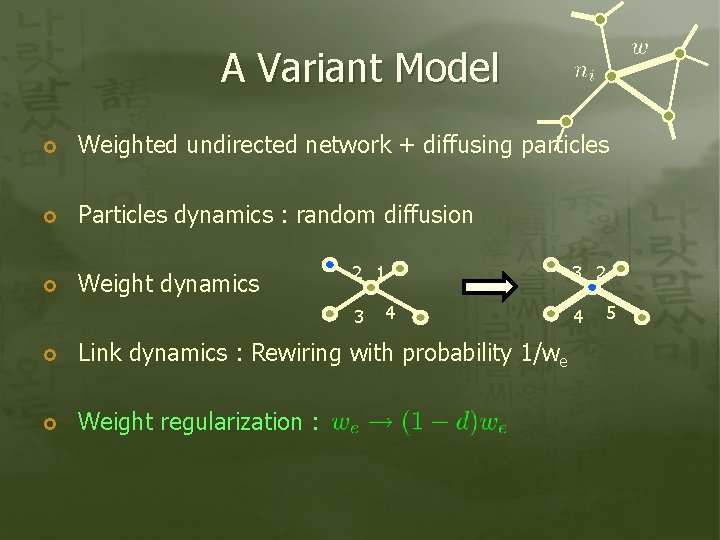
Co-evolving Network Model Weighted undirected network + diffusing particles Particles dynamics : random diffusion Weight dynamics [LTP] 2 3 1 3 4 4 2 5 Link dynamics [LTD]: With probability 1/we, each link e is removed and replaced by a new one

Dynamic Instability Due to statistical fluctuations, a node ‘hub’ may have a higher degree than others Particles tend to visit the ‘hub’ more frequently Links attached to the ‘hub’ become more robust, hence the hub collects more links than other nodes Positive feedback dynamic instability toward the formation of hubs
![dynamic instability Numerical Data for kmax N1000 k4 linear growth dynamic phase transition sublinear dynamic instability Numerical Data for kmax [N=1000, <k>=4] linear growth dynamic phase transition sub-linear](https://slidetodoc.com/presentation_image_h2/553466e2b876dcf115a0e519336718f7/image-23.jpg)
dynamic instability Numerical Data for kmax [N=1000, <k>=4] linear growth dynamic phase transition sub-linear growth

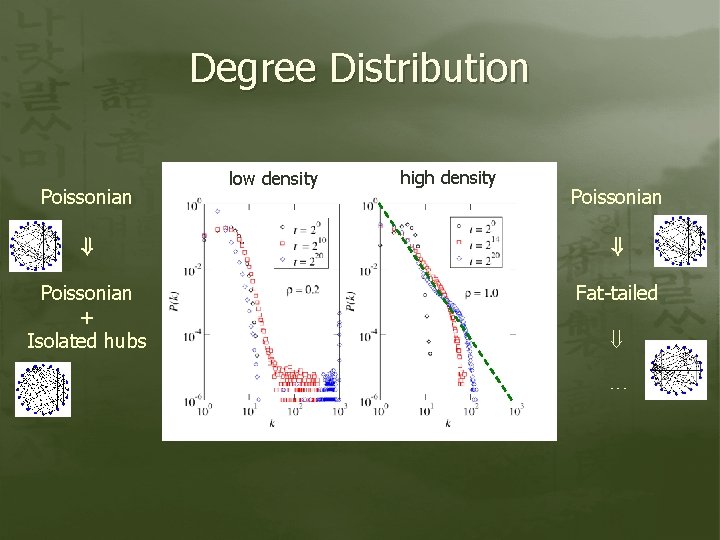
Degree Distribution Poissonian low density high density Poissonian + + Poissonian + Isolated hubs Fat-tailed

Analytic Theory Separation of time scales particle dynamics : short time scale network dynamics : long time scale Integrating out the degrees of freedom of particles Effective network dynamics : Non-Markovian queueing (balls-in-boxes) process

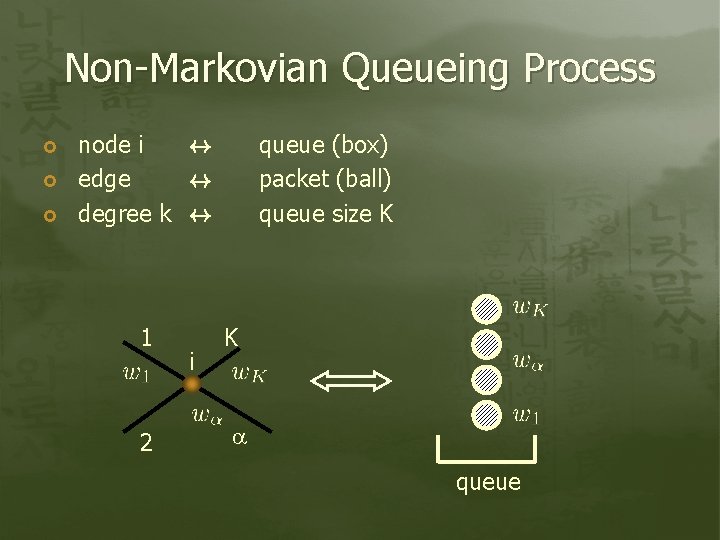
Non-Markovian Queueing Process node i $ edge $ degree k $ 1 2 i queue (box) packet (ball) queue size K K queue

Non-Markovian Queueing Process Weight of a ball A ball leaves a queue with the probability queue

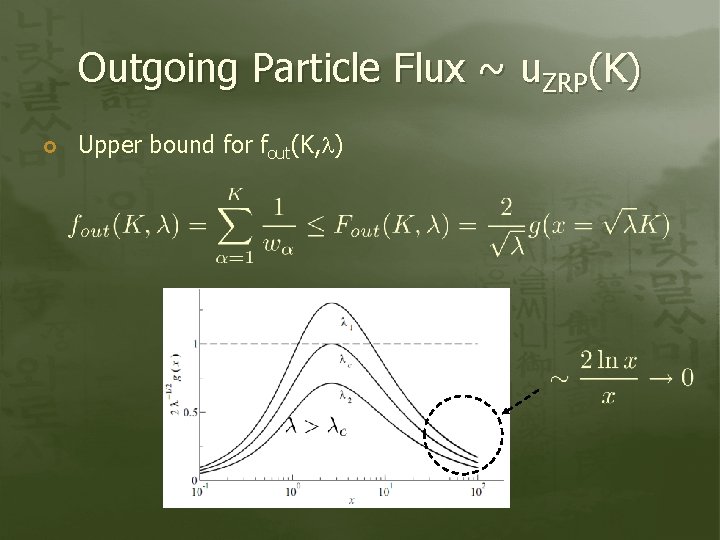
Outgoing Particle Flux ~ u. ZRP(K) Upper bound for fout(K, )

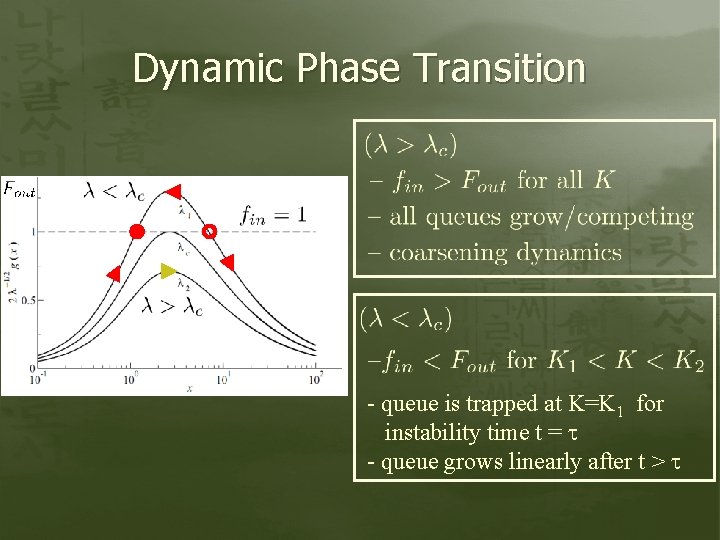
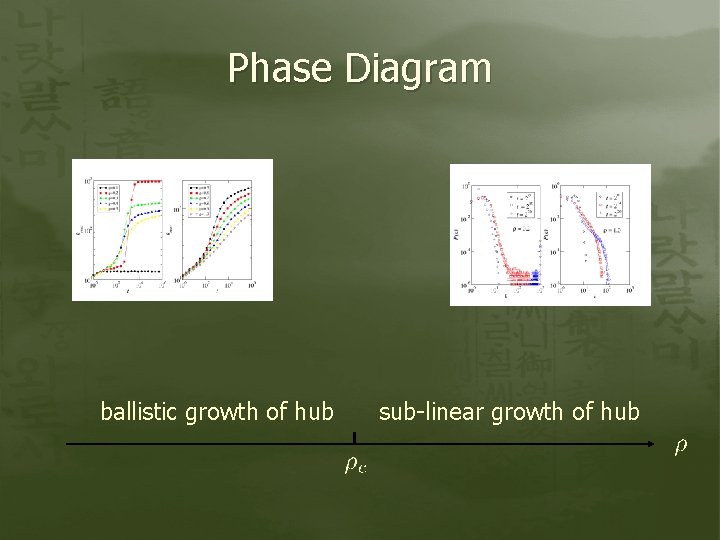
Dynamic Phase Transition - queue is trapped at K=K 1 for instability time t = - queue grows linearly after t >

Phase Diagram ballistic growth of hub sub-linear growth of hub

A Variant Model Weighted undirected network + diffusing particles Particles dynamics : random diffusion Weight dynamics 2 1 3 4 Link dynamics : Rewiring with probability 1/we Weight regularization : 3 2 4 5

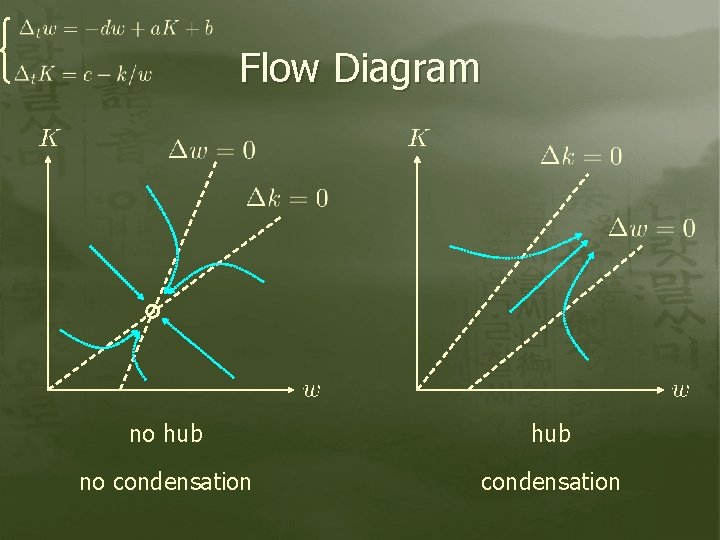
A Simplified Theory 1 2 i K potential candidate for the hub Rate equations for K and w

Flow Diagram no hub no condensation

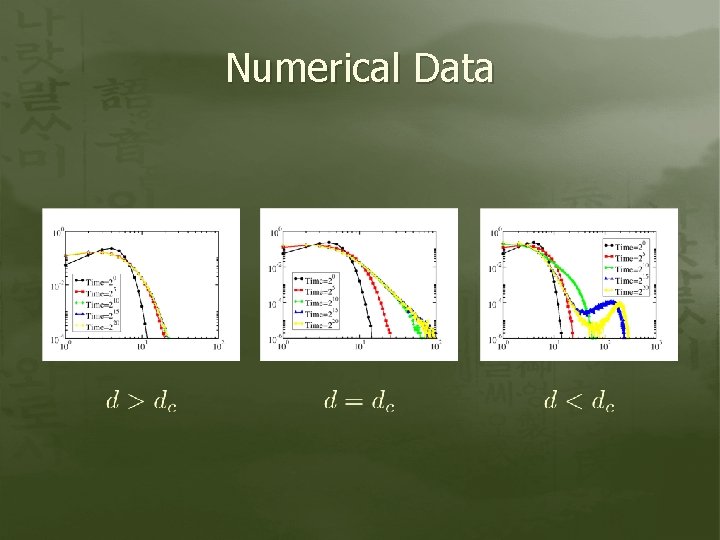
Numerical Data

Summary Dynamical systems on networks random walks zero range process Coevolving network models Network heterogeneity $ Condensation
 Jae dong noh
Jae dong noh Merrily merrily christmas bells are ringing
Merrily merrily christmas bells are ringing Noh hyungjin
Noh hyungjin Sinogram
Sinogram Japanese noh theatre
Japanese noh theatre @fauzi:http://work4unity.in/haicantik.html
@fauzi:http://work4unity.in/haicantik.html Site:slidetodoc.com
Site:slidetodoc.com Omer boyaci
Omer boyaci Jumps in assembly language
Jumps in assembly language Jae booklet 2019
Jae booklet 2019 Flow control instructions in assembly language
Flow control instructions in assembly language Jae lee columbia
Jae lee columbia Conditional jump instructions in 8086
Conditional jump instructions in 8086 Difference between virtual circuit and datagram
Difference between virtual circuit and datagram Backbone networks in computer networks
Backbone networks in computer networks Rang dong restaurant
Rang dong restaurant Yuxiao dong
Yuxiao dong Lan dong
Lan dong Debayashi
Debayashi Hoa gì
Hoa gì The le family was sleeping when mailman
The le family was sleeping when mailman Dong liu ustc
Dong liu ustc Hệ thống thông tin logistics là gì
Hệ thống thông tin logistics là gì Dong sun-hwa
Dong sun-hwa Hoa thụ phấn nhờ gió
Hoa thụ phấn nhờ gió Balbal na salita
Balbal na salita Changyu dong
Changyu dong Pooh pooh theory of language
Pooh pooh theory of language Ziqian dong
Ziqian dong We mean business
We mean business Percival zhang
Percival zhang Dong quai nedir
Dong quai nedir Luna xuan
Luna xuan Dong pei li
Dong pei li Overhanged
Overhanged Peter dong
Peter dong