Completing the Square The MEn Te Program Math





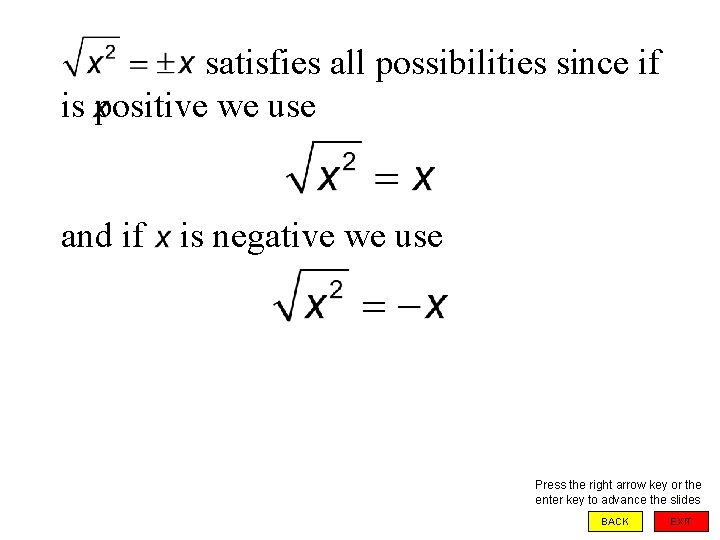








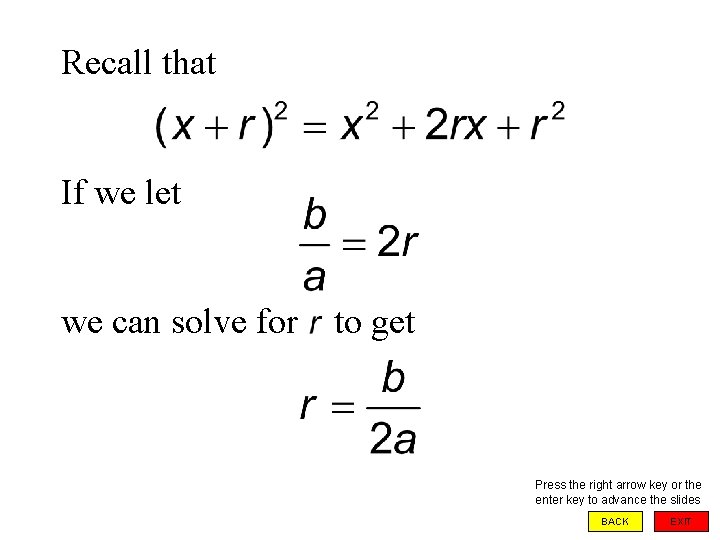




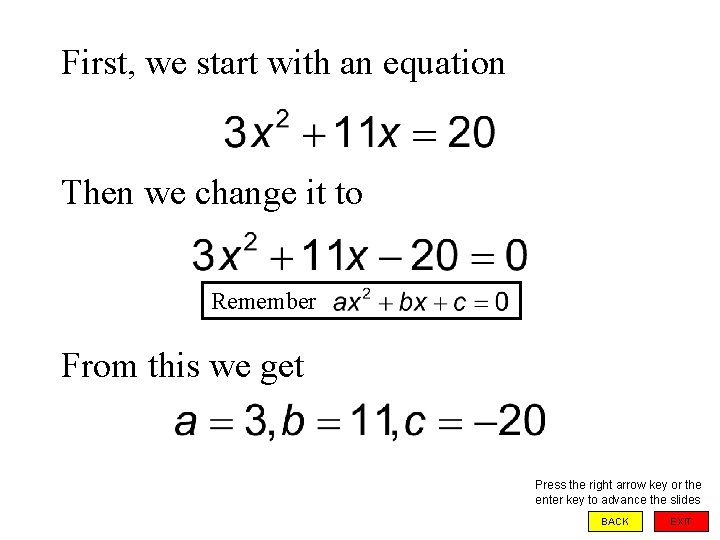


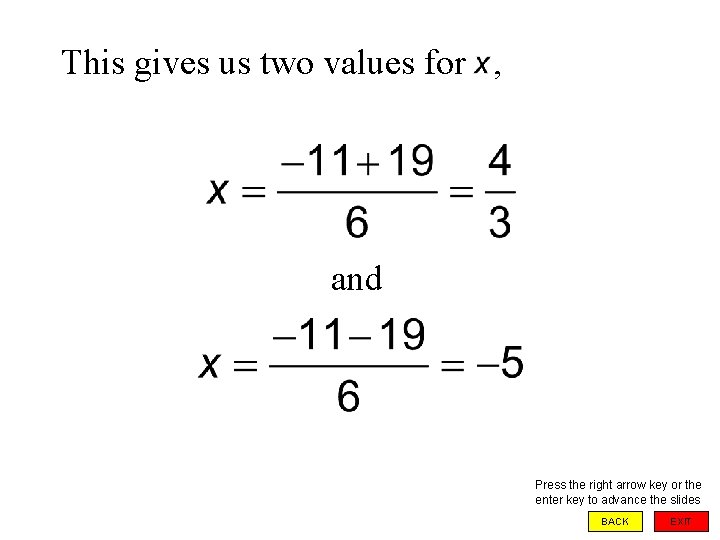






- Slides: 29

Completing the Square The MEn. Te Program Math Enrichment through Technology Title V East Los Angeles College Click one of the buttons below or press the enter key © 2003 East Los Angeles College. All rights reserved. NEXT EXIT

The easiest quadratic equations to solve are of the type where r is any constant. Press the right arrow key or the enter key to advance the slides BACK EXIT

The solution to is The answer comes from the fact that we solve the equation by taking the square root of both sides Press the right arrow key or the enter key to advance the slides BACK EXIT

Since is a constant, we get where both sides are positive, but since is a variable it could be negative, yet is positive and is also positive. Press the right arrow key or the enter key to advance the slides BACK EXIT

If we write and is negative, we are saying that a positive number is negative, which it cannot be. To get around this contradiction we need to insist that Press the right arrow key or the enter key to advance the slides BACK EXIT
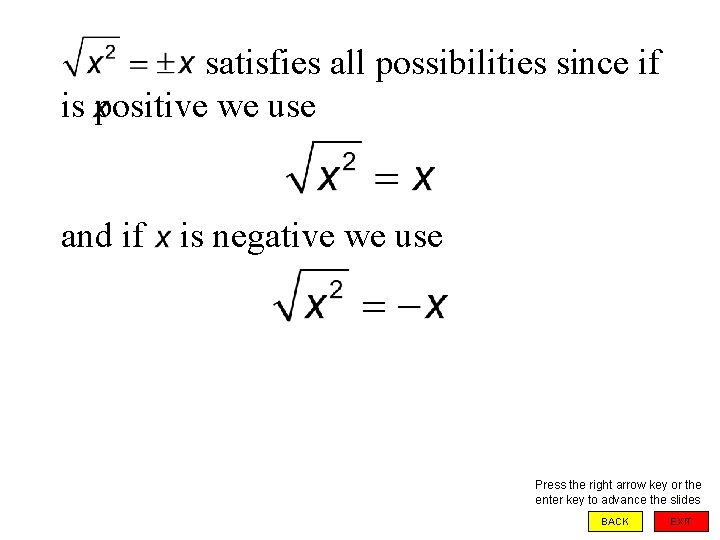
satisfies all possibilities since if is positive we use and if is negative we use Press the right arrow key or the enter key to advance the slides BACK EXIT

Thus, we get the solution for We generally change this equation by multiplying both sides by , then we simplify and get Press the right arrow key or the enter key to advance the slides BACK EXIT

We generally skip all the intermediate steps for an equation like and get Press the right arrow key or the enter key to advance the slides BACK EXIT

For quadratic equations such as we solve and get Press the right arrow key or the enter key to advance the slides BACK EXIT

For quadratic equations that are not expressed as an equation between two squares, we can always express them as If this equation can be factored, then it can generally be solved easily. Press the right arrow key or the enter key to advance the slides BACK EXIT

If the equation can be put in the form then we can use the square root method described previously to solve it. The solution for this equation is The sign of m needs to be the opposite of the sign used in Press the right arrow key or the enter key to advance the slides BACK EXIT

The question becomes: “Can we change the equation from the form to the form ? ” Fortunately the answer is yes! Press the right arrow key or the enter key to advance the slides BACK EXIT

The procedure for changing is as follows. First, divide by , this gives Then subtract gives from both sides. This Press the right arrow key or the enter key to advance the slides BACK EXIT

We pause at this point to review the process of squaring a binomial. We will use this procedure to help us complete the square. Press the right arrow key or the enter key to advance the slides BACK EXIT
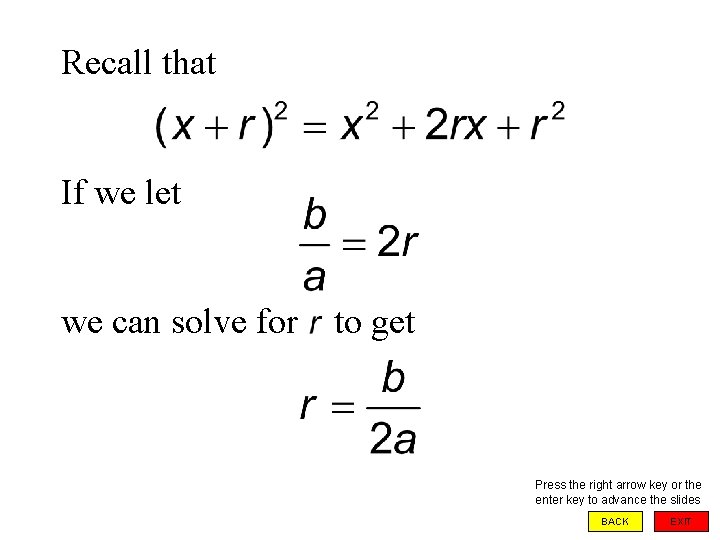
Recall that If we let we can solve for to get Press the right arrow key or the enter key to advance the slides BACK EXIT

Substituting we get in Using the symmetric property of equations to reverse this equation we get Press the right arrow key or the enter key to advance the slides BACK EXIT

Now we will return to where we left our original equation. If we add we get or to both sides of Press the right arrow key or the enter key to advance the slides BACK EXIT

We can now solve this by taking the square root of both sides to get Press the right arrow key or the enter key to advance the slides BACK EXIT

is known as the quadratic formula. It is used to solve any quadratic equation in one variable. We will show the quadratic equation is used in the example that follows. Press the right arrow key or the enter key to advance the slides BACK EXIT
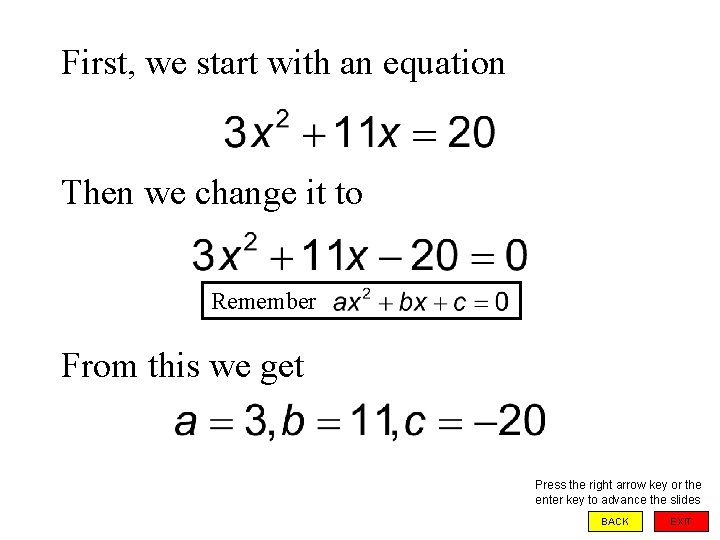
First, we start with an equation Then we change it to Remember From this we get Press the right arrow key or the enter key to advance the slides BACK EXIT

We then substitute into the quadratic formula, simplify and get our values for. Press the right arrow key or the enter key to advance the slides BACK EXIT

Doing so we get Remember the quadratic equation is and the values are a = 3, b = 11, c = -20 Press the right arrow key or the enter key to advance the slides BACK EXIT
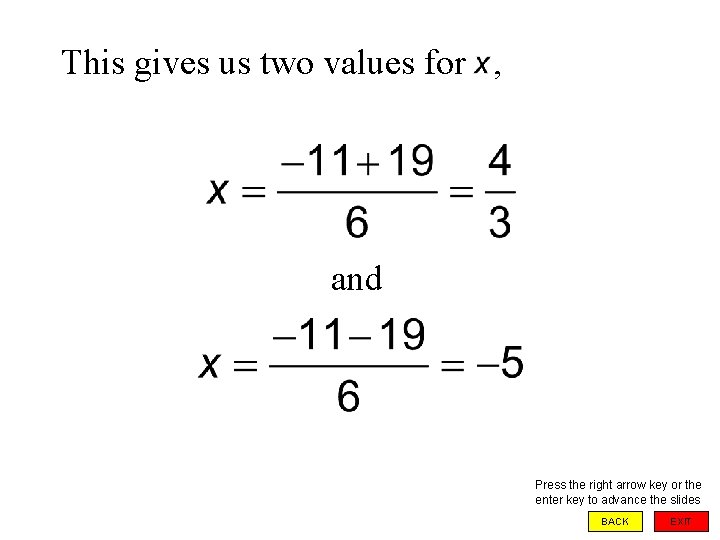
This gives us two values for , and Press the right arrow key or the enter key to advance the slides BACK EXIT

The equation can be factored into which will give us the same solutions as the quadratic formula. However, the beauty of using the quadratic formula is that it works for ALL quadratic equations, even those not factorable (and even when is negative). Press the right arrow key or the enter key to advance the slides BACK EXIT

To review—the steps in using the quadratic formula are as follows: 1. Set the equation equal to zero, being careful not to make an error in signs. Press the right arrow key or the enter key to advance the slides BACK EXIT

2. Determine the values of a, b, and c after the equation is set to zero. Remember Press the right arrow key or the enter key to advance the slides BACK EXIT

3. Substitute the values of a, b, and c into the quadratic formula. Press the right arrow key or the enter key to advance the slides BACK EXIT

4. Simplify the formula after substituting and find the solutions. Press the right arrow key or the enter key to advance the slides BACK EXIT

Contact Us At: The MEn. Te Program / Title V East Los Angeles College 1301 Avenida Cesar Chavez Monterey Park, CA 91754 Phone: (323) 265 -8784 Fax: (323) 415 -4109 Email Us At: menteprogram@yahoo. com Our Websites: http: //www. matematicamente. org http: //www. mente. elac. org Press the right arrow key or the enter key to advance the slides BACK EXIT
 Completing square program
Completing square program How to do completing the square
How to do completing the square How to complete the square
How to complete the square Completing the square solver
Completing the square solver Trinomial example
Trinomial example 4-6 completing the square
4-6 completing the square Example of completing the square
Example of completing the square Dr frost quadratic graphs
Dr frost quadratic graphs Complete square steps
Complete square steps How to find perfect square
How to find perfect square Lesson 9-1 completing the square
Lesson 9-1 completing the square Completion of squares
Completion of squares 9-7 solving quadratic equations by using square roots
9-7 solving quadratic equations by using square roots 9-5 completing the square
9-5 completing the square Completing the square (continued) quiz
Completing the square (continued) quiz 2-4 completing the square
2-4 completing the square Completing the square tutorial
Completing the square tutorial Solving quadratic equations by completing the square
Solving quadratic equations by completing the square Nat 5 parabolas
Nat 5 parabolas Completing the square formula
Completing the square formula A perfect square trinomial is a trinomial of the form
A perfect square trinomial is a trinomial of the form Dr frost differentiation
Dr frost differentiation Completing the square (continued)
Completing the square (continued) Completing the square (continued)
Completing the square (continued) Mathswatch completing the square answers
Mathswatch completing the square answers Complete the square minimum point
Complete the square minimum point Creating a perfect square trinomial
Creating a perfect square trinomial Rewrite the function by completing the square
Rewrite the function by completing the square 2-4 completing the square
2-4 completing the square Completing the square
Completing the square