Section 4 6 Completing the Square Students will































- Slides: 32

Section 4. 6 – Completing the Square Students will be able to: • To solve equations by completing the square • To rewrite functions by completing the square Lesson Vocabulary: Completing the Square

Section 4. 6 – Completing the Square

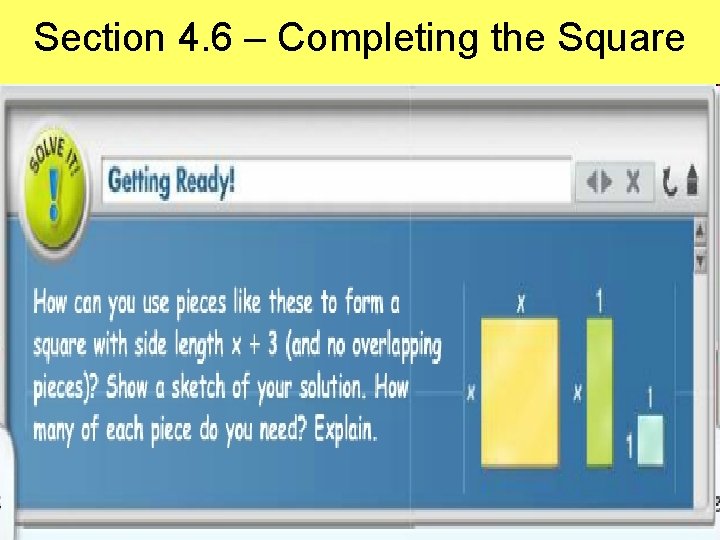
Section 4. 6 – Completing the Square Forming a square with model pieces provides a useful geometric image for completing the square algebraically. Essential Understanding: Completing a perfect square trinomial allows you to factor the completed trinomial as the square of a binomial.

Section 4. 6 – Completing the Square Problem 1: What is the solution of each equation? 4 x 2 + 10 = 46

Section 4. 6 – Completing the Square Problem 1: What is the solution of each equation? 3 x 2 – 5 = 25

Section 4. 6 – Completing the Square Problem 1: What is the solution of each equation? 7 x 2 – 10 = 25

Section 4. 6 – Completing the Square Problem 1: What is the solution of each equation? 2 x 2 + 9 = 13

Section 4. 6 – Completing the Square Problem 2: While designing a house, an architect used windows like the one shown here. What are the dimensions of the window if it has 2766 square inches of glass?

Section 4. 6 – Completing the Square Problem 3: What is the solution of x 2 + 4 x + 4 = 25?

Section 4. 6 – Completing the Square Problem 3: What is the solution of x 2 – 14 x + 49 = 25?

Section 4. 6 – Completing the Square If x 2 + bx is not part of a perfect square trinomial, you can use the coefficient b to find a constant c so that x 2 + bx + c is a perfect square. When you do this, you are completing the square.

Section 4. 6 – Completing the Square When you do this, you are completing the square.

Section 4. 6 – Completing the Square When you do this, you are completing the square.

Section 4. 6 – Completing the Square Problem 4: What value completes the square for x 2 – 10 x? Justify your answer.

Section 4. 6 – Completing the Square Problem 4: What value completes the square for x 2 + 6 x? Justify your answer.

Section 4. 6 – Completing the Square

Section 4. 6 – Completing the Square Problem 5: What is the solution of 3 x 2 – 12 x + 6 = 0?

Section 4. 6 – Completing the Square Problem 5: What is the solution of 2 x 2 – x + 3 = x + 9?

Section 4. 6 – Completing the Square You can complete a square to change a quadratic function to vertex form. Problem 6: What is y = x 2 + 4 x – 6 in vertex form? Name the vertex and y-intercept.

Section 4. 6 – Completing the Square Problem 6: What is y = x 2 + 3 x – 6 in vertex form? Name the vertex and y-intercept.

Section 4. 6 – Completing the Square Problem 6: What is y = 2 x 2 – 6 x – 1 in vertex form? Name the vertex and y-intercept.

Section 4. 6 – Completing the Square Problem 6: What is y = -x 2 + 4 x – 1 in vertex form? Name the vertex and y-intercept.

Section 4. 6 – Completing the Square EXTRA PROBLEMS: Solve the quadratic by completing the square: x 2 – x = 5

Section 4. 6 – Completing the Square EXTRA PROBLEMS: Solve the quadratic by completing the square: 2 x 2 – ½x = 1/8

Section 4. 6 – Completing the Square EXTRA PROBLEMS: Solve the quadratic by completing the square: 3 x 2 +x = 2/3

Section 4. 6 – Completing the Square EXTRA PROBLEMS: Solve the quadratic by completing the square: -. 25 x 2 – 0. 6 x + 0. 3 = 0

Section 4. 6 – Completing the Square EXTRA PROBLEMS: Solve for x in terms of a: 2 x 2 – ax = 6 a 2

Section 4. 6 – Completing the Square EXTRA PROBLEMS: Solve for x in terms of a: 6 a 2 x 2 – 11 ax = 10

Section 4. 6 – Completing the Square EXTRA PROBLEMS: Solve for x in terms of a: 4 a 2 x 2 + 8 ax + 3= 0

Section 4. 6 – Completing the Square EXTRA PROBLEMS: Solve for x in terms of a: 4 a 2 x 2 + 8 ax + 3= 0

Section 4. 6 – Completing the Square

Section 4. 6 – Completing the Square
 How to do completing the square
How to do completing the square Site:slidetodoc.com
Site:slidetodoc.com Quadratic formula complete the square
Quadratic formula complete the square Completing the square examples
Completing the square examples 4-6 completing the square
4-6 completing the square Quadratic function examples with answers
Quadratic function examples with answers Quadratic equations gcse
Quadratic equations gcse Complete the square examples
Complete the square examples Completing the square steps
Completing the square steps 9-5 solving quadratic equations by completing the square
9-5 solving quadratic equations by completing the square Completion of squares
Completion of squares Completing the square (continued) quiz
Completing the square (continued) quiz 9-5 completing the square
9-5 completing the square Lesson 8-8 practice b completing the square answers
Lesson 8-8 practice b completing the square answers Completing the square (continued) quiz
Completing the square (continued) quiz Completing the square tutorial
Completing the square tutorial Equation for completing the square
Equation for completing the square Nature of roots nat 5
Nature of roots nat 5 Completing the square formula
Completing the square formula Example of trinomial
Example of trinomial Dr frost maths differentiation
Dr frost maths differentiation Completing square program
Completing square program 4-5 completing the square answers
4-5 completing the square answers Completing the square (continued)
Completing the square (continued) Mathswatch solver
Mathswatch solver Completing the square
Completing the square Perfect squares factoring
Perfect squares factoring Completing the square vs quadratic formula
Completing the square vs quadratic formula 2-4 completing the square
2-4 completing the square Completing the square
Completing the square 9-8 completing the square
9-8 completing the square Completing square
Completing square Missing term perfect square trinomial calculator
Missing term perfect square trinomial calculator