Nuffield FreeStanding Mathematics Activity Completing the square Nuffield




- Slides: 7

Nuffield Free-Standing Mathematics Activity Completing the square © Nuffield Foundation 2011

Completing the square means writing the unknown terms of a quadratic in a square bracket Example because Application To find the maximum or minimum value of this function. Think about… What is always true about the value of (x + 3)2? What will always be true for (x + 3)2 – 2? Minimum value of is – 2

Application To find the minimum point on the graph of the function. Think about… For what value of x is (x + 3)2 – 2 a minimum? has a minimum value when x = – 3 Minimum point on the curve is (– 3 , – 2) Think about… What shape is the graph of y = x 2 + 6 x + 7 ? Can completing the square help you sketch the graph of a quadratic?

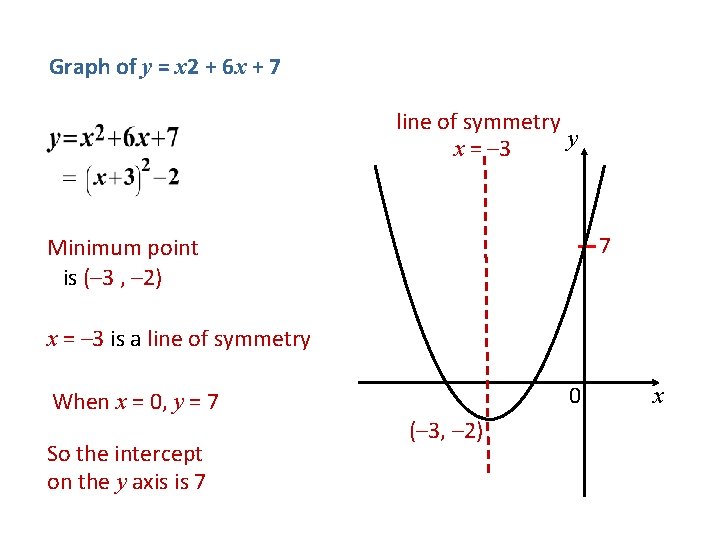
Graph of y = x 2 + 6 x + 7 line of symmetry y x = – 3 7 Minimum point is (– 3 , – 2) x = – 3 is a line of symmetry When x = 0, y = 7 So the intercept on the y axis is 7 0 (– 3, – 2) x

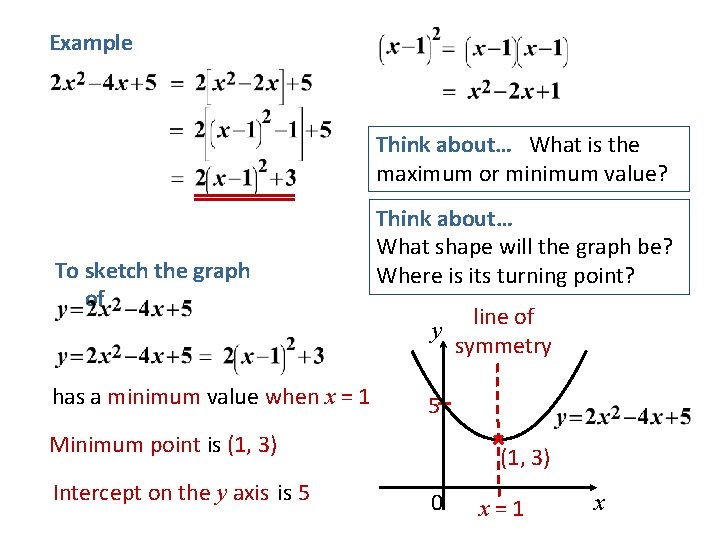
Example Think about… What is the maximum or minimum value? To sketch the graph of Think about… What shape will the graph be? Where is its turning point? y has a minimum value when x = 1 5 Minimum point is (1, 3) Intercept on the y axis is 5 line of symmetry (1, 3) 0 x=1 x

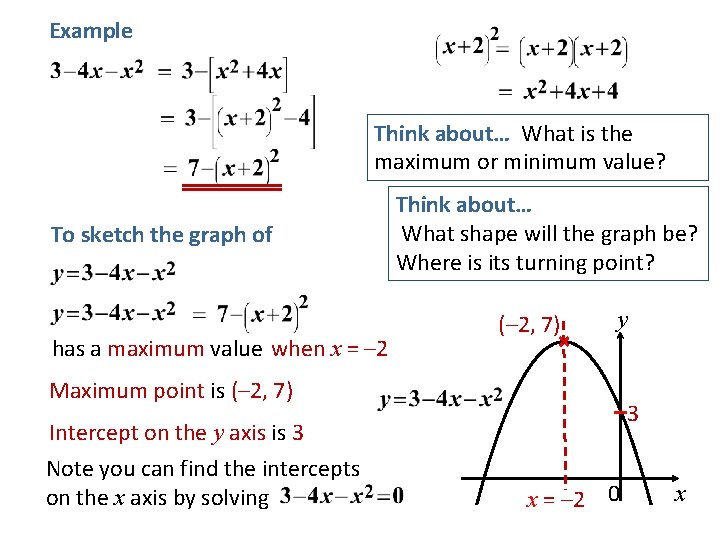
Example Think about… What is the maximum or minimum value? To sketch the graph of has a maximum value when x = – 2 Think about… What shape will the graph be? Where is its turning point? (– 2, 7) y Maximum point is (– 2, 7) 3 Intercept on the y axis is 3 Note you can find the intercepts on the x axis by solving x = – 2 0 x

Completing the square Reflect on your work How does completing the square help you to sketch the graph of the function? Can you use completing the square to tell you whether the quadratic function has any real roots?













