Completing the Square Objective To complete a square

Completing the Square • Objective: To complete a square for a quadratic equation and solve by completing the square

Steps to complete the square • 1. ) You will get an expression that looks like this: AX²+ BX • 2. ) Our goal is to make a square such that we have (a + b)² = a² +2 ab + b² • 3. ) We take ½ of the X coefficient (Divide the number in front of the X by 2) • 4. ) Then square that number

To Complete the Square x 2 + 6 x • Take half of the coefficient of ‘x’ 3 • Square it and add it 9 x 2 + 6 x + 9 = (x + 3)2

Complete the square, and show what the perfect square is:

To solve by completing the square • If a quadratic equation does not factor we can solve it by two different methods • 1. ) Completing the Square (today’s lesson) • 2. ) Quadratic Formula (Next week’s lesson)

Steps to solve by completing the square 1. ) If the quadratic does not factor, move the constant to the other side of the equation Ex: x²-4 x -7 =0 x²-4 x=7 2. ) Work with the x²+ x side of the equation and complete the square by taking ½ of the coefficient of x and squaring Ex. x² -4 x 4/2= 2²=4 3. ) Add the number you got to complete the square to both sides of the equation Ex: x² -4 x +4 = 7 +4 4. )Simplify your trinomial square Ex: (x-2)² =11 5. )Take the square root of both sides of the equation Ex: x-2 =±√ 11 6. ) Solve for x Ex: x=2±√ 11

Solve by Completing the Square +9 +9

Solve by Completing the Square +121

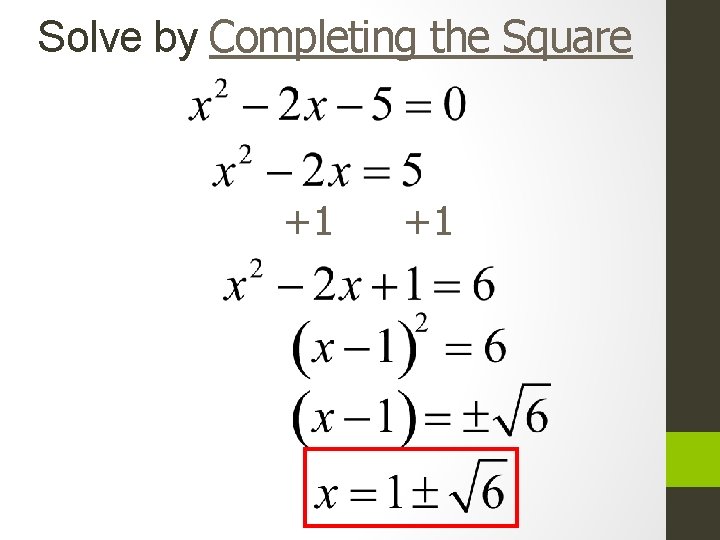
Solve by Completing the Square +1 +1

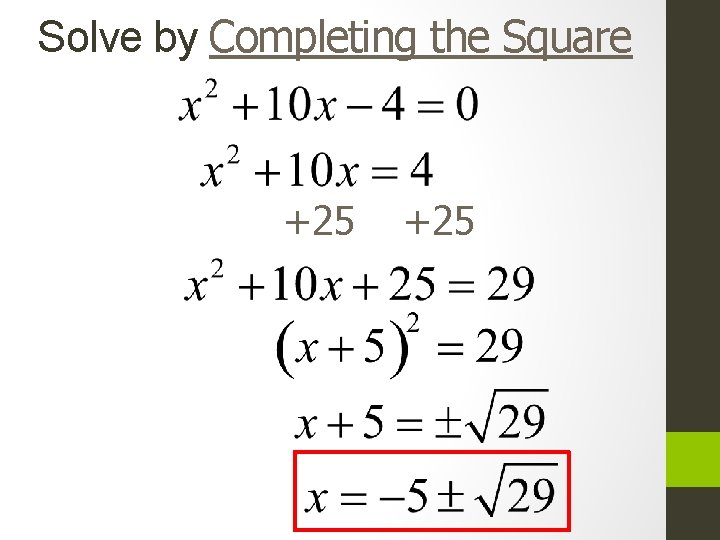
Solve by Completing the Square +25

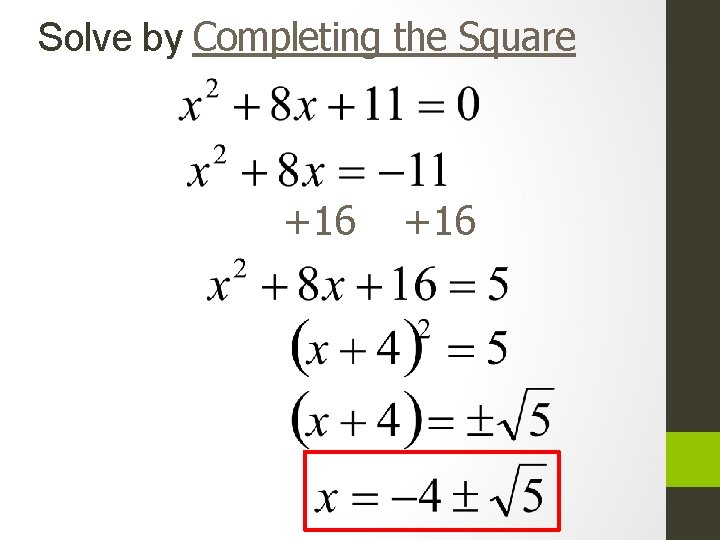
Solve by Completing the Square +16

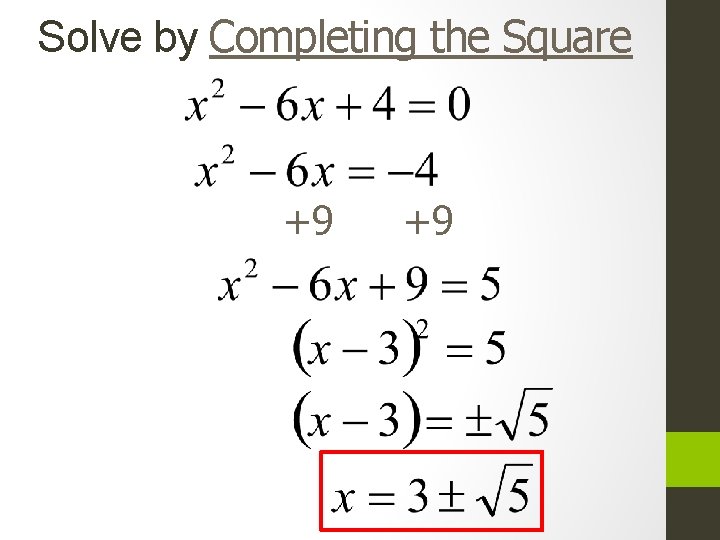
Solve by Completing the Square +9 +9

The coefficient of 2 x must be “ 1”

The coefficient of 2 x must be “ 1”