Quadratic Formula Solving Quadratics Completing the Square The

Quadratic Formula

Solving Quadratics Completing the Square

The Aim of Completing the Square … is to write a quadratic function as a perfect square. Here are some examples of perfect squares! l x 2 + 6 x + 9 l x 2 - 10 x + 25 l x 2 + 12 x + 36 Try to factor these (they’re easy).

Perfect Square Trinomials l x 2 + 6 x + 9 l x 2 - 10 x + 25 l x 2 + 12 x + 36 =(x+3)2 =(x-5)2 =(x+6)2 Can you see a numerical connection between … 6 and 9 using 3 -10 and 25 using -5 12 and 36 using 6

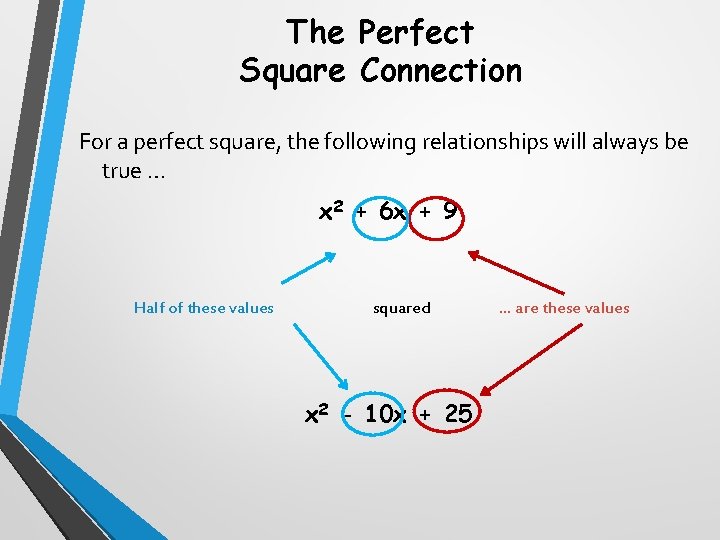
The Perfect Square Connection For a perfect square, the following relationships will always be true … x 2 + 6 x + 9 Half of these values squared x 2 - 10 x + 25 … are these values

The Perfect Square Connection l l l In the following perfect square trinomial, the constant term is missing. Can you predict what it might be? X 2 + 14 x + ____ Find the constant term by squaring half the coefficient of the linear term. (14/2)2 X 2 + 14 x + 49

Perfect Square Trinomials l Create perfect square trinomials. l x 2 + 20 x + ___ 100 l x 2 - 4 x + ___ 4 l x 2 + 5 x + ___ 25/4

q Example 2: What number should be added to Complete The Square? Square Now how do you write each as a perfect square? square a) b) c) d)

10. 5 Completing the Square Methods for Solving Quadratic Equations 1. 2. 3. 4. Factor Square Root Completing the Square Quadratic Formula

Square Root Property

Completing the Square Solve: = =

Completing the Square Solve:

Solving Quadratic Equations by Completing the Square Try the following examples. Do your work on your paper and then check your answers.

Standard 9 Write a quadratic function in vertex form Vertex form- Is a way of writing a quadratic equation that facilitates finding the vertex. y – k = a(x – h)2 ØThe h and the k represent the coordinates of the vertex in the form V(h, k). ØThe “a” if it is positive it will mean that our parabola opens upward and if negative it will open downward. ØA small value for a will mean that our parabola is wider and vice versa.

Standard to Graphing: Quadratic Find the vertex of the following equation by completing the square: y = x 2 + 8 x + 25 y = a ( x – h )2 Complete the Square: Find the “c” that completes the square GOAL + k Add to both sides y + 16 = (x 2 + 8 x + 16 ) + 25 Factor what is in the Parentheses y + 16 = (x + 4)2 + 25 y = (x + 4) 2 - 9 Vertex: Simplify (-4, 9)

Standard to Graphing: Quadratic Find the vertex of the following equation by completing the square: y = 3 x 2 – 18 x – 10 y=a ( x – h ) GOAL 2 + k y + 3 9 = 3(x 2 – 6 x + 9 ) - 10 y = 3 (x – 3)2 – 10 – 27 y = 3(x – 3)2 – 37 Vertex: (3, -37)

Standard 9 Write a quadratic function in vertex form Write y = x 2 – 10 x + 22 in vertex form. Then identify the vertex. y = x 2 – 10 x + 22 y + ? = (x 2 – 10 x + ? ) + 22 (x 2 y + 25 = – 10 x + 25) + 22 y + 25 = (x – 5)2 + 22 y = (x – 5)2 - 3 Write original function. Prepare to complete the square. ( ) 2 2 Add – 10 = (– 5) = 25 to each side. 2 Write x 2 – 10 x + 25 as a binomial squared. Write in vertex form. ANSWER The vertex form of the function is The vertex is (5, – 3). y = (x – 5)2 - 3

GUIDED PRACTICE for Examples 6 and 7 Write the quadratic function in vertex form. Then identify the vertex. 13. y = x 2 – 8 x + 17 2 ; (4, 1). y 1 = (x – 4) ANSWER 14. y = x 2 + 6 x + 3 ANSWER y + 6 = (x + 3)2 ; (– 3, – 6) 15. f(x) = x 2 – 4 x – 4 ANSWER y + 8 = (x – 2)2 ; (2 , – 8)

EXAMPLE 7 Find the maximum value of a quadratic function Baseball The height y (in feet) of a baseball t seconds after it is hit is given by this function: y = – 16 t 2 + 96 t + 3 Find the maximum height of the baseball. SOLUTION The maximum height of the baseball is the y-coordinate of the vertex of the parabola with the given equation.

EXAMPLE 7 Find the maximum value of a quadratic function y = – 16 t 2 + 96 t +3 y = – 16(t 2 – 6 t) +3 y + ? = – 16(t 2 – 6 t + ? ) + 3 y +(– 16)(9) = – 16(t 2 – 6 t + 9 ) + 3 y – 144 = – 16(t – 3)2 + 3 y = – 16(t – 3)2 + 147 Write original function. Factor – 16 from first two terms. Prepare to complete the square Add (– 16)(9) to each side. Write t 2 – 6 t + 9 as a binomial squared. Vertex Form ANSWER The vertex is (3, 147), so the maximum height of the baseball is 147 feet.

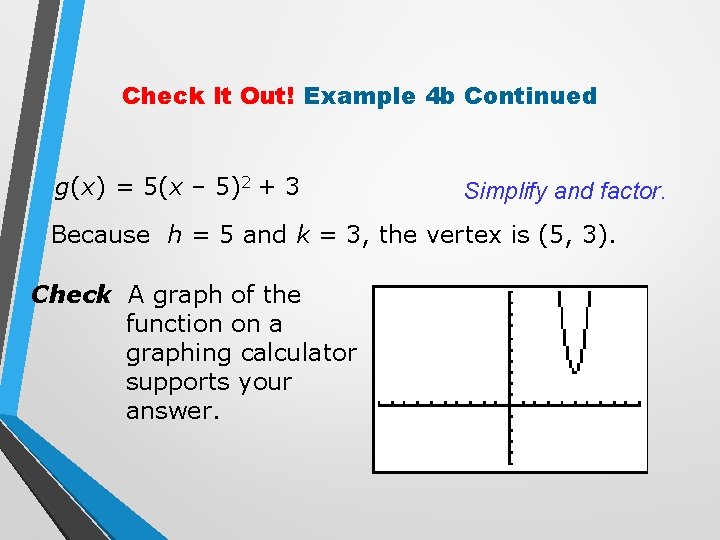
Check It Out! Example 4 b Write the function in vertex form, and identify it vertex g(x) = 5 x 2 – 50 x + 128 g(x) = 5(x 2 – 10 x) + 128 g(x)+ = 5(x 2 – 10 x + g(x)+ = 5(x 2 – 10 x + ) + 128 Factor so the coefficient of x 2 is 1. Set up to complete the square. ) + 128 Add . Because is multiplied by 5, you must add 5.

Check It Out! Example 4 b Continued g(x) = 5(x – 5)2 + 3 Simplify and factor. Because h = 5 and k = 3, the vertex is (5, 3). Check A graph of the function on a graphing calculator supports your answer.