Comparing Populations Proportions and means Comparing proportions Situation










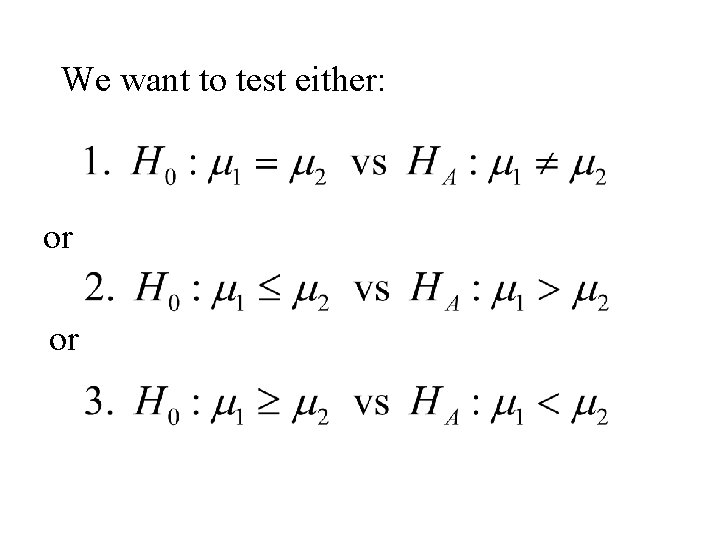


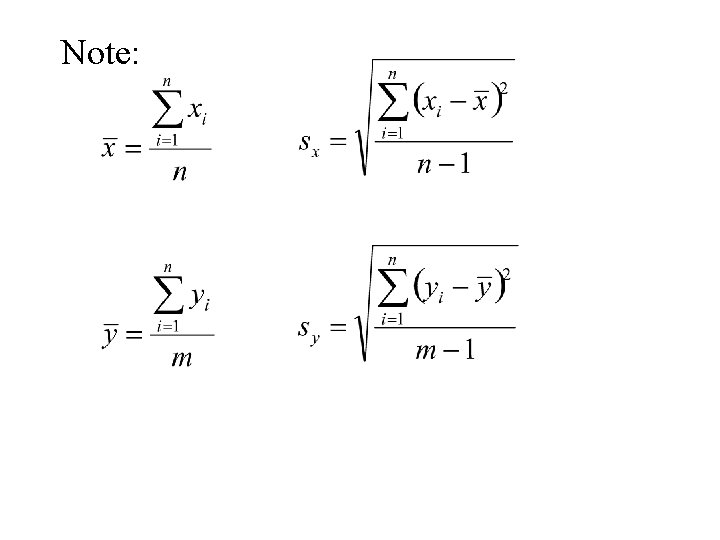


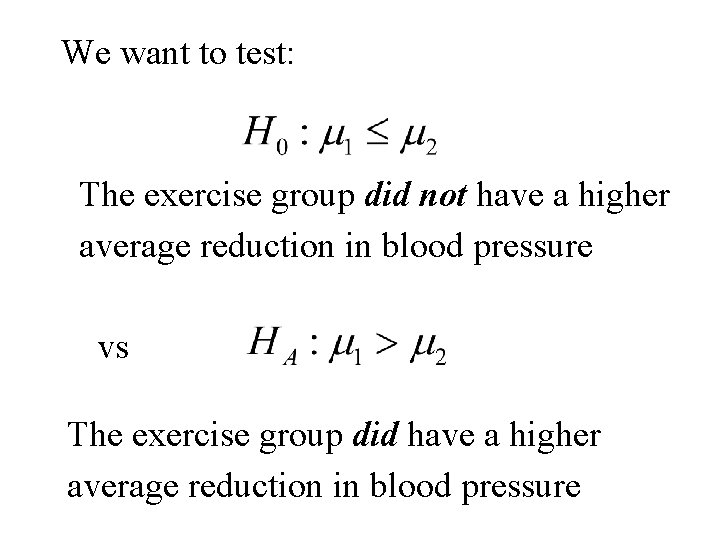











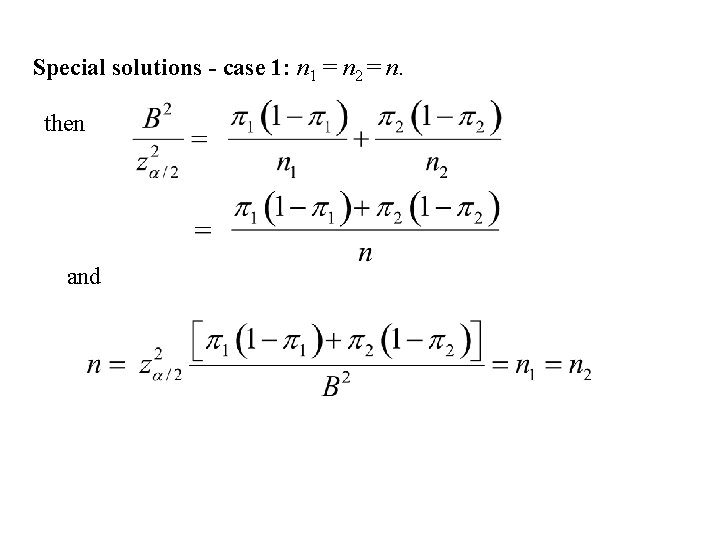

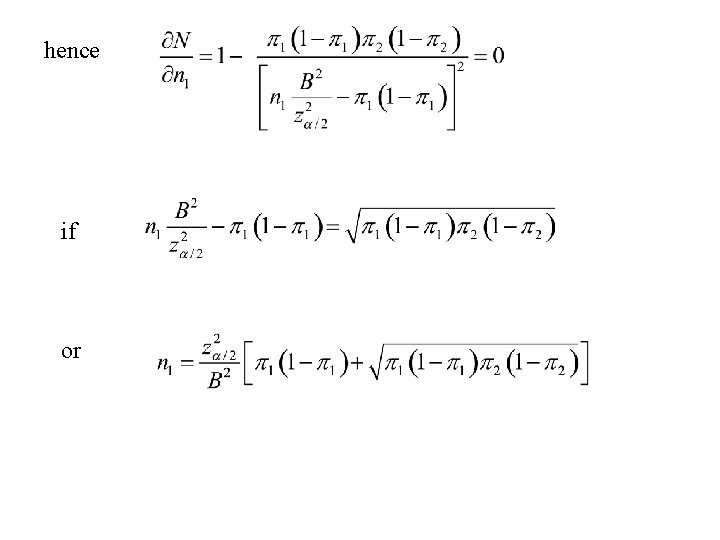
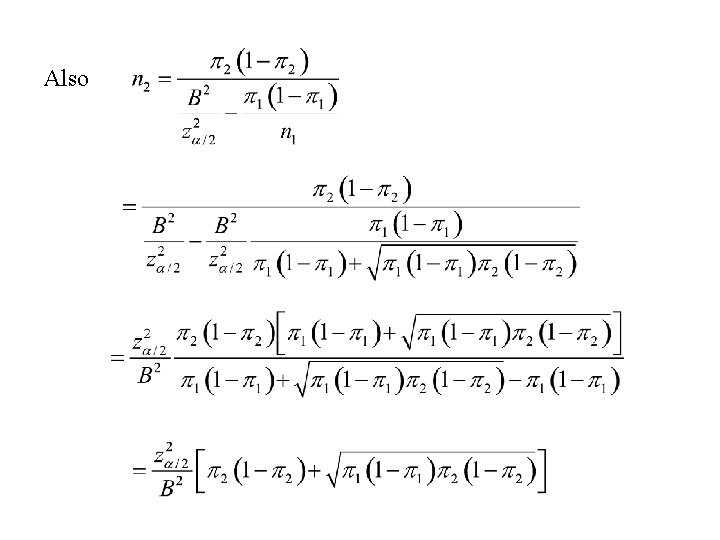


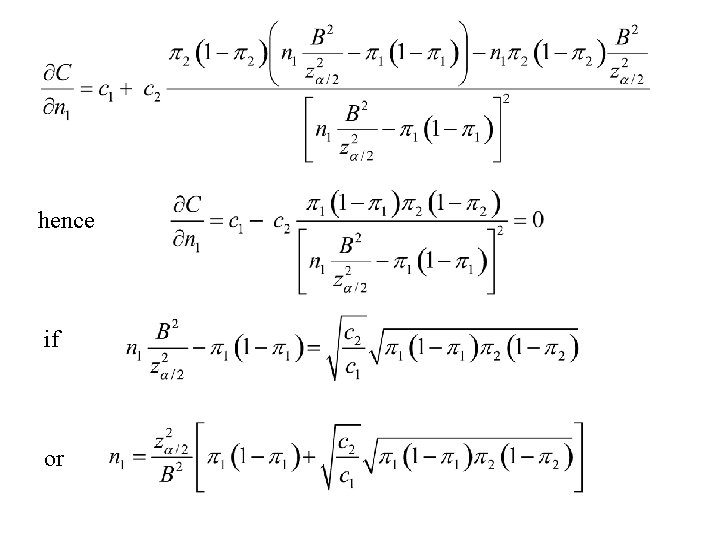
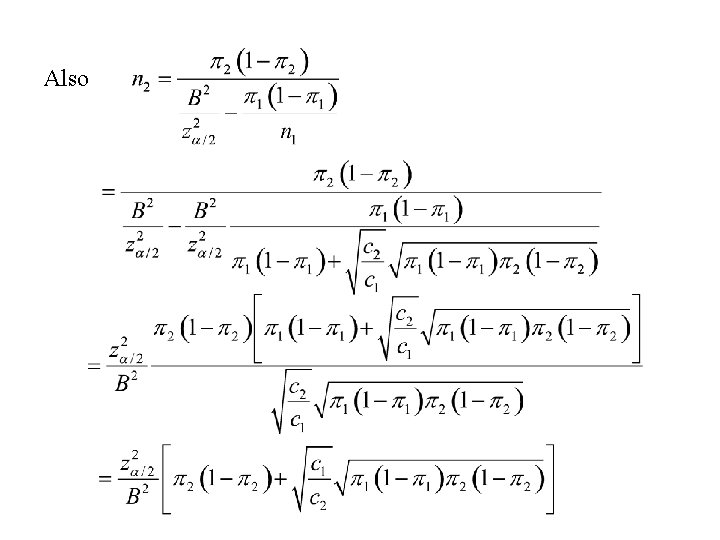



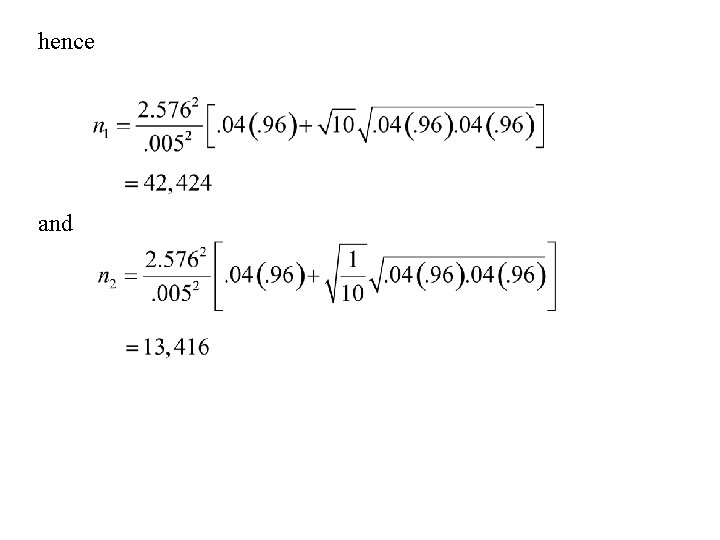




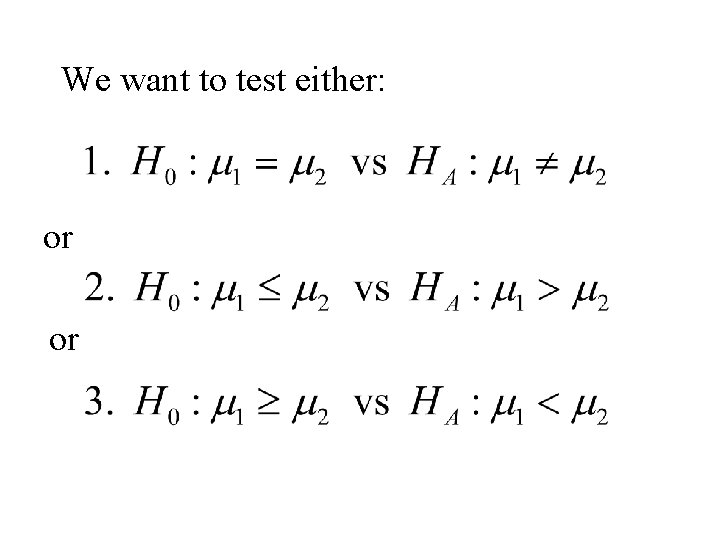



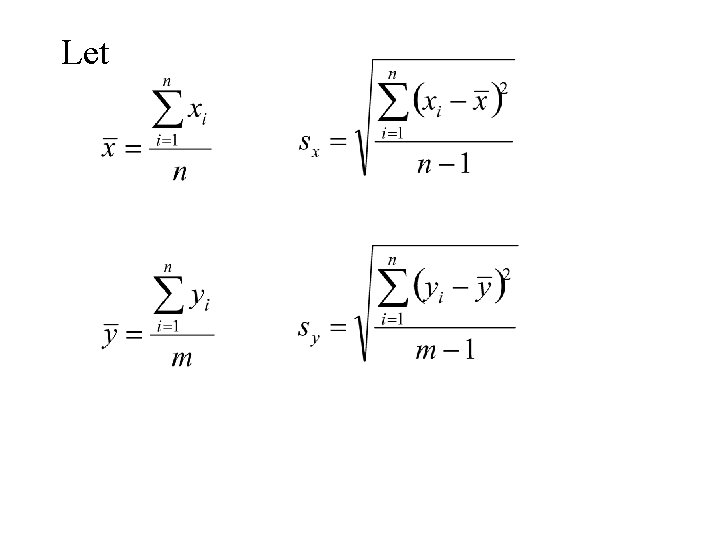




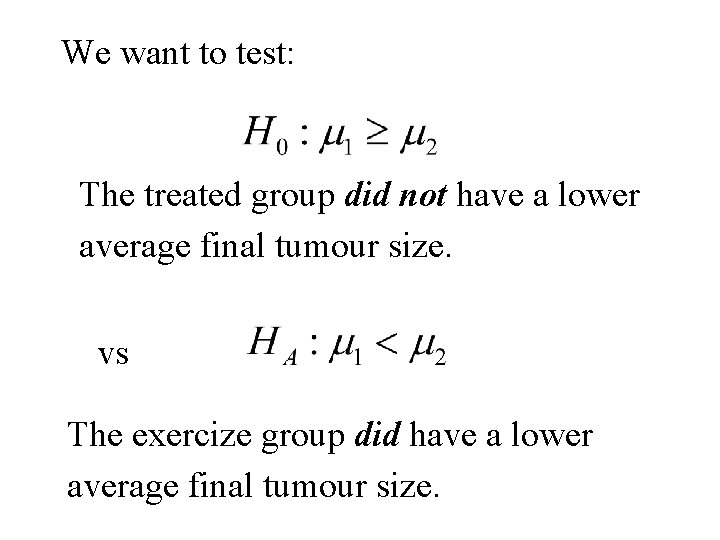



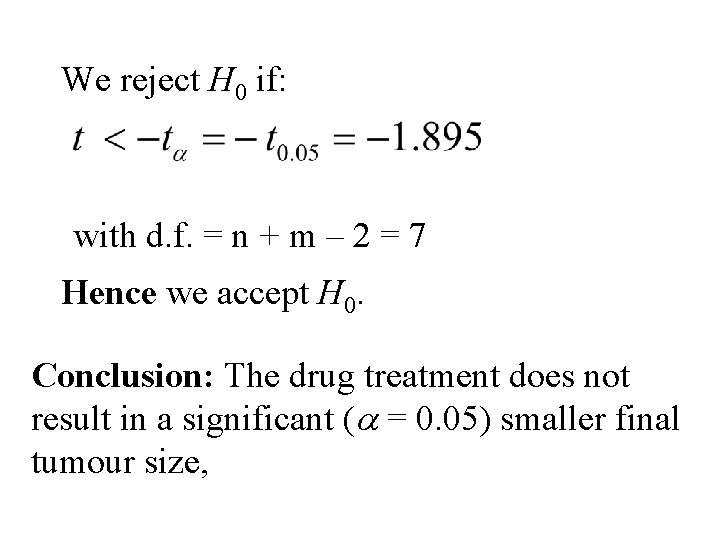
- Slides: 58

Comparing Populations Proportions and means

Comparing proportions Situation • We have two populations (1 and 2) • Let p 1 denote the probability (proportion) of “success” in population 1. • Let p 2 denote the probability (proportion) of “success” in population 2. • Objective is to compare the two population proportions

We want to test either: or or

The test statistic:

Where: A sample of n 1 is selected from population 1 resulting in x 1 successes A sample of n 2 is selected from population 2 resulting in x 2 successes

The Alternative Hypothesis HA The Critical Region

Estimating a difference proportions using confidence intervals Situation • We have two populations (1 and 2) • Let p 1 denote the probability (proportion) of “success” in population 1. • Let p 2 denote the probability (proportion) of “success” in population 2. • Objective is to estimate the difference in the two population proportions d = p 1 – p 2.

Confidence Interval for d 100 P% = 100(1 – a) % : = p 1 – p 2

Example • Estimating the increase in the mortality rate for pipe smokers higher over that for nonsmokers d = p 2 – p 1

Comparing Means Situation • We have two normal populations (1 and 2) • Let m 1 and s 1 denote the mean and standard deviation of population 1. • Let m 2 and s 2 denote the mean and standard deviation of population 1. • Let x 1, x 2, x 3 , … , xn denote a sample from a normal population 1. • Let y 1, y 2, y 3 , … , ym denote a sample from a normal population 2. • Objective is to compare the two population means
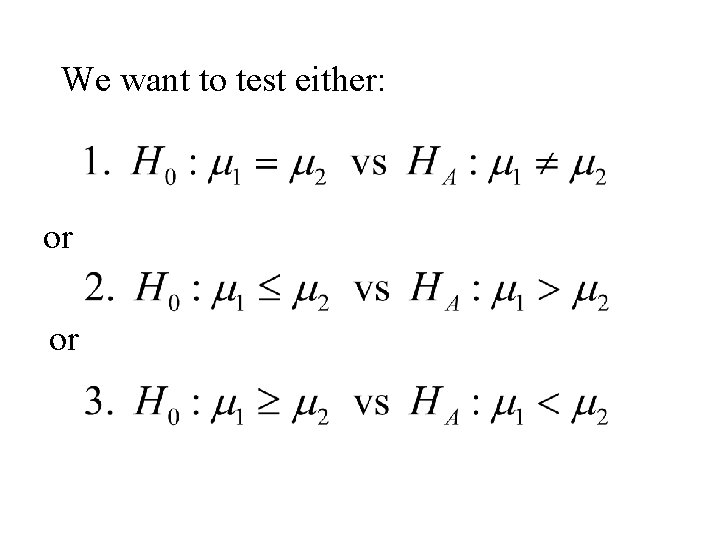
We want to test either: or or

Consider the test statistic:

If: • will have a standard Normal distribution • This will also be true for the approximation (obtained by replacing s 1 by sx and s 2 by sy) if the sample sizes n and m are large (greater than 30)
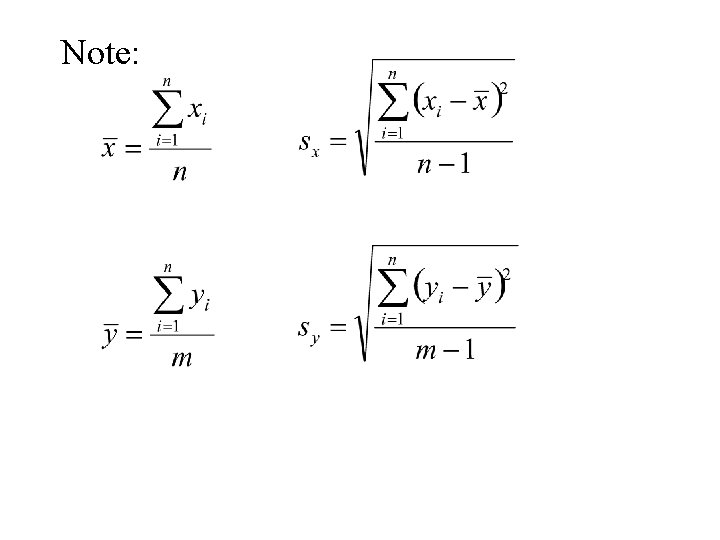
Note:

The Alternative Hypothesis HA The Critical Region

Example • A study was interested in determining if an exercise program had some effect on reduction of Blood Pressure in subjects with abnormally high blood pressure. • For this purpose a sample of n = 500 patients with abnormally high blood pressure were required to adhere to the exercise regime. • A second sample m = 400 of patients with abnormally high blood pressure were not required to adhere to the exercise regime. • After a period of one year the reduction in blood pressure was measured for each patient in the study.
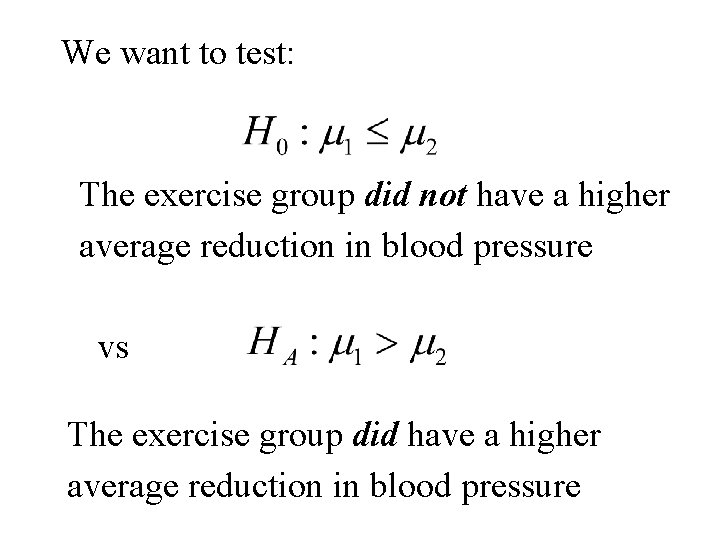
We want to test: The exercise group did not have a higher average reduction in blood pressure vs The exercise group did have a higher average reduction in blood pressure

The test statistic:

Suppose the data has been collected and:

The test statistic:

We reject H 0 if: True hence we reject H 0. Conclusion: There is a significant (a = 0. 05) effect due to the exercise regime on the reduction in Blood pressure

Estimating a difference means using confidence intervals Situation • We have two populations (1 and 2) • Let m 1 denote the mean of population 1. • Let m 2 denote the mean of population 2. • Objective is to estimate the difference in the two population proportions d = m 1 – m 2.

Confidence Interval for d 100 P% = 100(1 – a) % : = m 1 – m 2

Example • Estimating the increase in the average reduction in Blood pressure due to the exercise regime d = m 1 – m 2

Sample size determination When comparing two or more populations

Estimating a difference proportions using confidence intervals Situation • We have two populations (1 and 2) • Let p 1 denote the probability (proportion) of “success” in population 1. • Let p 2 denote the probability (proportion) of “success” in population 2. • Objective is to estimate the difference in the two population proportions d = p 1 – p 2.

Confidence Interval for d = p 1 – p 2 100 P% = 100(1 – a) % : where Note: B is determined by • The sample sizes n 1 and n 2. The level of confidence 1 – a. The probability of success in both populations, p 1 and p 2.

Note: if B, a, p 1 and p 2 are given then and Note: there are many solutions for n 1 and n 2.
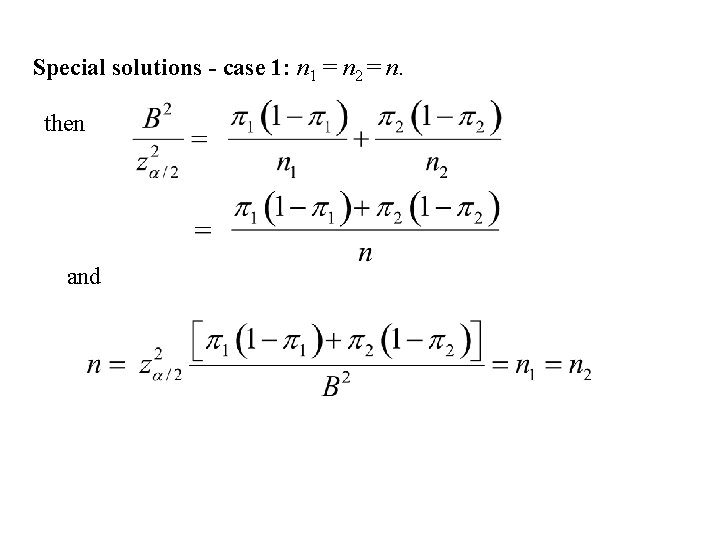
Special solutions - case 1: n 1 = n 2 = n. then and

Special solutions - case 2: Choose n 1 and n 2 to minimize N = n 1 + n 2 = total sample size Note:
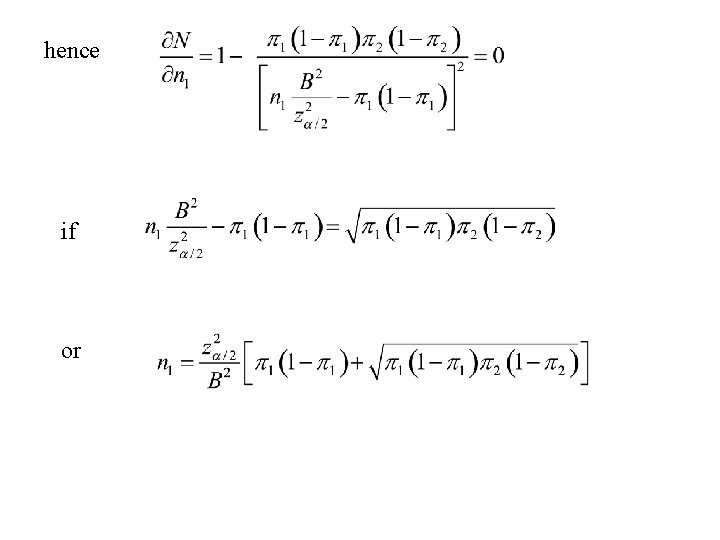
hence if or
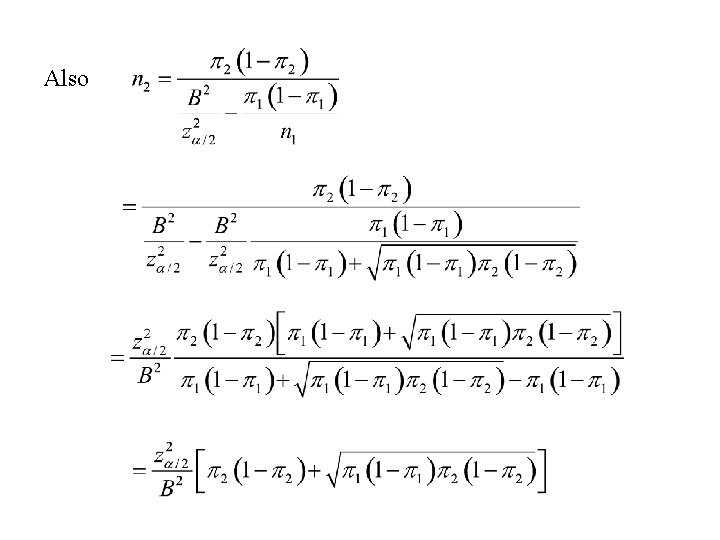
Also

Summary: The sample sizes required, n 1 and n 2, to estimate p 1 – p 2 within an error bound B with level of confidence 1 – a are: if the objectives are to minimize the total sample size N =n 1 + n 2.

Special solutions - case 3: Choose n 1 and n 2 to minimize C = C 0 + c 1 n 1 + c 2 n 2 = total cost of the study Note: C 0 = fixed (set-up) costs c 1 = cost per unit in population 1 c 2 = cost per unit in population 2
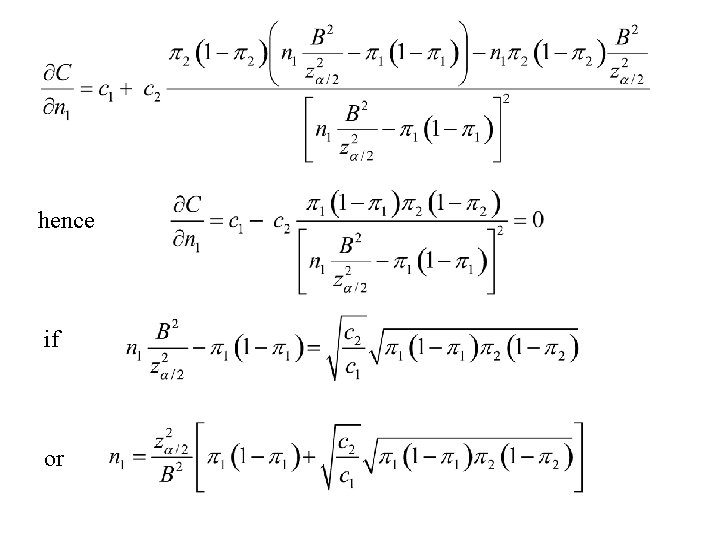
hence if or
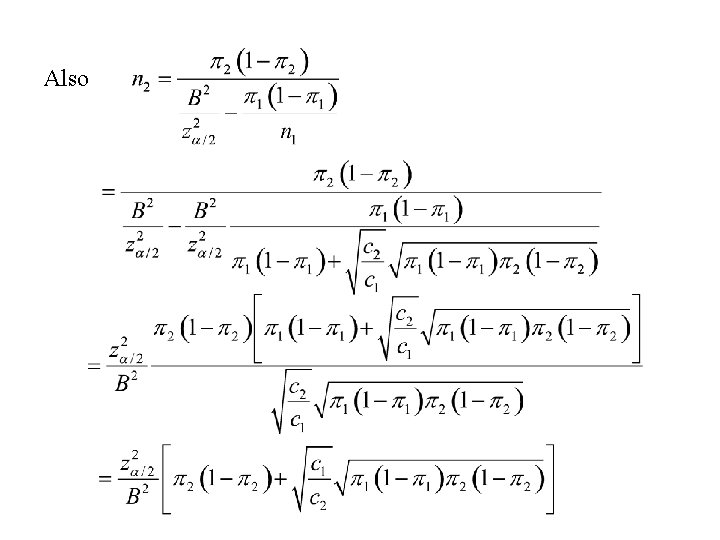
Also

Summary: The sample sizes required, n 1 and n 2, to estimate p 1 – p 2 within an error bound B with level of confidence 1 – a are: if the objectives are to minimize the total cost: C = C 0 + c 1 n 1 + c 2 n 2.

Example: It is known that approximately 4% of individuals aged 70 -80 with high cholesterol suffer a heart attack or stroke within a 10 year period. One is interested in determining if this rate is decreased for individuals who receive a new medication A study is proposed in which n 1 individuals will receive the new medication while n 2 will receive a placebo in a double blind study – both patient and physician administering the treatment are unaware of the treatment (drug or placebo) What should the sample sizes be in each group if we want to estimate the difference in the rate of heart attack or stroke within 0. 5% with a 99% level of confidence and minimize the total cost: C = C 0 + c 1 n 1 + c 2 n 2. Assume that the cost for the medication is 100 times that of the cost of administering a placebo

The sample sizes required are Where za/2 = z 0. 005 =2. 576 B = 0. 005 p 1 p 2 0. 04 and
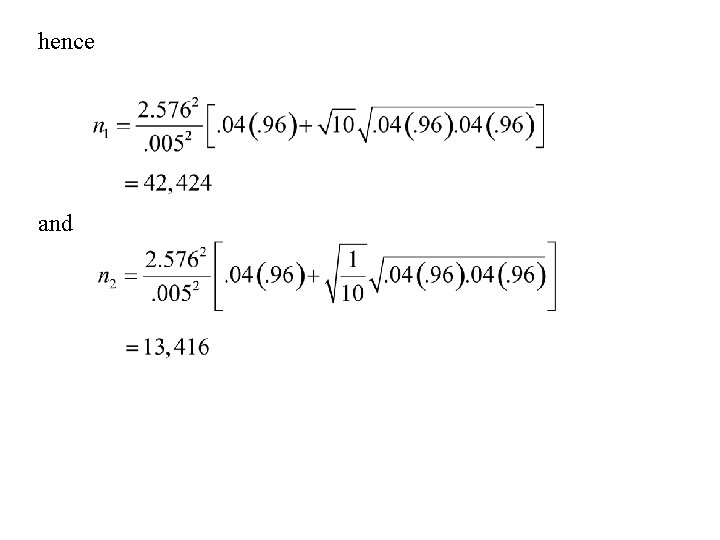
hence and

Estimating a difference means using confidence intervals Situation • We have two populations (1 and 2) • Let m 1 denote the mean of population 1. • Let m 2 denote the mean of population 2. • Objective is to estimate the difference in the two population proportions d = m 1 – m 2.

Confidence Interval for d = m 1 – m 2 100 P% = 100(1 – a) % :

The sample sizes required, n 1 and n 2, to estimate m 1 – m 2 within an error bound B with level of confidence 1 – a are: Equal sample sizes Minimizing the total sample size N = n 1 + n 2. Minimizing the total cost C = C 0 + c 1 n 1 + c 2 n 2.

Comparing Means – small samples Situation • We have two normal populations (1 and 2) • Let m 1 and s 1 denote the mean and standard deviation of population 1. • Let m 2 and s 2 denote the mean and standard deviation of population 1. • Let x 1, x 2, x 3 , … , xn denote a sample from a normal population 1. • Let y 1, y 2, y 3 , … , ym denote a sample from a normal population 2. • Objective is to compare the two population means
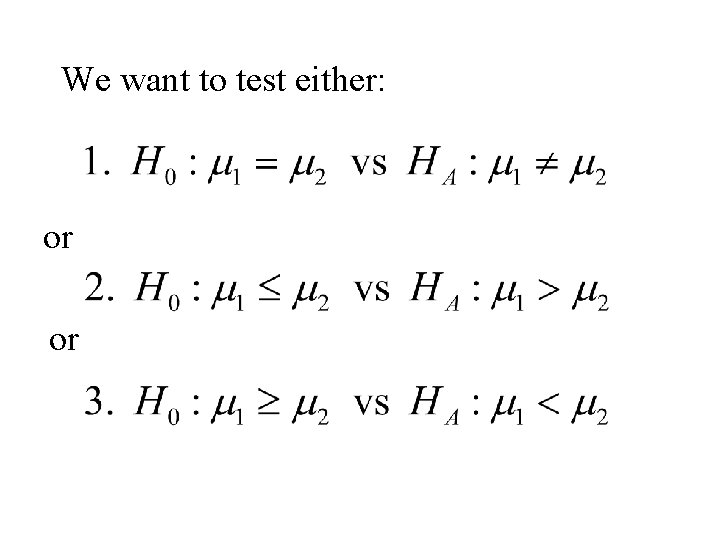
We want to test either: or or

Consider the test statistic:

If the sample sizes (m and n) are large the statistic will have approximately a standard normal distribution This will not be the case if sample sizes (m and n) are small

The t test – for comparing means – small samples Situation • We have two normal populations (1 and 2) • Let m 1 and s denote the mean and standard deviation of population 1. • Let m 2 and s denote the mean and standard deviation of population 1. • Note: we assume that the standard deviation for each population is the same. s 1 = s 2 = s
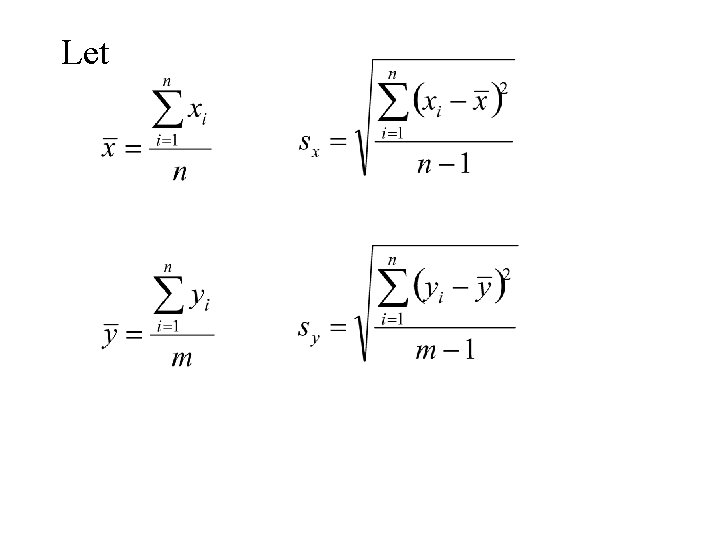
Let

The pooled estimate of s. Note: both sx and sy are estimators of s. These can be combined to form a single estimator of s, s. Pooled.

The test statistic: If m 1 = m 2 this statistic has a t distribution with n + m – 2 degrees of freedom

The Alternative Hypothesis HA The Critical Region are critical points under the t distribution with degrees of freedom n + m – 2.

Example • A study was interested in determining if administration of a drug reduces cancerous tumor size. • For this purpose n +m = 9 test animals are implanted with a cancerous tumor. • n = 3 are selected at random and administered the drug. • The remaining m = 6 are left untreated. • Final tumour sizes are measured at the end of the test period
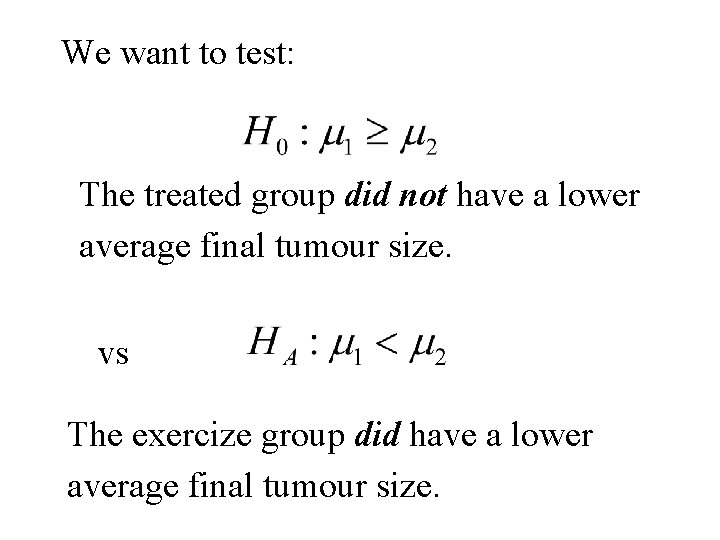
We want to test: The treated group did not have a lower average final tumour size. vs The exercize group did have a lower average final tumour size.

The test statistic:

Suppose the data has been collected and:

The test statistic:
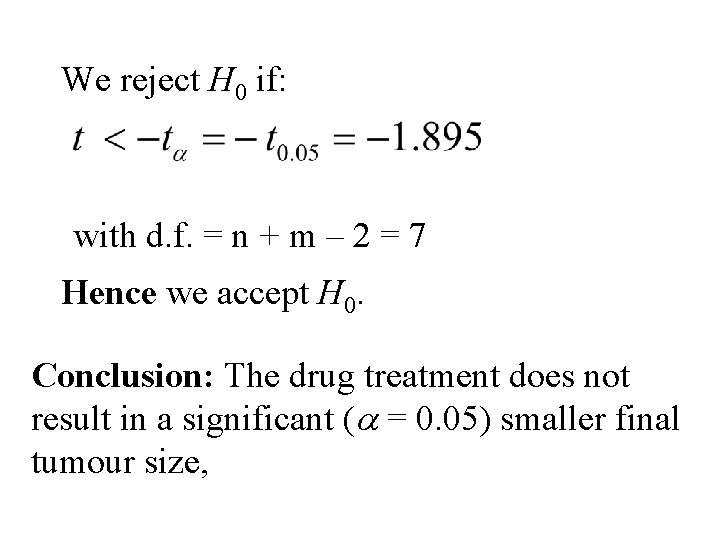
We reject H 0 if: with d. f. = n + m – 2 = 7 Hence we accept H 0. Conclusion: The drug treatment does not result in a significant (a = 0. 05) smaller final tumour size,
 Chapter 10 comparing two populations or groups answer key
Chapter 10 comparing two populations or groups answer key Chapter 10 comparing two populations or groups
Chapter 10 comparing two populations or groups Chapter 22 comparing two proportions
Chapter 22 comparing two proportions Chapter 21 comparing two proportions
Chapter 21 comparing two proportions Chapter 22 comparing two proportions
Chapter 22 comparing two proportions Chapter 22 comparing two proportions
Chapter 22 comparing two proportions Chapter 22 comparing two proportions
Chapter 22 comparing two proportions Similarity ratio definition
Similarity ratio definition Chapter 24 comparing means
Chapter 24 comparing means Comparing means in excel
Comparing means in excel Chapter 24 comparing means
Chapter 24 comparing means Poly and gon
Poly and gon Meta and morph means
Meta and morph means Define biodiversity conservation
Define biodiversity conservation Meta means and morphe means
Meta means and morphe means Stabilizing selection human birth weight
Stabilizing selection human birth weight Evolution of populations section 16-1 genes and variation
Evolution of populations section 16-1 genes and variation Why do mexico and peru have primarily catholic populations?
Why do mexico and peru have primarily catholic populations? Chapter 21 vulnerability and vulnerable populations
Chapter 21 vulnerability and vulnerable populations Bio means life logy means
Bio means life logy means Using statistical measures to compare populations
Using statistical measures to compare populations Territoires populations et développement quels défis
Territoires populations et développement quels défis A biologist discovers two populations of wolf spiders
A biologist discovers two populations of wolf spiders Limitations of punnett squares in large populations
Limitations of punnett squares in large populations Lesson 1 populations answer key
Lesson 1 populations answer key Section 19-1 review understanding populations
Section 19-1 review understanding populations Chapter 16 evolution of populations vocabulary review
Chapter 16 evolution of populations vocabulary review Gene pool
Gene pool Population definition
Population definition Section 5-1 how populations grow answer key
Section 5-1 how populations grow answer key Kar 5
Kar 5 Chapter 13 how populations evolve test
Chapter 13 how populations evolve test Chapter 17 evolution of populations answer key
Chapter 17 evolution of populations answer key 5-1 how populations grow
5-1 how populations grow Chapter 5 lesson 1 how populations grow
Chapter 5 lesson 1 how populations grow Chapter 23: the evolution of populations
Chapter 23: the evolution of populations Chapter 16 evolution of populations
Chapter 16 evolution of populations Evolution of populations section 11 review
Evolution of populations section 11 review Career development of diverse populations
Career development of diverse populations Section 5-1 how populations grow
Section 5-1 how populations grow Chapter 8 understanding populations
Chapter 8 understanding populations Complex patient populations
Complex patient populations Parasitism
Parasitism Chapter 23 the evolution of populations
Chapter 23 the evolution of populations Dynamique des populations
Dynamique des populations Chapter 13 how populations evolve
Chapter 13 how populations evolve Populations
Populations Genetic drift in small populations
Genetic drift in small populations Genetic drift in small populations
Genetic drift in small populations Genetic drift vs genetic flow
Genetic drift vs genetic flow Why are populations the smallest unit of evolution
Why are populations the smallest unit of evolution 5-1 how populations grow
5-1 how populations grow Compare and contrast hinduism and buddhism
Compare and contrast hinduism and buddhism Complete each proportion ab/bm= /cd
Complete each proportion ab/bm= /cd Ratios, rates, and proportions
Ratios, rates, and proportions 3 2 1 dough
3 2 1 dough Core focus on proportions and probability answer key
Core focus on proportions and probability answer key Law of indefinite proportion
Law of indefinite proportion Trapezoid ratio and proportion
Trapezoid ratio and proportion