Geometry 7 1 Ratio and Proportion Ratio The

Geometry 7. 1 Ratio and Proportion

Ratio The ratio of one number to another is the quotient when the first number is divided by the second. Simplest Form: ratio of 8 to 12 is If y ≠ 0, the ratio of x to y is

Ways to write a ratio 1. As a fraction b≠ 0 2. With a colon a: b 3. With words a to b With ratios, units must be the same.

Ratios are used to compare two numbers, such as side length or angle measure, but the quantities being compared must be in the same units. Example: A sheet of plywood is 0. 5 m long by 35 cm wide. Find the ratio of the length to width. Notice that the units do not affect the final ratio. The ratio is the same no matter what measuring unit you use. Also, a ratio has no units attached to it. We can use ratio to find the measure of angles.

Example: Two complementary angles have measures in the ratio 2: 7. Find the measure of each angle.

Ratios can compare more than two numbers. The notation used is a: b: c… Example: The measure of the five angles of a pentagon are in the ratio 11: 7: 5: 4: 3. Find the measure of each angle.

Proportion: an equation that states that two ratios are equal. Examples: a: b = c: d 3: 6 = 1: 2 An extended proportion is an equation relating three or more ratios. Examples: x = ______ y = ____

Express the ratio AB: AD in simplest form. Be sure that the quantities are in the same units. 1. 2. 3. 4. 5. AB 27 m 8 cm 1 m 25 cm 8 cm AD 12 m 24 cm 0. 3 m 2 m 8 m

Find the measure of each angle. 6. Two supplementary angles have measures in the ratio 3: 7. The measures of the angles of a triangle are in the ratio 2: 2: 5. Solve 8. The perimeter of a triangle is 48 cm and the lengths of the sides are in the ratio 3: 4: 5. Find the length of each side.

Homework pg. 243 CE #1 -17 Odd WE # 1 -33 odd, calc on 33

Example A rectangular playing field has a length of one kilometer and a width of 520 meters. Find the ratio of the length to the width. Length Width = 1000 ÷ 520 4 4 = 25 13 The ratio of length to width is 25 to 13, or 25: 13

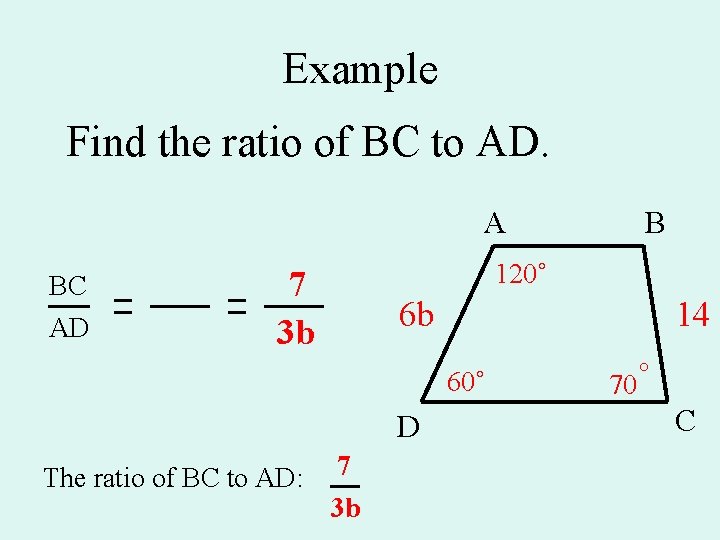
Example Find the ratio of BC to AD. A BC AD 120˚ 7 3 b 6 b 14 60˚ D The ratio of BC to AD: B 7 3 b 70˚ C

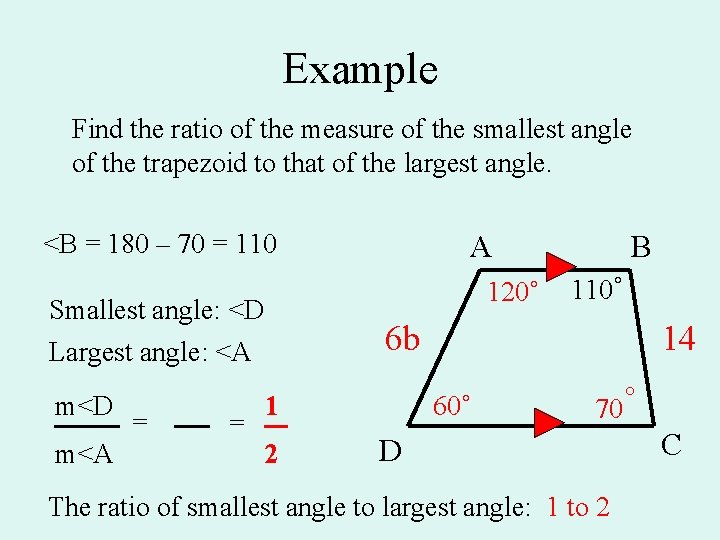
Example Find the ratio of the measure of the smallest angle of the trapezoid to that of the largest angle. <B = 180 – 70 = 110 120˚ Smallest angle: <D Largest angle: <A m<D m<A = = A B 110˚ 6 b 1 2 14 60˚ 70˚ D The ratio of smallest angle to largest angle: 1 to 2 C

Example A telephone pole 7 meters tall snaps into two parts during a wind storm. The ratio of the two parts is 3: 2. Find the length of each part. 3 x 7 2 x Let 3 x and 2 x be the two parts 3 x + 2 x = 7 5 x = 7 x= Then, 3 x = 4. 2 meters and 2 x = 2. 8 meters. These are the lengths of the two parts of the telephone pole.

Example The measures of the 5 interior angles of a pentagon are in the ratio 11: 7: 5: 4: 3. Find the measure of each angle. Let 11 x, 7 x, 5 x, 4 x and 3 x be the measures of the angles The sum of the angles is (n-2)180, or (5 -2)180. 11 x + 7 x + 5 x + 4 x + 3 x = (5 -2)180 30 x = 540 x = 18 11(18) = 198 7(18) = 126 5(18) = 90 4(18) = 72 3(18) = 54 The angle measures are 198, 126, 90, 72 and 54.

Proportion • an equation that states that two ratios are equal. • can be shown as: a b first term second term = c d or a: b = c: d third term fourth term