PROPORTION INVERSE PROPORTION INDIRECT PROPORTION Learning Objectives After

PROPORTION INVERSE PROPORTION (INDIRECT PROPORTION)

Learning Objectives: After implementing this lesson students will be able to: Comprehend inverse proportion 2. Find a value based on a inverse proportion 3. Calculating inverse proportion by cross product 4. Calculating inverse proportion by proportion 1. � The characters building: Discipline, respect, diligence and responsibility.

Description: To be easier in comprehending direct proportion, see following description! � Vina is holding a birthday party. Vina has 18 cakes that will be given to each friend equally. a. If Vina invites two friends, how many cakes will each person receive? b. If Vina invites three friends, how many cakes will each person receive? c. If Vina invites six friends, how many cakes will each person receive?

The number of cakes that will be given to each friend equally can be presented in the following table: Invited friends 2 3 4 Cakes for each 9 6 4. 5 6 12 3 1. 5 Ø The proportion of 2 friends who invited to 3 friends who invited is 2: 3 Ø The proportion of cakes for each if invited friends are 2 people to invited friends are 3 people is 9 : 6 = 3 : 2 Ø The proportion of 6 friends who invited to 12 friends who invited is 6 : 12 = 1 : 2 Ø The proportion of cakes for each if invited friends are 6 people to invited friends are 12 people is 3 : 1. 5 = 2 : 1

If we observe every two corresponding lines in the table, we will see that the proportion of the number of invited friends and the number of cakes for each is the inverse, that is: Proportion of Invited friends 2: 3 3: 4 4: 6=2: 3 6 : 12 = 1 : 2 Proportion of Cakes for each >< >< 9: 6 6 : 4. 5 : 3 3 : 1. 5 = = 3: 2 4: 3 3: 2 2: 1 The more invited friends, the lesser the number of cakes for each. Ø Proportion of invited friends and the number of cakes for each is called Inverse Proportion. §
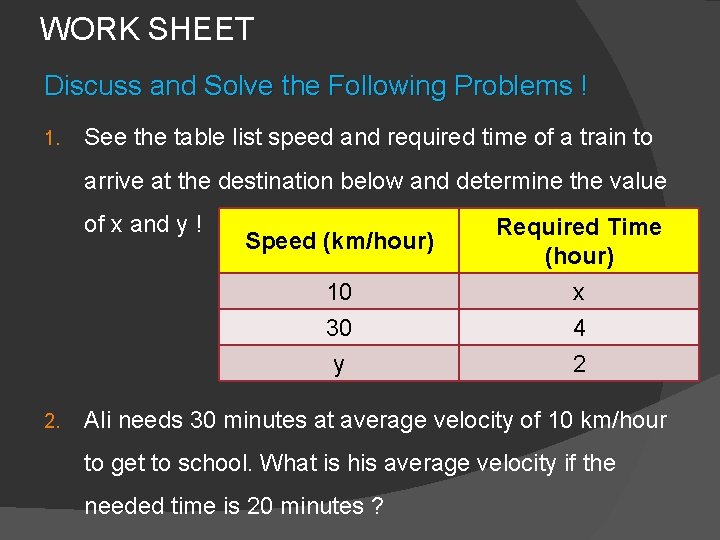
WORK SHEET Discuss and Solve the Following Problems ! 1. See the table list speed and required time of a train to arrive at the destination below and determine the value of x and y ! 2. Speed (km/hour) Required Time (hour) 10 30 y x 4 2 Ali needs 30 minutes at average velocity of 10 km/hour to get to school. What is his average velocity if the needed time is 20 minutes ?
Calculating the Inverse Proportion By Cross Product By Proportion
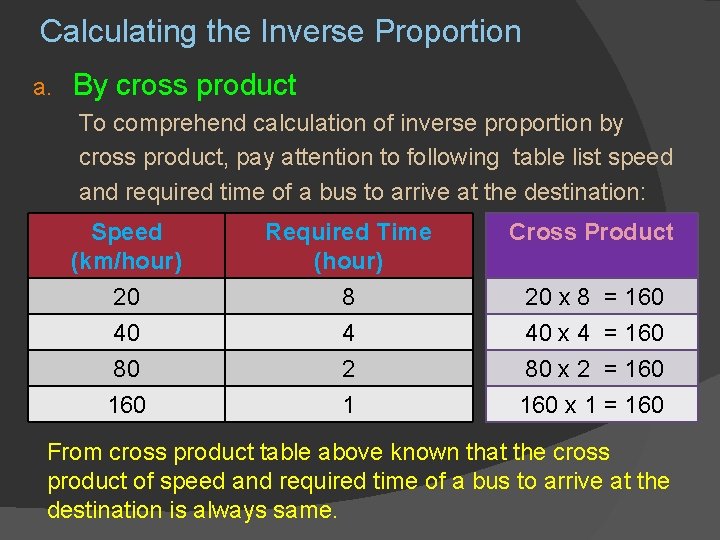
Calculating the Inverse Proportion a. By cross product To comprehend calculation of inverse proportion by cross product, pay attention to following table list speed and required time of a bus to arrive at the destination: Speed (km/hour) Required Time (hour) Cross Product 20 40 80 160 8 4 2 1 20 x 8 = 160 40 x 4 = 160 80 x 2 = 160 x 1 = 160 From cross product table above known that the cross product of speed and required time of a bus to arrive at the destination is always same.

PROBLEM EXAMPLES SOLVE BY CROSS PRODUCT THE PROBLEMS BELOW ! 1. See the table list speed and required time of a train to arrive at the destination below and determine the value of x and y ! q Speed (km/hour) Required Time (hour) 10 30 y x 4 2 Answer: We can find the value of x and y by cross product. 10 x = 30(4) 2 y = 30(4) 10 x = 120 2 y = 120 x = 12 y = 60

2. Ali needs 30 minutes at average velocity of 10 km/hour to get to school. What is his average velocity if the needed time is 20 minutes ? q Answer: We can solving this problem by cross product. Let: Ali’s average velocity if the needed time is 20 minutes to get his school = v Then, 20 v = 30(10) 20 v = 300 20 20 v = 15 Therefore, Ali’s average velocity if the needed time is 20 minutes to get his school is 15 km/hour.

Definition of Inverse Proportion The problems above are examples of inverse proportion. Proportion of invited friends and the number of cakes for each is called Inverse Proportion. Ø Proportion of speed and required time of a train to arrive at the destination is called Inverse Proportion. Ø Proportion of average velocity of Ali and the time that needed Ali to get to school is called Inverse Proportion. Ø Generally, if proportion = inverse with proportion then , with a, b, c, and d positive rational number.

Determine the whether following proportions are direct proportion or inverse proportion ! The time needed and distance travelled (Inverse Proportion) 2. Number of book and the price of book (Direct Proportion) 3. Working hours and wages (Direct Proportion) 4. Number of workers and time needed to finish a job (Inverse Proportion) 1.

Calculating the Inverse Proportion b. By Proportion To comprehend calculation of inverse proportion by Proportion, pay attention to following table the of number of invited friends to the number of cakes for each: Invited friends Cakes for each 2 (let: a) 9 (let: x) 3 (let: b) 6 (let: y) 4 (let: c) m The proportion of 2 friends who invited to 3 friends who invited is 2: 3 Ø The proportion of cakes for each if invited friends are 2 people to invited friends are 3 people is 9 : 6 = 3 : 2 Ø So that, it appears that: a y = b x so that: 3 m = 4 6

3 m = 4 6 To determine the m value we can do it like at direct proportion. That is, 3 m = 4 6 3(6) = 4 m 4 m = 3(6) 4 m = 18 4 m 18 = 4 4 m = 4. 5 Therefore, the number of cakes for each if the number of invited friends is 4. 5 cakes.

PROBLEM EXAMPLE A house can be constructed by 45 workers in 24 days. Suppose there is an order to make a house in 18 days. How many workers are needed for it ? q Answer: Let: the number of workers are needed for it = x Then, the number of workers (S 1) the number of workers (S 2) = 45 x the number of day are needed (S 1) 24 the number of day are needed (S 2) = 18 So that, 45 = 18 x 24 18 x = 24(45) 18 x = 1080 ↔ x = 60 So, the number of workers are needed in order to make a house in 18 day is 60 workers

EXERCISE A box contains candies that can be shared among 20 children and each child receives 5 candies. How many candies would each child receive if the candies are shared among 25 children ? 2. Mr. Amir needs 20 minutes at average velocity of 15 km/hour to get to the office. What is his average velocity if the needed time is 15 minutes ? 3. A video disc can rotate with velocity of 50 rotations per minute for 12 minutes. How long would the video rotate if the velocity is 40 rotations per minute ? 4. A racer can finish 1 lap in 1 minute 30 seconds with average velocity of 294 km/hour. How many laps can be done with the same amount of time if the velocity decreased to 196 km/hour ? 1.
- Slides: 16