Ratio Proportion and Percentage 1 Ratio 2 Proportion























- Slides: 27

Ratio, Proportion and Percentage 1 Ratio 2 Proportion 3 Variation 4 Percentage

Introduction The topics, ratios, proportion and percentages are concerned with dividing something into parts. A ratio shows the relative sizes of two or more values. Ratios can be shown in different ways. Using the ": " to separate. A ratio is one thing compared to or related to another thing; it is just a statement or an expression. A proportion is two ratios that have been set equal to each other; a proportion is an equation that can be solved. A percentage is a fraction whose denominator (bottom) is 100. So if we say 50%, we mean 50/100 = 1/2 (after cancelling). So 50% means ½. If want to find 10% of something, 'of' just means 'times'.

1. 1 Ratio Meaning: A ratio is a comparison of the relative values of numbers or quantities. We can write a ratio for any statement containing such a comparison. For example, that there are twice as many married employees as single employees, we mean that the ratio of married to single employees is 2: 1, where 2 represents married employees and 1 represents single employees. Definitions: a) Giri & Banerjee: “A ratio a: b is said to be the ratio of greater inequality if a > b and of lesser inequality if a < b. lf a = b, the ratio a : b is called the ratio of equality. ” b) Om P. Chug: “A ratio is a comparative relationship of two similar quantities with regards to their magnitudes and expresses what multiple or pan the first quantity is of the second. ”

1. 1 Ratio Example: The ratio of the no. of boys to the no. of girls in a school of 720 students is 3: 5. If 18 new girls are admitted in the school, find how many new boys may be admitted so that the ratio of the no. of boys to the no. of girls may change to 2: 3. Solution: The ratio of the no. of boys to the no. of girls = 3: 5 Sum of the ratios = 3 + 5 = 8 So, the no. of boys in the school = (3 x 720)/8 = 270 And the no. of girls in the school = (5 x 720)/8 = 450 Let the no. of new boys admitted be x, then the no. of boys become (270 + x). After admitting 18 new girls, the no. of girls become 450 + 18 = 468 According to given description of the problem, (270 + x)/468 = 2/3 or, 3(270+x)=2 x 468 or, 810 + 3 x = 936 or, 3 x = 126 or, x = 42. Hence the no. of new boys admitted = 42.

1. 1 Ratio A) Types of Ratio: Types of Ratio Continued Ratio Inverse Ratio

1. 1 Ratio 1) Continued Ratio: Continued Ratio is the relation (or comparison) between the magnitudes of the same kind. The continued ratio of three similar quantities a, b, c is written as a: b: Example: Suppose that Rs. 74000 are to be divided among three friends A, B, C such that A : B = 4 : 5 and B : C = 3 : 2 Sum of ratio = 12 15 10 = 37 Share of A = Share of B = Share of C =

1. 1 Ratio 2) Inverse Ratio: One ratio is inverse of another if their product is 1. Thus a: b is the inverse ratio of b/a and vice versa. Example: The monthly incomes of two persons are in the ratio 4: 5 and their monthly expenditures are in the ratio 7: 9. If each saves Rs. 50 per month, find their monthly incomes. Solution: Let the monthly incomes of two persons be Rs. 4 x and Rs. 5 x so that the ratio is Rs. 4 x: Rs. 5 x = 4: 5. If each saves Rs. 50 per month, then the expenditures of two persons are Rs. (4 x - 50) and Rs. (5 x - 50). Hence, the monthly incomes of the two persons are Rs. 4 x 100 and Rs. 5 x 100 i. e. Rs. 400 and Rs. 500.

1. 2 Proportion Meaning: An equality of two ratios is called a Proportion. Four quantities are said to be in proportion if a: b = c: d (also written as a: b : : c: d). a, b, c, d are called the terms of the proportion a) First & fourth terms are called extremes b) Second & third terms are called means (or middle terms). c) Product of extremes = Product of means. (Cross Product Rule) Definitions: a) Charles Mc. Keague: “A statement that two ratios are equal is called a proportion. If are two equal ratios, then the statement is called a proportion. ” b) Ricardo Fierro: “Let a: b and c: d represent equivalent ratios. The equation a: b = c: d is called a proportion and is read as "a is to b as c is to d"

1. 2 Proportion Properties of Proportion: 1) If a: b = c: d, then ad = bc (By cross multiplication). 2) If a : b = c : d, then b : a = d : c (Invertendo) 3) If a : b = c : d, then a : c = b : d (Alternendo) 4) If a : b = c : d, then a + b : b = c + d : d (Componendo) 5) If a : b = c : d, then a – b : b = c – d : d (Dividendo) 6) If a : b = c : d, then a + b : a – b = c + d : c – d (Componendo and Dividendo)

1. 2 Proportion A) Types of Proportion: Types of Proportion Continued Proportion Direct Proportion Inverse Proportion Compoun d Proportion

1. 2 Proportion 1) Continued Proportion: When three or more numbers are so related that the first to the second, the ratio of the second to the third, third to fourth, etc. are all equal, the numbers are said to be in continued proportion. Written as: a/b = b/c = c/d = d/e = ………………when a, b, c, d, e are in continued proportion. a) If a, b, c are in continued proportion, then middle term b is called the mean proportional between the first proportional a and third proportional c. b) If a ratio is equal to the reciprocal of the other, then either of them is in inverse (reciprocal) proportion of the other. E. g. 3/4 is in inverse proportion of 4/3 and vice versa.

1. 2 Proportion 2) Direct Proportion: If one quality is directly proportional to another it changes in the same way. As it increases, so does the others it decreases, the other decreases also. Example: If a person wants to buy one dozen pieces of soap, then he has to pay 240 Rs. If he wants to buy two dozen pieces of soap, he has to pay 480 Rs and so on. Solution: If x and y are in direct proportion, then division of x and y will be constant. In the above example, it sees that each ratio is the same. Hence, if we are dealing with quantities, which are related directly, (which are in direct proportion).

1. 2 Proportion 3) Inverse Proportion: If one quantity is inversely proportional to another, it changes in the opposite way – as it increases, the other decreases. Example: If 8 men take 4 days to build a wall, how long would it take 2 men (assuming they work at the same rate)? Solution: First, decide whether the problem is direct or inverse proportion. In this case, if less man is used, they will take longer, so it is inverse proportion. 8 men take 4 days 1 man takes 8 x 4 = 32 days 2 men take = 16 days Again we find the value of 1 by multiplying. Then divide to find the final answer.

1. 2 Proportion 4) Compound Proportion: “The proportion involving two or more quantities is called Compound Proportion” Example: 195 men working 10 hour a day can finish a job in 20 days. How many men employed to finish the job in 15 days if they work 13 hours a day: Solution: Let x be the no. of men required Days Hours Men’s 20 10 195 13 x 20 x 195 = 15 x 13 x x

1. 2 Proportion A) Types of Variation: Direct Variation Inverse variation Joint variation

1. 3 Variation 1) Direct Variation: lf two variables x and y are so related that when x increases (or decreases) in a certain ratio. y also increases (or decreases) in the same ratio. Then x is said to vary directly as y, and expressed as x α y. In such a situation we sometimes say that x varies as y or x is proportional to y. If x 1, x 2, x 3…be the values of x and y 1, y 2, y 3… Be the corresponding values of y, then x α y means, So, x α y means, And we can write x/y = k, where k is constant.

1. 3 Variation Example: a) A varies directly as b, and when b = 2, a = 7. What is the value of a when b = 10? Solution: The value of b has gone from 2 to 10. That is, it has increased five times. Therefore, the value of a will increase five times. It will go from 7 to 35. Formally, a 2 : a 1 = b 2 : b 1. a 2 : 7 = 10 : 2. 10 is five times 2. Therefore, a 2 will be five times 7. b) A varies directly as b, and when b = 8, a = 4. What is the value of a when b = 13? Solution: Proportionally, a 2 : a 1 = b 2 : b 1. That is, a 2 : 4 = 13 : 8. Alternately, 4 is half of 8. Therefore, a 2 will be half of 13, which is 6. 5.

1. 3 Variation 2) Inverse variation: If a variable x varies as the reciprocal of another variable y (i. e. , x α 1/y) then we say that x varies inversely as y. In case of inverse variation when x increases (or, decreases) in a certain ratio, y decreases (or, increases) in the same ratio. Example: Now x α 1/y, implies x = k. 1/y or, x y = k (here k is the constant of variation)

1. 3 Variation 3) Joint Variation: If a variable x varies as the product of a finite number of variables u, v, w, etc. , (i. e. , x α uvw. . . ), then x is said to vary jointly with u, v, w, etc. Here we state an important theorem, known as theorem on joint variation. If x α y, when z is constantan x α z, when y is constant. then x α y z, when both y and z vary. B) Some Important Results: a) If x α y then y α x. b) If x α y and y α z, then x α z. c) If x α y, then x n α y n, where n is a constant d) lf x α z and y α z, then x+y α z, x - y α z and x y α z 2 e) If x α y and w α z, then x w α y z and x/w α y/z.

1. 4 Percentage is a mathematical concept that appears very frequently in everyday life. You read that a merchant is offering a twenty percent discount on a selected group of items. The manufacturer of an article of clothing states that the material is sixty-five percent Dacron and thirty five percent polyester. A) The Meaning of Percent: Percent is a term derived from two Latin words per centum which mean by the hundred. The symbol for percent is i. e. observing this symbol carefully, one notices that it contains the numerals which represent the number one hundred. Percent means hundredths. One hundredths equal one whole item. If a percent is less than 100% it is equivalent to a fraction less than one. If a percent is more than 100% it is equivalent to a fraction greater than one.

1. 4 Percentage B) Computing Percentages: To compute a percentage of a specific number. follow the steps below: a) Change the percent to the decimal form. b) Multiply the decimal form times the specific number. c) Count all places to the right of the decimal points in the problem. d) Place the decimal the same number of places to the right of the decimal in the answer. Case 1) : Percentages less than 100: Example: 30% of 80 = 80 X. 30 = 24. 00 Answer: 30% of 80 = 24 Case 2) : Percentages greater than 100: Example: 200% of 75 = 75 X 2. 00 = 150 Answer: 200% of 75 = 150.

1. 4 Percentage C) Some Formulas in Percentage: 1) Percentage Change: % change = new value - original value × 100 Original value 2) Percentage Error % error = Error × 100 Real value 3) Percentage Increases and Interest New value = 100 + percentage increase × original value 100 4) Compound Interest: (100 + %change)no of years × original value 5) Percentage decreases New value = 100 - percentage decrease × original value 100

1. 4 Percentage D) Computing percentage of following: 1) Sales tax and Gratuities: Sales tax is levied on the sale of a commodity, which is produced or imported and sold for the first time. If the product is sold subsequently without being processed further, it is exempt from sales tax. Example: Mary bought a purse for Rs. 100 and a pair of shoes for Rs. 190. What total amount did she pay if a 7. 5% sales tax was added to the price of the items? Solution: Rs. l 00 + Rs. 190 = Rs. 290 7. 5/100 x 290/1= Rs. 21. 75 Sales Tax Rs. 290 + Rs. 21. 75 = Rs. 311. 75 Total Paid So, Mary has to paid 311. 75 Rs. Totally.

1. 4 Percentage 2) Discount: A good way to save money is to shop when merchandise is on sale. After Christmas many stores reduce the prices of toys, furniture, and other household items. In late February and March winter clothing usually is cleared out at lowered prices. Following the fourth of July there are reductions on summer items. Example: Janet bought a coat which usually sells for Rs. 980. 00 at 25% off. What did she pay for the coat? Solution: 25/100 x Rs. 980. 00 = 1/4 x 980. 00 = Rs. 245. 0 Rs. 980. 00 -Rs. 245 =Rs. 735. 0 So, Janet paid Rs. 735. 0 for the coat.

1. 4 Percentage 3) Commission: Manufacturers and producers of goods are not always able to sell their own products. It is necessary for them to employ agents to sell the articles for them. The pay received by the agent, or salesman, for work or services performed is called commission. Sometimes the commission is a certain amount for each article sold. Other times it is a percentage of the dollar value of the sales. Example: A salesman who works on a commission basis receives 12% of his sales. How much was his commission on a sale amounting to Rs. 2650? Solution: Let N= the missing number. Change 12% to 12/100 x 2650/1= N 31800/100= N N = Rs. 318. 0 The salesman earned Rs. 318. 0 commission.

1. 4 Percentage 4) Simple interest: Just as people pay for the use of items belonging to others, they pay for the use of money belonging to someone else. The price paid for the use of money is called interest. Simple interest is the amount paid on a sum of money, borrowed or invested, which remains unchanged for a specific period of time. Example: Steve borrowed Rs. 120000 at 14% per year simple interest for 8 months. What was the total amount due when he repaid the loan? Solution: Principal = Rs. 120000 Rate of Interest = 14/100 Time = 8/12 year Interest = Principal x Rate x Time Interest = Rs. 120000/1 x 14/100 x 8/12 = Rs. 11200. 00 Amount Due = Principal + Interest Amount Due = Rs. 120000 + Rs. 11200. 0 = Rs. 131200. 0

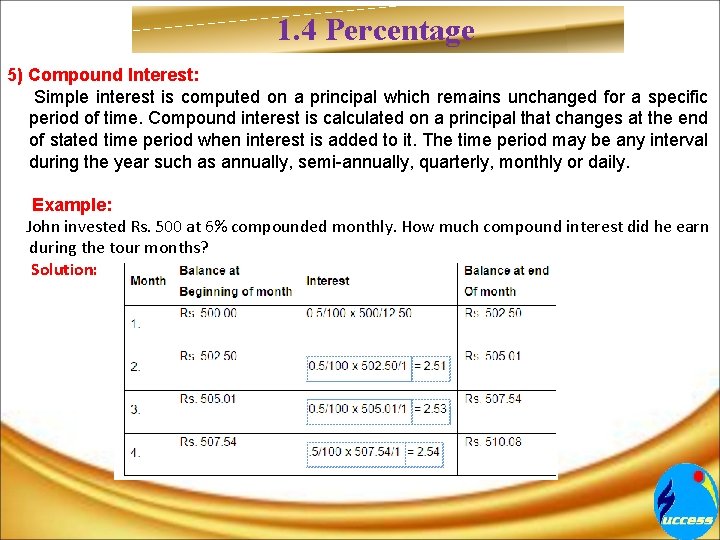
1. 4 Percentage 5) Compound Interest: Simple interest is computed on a principal which remains unchanged for a specific period of time. Compound interest is calculated on a principal that changes at the end of stated time period when interest is added to it. The time period may be any interval during the year such as annually, semi-annually, quarterly, monthly or daily. Example: John invested Rs. 500 at 6% compounded monthly. How much compound interest did he earn during the tour months? Solution: