Ratio Rates Proportions Ratios A ratio is a




































- Slides: 47

Ratio, Rates, & Proportions

Ratios • A ratio is a comparison of two numbers. o Example: Tamara has 2 dogs and 8 fish. The ratio of dogs to fish can be written in three different ways. *** Be careful with the fraction ratios – they don’t always have identical meanings to other fractions***

• There are two different types of ratios o. Part-to-Part Ratios § Example: Tamara’s dogs to cats is 2 to 8 or 1 to 4 o. Part –to-Whole Ratios § Example: Tamara’s dogs to total pets is 2 to 10 or 1 to 5

Try the following Apples to bananas Oranges to apples • There are 12 apples and 3 bananas • There are 15 oranges and 12 apples • So the ratio of apples to bananas is • So the ratio of oranges to apples is 4: 1, 4 to 1, OR 5: 4, 5 to 4, OR

A large bouquet of flowers is made up of 18 roses, 16 daisies, and 24 irises. Write each ratio in all three forms in simplest form. Identify which ratios are part-to-part and which ratios are part-to-whole. 1. Roses to iris 2. Iris to daisies 18 to 24 24 to 16 3 to 4 3 to 2 3. Daisies to roses 16 to 18 8 to 9 4. all flowers to roses 58 to 8 29 to 9

9 Explain why the ratio is not written as a mixed number: • The ratio is comparing two number. If you changed it to a mixed number it would no longer be a comparison. This is why fraction ratios are tricky

Comparing Ratios • Compare ratios by writing in simplest form o Are these ratios equivalent? 250 Kit Kats to 4 M&M’s and 500 Kit Kats to 8 M&M’s = o 12 out of 20 doctors agree and 12 out of 30 doctors agree ≠ o The ratio of students in Ms. B’s classes that had HW was 8 to 2 and 80% of Mrs. Long’s class had HW =

Rates • A rate is a ratio that compares two different quantities or measurements. • Rates can be simplified • Rates use the words per and for o Example: Driving 55 miles per hour o Example: 3 tickets for $1

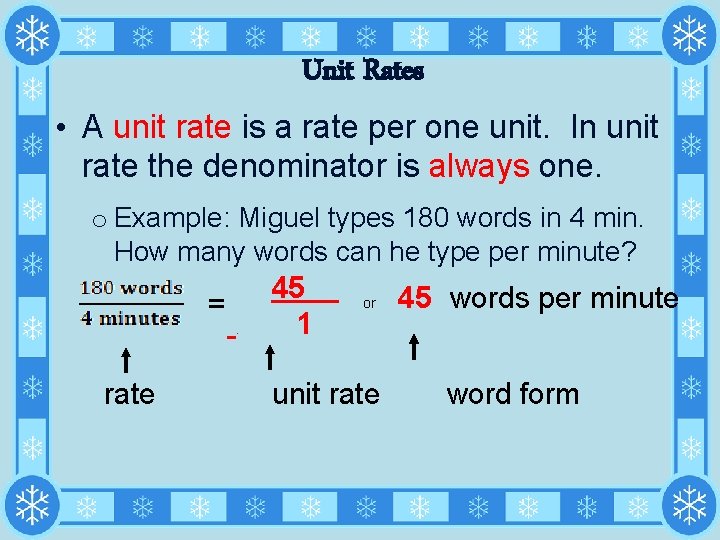
Unit Rates • A unit rate is a rate per one unit. In unit rate the denominator is always one. o Example: Miguel types 180 words in 4 min. How many words can he type per minute? =. 45 1 or 45 words per minute rate unit rate word form

• Unit rates make it easier to make comparisons. o Example: Taylor can type 215 words in 5 min § How many words can he type per minute? § Who is the faster typist? How much faster? Taylor is 2 wpm faster than Miguel

Try the Following 1. Film costs $7. 50 for 3 2. Drive 288 miles on 16 gallons of gas. rolls $2. 50 per roll 18 mpg 4. Earn $49 for 40 hours of 3. 90 students and 5 18 students per teacher work teachers $1. 23 per hour 5. **Snowfall of 12 ¾ 2 5/6 per hour inches in 4 ½ hours. 6. Use 5 ½ quarts of water for every 2 lbs of 2 ¾ quarts per lb chicken 7. Ian drove 30 miles in 60 mph 0. 5 hours 15 mph 8. Sarah drove 5 miles in 20 minutes

Complex Unit Rates • Suppose a boat travels 30 miles in 2 hours o How do you write this rate? • Suppose a boat travels 12 miles in 2/3 hours o How do you write this as a rate? o How do you write this as a division problem? o Determine the unit rate: 18 mph

• Suppose a boat travels 8 ¾ miles in 5/8 hours. o How do you write this as a rate? o How do you write this as a division problem? o Determine the unit rate: 14 mph

• . Complex fractions are fractions that have fractions within them. They are either in the numerator, denominator, or both. • Divide complex fractions by multiplying (keep, change)

TRY the FOLLOWING Write each rate. Then determine the unit rate and write in both fraction and word form 1. Mary is making pillows for her Life Skills class. She bought yards of fabric. Her total cost was $16. What was the cost per yard? $5. 82 per yard 3. Doug entered a canoe race. He rowed miles in hour. What is his average speed? 7 mph 3. Mrs. Robare is making costumes for the school play. Each costume requires 0. 75 yards of fabric. She bought 6 yards of fabric. How many costumes can Mrs. Robare make? 4. 8 costumes A lawn company advertises that they can spread 7, 500 square feet of grass seed in hours. Find the number of square feet of grass seed that can be spread in an hour. 3000 ft per hour

Comparing Unit Rates Dario has two options for buying boxes of pasta. At Corner. Market he can buy seven boxes of pasta for $6. At Super. Foodz he can buy six boxes of pasta for $5. • He divided 7 by 6 and got 1. 166666667 at Corner. Market. He then divided 6 by 7 and got 0. 85714286. He was confused. What do these numbers tell him about the price of boxes of pasta at Corner. Market? 1. 166667 is the number of boxes you can get for $1 0. 85714286 is the price per box • Decide which makes more sense to you Price per box • Compare the two stores’ prices. Which store offers the better deal? CM - $0. 86 per box SF - $0. 83 per box

Proportions

• Two quantities are proportional if they have a constant ratio or unit rate. • You can determine proportionality by comparing ratios o Andrew earns $18 per hour for mowing lawns. Is the amount he earns proportional to the number of hours he spends mowing? Earnings ($) 18 36 54 72 • Make a table to show these amounts Time (h) 1 2 3 4 • For each number of hours worked, write the relationship of the amount he earned and hour as a ratio in simplest Since each rate simplifies to 18, they are all equivalent. form. This means the amount of money Andrew earns is proportional to the number of hours he spends mowing. • Are all the rates equivalent?

o Uptown Tickets charges $7 per baseball game ticket plus $2 processing fee per order. Is the cost of an order proportional to the number of tickets ordered? • Make a table to show these amounts Cost ($) Tickets Ordered 10 1 17 2 24 3 31 4 • For each number of tickets, write the relationship of the cost of the and the number of tickets ordered. • Are all the rates equivalent? The rates are not equivalent. This means the total cost of the tickets is not proportional to the number of tickets sold.

o Use the recipe to make fruit punch. Is the amount of sugar used proportional to the amount of mix used? Explain. Cups of Sugar ½ 1 1 ½ 2 Envelopes of Mix 1 2 3 4 • Yes, they all reduce to ½ o In July, a paleontologist found 368 fossils at a dig. In August, she found about 14 fossils per day. • Is the number of fossils the paleontologist found in August proportional to the number of days she spent looking for fossils that month? No, July average 11. 87 fossils per day

Solving Proportions

• A proportion is two equivalent ratios • When solving proportions we must first ask ourselves – “What are we comparing A lemonade recipe calls for ½ cup of mix for every quart of water. If Jeff wanted to make a gallon of lemonade, is 2 cups of mix proportional for this recipe? YES Determine if the following ratios are proportional? No, 340 ≠ 270 Yes, 72 = 72

b. • Proportionality can also be determined between c. two ratios by simplifying or comparing their cross products • If they reduce to the same ratio, or their cross products are the same, then they are proportional • You can also solve proportions for a missing variable by cross multiplying. o Example: Determine if the two ratios are proportional: Yes 72 = 72 No 32 = 30 No 30 = 70

o Example: Determine the value of x: x = 60 o Example: A stack of 2, 450 one-dollar bills weighs five pounds. How much do 1, 470 one-dollar bills weigh? § Set up a proportion – ask ourselves “what are we comparing? ” 3 pounds o Example: Whitney earns $206. 25 for 25 hours of work. At this rate, how much will Whitney earn for 30 hours of work? $247. 50 $8. 25 per hour § How much does Whitney earn per hour?

Coordinate Plane Review

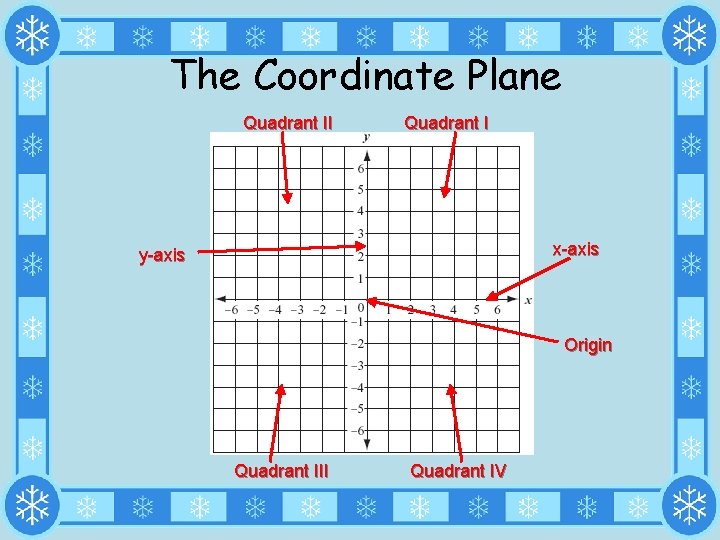
The Coordinate Plane Quadrant II Quadrant I x-axis y-axis Origin Quadrant III Quadrant IV

• Ordered Pair: is a pair of numbers that can be used to locate a point on a coordinate plane • Graph the • You can also solve proportions for a missing variable by cross multiplying. o Example: Determine if the two ratios are proportional: Yes 72 = 72 No 32 = 30 No 30 = 70

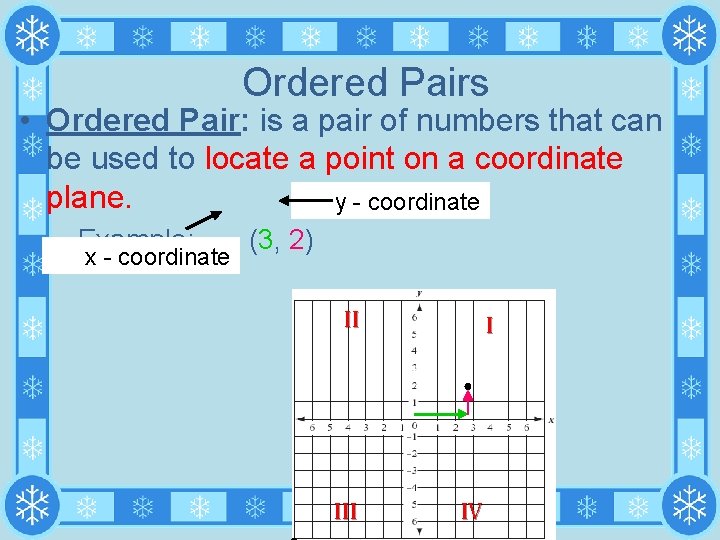
Ordered Pairs • Ordered Pair: is a pair of numbers that can be used to locate a point on a coordinate plane. y - coordinate – Example: (3, 2) x - coordinate II I ● III IV

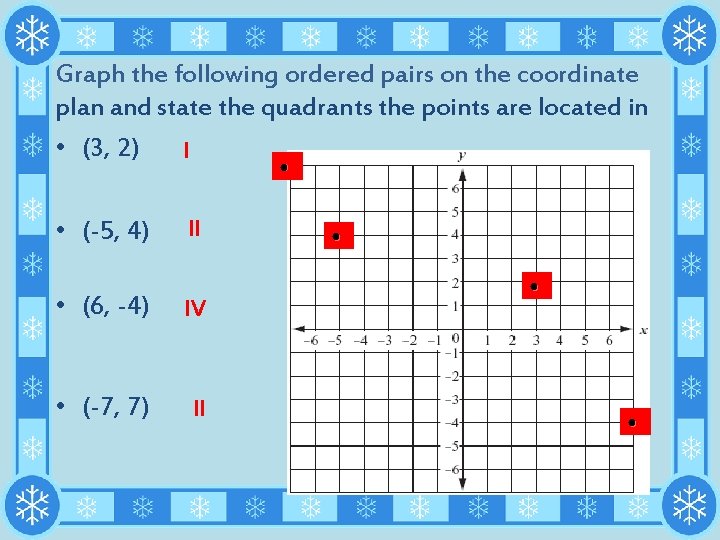
Graph the following ordered pairs on the coordinate plan and state the quadrants the points are located in • (3, 2) I ● • (-5, 4) II ● ● • (6, -4) IV • (-7, 7) II ●

Steps for Graphing

1. Draw and label the x and y axis – don’t forget your arrows 2. Make a table of values to represent the problem. Be sure to include the values: -1, 0, 1, and 2 3. Graph your order pairs- you need at least 3 points to make a line 4. Draw a line through the points – don’t forget your arrows 5. If the line is straight and goes through the origin, then the quantities are proportional

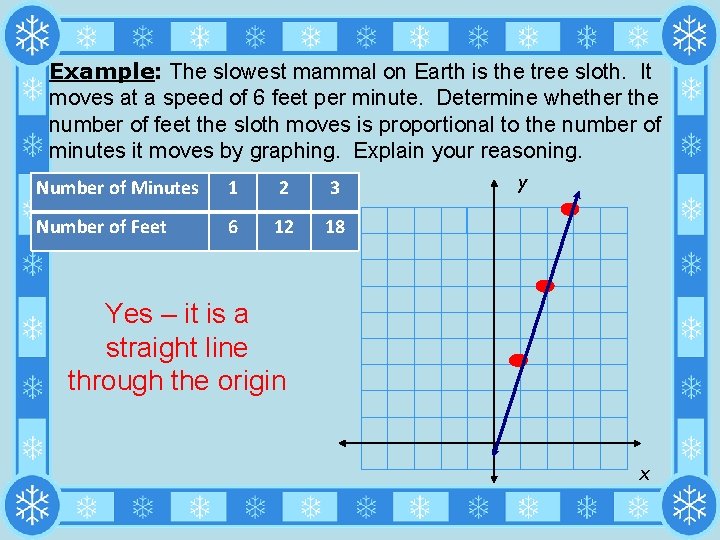
Example: The slowest mammal on Earth is the tree sloth. It moves at a speed of 6 feet per minute. Determine whether the number of feet the sloth moves is proportional to the number of minutes it moves by graphing. Explain your reasoning. Number of Minutes 1 2 3 Number of Feet 6 12 18 y Yes – it is a straight line through the origin x

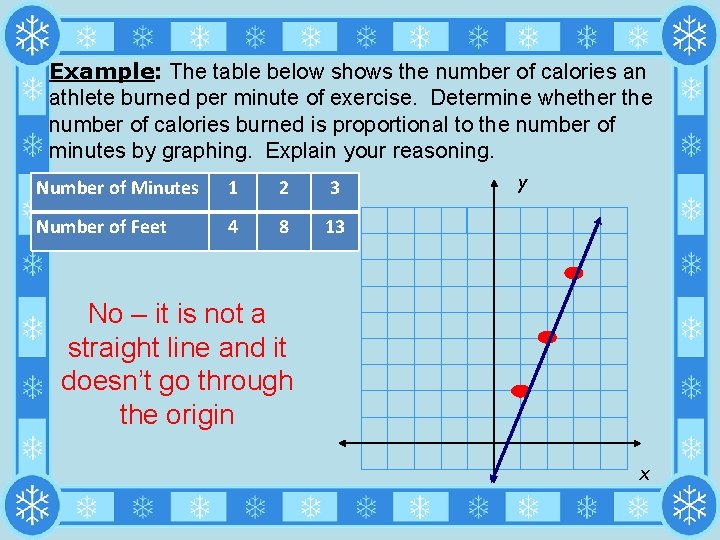
Example: The table below shows the number of calories an athlete burned per minute of exercise. Determine whether the number of calories burned is proportional to the number of minutes by graphing. Explain your reasoning. Number of Minutes 1 2 3 Number of Feet 4 8 13 y No – it is not a straight line and it doesn’t go through the origin x

Slope

• . Slope is the rate of change between any two points on a line • The sign of the slope tells you whether the line is positive or negative. • You can find slope of a line by comparing any two points on that line • Slope is the or

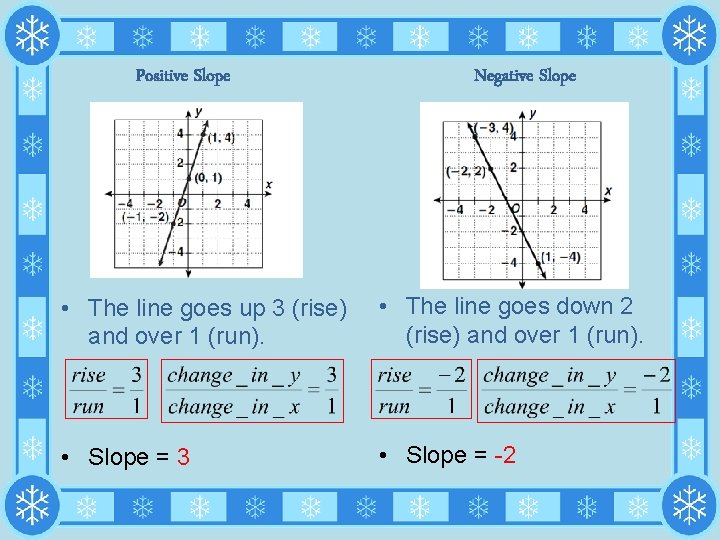
Positive Slope Negative Slope • The line goes up 3 (rise) and over 1 (run). • The line goes down 2 (rise) and over 1 (run). • Slope = 3 • Slope = -2

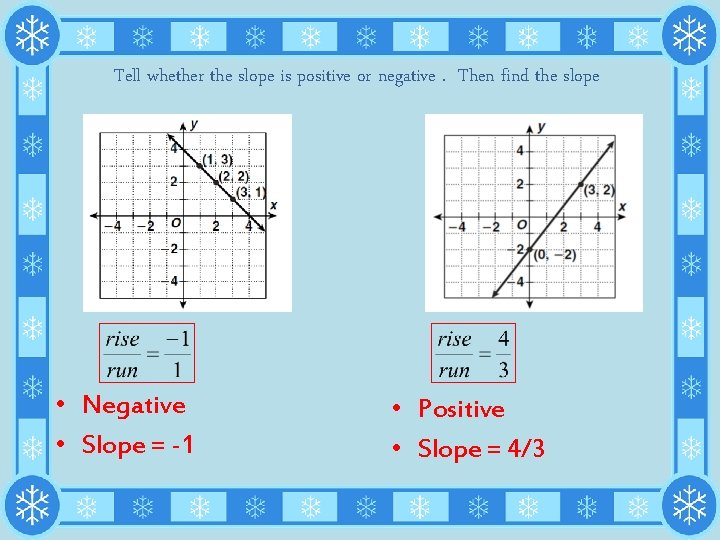
Tell whether the slope is positive or negative. Then find the slope • Negative • Slope = -1 • Positive • Slope = 4/3

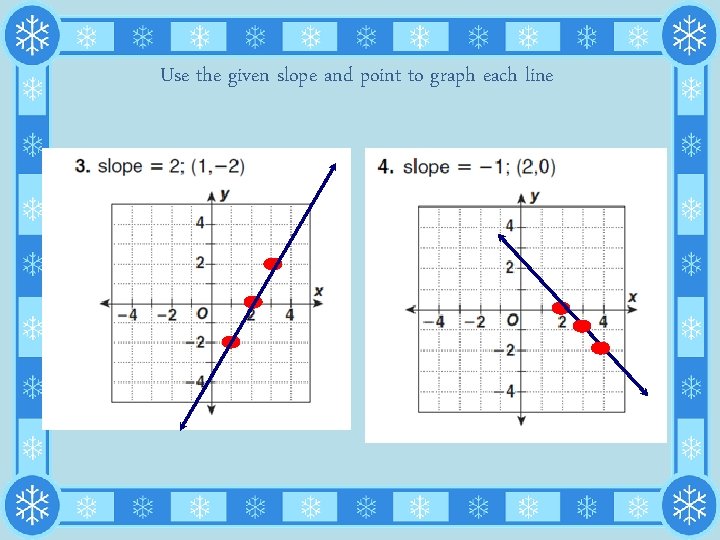
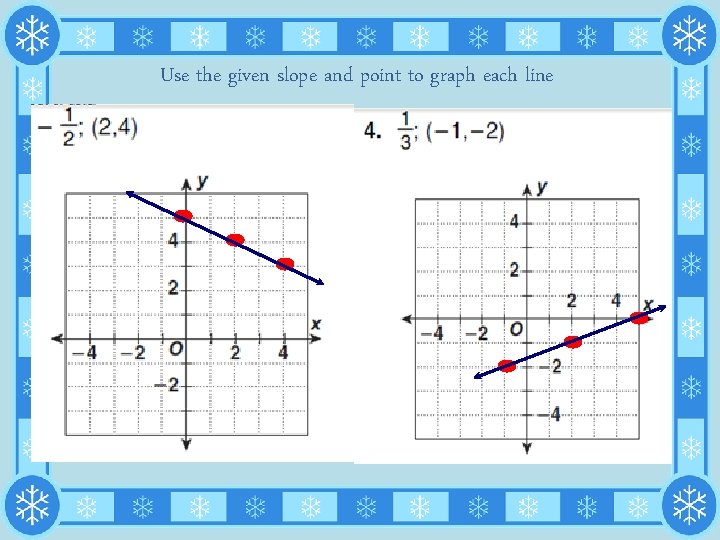
Use the given slope and point to graph each line

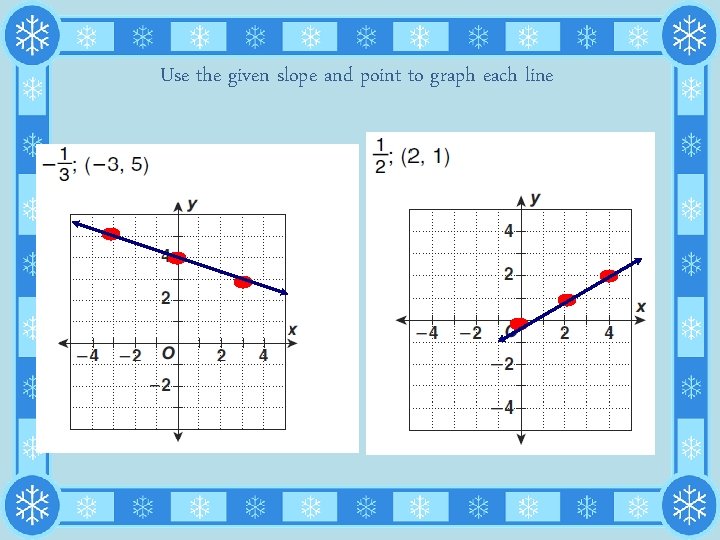
Use the given slope and point to graph each line

Use the given slope and point to graph each line

Rate of Change (Slope)

• . Rate of change (slope) describes how one quantity changes in relation to another. • For graphs, the rate of change (slope) is constant ( a straight line)

Tell whether each graph shows a constant or variable rate of change

Tell whether each graph shows a constant or variable rate of change

Tell whether each graph shows a constant or variable rate of change

Proportional Relationships

• A proportional relationship between two quantities is one in which the two quantities vary directly with one another (change the same way). This is called a direct variation. • For graphs, the rate of change (slope) is constant ( a straight line)
 2 6 rates ratios, and proportions answers
2 6 rates ratios, and proportions answers Ratios, rates, and proportions
Ratios, rates, and proportions 1-8 rates ratios and proportions
1-8 rates ratios and proportions 4-1 lesson quiz
4-1 lesson quiz Rates ratios and proportions
Rates ratios and proportions Ratios rates and unit rates guided notes
Ratios rates and unit rates guided notes Ratios rates and unit rates
Ratios rates and unit rates Ratios rates and unit rates
Ratios rates and unit rates What is a unit ratio
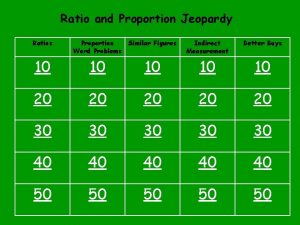
What is a unit ratio Jeopardy ratios
Jeopardy ratios How to write ratio
How to write ratio Trapezoid ratio and proportion
Trapezoid ratio and proportion 7-1 ratios and proportions
7-1 ratios and proportions Extended ratio geometry definition
Extended ratio geometry definition Proportions warm up
Proportions warm up 7-1 ratios & proportions
7-1 ratios & proportions 2-6 ratios and proportions
2-6 ratios and proportions Ratios and proportions review
Ratios and proportions review Quiz 1: ratios, properties, and proportions
Quiz 1: ratios, properties, and proportions If abcd is a rectangle and m adb=55 what is the value of x
If abcd is a rectangle and m adb=55 what is the value of x Ratios rates and conversions
Ratios rates and conversions What are ratios and rates
What are ratios and rates Ratios, rates, and conversions worksheet answers
Ratios, rates, and conversions worksheet answers Associated ratios and the value of a ratio
Associated ratios and the value of a ratio Chapter 22 comparing two proportions
Chapter 22 comparing two proportions Chapter 18 confidence intervals for proportions
Chapter 18 confidence intervals for proportions Module 5 proportions and percent
Module 5 proportions and percent Engineering economics and management
Engineering economics and management Similar figure proportions
Similar figure proportions Central limit theorem with proportions
Central limit theorem with proportions Chapter 22 comparing two proportions
Chapter 22 comparing two proportions Complex fractions and unit rates
Complex fractions and unit rates Sample proportion
Sample proportion Proportional sides
Proportional sides Which of these shapes is congruent to the given shape
Which of these shapes is congruent to the given shape Proportion portrait
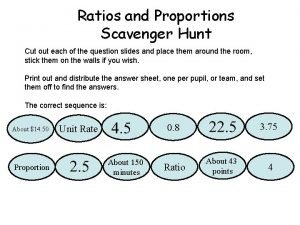
Proportion portrait Ratio scavenger hunt
Ratio scavenger hunt Les proportions stoechiométriques
Les proportions stoechiométriques A wise man proportions his belief to the evidence
A wise man proportions his belief to the evidence Core focus on proportions and probability answer key
Core focus on proportions and probability answer key Example of definite composition
Example of definite composition What is a proportion
What is a proportion Proportions jeopardy
Proportions jeopardy Would being part of a support group that meets regularly
Would being part of a support group that meets regularly Cross proportion
Cross proportion Chapter 20 testing hypotheses about proportions
Chapter 20 testing hypotheses about proportions Chapter 15 furniture styles and construction answer key
Chapter 15 furniture styles and construction answer key Pourcentage massique
Pourcentage massique