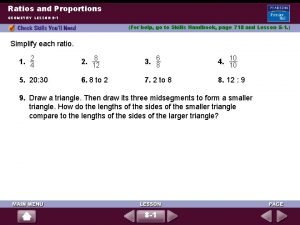
Proportions Proportions What are proportions If two ratios





- Slides: 12

Proportions

Proportions What are proportions? - If two ratios are equal, they form a proportion. Proportions can be used in geometry when working with similar figures. 1 4 2 = 8 1: 3 = 3: 9 What do we mean by similar? - Similar describes things which have the same shape but are not the same size.

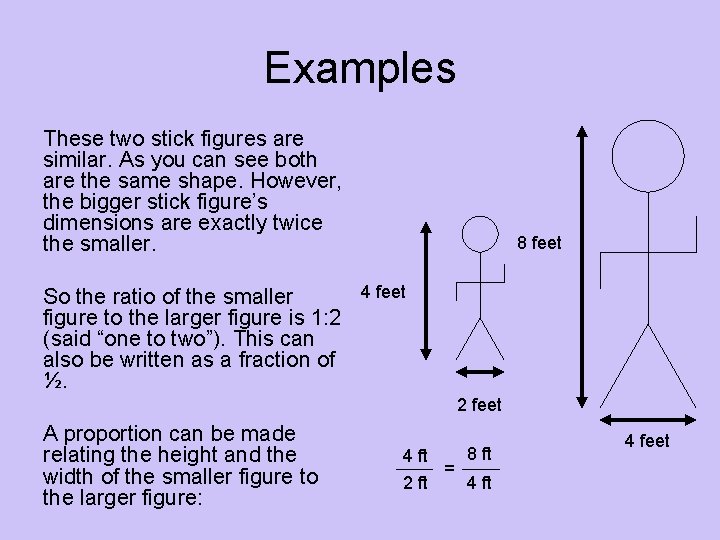
Examples These two stick figures are similar. As you can see both are the same shape. However, the bigger stick figure’s dimensions are exactly twice the smaller. 8 feet 4 feet So the ratio of the smaller figure to the larger figure is 1: 2 (said “one to two”). This can also be written as a fraction of ½. 2 feet A proportion can be made relating the height and the width of the smaller figure to the larger figure: 4 ft 2 ft = 8 ft 4 feet

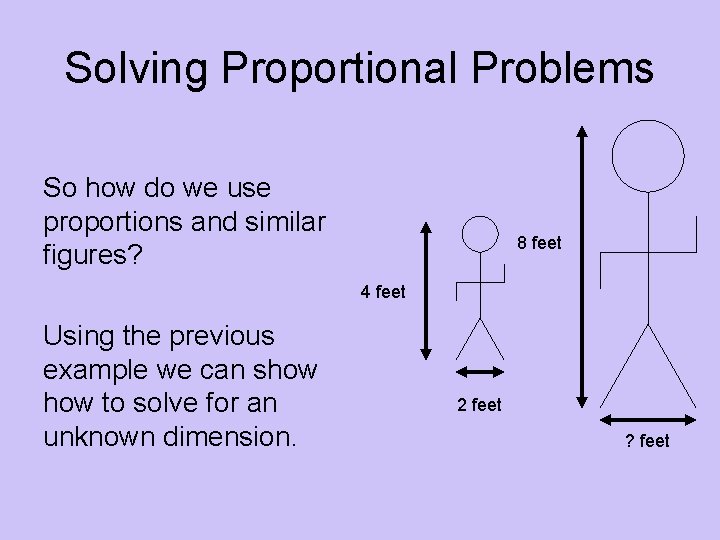
Solving Proportional Problems So how do we use proportions and similar figures? 8 feet 4 feet Using the previous example we can show to solve for an unknown dimension. 2 feet ? feet

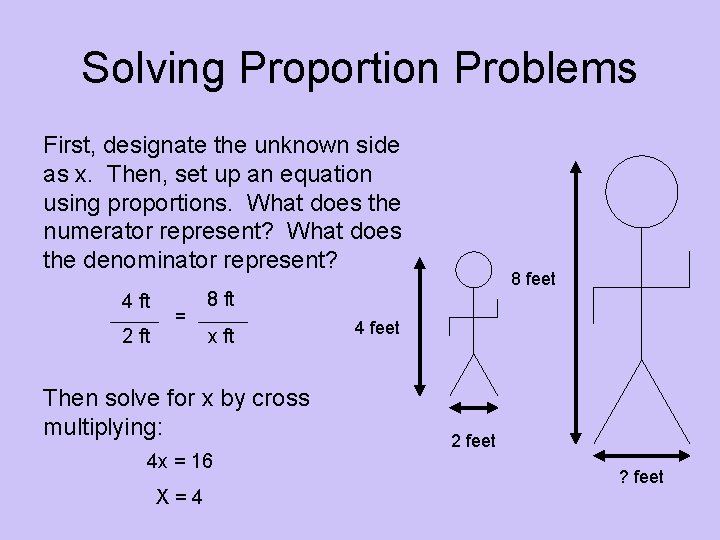
Solving Proportion Problems First, designate the unknown side as x. Then, set up an equation using proportions. What does the numerator represent? What does the denominator represent? 4 ft 2 ft = 8 ft x ft Then solve for x by cross multiplying: 4 x = 16 X=4 8 feet 4 feet 2 feet ? feet

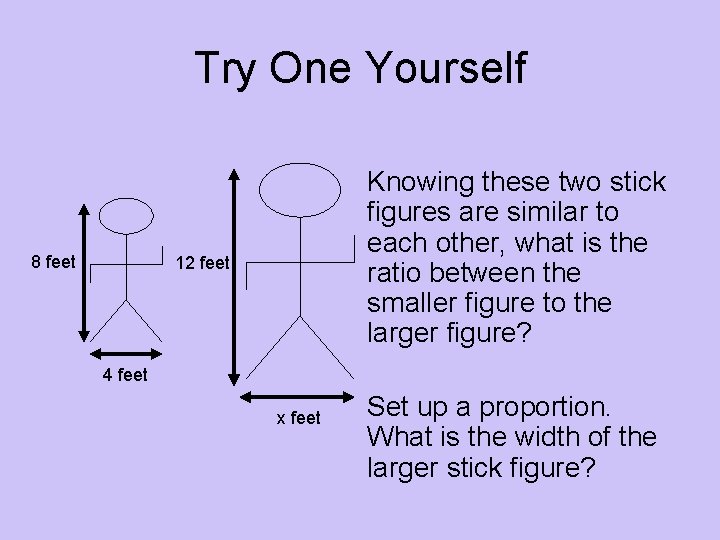
Try One Yourself 8 feet Knowing these two stick figures are similar to each other, what is the ratio between the smaller figure to the larger figure? 12 feet 4 feet x feet Set up a proportion. What is the width of the larger stick figure?

Similar Shapes In geometry similar shapes are very important. This is because if we know the dimensions of one shape and one of the dimensions of another shape similar to it, we can figure out the unknown dimensions.

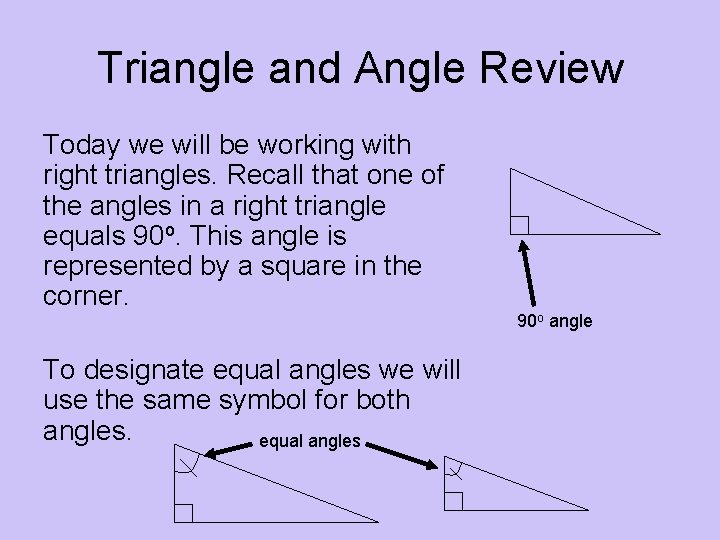
Triangle and Angle Review Today we will be working with right triangles. Recall that one of the angles in a right triangle equals 90 o. This angle is represented by a square in the corner. To designate equal angles we will use the same symbol for both angles. equal angles 90 o angle

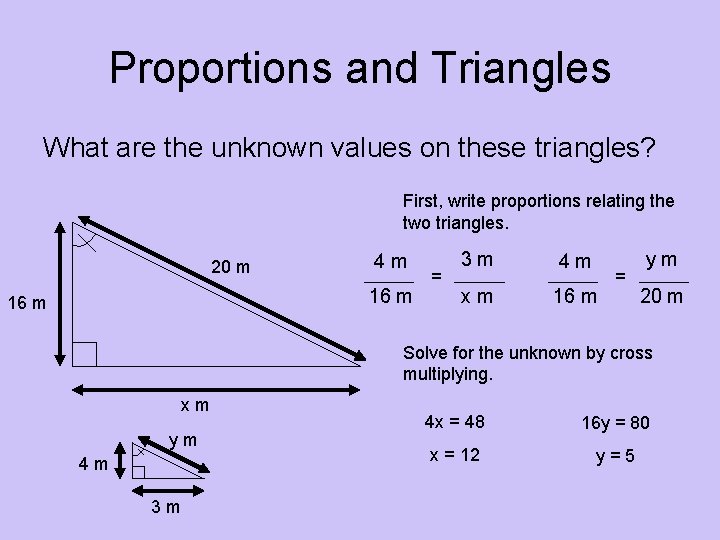
Proportions and Triangles What are the unknown values on these triangles? First, write proportions relating the two triangles. 20 m 4 m 16 m = 3 m 4 m xm 16 m = ym 20 m Solve for the unknown by cross multiplying. xm ym 4 m 3 m 4 x = 48 16 y = 80 x = 12 y=5

Triangles in the Real World Do you know how tall your school building is? There is an easy way to find out using right triangles. To do this create two similar triangles using the building, its shadow, a smaller object with a known height (like a yardstick), and its shadow. The two shadows can be measured, and you know the height of the yard stick. So you can set up similar triangles and solve for the height of the building.

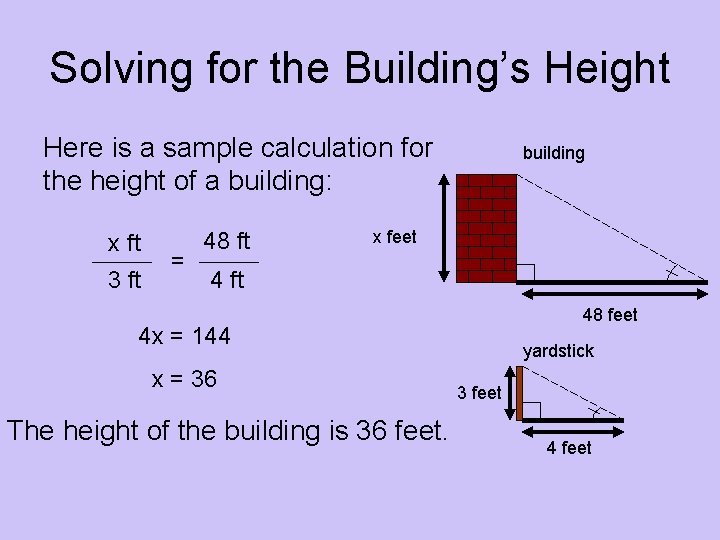
Solving for the Building’s Height Here is a sample calculation for the height of a building: x ft 3 ft = 48 ft building x feet 4 ft 48 feet 4 x = 144 x = 36 The height of the building is 36 feet. yardstick 3 feet 4 feet

Accuracy and Error Do you think using proportions to calculate the height of the building is better or worse than actually measuring the height of the building? Determine your height by the same technique used to determine the height of the building. Now measure your actual height and compare your answers. Were they the same? Why would there be a difference?
 Antigentest åre
Antigentest åre Practice 8-5 proportions in triangles
Practice 8-5 proportions in triangles Ratios, rates, and proportions
Ratios, rates, and proportions Ratio and proportion
Ratio and proportion 7-1 ratios & proportions
7-1 ratios & proportions Quiz 4-1 ratios rates and proportions answer key
Quiz 4-1 ratios rates and proportions answer key Proportion examples
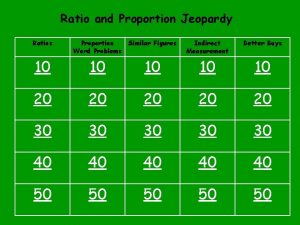
Proportion examples Ratio and proportion jeopardy
Ratio and proportion jeopardy 1-8 rates ratios and proportions
1-8 rates ratios and proportions Ratios and proportions geometry
Ratios and proportions geometry 7-1 ratios & proportions
7-1 ratios & proportions 2-6 ratios and proportions
2-6 ratios and proportions Homework 1 ratio and proportion
Homework 1 ratio and proportion