Ratios Proportions and Similar Figures Ratios proportions and









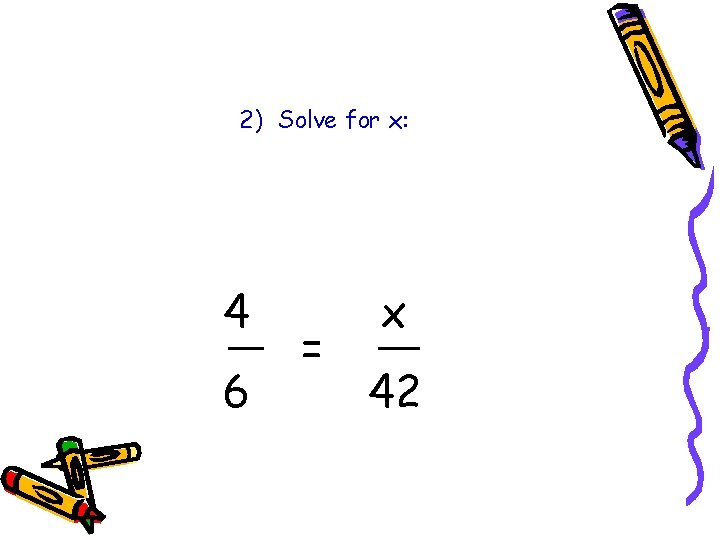



- Slides: 26

Ratios, Proportions and Similar Figures Ratios, proportions and scale drawings

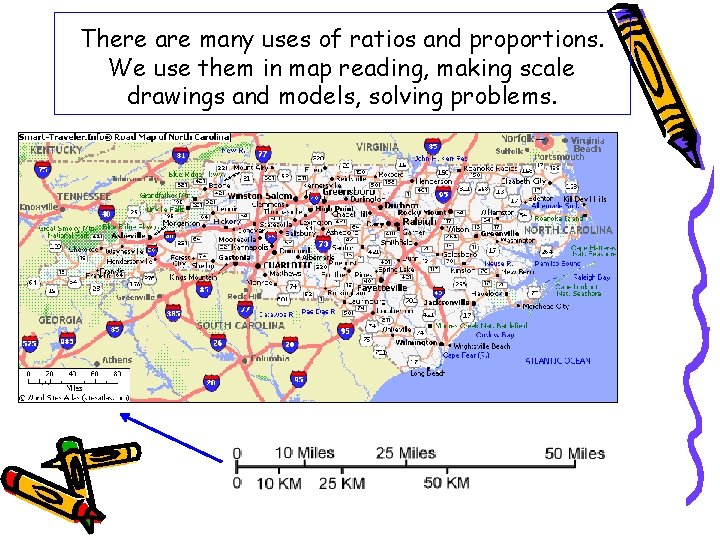
There are many uses of ratios and proportions. We use them in map reading, making scale drawings and models, solving problems.

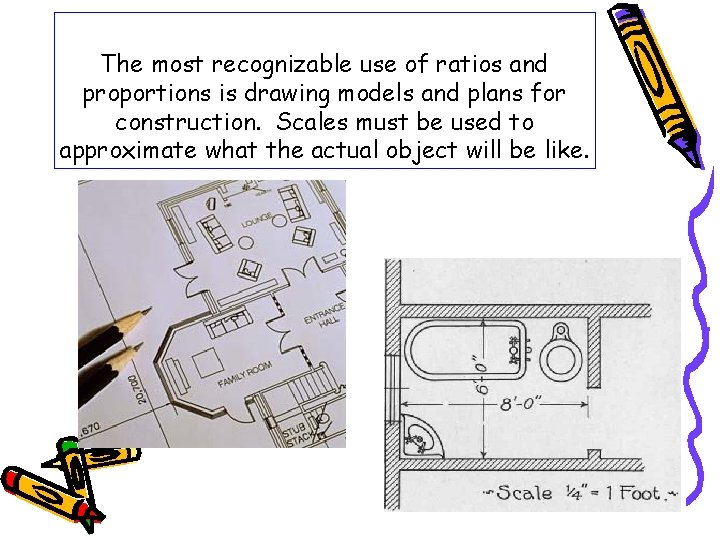
The most recognizable use of ratios and proportions is drawing models and plans for construction. Scales must be used to approximate what the actual object will be like.

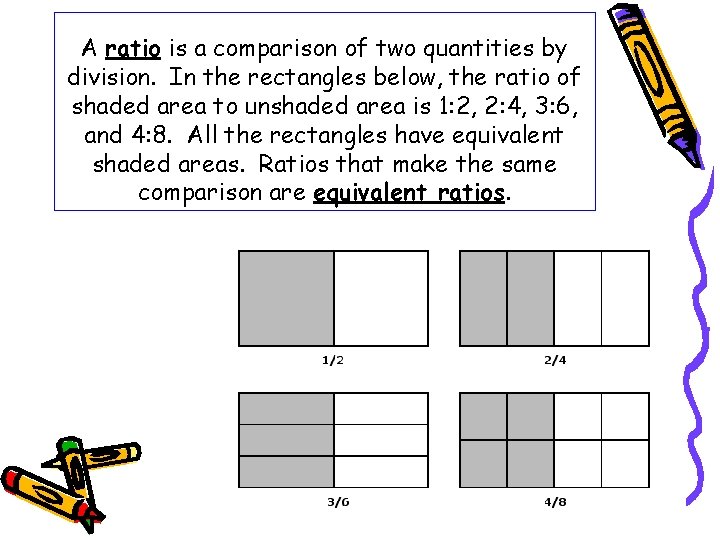
A ratio is a comparison of two quantities by division. In the rectangles below, the ratio of shaded area to unshaded area is 1: 2, 2: 4, 3: 6, and 4: 8. All the rectangles have equivalent shaded areas. Ratios that make the same comparison are equivalent ratios.

Using ratios The ratio of faculty members to students in one school is 1: 15. There are 675 students. How many faculty members are there? faculty 1 students 15 1 15 x = 675 15 x = 675 x = 45 faculty

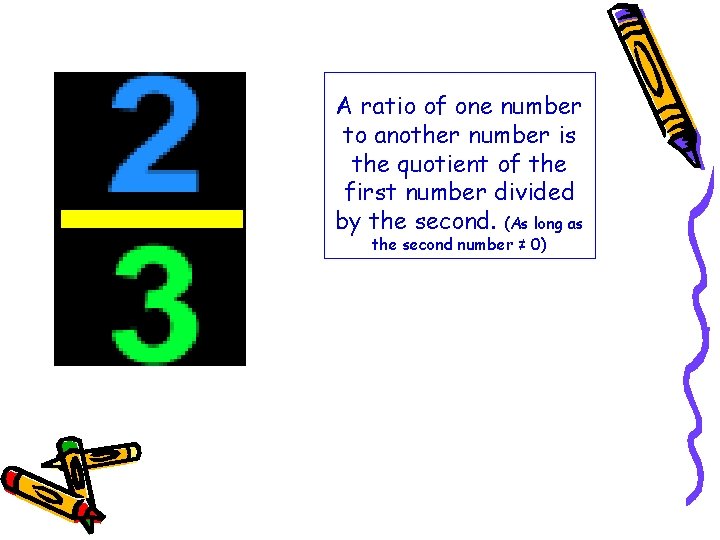
A ratio of one number to another number is the quotient of the first number divided by the second. (As long as the second number ≠ 0)

A ratio can be written in a variety of ways. You can use ratios to compare quantities or describe rates. Proportions are used in many fields, including construction, photography, and medicine. a: b a/b a to b

Since ratios that make the same comparison are equivalent ratios, they all reduce to the same value. 2 10 = 3 15 = 1 5

Proportions Two ratios that are equal

A proportion is an equation that states that two ratios are equal, such as:

In simple proportions, all you need to do is examine the fractions. If the fractions both reduce to the same value, the proportion is true. This is a true proportion, since both fractions reduce to 1/3. 5 15 = 2 6

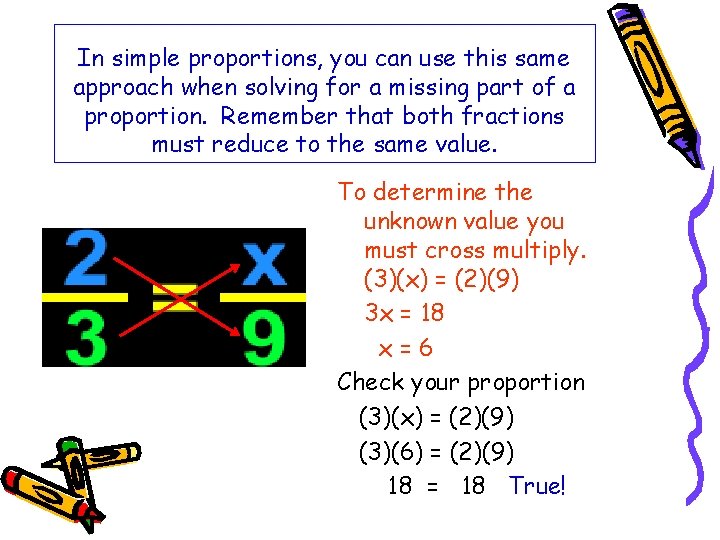
In simple proportions, you can use this same approach when solving for a missing part of a proportion. Remember that both fractions must reduce to the same value. To determine the unknown value you must cross multiply. (3)(x) = (2)(9) 3 x = 18 x=6 Check your proportion (3)(x) = (2)(9) (3)(6) = (2)(9) 18 = 18 True!

So, ratios that are equivalent are said to be proportional. Cross Multiply makes solving or proving proportions much easier. In this example 3 x = 18, x = 6. If you remember, this is like finding equivalent fractions when you are adding or subtracting fractions.

1) Are the following true proportions? 2 3 = 10 5 2 3 = 10 15
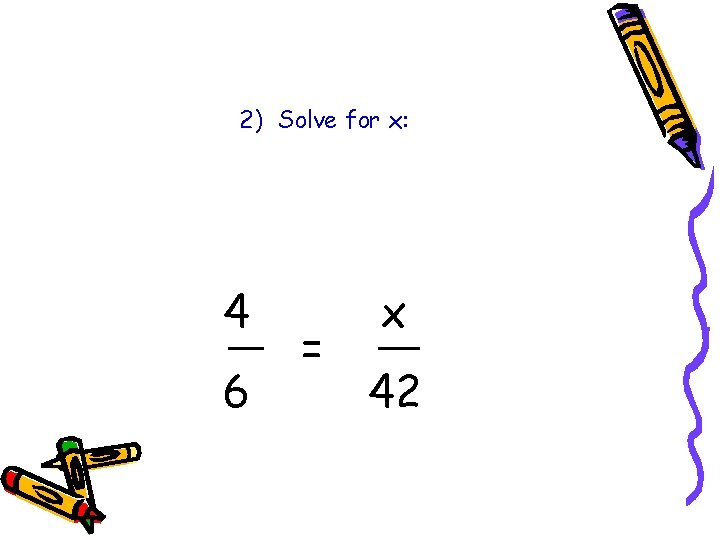
2) Solve for x: 4 6 = x 42

3) Solve for x: 25 x = 5 2

Solve the following problems. 4) If 4 tickets to a show cost $9. 00, find the cost of 14 tickets. 5) A house which is appraised for $10, 000 pays $300 in taxes. What should the tax be on a house appraised at $15, 000.

Similar Figures The Big and Small of it

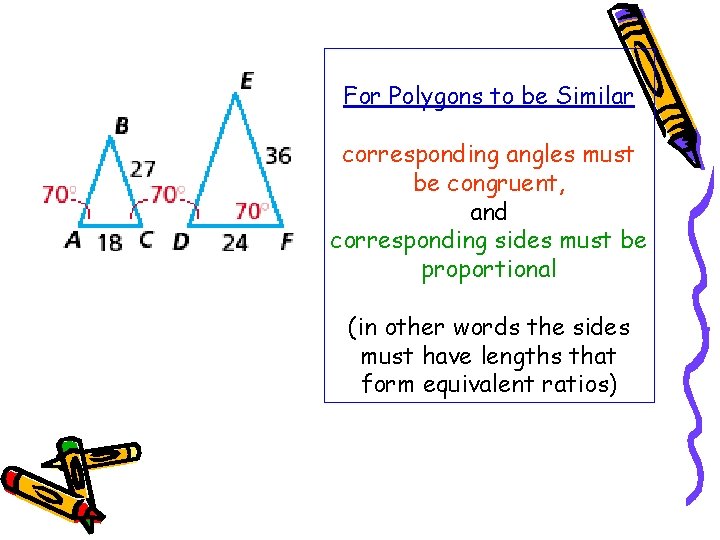
For Polygons to be Similar corresponding angles must be congruent, and corresponding sides must be proportional (in other words the sides must have lengths that form equivalent ratios)

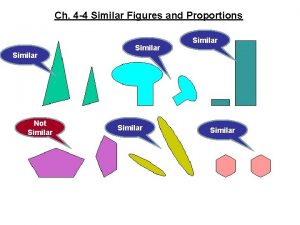
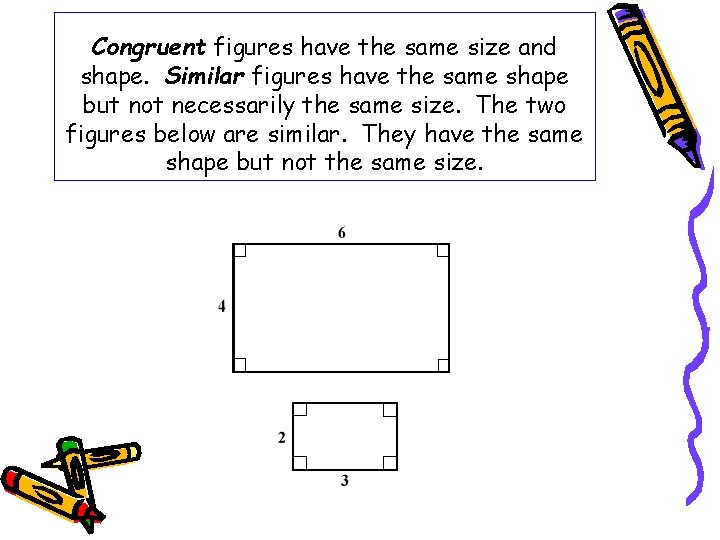
Congruent figures have the same size and shape. Similar figures have the same shape but not necessarily the same size. The two figures below are similar. They have the same shape but not the same size.

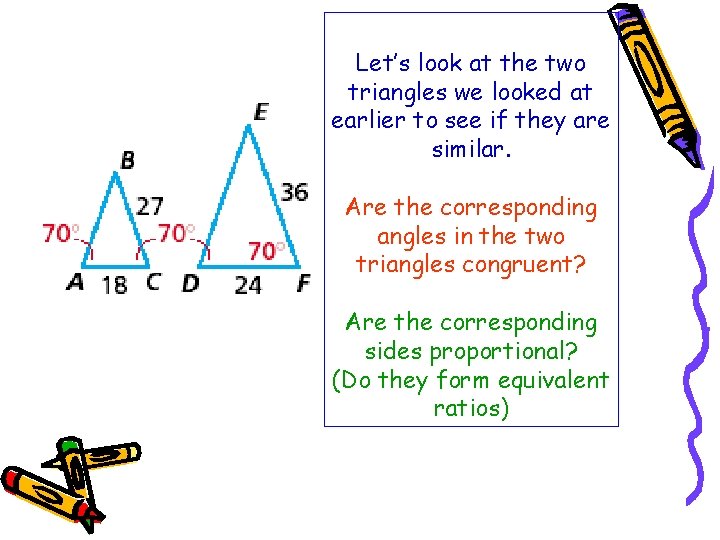
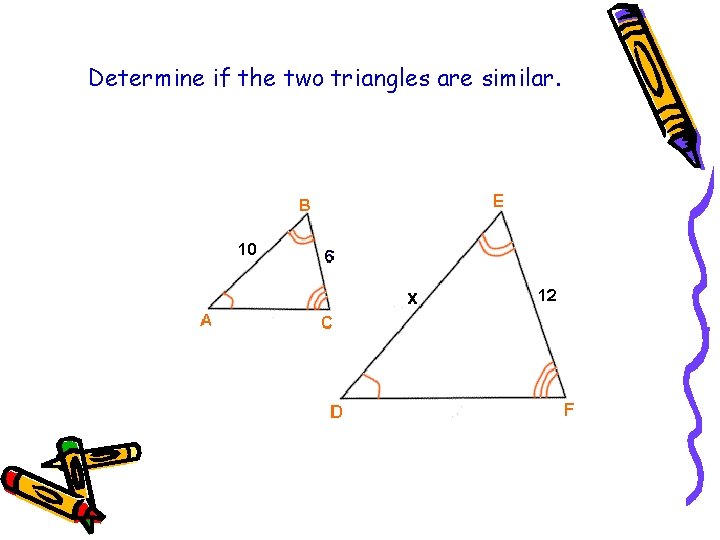
Let’s look at the two triangles we looked at earlier to see if they are similar. Are the corresponding angles in the two triangles congruent? Are the corresponding sides proportional? (Do they form equivalent ratios)

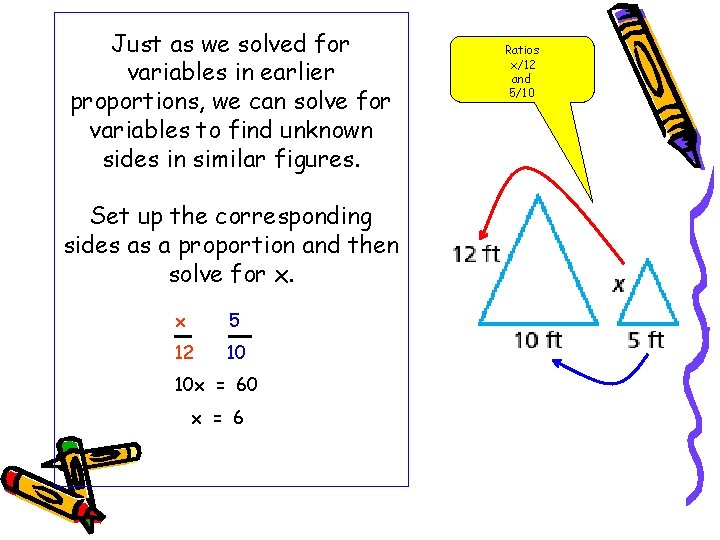
Just as we solved for variables in earlier proportions, we can solve for variables to find unknown sides in similar figures. Set up the corresponding sides as a proportion and then solve for x. x 5 12 10 10 x = 60 x = 6 Ratios x/12 and 5/10

Determine if the two triangles are similar.

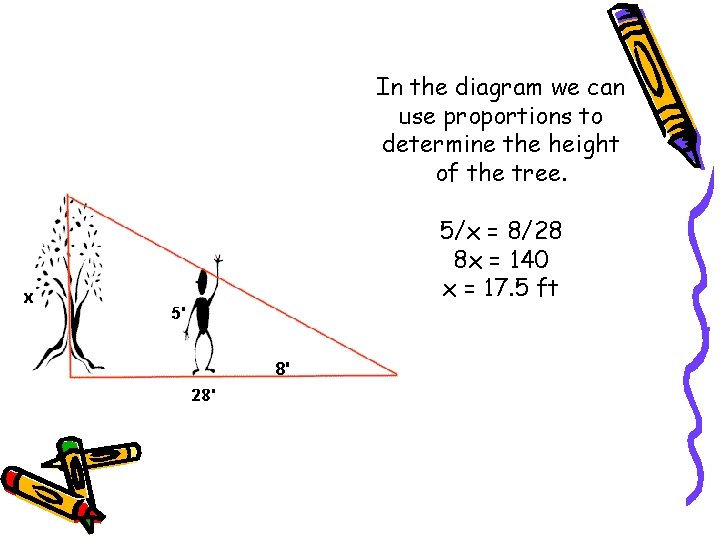
In the diagram we can use proportions to determine the height of the tree. 5/x = 8/28 8 x = 140 x = 17. 5 ft

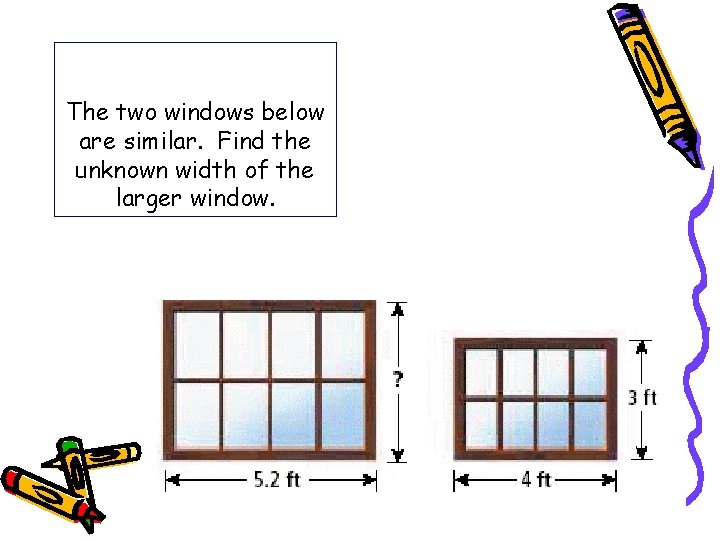
The two windows below are similar. Find the unknown width of the larger window.

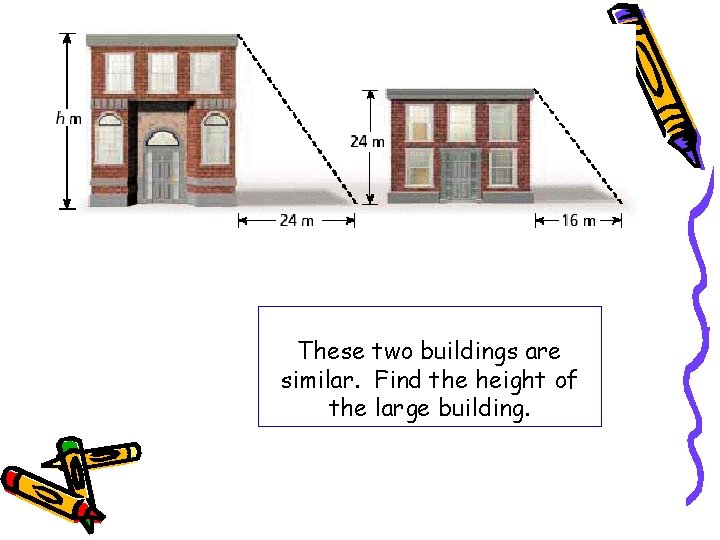
These two buildings are similar. Find the height of the large building.
 2-8 proportions and similar figures
2-8 proportions and similar figures Similar figures
Similar figures Similar shapes and proportions
Similar shapes and proportions 2-8 proportions and similar figures
2-8 proportions and similar figures Similar figure proportions
Similar figure proportions 7-1 ratios in similar polygons
7-1 ratios in similar polygons Quiz 6-1 ratios and similar figures
Quiz 6-1 ratios and similar figures Are all congruent figures similar
Are all congruent figures similar Practice 8-1 ratios and proportions answers
Practice 8-1 ratios and proportions answers Is a ratio a rate
Is a ratio a rate A to b ratio
A to b ratio 7-1 ratios and proportions
7-1 ratios and proportions Lesson quiz 4-2
Lesson quiz 4-2 Ratios and proportions review
Ratios and proportions review Proportion jeopardy
Proportion jeopardy Rates ratios and proportions
Rates ratios and proportions Similarity ratio
Similarity ratio 7 to 1 ratio
7 to 1 ratio Algebra 1 proportions
Algebra 1 proportions Quiz 1: ratios, properties, and proportions
Quiz 1: ratios, properties, and proportions What is a ratio notes
What is a ratio notes Equivalent ratios definition
Equivalent ratios definition 2-6 ratios and proportions
2-6 ratios and proportions 1-8 rates ratios and proportions
1-8 rates ratios and proportions Quiz 1 ratios properties and proportions
Quiz 1 ratios properties and proportions Which of these shapes is congruent to the given shape?
Which of these shapes is congruent to the given shape? Area of similar shapes worksheet
Area of similar shapes worksheet