COMP 319 Algorithm Analysis Franklin University Module 4

COMP 319 Algorithm Analysis Franklin University Module 4: The Greedy Method 1

COMP 319 Algorithm Analysis Franklin University What are Greedy algorithms? • Greedy algorithms are quite simple. • Typically used to solve optimization problems (problems that have many possible solutions and each solution has a cost). • Finds a solution by making a sequence of choices. • At each step of the algorithm, a choice that seems best at the moment is chosen without any thinking ahead or backtracking. • Once a candidate is included in the solution, it is there for good. Once a candidate is excluded from the solution, it is never considered again. 2

COMP 319 Algorithm Analysis Franklin University Some Greedy Algorithms • • • Prim's Kruskal's Dijkstra's Single-Source Shortest Path Scheduling The Knapsack Problem 3

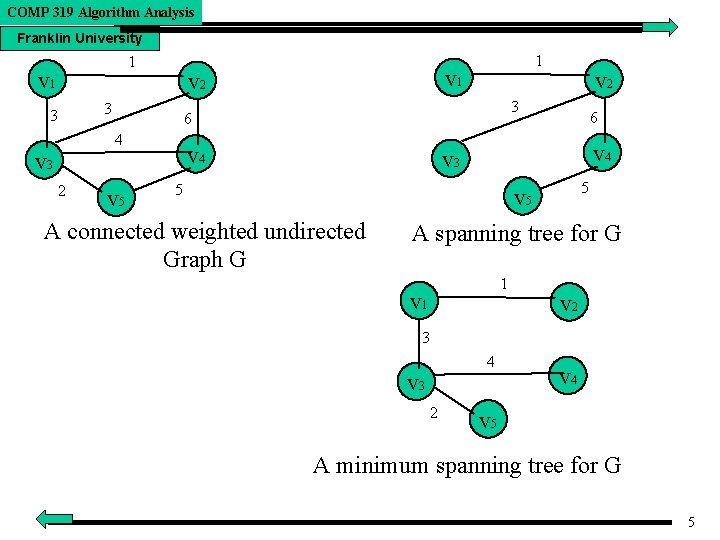
COMP 319 Algorithm Analysis Franklin University Minimum Cost Spanning Trees • Prim’s and Kruskal’s Algorithms (which are greedy algorithms) find minimum cost spanning trees. • A spanning tree consists of the least number of edges needed to link all vertices in any given graph. For any graph, there are possibly many spanning trees. • A minimum cost spanning tree is a spanning tree of least or minimum cost. • Examples of use of minimum cost spanning trees in the real world: using the minimum length of cable possible in setting up a telecommunications network; using the minimal length of pipe in designing a plumbing system. 4

COMP 319 Algorithm Analysis Franklin University 1 v 1 3 3 v 1 v 2 3 6 4 v 3 1 v 4 6 v 4 v 3 5 v 5 A connected weighted undirected Graph G 2 5 v 5 A spanning tree for G 1 v 2 3 4 v 3 2 v 4 v 5 A minimum spanning tree for G 5

COMP 319 Algorithm Analysis Franklin University Kruskal’s Algorithm: • Adds edges to the minimum cost spanning tree, one edge at a time. • Adds edges in increasing order of cost, cheapest edge first, next cheapest next, etc. • Does not allow cycles. • Time complexity (m log m) (m = number of edges) Prim’s Algorithm: • Constructs the minimum cost spanning tree one edge at a time starting with any of the vertices in the original graph. • Selects an additional edge so that the set of selected edges forms a tree (this edge must be of least cost). • Does not allow cycles. • Repeats edge addition until the final tree contains n-1 edges. 6

COMP 319 Algorithm Analysis Franklin University High-level algorithm for Kruskal's approach F = ; // Initialize set of edges to empty Create disjoint subsets of V, one for each vertex and containing only that vertex; Sort the edges E in nondecreasing order; While (the instance is not solved) { Select next edge; // Selection procedure // feasibility check if (the edge connects two vertices in disjoint subsets) { merge the subsets add the edge to F; }; if (all the subsets are merged) the instance is solved; } 7

COMP 319 Algorithm Analysis Franklin University Kruskal's algorithm using C++ like pseudocode Void Kruskal (int n, int m, set_of_edges E, set_of_edges& F) { index i, j; set_pointer p, q; edge e; sort the m edges in E by weights in nondecreasing order F = ; initialize (n) // initialize n disjoint subsets; while ( number of edges in F is less than n – 1) { e = edge with least weight not yet considered; i, j = indices of vertices connected by e; p = find (i); q = find (j); if (! equal (p, q)){ merge (p, q) ; add e to F; } } 8

COMP 319 Algorithm Analysis Franklin University High-level algorithm for Prim's approach F = ; Y = {v 1} While (the instance is not solved) { select a vertex in V - Y that is nearest to Y; add the vertex to Y; add the edge to F; if (Y == V) the instance is solved; } 9

COMP 319 Algorithm Analysis Franklin University Prim's algorithm using C++ like pseudocode void prim( int n, const number W[][], set_of_edges& F) { index i, vnear; number min; edge e; index nearest[2. . n]; number distance[2. . n]; F = ; for (i = 2; i<= n; i++) { nearest[i] = 1; distance[i] = W[1][i]; } 10

COMP 319 Algorithm Analysis Franklin University Prim's algorithm using C++ like pseudocode repeat (n-1) times { min = inf; for ( i = 2; i<= n; i++) if (0 <= distance[i] < min) { min = distance[i]; vnear = i; } e = edge connecting vertices indexed by vnear and nearest[vnear]; add e to F; distance[vnear] = -1; 11

COMP 319 Algorithm Analysis Franklin University Prim's algorithm using C++ like pseudocode for ( i = 2; i <= n; i++) if (W[i][vnear] < distance[i] { distance[i] = W[i][vnear]; nearest[i] = vnear; } } } 12

COMP 319 Algorithm Analysis Franklin University Sollin’s algorithm: • Another algorithm for finding the minimum cost spanning tree. • Selects several edges for inclusion into the minimum cost spanning tree at every stage of the algorithm. • Selects one edge for each tree in the forest (this edge must be of minimum cost). • Does not allow cycles. 13

COMP 319 Algorithm Analysis Franklin University Dijkstra's Single-Source Shortest Path Y = {v 1} While (the instance is not solved) { // Selection procedure // and feasibility check Select a vertex v from V - Y, that has shortest path from v 1, using only vertices in Y as intermediates add the new vertex v to Y; } if (Y == V) //solution check the instance is solved 14

COMP 319 Algorithm Analysis Franklin University Dijkstra's Single-Source Shortest Path void dijkstra (int n, const number W[][], number length[]) { index i, vnear; index touch[2. . n]; number length[2. . n]; boolean Y[2. . n]; // if a node is present in Y for (i = 2; i<= n; i++) { touch[i] = 1; Y[i] = False; length[i] = W[1][i]; } 15

COMP 319 Algorithm Analysis Franklin University Dijkstra's Single-Source Shortest Path repeat (n-1) times { min = ; for (i = 2; i<= n; i++) if (Y[i] == False) if (length[i] < min { min = length[i]; vnear = i; } Y[vnear] = True; for (i = 2; i <= n; i++) { if (Y[i] == False) if (length[vnear] + W[vnear][i] < length[i]) { length[i] = length[vnear] + W[near][i]; touch[i] = vnear; } } } 16

COMP 319 Algorithm Analysis Franklin University Scheduling: A Simple Scheduling Problem • Minimizing Total Time in the System Suppose there are three jobs and the service times for these jobs are t 1 = 5, t 2 = 10, and t 3 = 4. If we schedule them in the order job 1, job 2, job 3, the times spent in the system for the three jobs are a s follows: Job 1 2 3 Time in the System 5 (service time) 5 (wait for job 1) + 10 (wait for job 2) + 4 (service time) The total time in the system for this schedule is = 39. 17

COMP 319 Algorithm Analysis Franklin University Minimizing Total Time: contd. • The list of all possible schedules from our example: Schedule [1, 2, 3] [1, 3, 2] [2, 1, 3] [2, 3, 1] [3, 1, 2] [3, 2, 1] Total Time in System 5 + (5+10) + (5+10+4) = 39 5 + (5+4) + (5+4+10) = 33 10 + (10+5) + (10+5+4) = 44 10 + (10+4) + (10+4+5) = 43 4 + (4+5) + (4+5+10) = 32 4 + (4+10) + (4+10+5) = 37 Schedule [3, 1, 2] is the optimal schedule with the minimum total time of 32. 18

COMP 319 Algorithm Analysis Franklin University Scheduling Sort the jobs by service time in non decreasing order While (the instance is not solved ( { schedule the next job if (there are no more jobs) the instance is solve } • Shortest job scheduling is optimal scheduling • Time complexity (n log n) 19

COMP 319 Algorithm Analysis Franklin University 0 -1 Knapsack Problem: A Greedy Approach • Problem: A thief breaks into a jewelry store with a knapsack. The knapsack will break if the total weight of stolen items exceeds some minimum weight W. Each item has a value and a weight. The problem is to maximize the total value of the items while not making the total weight exceed W. • Steal items with the largest profit first. That is, steal items in non increasing order according to profit. Suppose there are three items with the following weights and profits: item 1: 25 lbs. $10 item 2: 10 lbs. $9 item 3: 10 lbs. $9 and capacity W of knapsack is 30 lbs. Then this greedy strategy will yield a profit of $10, whereas the optimal profit is $18. • Steal lightest items first: This strategy fails badly when lighter items have small profits compared with their weights. 20

COMP 319 Algorithm Analysis Franklin University • Steal items with the largest profit per unit first: Order items in non increasing order according to profit per unit weight, and select them in sequence. • W = 30 lbs. Weights and profits: item 1: $50 5 lbs. item 2: $60 10 lbs; item 3: $140 20 lbs. Profits per unit weight: item 1: $50/5 = $10; item 2: $60/10 = $6; item 3: $140/20 = $7 Knapsack Greedy Solution Optimal Solution 5 lbs. Wasted 30 lbs. Max. 20 lbs. 10 lbs. 5 lbs. 21

COMP 319 Algorithm Analysis Franklin University 0 -1 Knapsack Problem: Dynamic Programming Time Complexity for Optimal Solution: Brute-force algorithm: (2 n) Dynamic Programming : (n W) P[i][w]: The optimal profit obtained when choosing items only from the first i items under the restriction that the total weight can not exceed w P[i][w] = maximum( P[i-1][w], pi + P[i-1][w - wi] ) if wi <= w = P[i-1][w] P[0][w] = 0 P[i][0] = 0 if wi > w 22

COMP 319 Algorithm Analysis Franklin University 0 -1 Knapsack Problem: Dynamic Programming • Refinement of Dynamic Programming Algorithm for 0 -1 knapsack problem - It is not necessary to determine the entries in the ith row for every w between 1 to W • Determine entries needed for row 3: We need P[3][W] = P[3][30] • Determine entries needed for row 2: To compute P[3][30], we need P[3 -1][30] = P[2][30] and P[3 -1][30 - w 3] = P[2][10] 23

COMP 319 Algorithm Analysis Franklin University 0 -1 Knapsack Problem: Dynamic Programming • Determine entries needed for row 1: To compute P[2][30], we need P[2 -1][30] = P[1][30] and P[2 -1][30 - w 2] = P[1][20] To compute P[2][10], we need P[2 -1][10] = P[1][10] and P[2 -1][10 - w 2] = P[1][0] 24

COMP 319 Algorithm Analysis Franklin University 0 -1 Knapsack Problem: Dynamic Programming Next we do the computation: Row 1: P[1][0] = 0 P[1][10] = 50 P[1][20] = 50 P[1][30] = 50 Row 2: P[2][10] = ? P[2][30] = ? Row 3: P[3][30]? 25

COMP 319 Algorithm Analysis Franklin University Fractional Knapsack Problem • The thief does not have to steal all of an item, but rather can take any fraction of the item. • The greedy strategy is again to choose the items with largest profit per unit weight first. • Total profit: $50 + $140 + 5/10($60) = $220 • Greedy strategy always yields an optimal solution for rational knapsack problem. 26