Algorithm Analysis 1 Algorithm An algorithm is a

Algorithm Analysis 1

Algorithm • An algorithm is a set of instructions to be followed to solve a problem. – There can be more than one solution (more than one algorithm) to solve a given problem. – An algorithm can be implemented using different programming languages on different platforms. • An algorithm must be correct. It should correctly solve the problem. • Once we have a correct algorithm for a problem, we have to determine the efficiency of that algorithm. 2

Algorithmic Performance There are two aspects of algorithmic performance: • Time • Instructions take time. • How fast does the algorithm perform? • What affects its runtime? • Space • Data structures take space • What kind of data structures can be used? • How does choice of data structure affect the runtime? Ø We will focus on time: – How to estimate the time required for an algorithm – How to reduce the time required 3

Analysis of Algorithms • When we analyze algorithms, we should employ mathematical techniques that analyze algorithms independently of specific implementations, computers, or data. • To analyze algorithms: – First, we start to count the number of significant operations in a particular solution to assess its efficiency. – Then, we will express the efficiency of algorithms using growth functions. 4

The Execution Time of Algorithms • Each operation in an algorithm (or a program) has a cost. Each operation takes a certain of time. count = count + 1; take a certain amount of time, but it is constant A sequence of operations: count = count + 1; sum = sum + count; Cost: c 1 Cost: c 2 Total Cost = c 1 + c 2 5

The Execution Time of Algorithms (cont. ) Example: Simple If-Statement if (n < 0) absval = -n else absval = n; Cost c 1 c 2 c 3 Times 1 1 1 Total Cost <= c 1 + max(c 2, c 3) 6

The Execution Time of Algorithms (cont. ) Example: Simple Loop i = 1; sum = 0; while (i <= n) { i = i + 1; n sum = sum + i; } Cost c 1 c 2 c 3 Times 1 1 n+1 c 4 c 5 n Total Cost = c 1 + c 2 + (n+1)*c 3 + n*c 4 + n*c 5 The time required for this algorithm is proportional to n 7

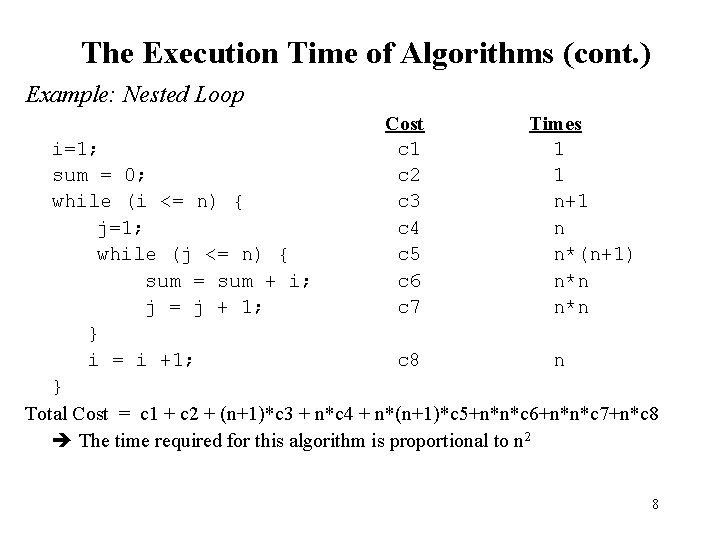
The Execution Time of Algorithms (cont. ) Example: Nested Loop Cost c 1 c 2 c 3 c 4 c 5 c 6 c 7 Times 1 1 n+1 n n*(n+1) n*n i=1; sum = 0; while (i <= n) { j=1; while (j <= n) { sum = sum + i; j = j + 1; } i = i +1; c 8 n } Total Cost = c 1 + c 2 + (n+1)*c 3 + n*c 4 + n*(n+1)*c 5+n*n*c 6+n*n*c 7+n*c 8 The time required for this algorithm is proportional to n 2 8

General Rules for Estimation • Loops: The running time of a loop is at most the running time of the statements inside of that loop times the number of iterations. • Nested Loops: Running time of a nested loop containing a statement in the inner most loop is the running time of statement multiplied by the product of the sized of all loops. • Consecutive Statements: Just add the running times of those consecutive statements. 9

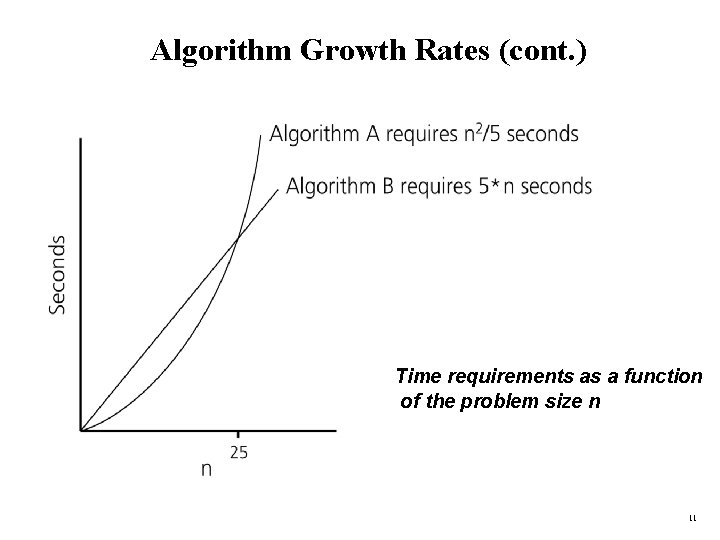
Algorithm Growth Rates • We measure an algorithm’s time requirement as a function of the problem size. – Problem size depends on the application: e. g. number of elements in a list for a sorting algorithm. • So, for instance, we say that (if the problem size is n) – Algorithm A requires 5*n 2 time units to solve a problem of size n. – Algorithm B requires 7*n time units to solve a problem of size n. • The most important thing to learn is how quickly the algorithm’s time requirement grows as a function of the problem size. – Algorithm A requires time proportional to n 2. – Algorithm B requires time proportional to n. • An algorithm’s proportional time requirement is known as growth rate. • We can compare the efficiency of two algorithms by comparing their growth rates. CENG 213 Data Structures 10

Algorithm Growth Rates (cont. ) Time requirements as a function of the problem size n 11

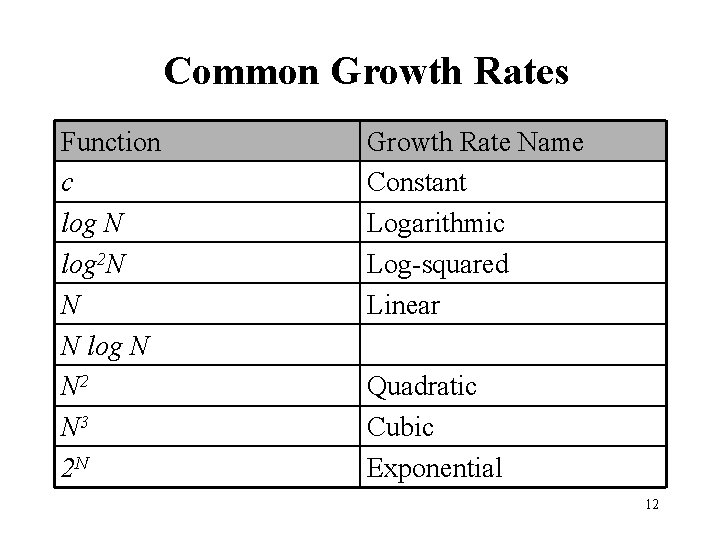
Common Growth Rates Function c log N log 2 N N N log N N 2 N 3 2 N Growth Rate Name Constant Logarithmic Log-squared Linear Quadratic Cubic Exponential 12

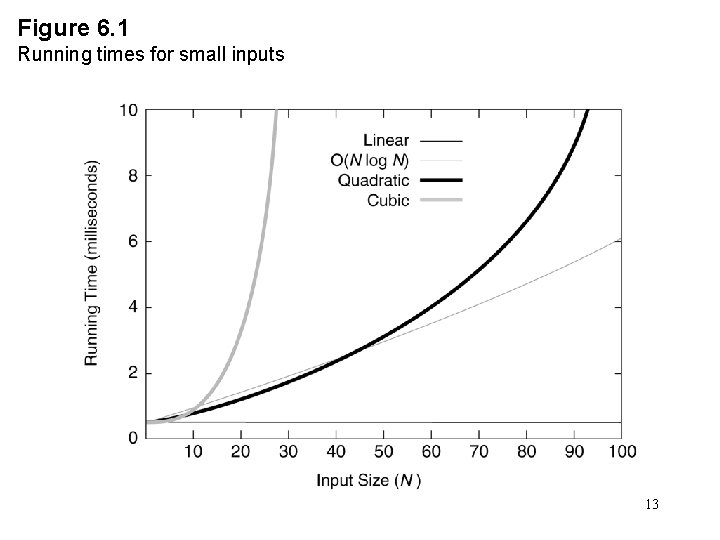
Figure 6. 1 Running times for small inputs 13

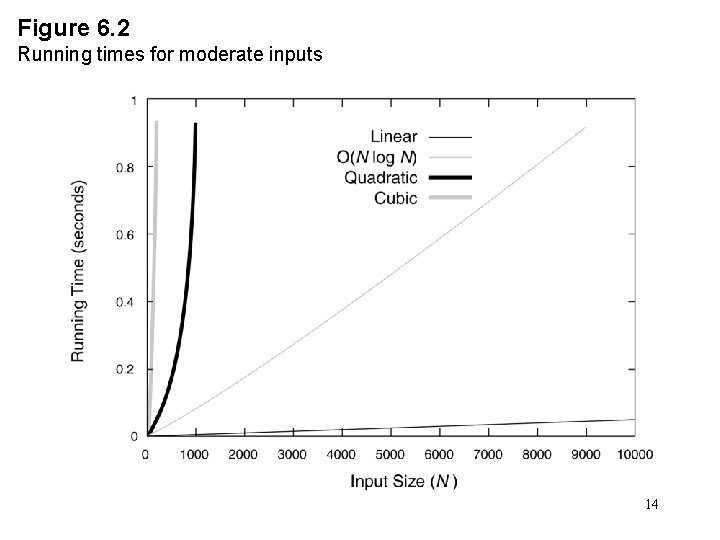
Figure 6. 2 Running times for moderate inputs 14

Order-of-Magnitude Analysis and Big O Notation • If Algorithm A requires time proportional to f(n), Algorithm A is said to be order f(n), and it is denoted as O(f(n)). • The function f(n) is called the algorithm’s growth-rate function. • Since the capital O is used in the notation, this notation is called the Big O notation. • If Algorithm A requires time proportional to n 2, it is O(n 2). • If Algorithm A requires time proportional to n, it is O(n). 15

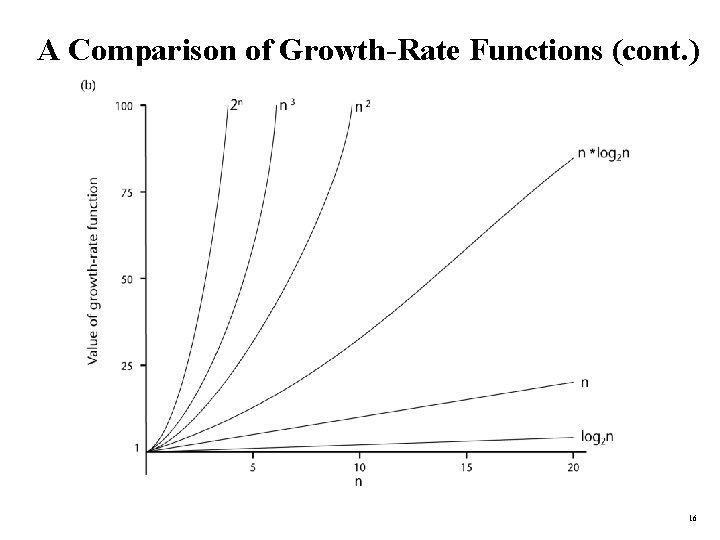
A Comparison of Growth-Rate Functions (cont. ) 16

Growth-Rate Functions O(1) O(log 2 n) Time requirement is constant, and it is independent of the problem’s size. Time requirement for a logarithmic algorithm increases slowly as the problem size increases. O(n) Time requirement for a linear algorithm increases directly with the size of the problem. O(n*log 2 n) Time requirement for a n*log 2 n algorithm increases more rapidly than a linear algorithm. O(n 2) Time requirement for a quadratic algorithm increases rapidly with the size of the problem. O(n 3) Time requirement for a cubic algorithm increases more rapidly with the size of the problem than the time requirement for a quadratic algorithm. O(2 n) As the size of the problem increases, the time requirement for an exponential algorithm increases too rapidly to be practical. CENG 213 Data Structures 17

Growth-Rate Functions • If an algorithm takes 1 second to run with the problem size 8, what is the time requirement (approximately) for that algorithm with the problem size 16? • If its order is: O(1) T(n) = 1 second O(log 2 n) T(n) = (1*log 216) / log 28 = 4/3 seconds O(n) T(n) = (1*16) / 8 = 2 seconds O(n*log 2 n) T(n) = (1*16*log 216) / 8*log 28 = 8/3 seconds O(n 2) T(n) = (1*162) / 82 = 4 seconds O(n 3) T(n) = (1*163) / 83 = 8 seconds O(2 n) T(n) = (1*216) / 28 = 28 seconds = 256 seconds 18

Properties of Growth-Rate Functions 1. We can ignore low-order terms in an algorithm’s growth-rate function. – If an algorithm is O(n 3+4 n 2+3 n), it is also O(n 3). – We only use the higher-order term as algorithm’s growth-rate function. 2. We can ignore a multiplicative constant in the higher-order term of an algorithm’s growth-rate function. – If an algorithm is O(5 n 3), it is also O(n 3). 3. O(f(n)) + O(g(n)) = O(f(n)+g(n)) – We can combine growth-rate functions. – If an algorithm is O(n 3) + O(4 n), it is also O(n 3 +4 n 2) So, it is O(n 3). – Similar rules hold for multiplication. 19

Some Mathematical Facts • Some mathematical equalities are: 20

Growth-Rate Functions – Example 1 i = 1; sum = 0; while (i <= n) { i = i + 1; n sum = sum + i; } Cost c 1 c 2 c 3 Times 1 1 n+1 c 4 c 5 n T(n) = c 1 + c 2 + (n+1)*c 3 + n*c 4 + n*c 5 = (c 3+c 4+c 5)*n + (c 1+c 2+c 3) = a*n + b So, the growth-rate function for this algorithm is O(n) 21

Growth-Rate Functions – Example 2 Cost c 1 c 2 c 3 c 4 c 5 c 6 c 7 Times 1 1 n+1 n n*(n+1) n*n i=1; sum = 0; while (i <= n) { j=1; while (j <= n) { sum = sum + i; j = j + 1; } i = i +1; c 8 n } T(n) = c 1 + c 2 + (n+1)*c 3 + n*c 4 + n*(n+1)*c 5+n*n*c 6+n*n*c 7+n*c 8 = (c 5+c 6+c 7)*n 2 + (c 3+c 4+c 5+c 8)*n + (c 1+c 2+c 3) = a*n 2 + b*n + c So, the growth-rate function for this algorithm is O(n 2) 22

What to Analyze • An algorithm can require different times to solve different problems of the same size. – Eg. Searching an item in a list of n elements using sequential search. Cost: 1, 2, . . . , n • Worst-Case Analysis –The maximum amount of time that an algorithm require to solve a problem of size n. – This gives an upper bound for the time complexity of an algorithm. – Normally, we try to find worst-case behavior of an algorithm. • Best-Case Analysis –The minimum amount of time that an algorithm require to solve a problem of size n. – The best case behavior of an algorithm is NOT so useful. • Average-Case Analysis –The average amount of time that an algorithm require to solve a problem of size n. – Sometimes, it is difficult to find the average-case behavior of an algorithm. – We have to look at all possible data organizations of a given size n, and their distribution probabilities of these organizations. – Worst-case analysis is more common than average-case analysis. 23

What is Important? • An array-based list retrieve operation is O(1), a linked-listbased list retrieve operation is O(n). • But insert and delete operations are much easier on a linked-listbased list implementation. When selecting the implementation of an Abstract Data Type (ADT), we have to consider how frequently particular ADT operations occur in a given application. • If the problem size is always small, we can probably ignore the algorithm’s efficiency. – In this case, we should choose the simplest algorithm. 24

Sequential Search for i = 1 to N do if (target == list[i]) return i end if end for return 0 // Not found Unsuccessful Search: O(n) Successful Search: Best-Case: item is in the first location of the array O(1) Worst-Case: item is in the last location of the array O(n) 25

Binary Search • • • • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 int first = 0; int size ; int last = size – 1; int middle; boolean found = false; while ( first <= last && !found ) { middle = ( first + last ) /2 ; if ( item. To. Find == A[ middle ] ) found = true; else if ( item. To. Find < A[ middle ] ) last = middle – 1; else // item. To. Find > A[ middle ] first = middle + 1; } 26

Binary Search – Analysis • For an unsuccessful search: – The number of iterations in the loop is log 2 n + 1 O(log 2 n) • For a successful search: – Best-Case: The number of iterations is 1. – Worst-Case: The number of iterations is log 2 n +1 – Average-Case: The avg. # of iterations < log 2 n O(1) O(log 2 n) 27

How much better is O(log 2 n)? n 16 64 256 1024 (1 KB) 16, 384 131, 072 262, 144 524, 288 1, 048, 576 (1 MB) 1, 073, 741, 824 (1 GB) O(log 2 n) 4 6 8 10 14 17 18 19 20 30 28

Bubble Sorting Algorithm Analysis Algorithm: Input array of size N for(i=n-1; i>=1; i--) { for(y=1; y<=i; y++) { if(x[y-1]>x[y]) { temp=x[y-1]; x[y-1]=x[y]; x[y]=temp; } } } Output sorted array of Size N The worst case is the 1 st loop is executed n-1 times. The second loop is executed also n-1 times. (n-1)= n 2 -2 n+1 Which is O(n 2) 29

Bubble Sort – Analysis �Best-case: O(n) � Array is already sorted in ascending order. � The number of key comparisons: (n-1) �Worst-case: O(n) O(n 2) � Array is in reverse order: � Outer loop is executed n-1 times, � The number of key comparisons: (1+2+. . . +n-1)= n*(n-1)/2 O(n 2) �. �So, Bubble Sort is O(n 2) CENG 213 Data Structures 30

Selection Sort Algorithm Analysis 1. for fill = 0 to n-1 do 2. set pos. Min to fill for next = fill+1 to n-1 do 3. if item at next < item at pos. Min 4. set pos. Min to next 5. Exchange item at pos. Min with one at fill �In selection Sort function, the outer for loop executes n-1 times. �We invoke swap function once at each iteration. Total Swaps: n-1 Total Moves: 3*(n-1) (Each swap has three moves) 31

Selection Sort – Analysis (cont. ) �The inner for loop executes the size of the unsorted part minus 1 (from 1 to n-1), and in each iteration we make one key comparison. # of key comparisons = 1+2+. . . +n-1 = n*(n-1)/2 So, Selection sort is O(n 2) �The best case, the worst case, and the average case of the selection sort algorithm are same. all of them are O(n 2) � This means that the behavior of the selection sort algorithm does not depend on the initial organization of data. � Since O(n 2) grows so rapidly, the selection sort algorithm is appropriate only for small n. � Although the selection sort algorithm requires O(n 2) key comparisons, it only requires O(n) moves. 32

Insertion Sort analysis • for i = 2 to N do new. Element = list[ i ] location = i - 1 while (location ≥ 1) and (list[ location ] > new. Element) do list[ location + 1 ] = list[ location ] location = location - 1 end while list[ location + 1 ] = new. Element • end for 33

Insertion Sort – Analysis �Running time depends on not only the size of the array but also the contents of the array. �Best-case: O(n) � Array is already sorted in ascending order. � Inner loop will not be executed. � The number of moves: 2*(n-1) O(n) � The number of key comparisons: (n-1) O(n) �Worst-case: O(n 2) � Array is in reverse order: � Inner loop is executed i-1 times, for i = 2, 3, …, n � The number of moves: 2*(n-1)+(1+2+. . . +n-1)= 2*(n-1)+ n*(n-1)/2 � The number of key comparisons: (1+2+. . . +n-1)= n*(n-1)/2 �Average-case: O(n 2) � We have to look at all possible initial data organizations. �So, Insertion Sort is O(n 2) 34

Summary • Bubble sort, selection sort, and insertion sort are all O(n 2) • Within O(n 2), – Bubble sort is very slow, and should probably never be used for anything – Selection sort is intermediate in speed – Insertion sort is usually the fastest of the three--in fact, for small arrays (say, 10 or 15 elements), insertion sort is faster than more complicated sorting algorithms • Selection sort and insertion sort are “good enough” for small arrays 35

Quicksort – Analysis Worst Case: (assume that we are selecting the first element as pivot) � The pivot divides the list of size n into two sublists of sizes 0 and n-1. � The number of key comparisons = n-1 + n-2 +. . . + 1 = n 2/2 – n/2 O(n 2) � The number of swaps = = n-1 + n-2 +. . . + 1 swaps outside of the for loop = n 2/2 + n/2 - 1 swaps inside of the for loop O(n 2) � So, Quicksort is O(n 2) in worst case 36

Heap Sort • Build Heap Algorithm will run in O(n) time • There are n-1 calls to Heapify each call requires O(log n) time • Heap sort program combine Build Heap program and Heapify, therefore it has the running time of O(n log n) time : Ø The call to Build. Heap() takes O(n) time. Ø Each of the n - 1 calls to Heapify() takes O( lg n) time. Ø Thus the total time taken by Heapsort() = O(n) + (n - 1) O(lg n) = O(n) + O(n lg n) • Total time complexity: O(n log n) 37