Recursion and Recurrence Equations The execution of a

  • Slides: 25
Download presentation
Recursion and Recurrence Equations • The execution of a recursive program • Deriving recurrence

Recursion and Recurrence Equations • The execution of a recursive program • Deriving recurrence equations Cutler/Head

Recursion • What is the recursive definition of n! ? • Translating to Java/c

Recursion • What is the recursive definition of n! ? • Translating to Java/c int fact(int n) { if (n<=1) return 1; // Note '*' is done after returning from fact(n-1) else return n*fact(n-1); } 12/8/2020 Cutler/Head 2

Recursive algorithms • A recursive algorithm typically contains recursive calls to the same algorithm

Recursive algorithms • A recursive algorithm typically contains recursive calls to the same algorithm • In order for the recursive algorithm to terminate, it must contain code for solving directly some “base case(s)” • A direct solution does not include recursive calls. • We use the following notation: • Direct. Solution. Size is the “size” of the base case • Direct. Solution. Count is the count of the number of operations done by the “direct solution” 12/8/2020 Cutler/Head 3

A Call Tree for fact(3) The Run Time Environment • The following 2 slides

A Call Tree for fact(3) The Run Time Environment • The following 2 slides show the program stack after the third call from fact(3) • When a function is called an activation records('ar') is created and pushed on the program stack. • The activation record stores copies of local variables, pointers to other ‘ar’ in the stack and the return address. • When a function returns the stack is popped. returns 6 fact(3) 6 * 3 fact(2) 2 fact(1) * 2 1 1 int fact(int n) { if (n<=1) return 1; else return n*fact(n-1); } 12/8/2020 Cutler/Head 4

AR=Activation Record ep= environmental pointer free memory AR(fact 1) N =1 function value [=1]

AR=Activation Record ep= environmental pointer free memory AR(fact 1) N =1 function value [=1] return address static link = ep 0 dynamic link = EP free memory EP AR(fact 2) AR(fact 3) AR(Driver) N =2 function value [=? ] return address static link = ep 0 dynamic link =ep 2 N =3 function value [=? ] return address static link = ep 0 dynamic link =ep 1 AR(fact 2) N =2 function value [=2] return address static link = ep 0 dynamic link = EP ep 2 AR(fact 3) N =3 function value [=? ] return address static link = ep 0 dynamic link = ep 1 Val fact: <ip. F, ep 0> AR(Driver) ep 1 Val fact: <ip. F, ep 0> ep 0 Program stack Snapshot of the environment at end of third call to fact 12/8/2020 EP Snapshot of the environment at end of second call to fact Cutler/Head 5

free memory N =3 function value [=6] AR(fact 3) return address static link =

free memory N =3 function value [=6] AR(fact 3) return address static link = ep 0 dynamic link = EP AR(Driver) EP free memory Val AR(Driver) fact: <ip. F, ep 0> ep 0 Program stack EP Program stack Snapshot of the environment at end of first call to fact after fact l returns 12/8/2020 Cutler/Head 6

Goal: Analyzing recursive algorithms • Until now we have only analyzed (derived a count)

Goal: Analyzing recursive algorithms • Until now we have only analyzed (derived a count) for non-recursive algorithms. • In order to analyze recursive algorithms we must learn to: • Derive the recurrence equation from the code • Solve recurrence equations. 12/8/2020 Cutler/Head 7

Deriving a Recurrence Equation for a Recursive Algorithm • Our goal is to compute

Deriving a Recurrence Equation for a Recursive Algorithm • Our goal is to compute the count (Time) T(n) as a function of n, where n is the size of the problem • We will first write a recurrence equation for T(n) For example T(n)=T(n-1)+1 and T(1)=0 • Then we will solve the recurrence equation When we solve the recurrence equation above we will find that T(n)=n, and any such recursive algorithm is linear in n. Solving: Next lecture 12/8/2020 Cutler/Head 8

Deriving a Recurrence Equation for a Recursive Algorithm 1. Determine the “size of the

Deriving a Recurrence Equation for a Recursive Algorithm 1. Determine the “size of the problem”. The count T is a function of this size 2. Determine Direct. Sol. Size, such that for size Direct. Sol. Size the algorithm computes a direct solution, and the Direct. Sol. Count(s). 12/8/2020 Cutler/Head 9

Deriving a Recurrence Equation for a Recursive Algorithm To determine General. Count: 3. Identify

Deriving a Recurrence Equation for a Recursive Algorithm To determine General. Count: 3. Identify all the recursive calls done by a single call of the algorithm and their counts, T(n 1), …, T(nk) and compute Recursive. Call. Sum = 4. Determine the “non recursive count” t(size) done by a single call of the algorithm, i. e. , the amount of work, excluding the recursive calls done by the algorithm 12/8/2020 Cutler/Head 10

Deriving Direct. Solution. Count for Factorial int fact(int n) { if (n<=1) return 1;

Deriving Direct. Solution. Count for Factorial int fact(int n) { if (n<=1) return 1; // Note '*' is done after returning from fact(n-1) else return n*fact(n-1); 1. Size = n 2. Direct. Sol. Size is (n<=1) 3. Direct. Sol. Count is (1) The algorithm does a small constant number of operations (comparing n to 1, and returning) 12/8/2020 Cutler/Head 11

Deriving a General. Count for Factorial int fact(int n) { if (n<=1) return 1;

Deriving a General. Count for Factorial int fact(int n) { if (n<=1) return 1; // Note '*' is done after returning from fact(n-1) Operations else counted in return n * fact(n-1); The only recursive t(n) call, requiring T(n - 1) operations 3. Recursive. Call. Sum = T( n - 1) 4. t(n) = (1) 12/8/2020 (for if, *, -, return) Cutler/Head 12

Deriving a Recurrence Equation for Mystery In this example we are not concerned with

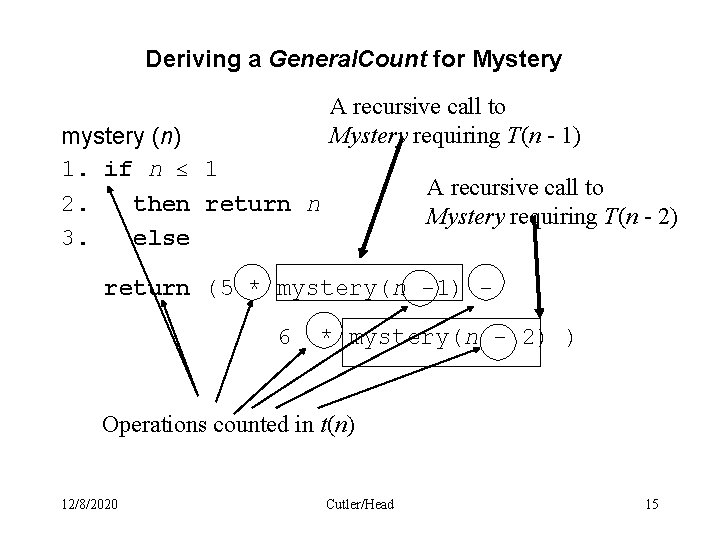
Deriving a Recurrence Equation for Mystery In this example we are not concerned with what mystery computes. Our goal is to simply write the recurrence equation mystery (n) 1. if n 1 2. then return n 3. else return (5 * mystery(n -1) 6* mystery(n -2) ) 12/8/2020 Cutler/Head 13

Deriving a Direct. Solution. Count for Mystery 1. Size = n Direct. Sol. Size

Deriving a Direct. Solution. Count for Mystery 1. Size = n Direct. Sol. Size is (n<=1) 3. Direct. Sol. Count is (1) The algorithm does a small constant number of operations (comparing n to 1, and returning) 2. 12/8/2020 Cutler/Head 14

Deriving a General. Count for Mystery mystery (n) 1. if n 1 2. then

Deriving a General. Count for Mystery mystery (n) 1. if n 1 2. then return n 3. else A recursive call to Mystery requiring T(n - 1) A recursive call to Mystery requiring T(n - 2) return (5 * mystery(n -1) 6 * mystery(n - 2) ) Operations counted in t(n) 12/8/2020 Cutler/Head 15

Deriving a Recurrence Equation for Mystery 3. Recursive. Call. Sum = T(n-1) + T(n-2)

Deriving a Recurrence Equation for Mystery 3. Recursive. Call. Sum = T(n-1) + T(n-2) 4. t (n)= (1) The non recursive count includes the comparison n<=1, the 2 multiplications, the subtraction, and the return. So (1). 12/8/2020 Cutler/Head 16

Deriving a Recurrence Equation for Multiply(y, z)//binary multiplication 1. if (z ==0) return 0

Deriving a Recurrence Equation for Multiply(y, z)//binary multiplication 1. if (z ==0) return 0 2. else if z is odd 3. then return (multiply(2 y, z/2 ) + 4. else return (multiply(2 y, z/2 )) Barometer operation y) To derive the recurrence equation we need to determine the size of the problem. The variable which is decreased and provides the direct solution is z. So we can use z as the size. Another possibility is to use n which is the number of bits in z (n= lg z +1). Let addition be our barometer operation. We do 0 additions for the direct solution. So Direct. Solution. Size =0, and Direct. Solution. Count=0 12/8/2020 Cutler/Head 17

Deriving a Recurrence Equation for Multiply 1. Recursive. Call. Sum = T(z/2) t(z) =

Deriving a Recurrence Equation for Multiply 1. Recursive. Call. Sum = T(z/2) t(z) = 1 addition in the worst case. So Solving this equation we get T(z)= (lg z)= (n). 2. Recursive. Call. Sum = T(n-1) since z/2 has n-1 bits Solving this equation we get T(n)= (n) 12/8/2020 Cutler/Head 18

Deriving a recurrence equation for minimum Minimum(A, lt, rt) // minimum(A, 1, length(A)) 1.

Deriving a recurrence equation for minimum Minimum(A, lt, rt) // minimum(A, 1, length(A)) 1. if rt - lt 1 2. then return (min(A[lt], A[rt])) 3. else m 1 = minimum(A, lt, (lt+rt)/2 ) 4. m 2 = minimum(A, (lt+rt)/2 +1, rt) 5. return (min (m 1, m 2)) • This procedure computes the minimum of the left half of the array, the right half of the array, and the minimum of the two. • Size = rt-lt+1= n • Direct. Solution. Size is n = (rt - lt)+1 1+1=2. • Direct. Solution. Count = (1) 12/8/2020 Cutler/Head 19

Deriving a recurrence equation for minimum Minimum(A, lt, rt) // minimum(A, 1, length(A)) 1.

Deriving a recurrence equation for minimum Minimum(A, lt, rt) // minimum(A, 1, length(A)) 1. if rt - lt 1 2. then return (min(A[lt], A[rt])) 3. else m 1 = minimum(A, lt, (lt+rt)/2 ) 4. 5. m 2 = minimum(A, (lt+rt)/2 +1, rt) return (min (m 1, m 2)) Two recursive calls with n/2 elements. So T(n/2) + T(n/2) 12/8/2020 Cutler/Head 20

Deriving a recurrence equation for Merge Sort: 1 if (n 2) 2 move. First(

Deriving a recurrence equation for Merge Sort: 1 if (n 2) 2 move. First( S, S 1, (n+1)/2)) // divide 3 move. Second( S, S 2, n/2) // divide 4 Sort(S 1) // recurs 5 Sort(S 2) // recurs 6 Merge( S 1, S 2, S ) // conquers Direct. Solution. Size is n<2 Direct. Solution. Count is (1) Recursive. Call. Sum is T( n/2 ) + T( n/2 ) The non recursive count t(n) = (n) 12/8/2020 Cutler/Head 21

Recurrence Equation for cost. • The implementation of the moves costs Q(n) and the

Recurrence Equation for cost. • The implementation of the moves costs Q(n) and the merge costs Q(n). So the total cost for dividing and merging is Q(n). • The recurrence relation for the run time of Sort is T(n) = T( n/2 ) + Q(n). T(0) =T(1) = Q(1) • The solution is T(n)= Q(nlg n) 12/8/2020 Cutler/Head 22

Computing xn • We can decrease the number of times that x is multiplied

Computing xn • We can decrease the number of times that x is multiplied by itself by observing that to compute x 8 we need only 3 multiplications (x 2=x*x, x 4=x 2*x 2, and x 8=x 4*x 4) and when we want of compute x 9, we need 4 multiplications (x 2=x*x, x 4=x 2*x 2, x 8=x 4*x 4 and x 9= x 8*x) • A recursive procedure for computing xn should be (lg n) • For the following algorithm we will derive the worst case recurrence equation. • Note: we are ignoring the fact that the numbers will quickly become too large to store in a long integer 12/8/2020 Cutler/Head 23

Recursion - Power long power (long x, long n) { if (n == 0)

Recursion - Power long power (long x, long n) { if (n == 0) { return 1; } else { long p = power(x, n/2); if ((n % 2) == 0) { return p*p; } else { return x * p*p; } } } We use the * as our barometer operation. 12/8/2020 Cutler/Head 24

Deriving a Recurrence Equation for Power Size = n Direct. Solution. Size is n=0;

Deriving a Recurrence Equation for Power Size = n Direct. Solution. Size is n=0; Direct. Solution. Count is 0; Recursive. Call. Sum is T(n/2) // t(n) = 2 multiplications in the worst case T(n)=0 for n=0 T(n)=T(n/2)+2 for n>0 12/8/2020 Cutler/Head 25

Recurrence Relations Recurrence Relations A recurrence relation isRecurrence Relations Recurrence Relations A recurrence relation is
Recursion Recursion Slide 2 Recursion Recursion Slide 3Recursion Recursion Slide 2 Recursion Recursion Slide 3
Recursion and Induction Themes Recursion Recursive Definitions RecurrenceRecursion and Induction Themes Recursion Recursive Definitions Recurrence
Recursion and Induction Themes Recursion Recursive Definitions RecurrenceRecursion and Induction Themes Recursion Recursive Definitions Recurrence
Recursion and Induction Themes Recursion Recurrence Relations RecursiveRecursion and Induction Themes Recursion Recurrence Relations Recursive
Recursion and Induction Themes Recursion Recurrence Definitions RecursiveRecursion and Induction Themes Recursion Recurrence Definitions Recursive
Recursion and Induction Themes Recursion Recurrence Definitions RecursiveRecursion and Induction Themes Recursion Recurrence Definitions Recursive
Data Structures LECTURE 3 Recurrence equations Formulating recurrenceData Structures LECTURE 3 Recurrence equations Formulating recurrence
Solving recurrence equations 5 techniques for solving recurrenceSolving recurrence equations 5 techniques for solving recurrence
Recursion CMSC 201 Recursion Vs Iteration Recursion andRecursion CMSC 201 Recursion Vs Iteration Recursion and
Recursion CMSC 201 Recursion Vs Iteration Recursion andRecursion CMSC 201 Recursion Vs Iteration Recursion and
Recursion CMSC 201 Recursion Vs Iteration Recursion andRecursion CMSC 201 Recursion Vs Iteration Recursion and
Recursion CMSC 201 Recursion Vs Iteration Recursion andRecursion CMSC 201 Recursion Vs Iteration Recursion and
Chapter 11 Recursion Recursion Recursion is a fundamentalChapter 11 Recursion Recursion Recursion is a fundamental
Chapter 11 Recursion Recursion Recursion is a fundamentalChapter 11 Recursion Recursion Recursion is a fundamental
Programming with Recursion Using Recursion 1 The RecursionProgramming with Recursion Using Recursion 1 The Recursion
Recursion Recursion What is recursion When one functionRecursion Recursion What is recursion When one function
Recursion in Java recursion Recursion is the processRecursion in Java recursion Recursion is the process
Extra Practice for Recursion Recursion l Recursion isExtra Practice for Recursion Recursion l Recursion is
Building Java Programs Chapter 12 Recursion Recursion recursionBuilding Java Programs Chapter 12 Recursion Recursion recursion
Recursion Recursion Recursion is the name given forRecursion Recursion Recursion is the name given for
Tail Recursion Problems with Recursion Recursion is generallyTail Recursion Problems with Recursion Recursion is generally
Tail Recursion Problems with Recursion Recursion is generallyTail Recursion Problems with Recursion Recursion is generally
Recursion Examples Recursion review Recursion review Scenario YouRecursion Examples Recursion review Recursion review Scenario You