COMP 319 Algorithm Analysis Franklin University Module 1

COMP 319 Algorithm Analysis Franklin University Module 1: Overview of Algorithms Week 2 Jay N. Bhuyan 1

COMP 319 Algorithm Analysis Franklin University Searching 1. Sequential Search on an unsorted table of records. 2. Searches on an ordered (sorted) table of records: • Ordered linear search • Binary search 2

COMP 319 Algorithm Analysis Franklin University Recursive Binary search index location (index low, index high){ index mid; if (low > high) return 0; else { mid = (low + high)/2 ; if ( x == S[mid]) return mid; else if (x < S[mid]) return location(low, mid-1); else return location(mid+1, high); } } 3

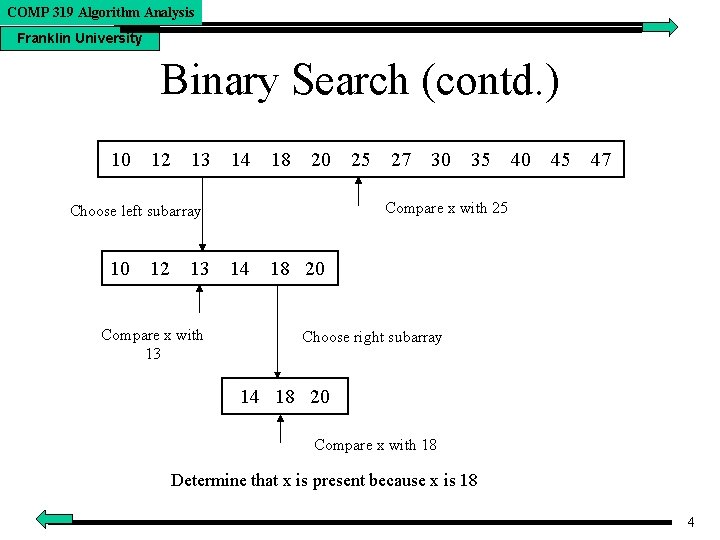
COMP 319 Algorithm Analysis Franklin University Binary Search (contd. ) 10 12 13 14 18 20 27 30 35 40 45 47 Compare x with 25 Choose left subarray 10 12 13 14 Compare x with 13 25 18 20 Choose right subarray 14 18 20 Compare x with 18 Determine that x is present because x is 18 4

COMP 319 Algorithm Analysis Franklin University Binary Search (contd. ) Time Complexity of Binary Search algorithm W(n) = W (n/2) + 1 for n>1, n a power of 2 W(1) = 1 The solution: W(n) = lg n + 1 If n is not restricted to be a power of 2, then W(n) = lg n + 1 (lg n). 5

COMP 319 Algorithm Analysis Franklin University Searching (contd. ) A possible improvement in binary search is not to use the middle element at each step, but to guess more precisely where the key being sought falls within the current interval of interest. Some of such searches are: • Variations on a binary search, e. g. , an interpolation search • Fibonacci search Instead of splitting the array in the middle, this implementation splits the array corresponding to the fibonacci numbers, which are defined as follows: F 0 = 0, F 1 = 1 Fn = Fn-1+Fn-2 for n>=2. • Indexed sequential search • Binary tree search 6

COMP 319 Algorithm Analysis Franklin University • • Searching (contd. ): Hashing Unlike other searches, not based on comparison of keys. therefore improved performance Ex: System software. Uses hash tables to store records. Key, or a portion of key, is used to point to associated record placed in hash table. Examine key and know where to look in the table based on this examination. In static hashing, we store the records in a fixed size hash table. Hash table is stored in sequential memory locations that are partitioned into buckets, 0 to (b-1). The hash function, f(x), maps the set of possible keys onto the integers, 0 to (b-1). Typically, each bucket in the hash table can hold one record, but each bucket could be further divided into a number of slots (for instance, 2 slots per bucket). 7

COMP 319 Algorithm Analysis Franklin University Hashing (contd. ) • The loading factor or loading density of the hash table is given by the formula: lf = n /(s*b) where n = the number of records in the table, b = the number of buckets in the table, and s = the number of slots per bucket. • Two keys, i 1 and i 2, are called synonyms with respect to the hash function, f, if f(i 1) = f(i 2). • We can enter distinct synonyms into the same bucket as long as slots are available. A collision occurs when we hash two distinct (non-identical) keys into the same bucket, and an overflow situation occurs when we hash a new key into a full bucket. When there is only one slot per bucket, then every collision causes an overflow to occur. 8

COMP 319 Algorithm Analysis Franklin University Hashing (contd. ) Hash Function: • Minimize the number of collisions and make it easy to compute. – To avoid collisions, the hash function should depend on all characters in a key and should also be unbiased, i. e. , a random x should have an equal chance of hashing into any of the b buckets in the hash table. Uniform Hash Functions are hash functions that satisfy these properties. 9

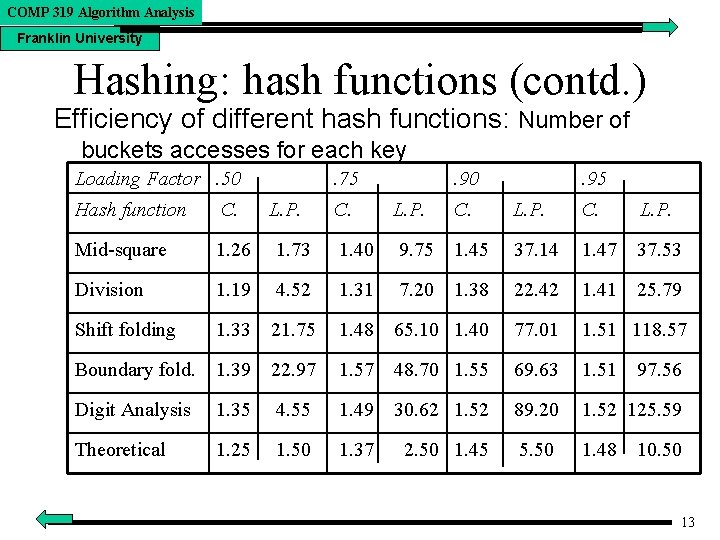
COMP 319 Algorithm Analysis Franklin University Hashing: hash functions (contd. ) 1. Mid-square hash function. • • Frequently used in symbol table applications Squaring a numeric equivalent to the key Using an appropriate number of bits from the middle of the square to obtain the bucket address The size of the hash table should always be a power of 2 for this method. 10

COMP 319 Algorithm Analysis Franklin University Hashing: hash functions (contd. ) 2. Division hash function. f(x) = x%m, where m represents the table size. This would then generate the bucket addresses, 0 to (m-1). 3. Folding hash function. This method involves partitioning the key into several parts. All parts, except the last one, should be of the same length. Shift Folding: The parts are then added together to form the bucket address in the hash table. Ex: x(12320324111220) into the following parts: x 1 = 123 x 2 = 203 x 3= 241 x 4 = 112 x 5 = 20 Address = 699 11

COMP 319 Algorithm Analysis Franklin University Hashing(contd. ) Boundary Folding: Reverses every other partition before adding Methods for handling overflow: • • Chaining Uses a hash table that is an array or vector of linked list Linear Probing A linear search of the table begins at the location where collision occurs and continues until an empty slot is found in which the item can be stored. 12

COMP 319 Algorithm Analysis Franklin University Hashing: hash functions (contd. ) Efficiency of different hash functions: Number of buckets accesses for each key Loading Factor. 50 . 75 Hash function C. L. P. C. Mid-square 1. 26 1. 73 1. 40 Division 1. 19 4. 52 Shift folding 1. 33 . 90 L. P. . 95 C. L. P. 9. 75 1. 45 37. 14 1. 47 37. 53 1. 31 7. 20 1. 38 22. 42 1. 41 25. 79 21. 75 1. 48 65. 10 1. 40 77. 01 1. 51 118. 57 Boundary fold. 1. 39 22. 97 1. 57 48. 70 1. 55 69. 63 1. 51 Digit Analysis 1. 35 4. 55 1. 49 30. 62 1. 52 89. 20 1. 52 125. 59 Theoretical 1. 25 1. 50 1. 37 2. 50 1. 45 5. 50 1. 48 97. 56 10. 50 13

COMP 319 Algorithm Analysis Franklin University Hashing: Example • Suppose that following character codes are used: ‘A’=1, ‘B’=2, …, ‘Y’=25, ‘Z’=26. Using a hash table with 11 locations and the hashing function h(identifier) = average%11, where average is the average of first and the last letters in identifier. • Show the hash table that results when the following identifiers are inserted in the order given, assuming that collisions are resolved using linear probing: • BETA, RATE, FREQ, MEAN, SUM, NUM, BAR, WAGE, PAY, KAPPA. 14

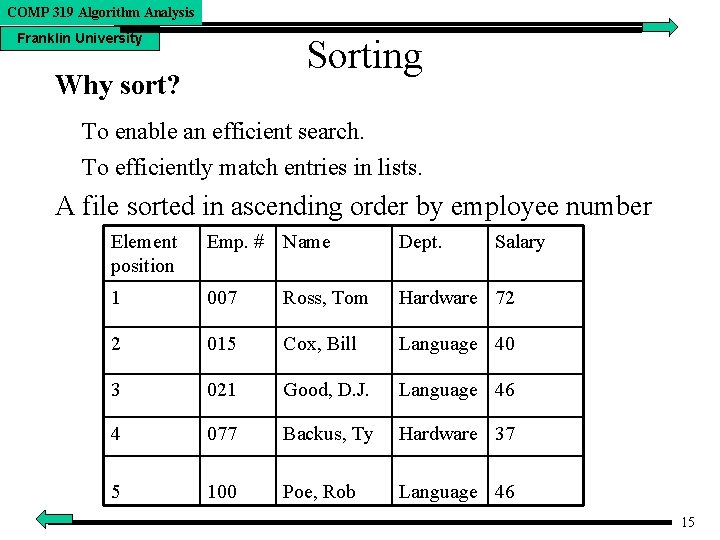
COMP 319 Algorithm Analysis Franklin University Sorting Why sort? To enable an efficient search. To efficiently match entries in lists. A file sorted in ascending order by employee number Element position Emp. # Name Dept. Salary 1 007 Ross, Tom Hardware 72 2 015 Cox, Bill Language 40 3 021 Good, D. J. Language 46 4 077 Backus, Ty Hardware 37 5 100 Poe, Rob Language 46 15

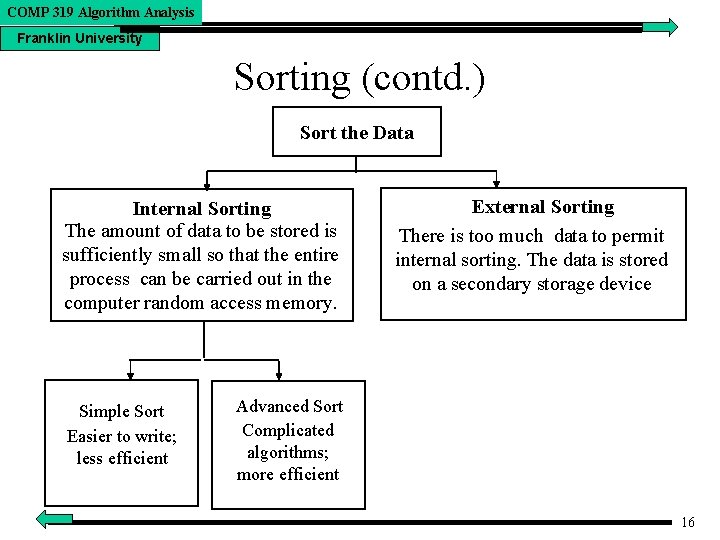
COMP 319 Algorithm Analysis Franklin University Sorting (contd. ) Sort the Data Internal Sorting The amount of data to be stored is sufficiently small so that the entire process can be carried out in the computer random access memory. Simple Sort Easier to write; less efficient External Sorting There is too much data to permit internal sorting. The data is stored on a secondary storage device Advanced Sort Complicated algorithms; more efficient 16

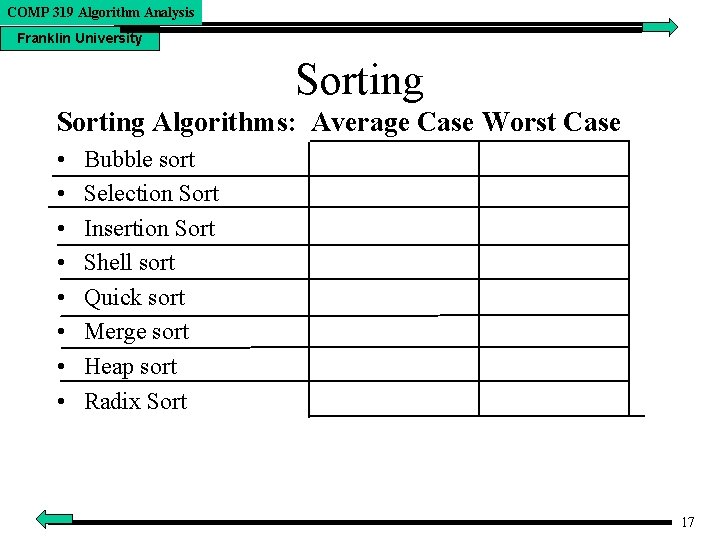
COMP 319 Algorithm Analysis Franklin University Sorting Algorithms: Average Case Worst Case • • Bubble sort Selection Sort Insertion Sort Shell sort Quick sort Merge sort Heap sort Radix Sort 17

COMP 319 Algorithm Analysis Franklin University Sorting void Selection. Sort (Type a[], int n) Step # Step Count { (Best Case) for (int i=1; i<=n; i++) ----- (1) + n+1 { int j = i; ----- (2) +n for (int k =i+1; k<=n; k++) ---(3) + (n(n+1))/2 if (a[k]<a[j]) ----- (4) + (n(n-1))/2 j=k; ----- (5) +0 Type t = a[i]; ----- (6) +n a[i] = a[j]; ----- (7) +n a[j] = t; ----- (8) +n } } Total Count: (2 n 2+10 n+2)/2 Order of Complexity: (n 2) Step Count (Worst Case) + n+1 +n + (n(n+1))/2 + (n(n-1))/2 +n +n +n (3 n 2+9 n+2)/2 (n 2) 18

COMP 319 Algorithm Analysis Franklin University Exchange Sort: Sorting void exchangesort (int n, keytype S[]) { index i, j; for (i=1; i<= n-1; i++) for (j = i+1; j <=n; j++) if (S[i] < S[j]) exchange S[i] and S[j]; } • Time Complexity? 19

COMP 319 Algorithm Analysis Franklin University Sorting (Contd. ) Insertion Sort: void insertionsort (int n, keytypes[]) { index i, j; keytype x; for ( i = 2; i <=n; i++) { x = s[i]; j = i-1; while (j > 0 && s[j] > x) { s[j+1] = s[j]; j--; } s[ j + 1] = x; } Time Complexity? 20

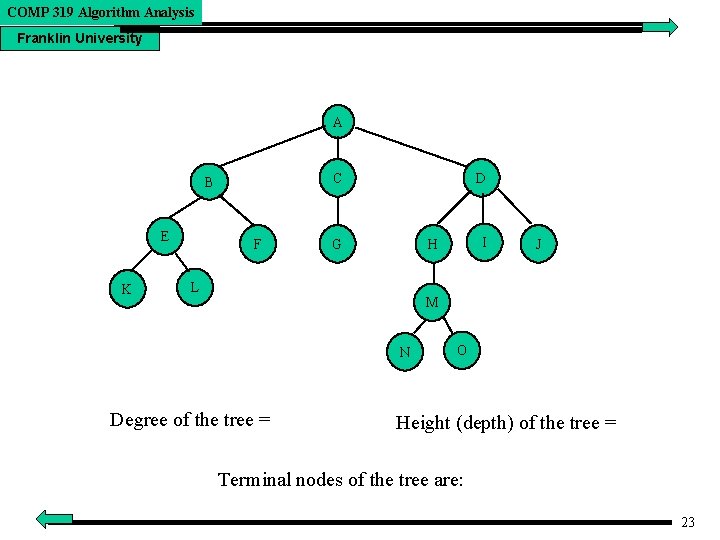
COMP 319 Algorithm Analysis Franklin University Trees • Definition: A tree (which is one type of a data structure) is a finite set of one or more nodes such that: There is a specially designated node called root. The remaining nodes are divided into n>=0 disjoint sets T 1, T 2, . . . Tn where each of these sets is a tree. T 1, T 2, . . Tn are called the subtrees of the root. • • • Node - represents an item of information stored in the tree. Branches - represent the links between the nodes. Root of the tree or root node - node at the top of the tree, the start of the tree. Degree of a node - the number of subtrees of the node (i. e. , the number of children from any one node). Degree of a tree - the maximum degree of any of the nodes in the tree. Leaf or terminal nodes - nodes with degree 0. • • • 21

COMP 319 Algorithm Analysis Franklin University Tree Terminology (contd. ) 7. 8. 9. 10. 11. 12. Child/children - the roots of the subtrees of the parent node. Siblings - children of the same parent. Parent - a node that has subtrees (i. e. , a node that has children). Level of a node - defined by root = 1, children of root = 2, grandchildren of root = 3, etc. (In some textbooks, the root is defined to be at level 0, children of the root at level 1, etc. ) Depth or height of a tree - the maximum level of any node in the tree. Binary trees are trees with no more than two-way branching from each node in the tree. A binary tree is either empty or consists of a root node and two disjoint binary trees called left and right subtrees. 22

COMP 319 Algorithm Analysis Franklin University A C B E K F D G I H L J M N Degree of the tree = O Height (depth) of the tree = Terminal nodes of the tree are: 23

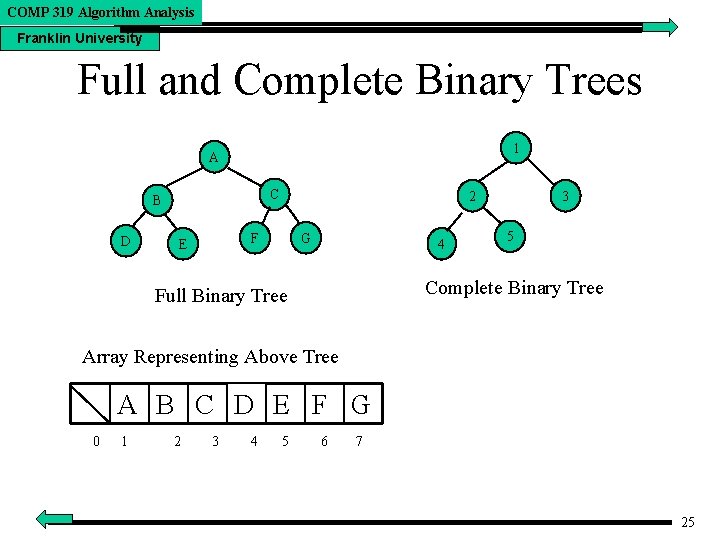
COMP 319 Algorithm Analysis Franklin University Binary Trees: Properties • The maximum number of nodes on level i of a binary tree is 2 (i-1) , where i >= 1. • The maximum number of nodes in a binary tree of depth k is 2 k - 1, where k >= 1. • For any non-empty binary tree, T, if n 0 represents the number of leaf nodes and n 2 represents the number of nodes with degree 2, then n 0 = n 2 + 1. • A full binary tree of depth k is a binary tree of depth k having 2 k - 1 nodes, where k >= 1. • A binary tree with n nodes and depth k is complete if and only if its nodes correspond to the nodes numbered from 1 to n in the full binary tree of depth k, filling in from left to right on each level. 24

COMP 319 Algorithm Analysis Franklin University Full and Complete Binary Trees 1 A C B D 2 F E G 4 3 5 Complete Binary Tree Full Binary Tree Array Representing Above Tree A B C D E F G 0 1 2 3 4 5 6 7 25

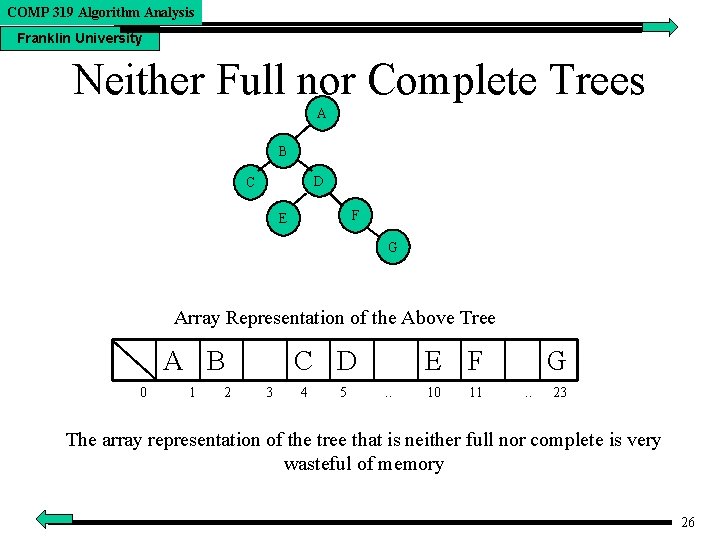
COMP 319 Algorithm Analysis Franklin University Neither Full nor Complete Trees A B D C F E G Array Representation of the Above Tree A B 0 1 2 C D 3 4 5 E F. . 10 11 G. . 23 The array representation of the tree that is neither full nor complete is very wasteful of memory 26

COMP 319 Algorithm Analysis Franklin University Sorting Algorithms (contd. ) Heapsort A heap is a complete binary tree such that the value of the key in the root is greater than the value of the key in each of its children, and that both subtrees are also heaps (a recursive definition). Heapsort: (1) Make a heap of the elements to be sorted (the siftup process). (2) Convert the heap into a sorted list (the sift-down process) 10 6 9 3 2 5 27

COMP 319 Algorithm Analysis Franklin University Sorting Algorithms (contd. ) Radix Sort • Sorting algorithm that is not based on comparison of keys. To sort the following list of numbers: 64, 8, 216, 512, 27, 729, 0, 1, 343, 125. • Radix sort requires that we know something about the data being sorted. • Numbers are decimal numbers so use 10 buckets (radix). • Numbers fall in the range: 0 to 999. Therefore, we will require 3 passes to complete the sort. 28

COMP 319 Algorithm Analysis Franklin University Radix Sort (contd. ) Pass 1: place the numbers to be sorted into the location that represents the least significant digit of the number. 0 1 2 3 4 5 6 7 8 9 0 1 512 343 64 125 216 27 8 729 Pass 2: place the numbers taken from pass 1 into the location that represents the middle digit of each number. 0 8 1 0. 1 2 216 512 729 27 125 3 4 343 5 6 7 8 9 64 29

COMP 319 Algorithm Analysis Franklin University Radix Sort (contd. ) Pass 3: place the number taken from pass 2 into the location that represents the most significant digit of each number. 0 1 64 27 8 1 0 2 3 125 216 343 4 5 512 6 7 8 9 729 The numbers are then read from their locations to produce the sorted list. 30

COMP 319 Algorithm Analysis Franklin University Radix Sort (contd. ) Order of complexity of Radix Sort algorithm: O(max_digits(radix_size + n)) where max_digits = the number of passes needed by the sort (the number of digits in the key) radix_size = the size of the radix n = the number of elements to be sorted 31