CMSC 335 COMPUTER GRAPHICS LECTURE 6 2 D







































- Slides: 51

CMSC 335 COMPUTER GRAPHICS LECTURE 6 • • 2 D TRANSFORMATIONS • VIEWING TRANSFORMATIONS 3 D TRANSFORMATIONS

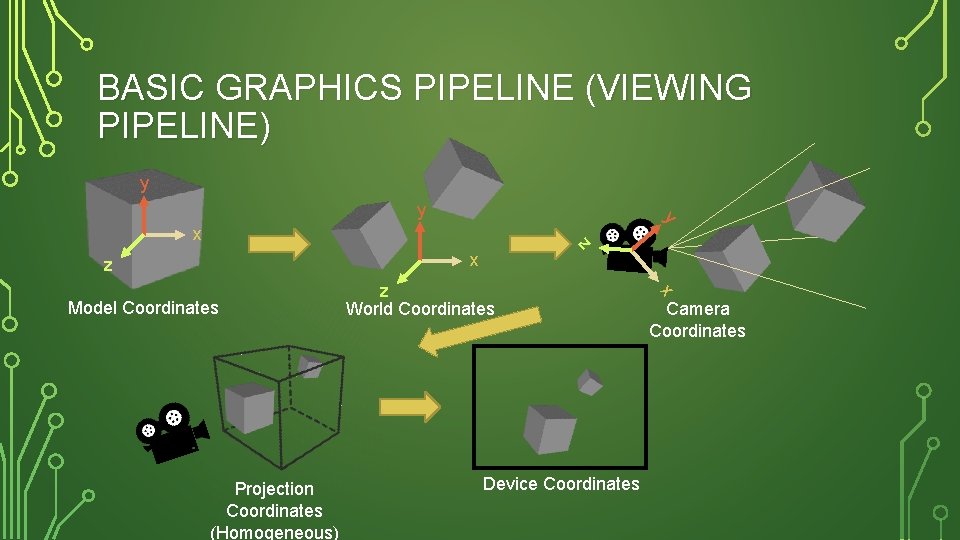
BASIC GRAPHICS PIPELINE (VIEWING PIPELINE) y y y z x x z Projection Coordinates (Homogeneous) Device Coordinates x Model Coordinates z World Coordinates Camera Coordinates

2 D TRANSFORMATIONS

TRANSLATION FIRST LOOK • How would you apply this to a whole shape? What if shape is defined like a circle?

LINEAR TRANSFORMATIONS •

SCALING • How would you apply this to a whole shape? What if shape is defined like a circle?

SHEARING • Can be thought of as rotating one axis only. How would you apply this to a whole shape? What if shape is defined like a circle?

ROTATION •

ROTATION •

ROTATION • How would you apply this to a whole shape? What if shape is defined like a circle?

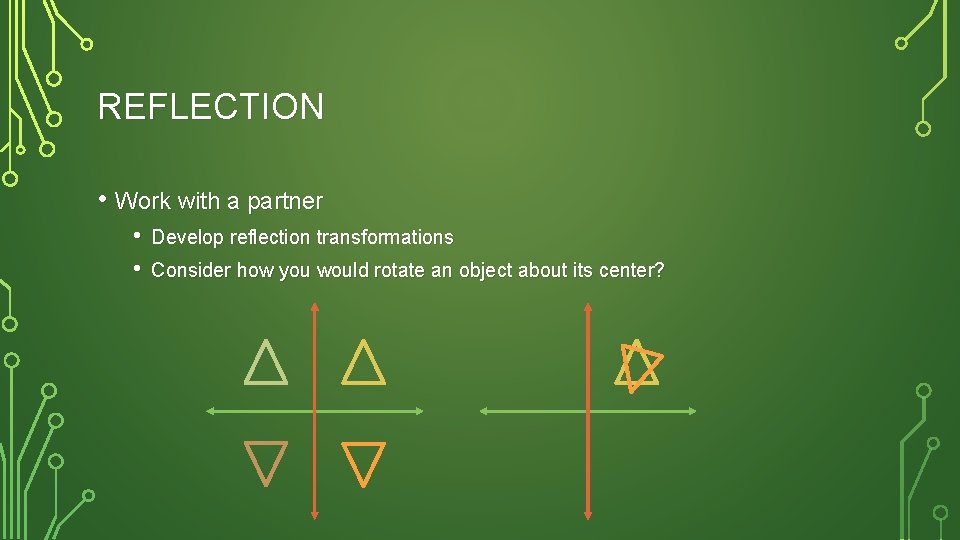
REFLECTION • Work with a partner • • Develop reflection transformations Consider how you would rotate an object about its center?

COMPOSING TRANSFORMATIONS •

COMPOSING TRANSFORMATIONS • This extrapolates to as many sequential operations as we want! • So we should compose a matrix of all of our transformations on an object first, and then apply it to an object. • Why? • • Does order matter? • • Argue with a comparison to a brute force algorithm and big-oh complexity. Determine a concrete example Can you compose all transformation types in this way? • Explain why/why not?

COMPOSING TRANSFORMATIONS •

FIXING TRANSLATIONS •

TRANSLATIONS WITH HOMOGENEOUS COORDINATES •

ADJUSTED SCALE • Synonymous Modification for Shearing/Reflection

ADJUSTED ROTATION •

HIERARCHICAL SYSTEMS • Consider the following: • • • A robot arm A dog walking A solar system • What is in common about animating them? • • All have many individual pieces Placement of the pieces depends on each other

HIERARCHICAL SYSTEMS • Z Y X W

3 D TRANSFORMATIONS

BASICS • Everything is synonymous • We will use a 4 D homogeneous coordinate so that translations can be represented as a linear transformation • • Rotations have 3 separate matrices (for now)… Linear transformations are composed the same and have the same ordering limitations • Create a composite matrix to apply to each point

TRANSLATION •

SCALING • Synonymous Modification for Shearing/Reflection

ROTATIONS •

A NOTE ON 3 D ROTATIONS •

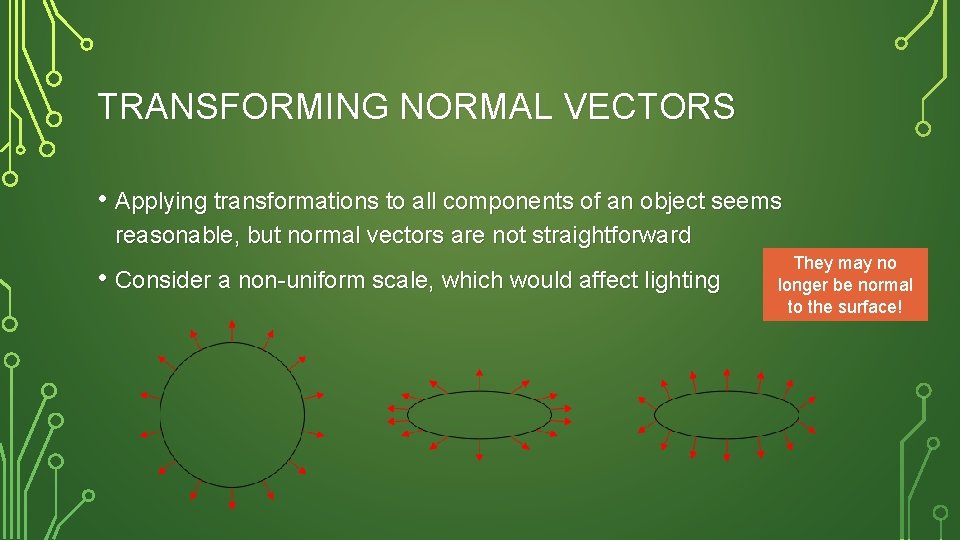
TRANSFORMING NORMAL VECTORS • Applying transformations to all components of an object seems reasonable, but normal vectors are not straightforward • Consider a non-uniform scale, which would affect lighting They may no longer be normal to the surface!

TRANSFORMING NORMAL VECTORS •

INVERSE TRANSFORMATIONS •

COORDINATE TRANSFORMATIONS •

VIEWING TRANSFORMATIONS

VIEWING TRANSFORMATION • So far, our transformations have been between 3 D transformations in the world • We now need viewing transformations that map from 3 D to 2 D

RECALL OUR VIEWING TYPES • Parallel (Orthographic) • Parallel lines, stay parallel • Perspective • Parallel lines converge at vanishing points

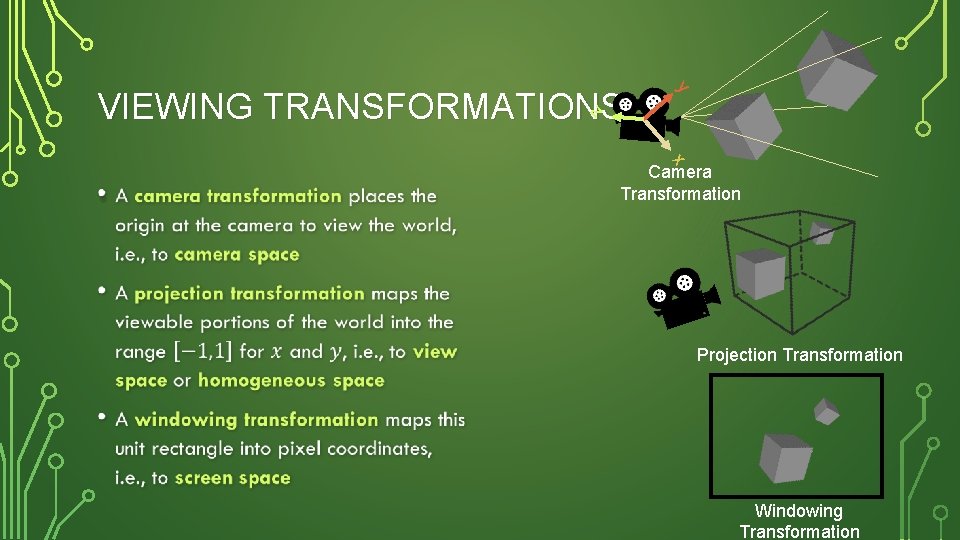
y z VIEWING TRANSFORMATIONS x • Camera Transformation Projection Transformation Windowing Transformation

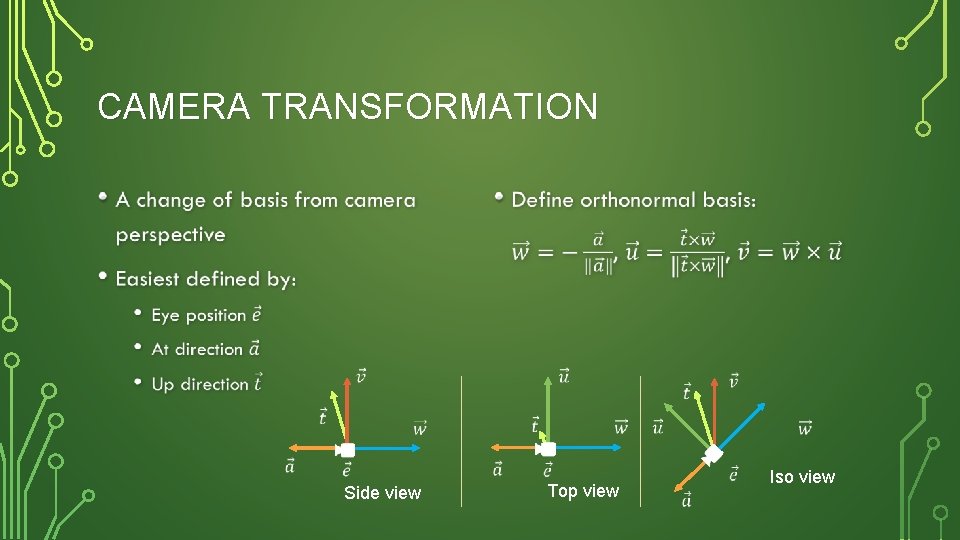
CAMERA TRANSFORMATION • • Side view Top view Iso view

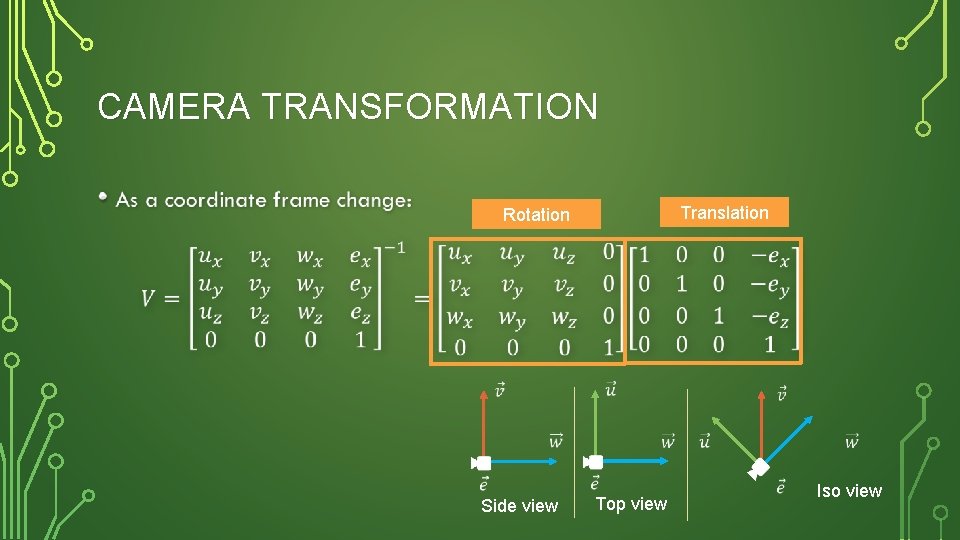
CAMERA TRANSFORMATION • Translation Rotation Side view Top view Iso view

CAMERA TRANSFORMATION • Iso view

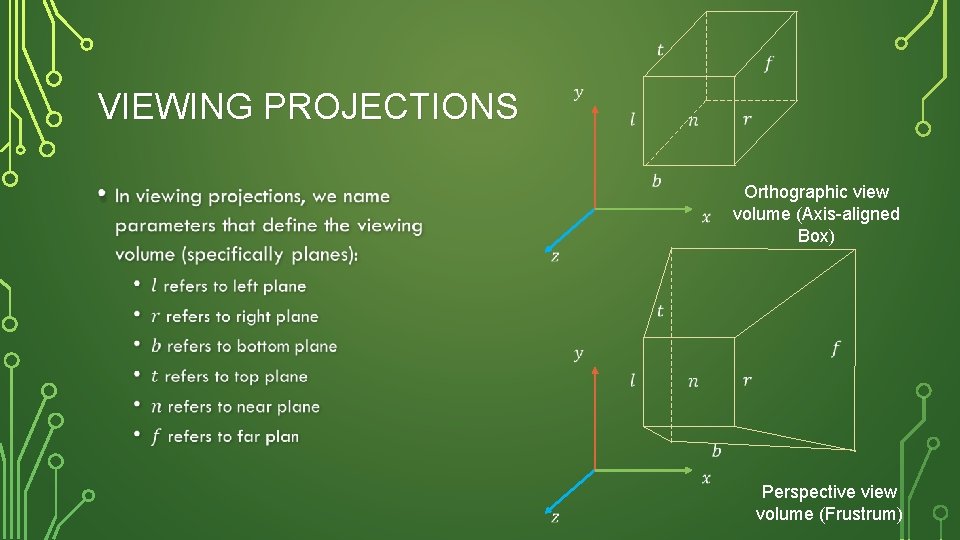
VIEWING PROJECTIONS • Orthographic view volume (Axis-aligned Box) Perspective view volume (Frustrum)

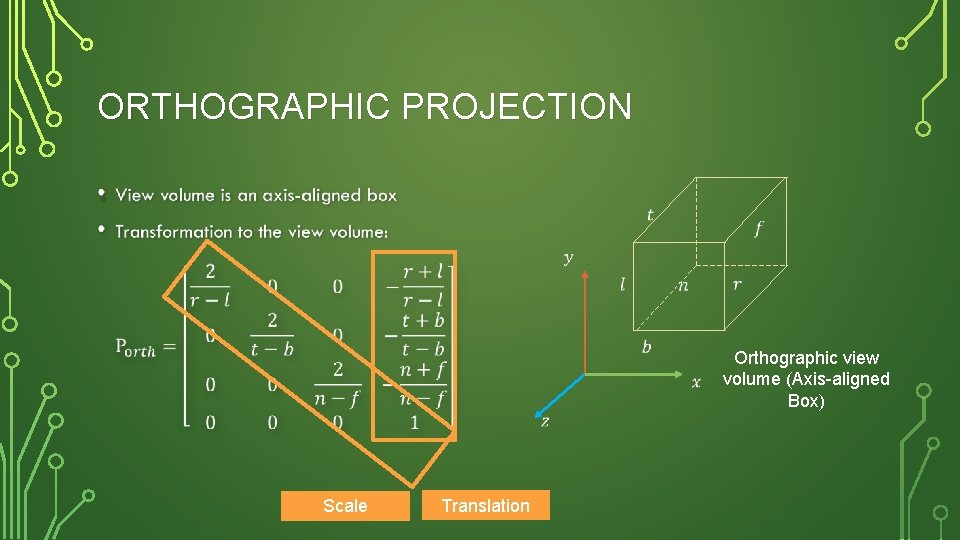
ORTHOGRAPHIC PROJECTION • Orthographic view volume (Axis-aligned Box) Scale Translation

ORTHOGRAPHIC PROJECTION • Easy method that returns the matrix • glm: : ortho(l, r, b, t, n, f) • Or • glm: : ortho(l, • a 2 Dish version… r, b, t) Orthographic view volume (Axis-aligned Box)

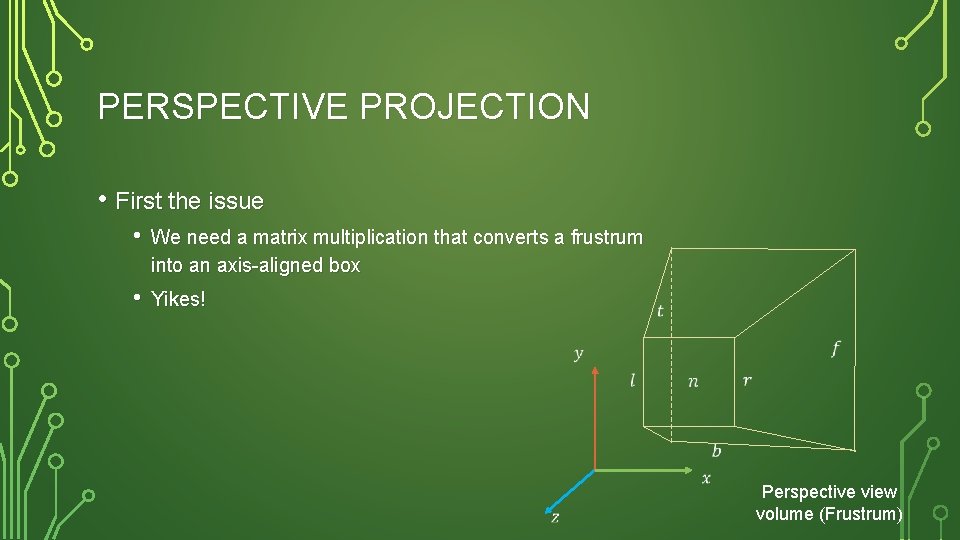
PERSPECTIVE PROJECTION • First the issue • We need a matrix multiplication that converts a frustrum into an axis-aligned box • Yikes! Perspective view volume (Frustrum)

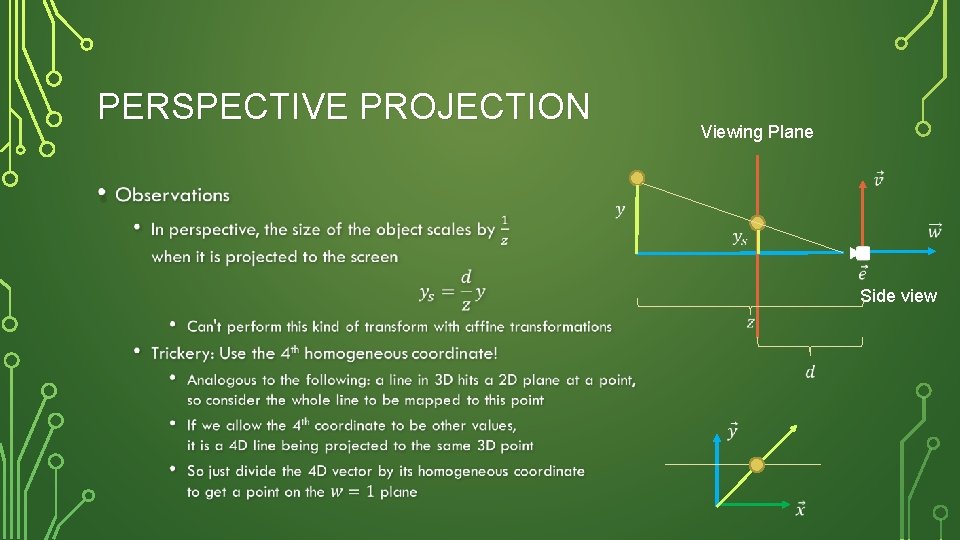
PERSPECTIVE PROJECTION Viewing Plane • Side view

PERSPECTIVE PROJECTION •

PERSPECTIVE PROJECTION •

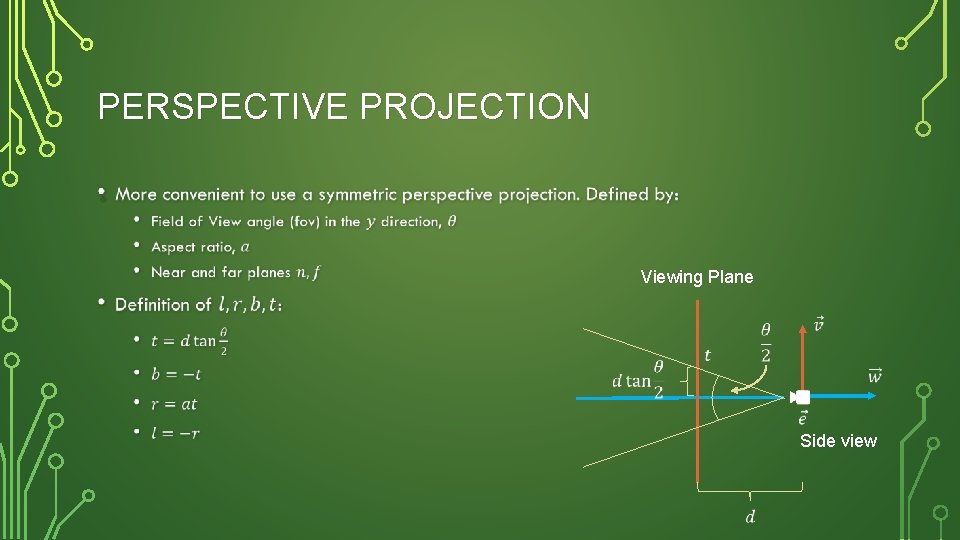
PERSPECTIVE PROJECTION • Viewing Plane Side view

PERSPECTIVE PROJECTION • Both perspective and symmetric perspective are easily acquired in glm • glm: : frustrum(l, r, b, t, n, f) • Generalized perspective • glm: : perspective(fovy, • Symmetric perspective aspect, n, f)

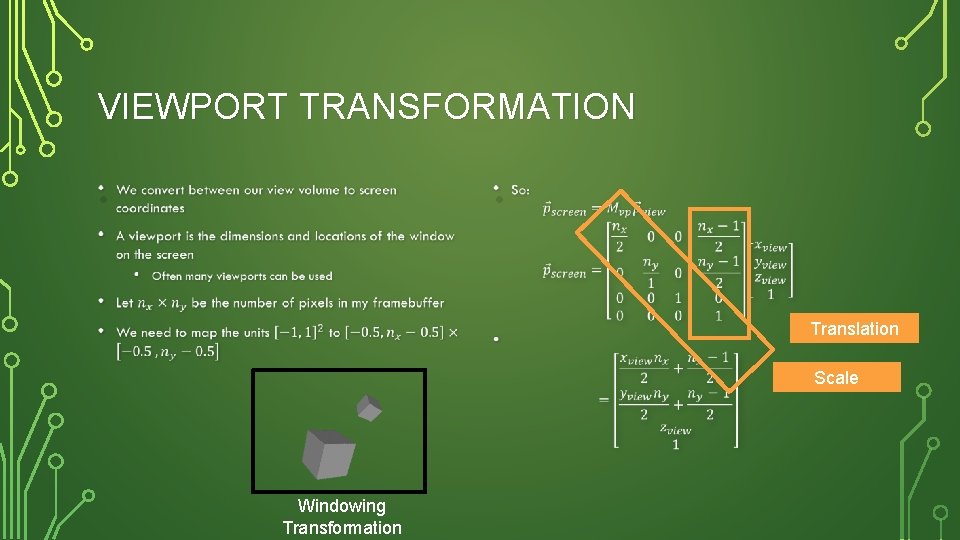
VIEWPORT TRANSFORMATION • • Translation Scale Windowing Transformation

VIEWPORT TRANSFORMATION • Easy method in gl for the viewport • gl. Viewport(x, y, width, height) • Note the slight difference in parameters from the viewing, i. e. , there is an offset here. Windowing Transformation

COMPOSING THE MATRICES •

ACTIVITY •

CONCLUSIONS • We can't get away from the math! • Properties give us faster algorithms and correct pictures • We have to reason about our appropriate coordinate frame • Always ensure sets of points/vectors are defined based on the same basis