Introduction to Theoretical Computer Science COMP 335 Fall














![Equivalence Classes For an equivalence relation R, we define equivalence class of x [x]R Equivalence Classes For an equivalence relation R, we define equivalence class of x [x]R](https://slidetodoc.com/presentation_image_h/83fd7ef7d1044f2811bf366e29e1a96d/image-21.jpg)











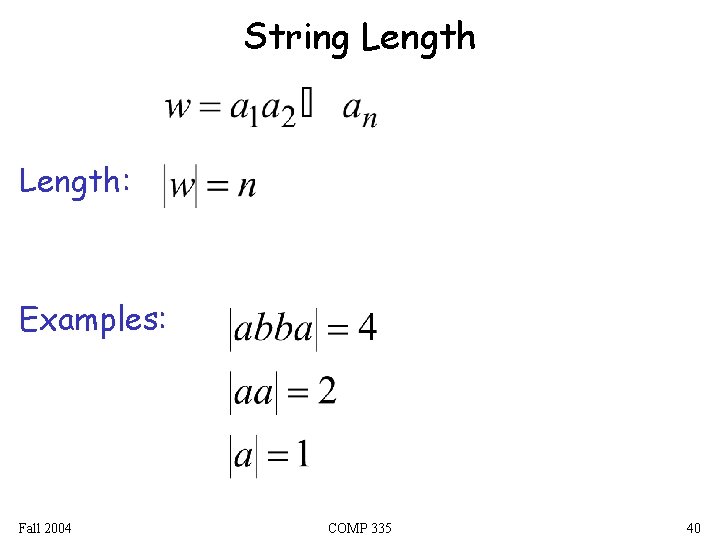














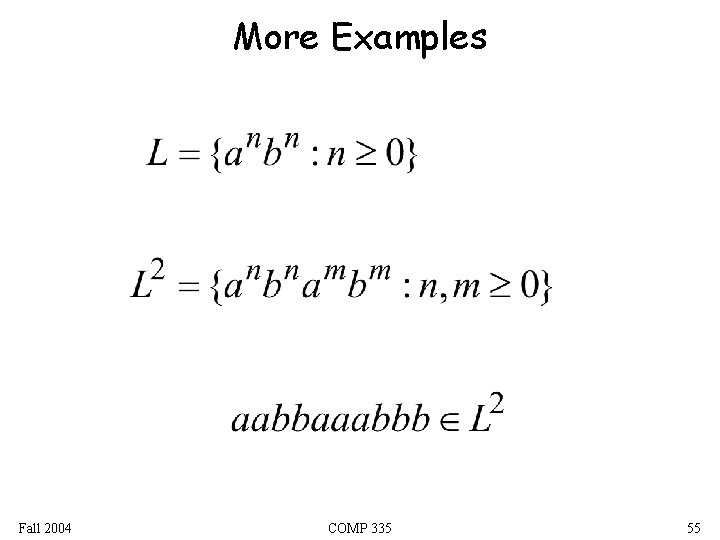


- Slides: 57

Introduction to Theoretical Computer Science COMP 335 Fall 2004 Slides by Costas Busch, Rensselaer Polytechnic Institute, Modified by N. Shiri & G. Grahne, Concordia University Fall 2004 COMP 335 1

• This course: A study of abstract models of computers and computation. • Why theory, when computer field is so practical? • Theory provides concepts and principles, for both hardware and software that help us understand the general nature of the field. Fall 2004 COMP 335 2

Mathematical Preliminaries Fall 2004 COMP 335 3

Mathematical Preliminaries • Sets • Functions • Relations • Graphs • Proof Techniques Fall 2004 COMP 335 4

SETS A set is a collection of elements We write Fall 2004 COMP 335 5

Set Representations C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } finite set S = { 2, 4, 6, … } infinite set S = { j : j > 0, and j = 2 k for k>0 } S = { j : j is nonnegative and even } Fall 2004 COMP 335 6

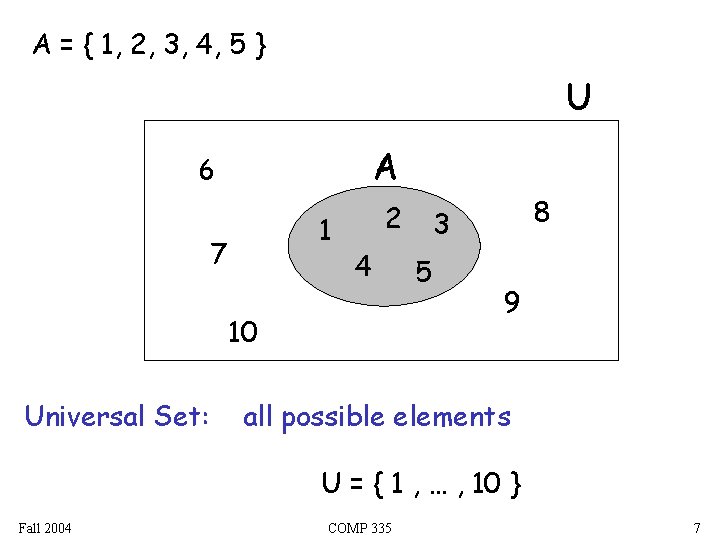
A = { 1, 2, 3, 4, 5 } U A 6 1 7 2 4 10 Universal Set: 8 3 5 9 all possible elements U = { 1 , … , 10 } Fall 2004 COMP 335 7

Set Operations A = { 1, 2, 3 } B = { 2, 3, 4, 5} B A • Union A U B = { 1, 2, 3, 4, 5 } 2 3 1 4 5 • Intersection U A B = { 2, 3 } 2 3 • Difference A-B={1} 1 B - A = { 4, 5 } Venn diagrams Fall 2004 COMP 335 8

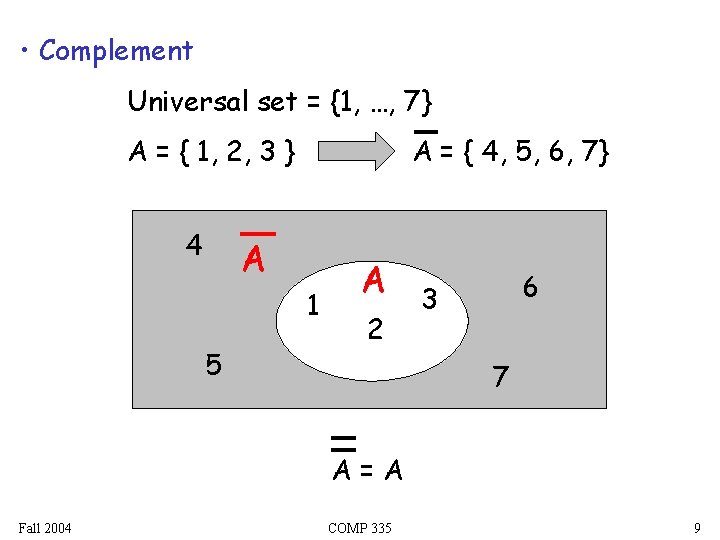
• Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A = { 4, 5, 6, 7} A 1 5 A 2 6 3 7 A=A Fall 2004 COMP 335 9

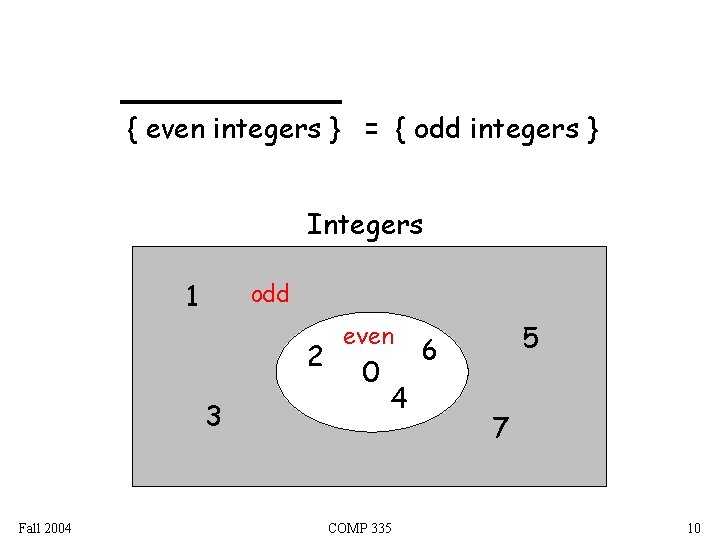
{ even integers } = { odd integers } Integers 1 odd 2 3 Fall 2004 even 0 4 COMP 335 5 6 7 10

De. Morgan’s Laws Fall 2004 U AUB=A B B=AUB COMP 335 11

Empty, Null Set: ={} SU =S S = U S- = Universal Set =S -S= Fall 2004 COMP 335 12

Subset A = { 1, 2, 3} B = { 1, 2, 3, 4, 5 } B U Proper Subset: A U A B B A Fall 2004 COMP 335 13

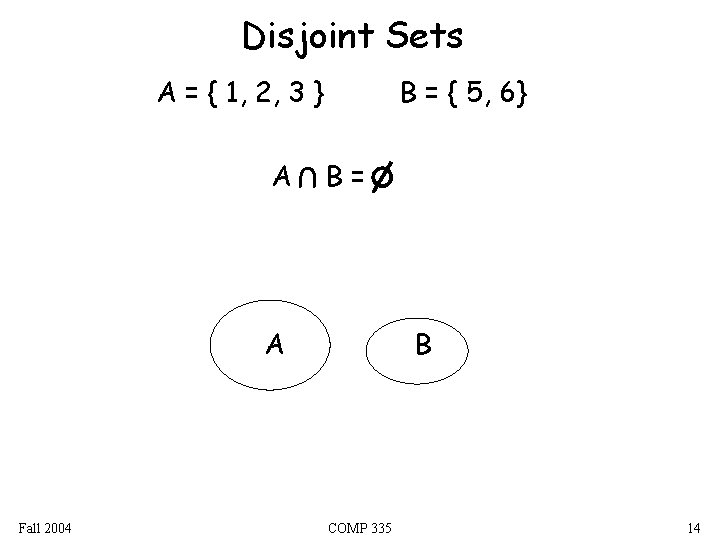
Disjoint Sets A = { 1, 2, 3 } U A B = { 5, 6} B= A Fall 2004 B COMP 335 14

Set Cardinality • For finite sets A = { 2, 5, 7 } |A| = 3 (set size) Fall 2004 COMP 335 15

Powersets A powerset is a set of sets S = { a, b, c } Powerset of S = the set of all the subsets of S 2 S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2 S | = 2|S| Fall 2004 COMP 335 ( 8 = 23 ) 16

Cartesian Product A = { 2, 4 } B = { 2, 3, 5 } A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 5) } |A X B| = |A|*|B| Generalizes to more than two sets AXBX…XZ Fall 2004 COMP 335 17

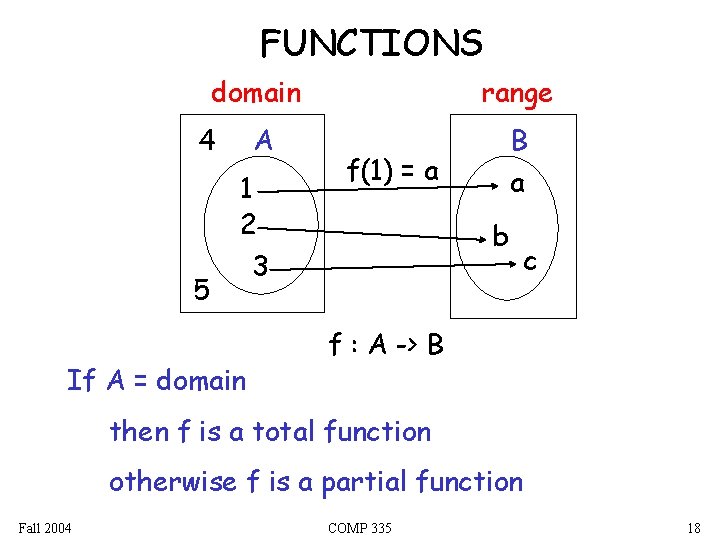
FUNCTIONS domain 4 5 A 1 2 3 If A = domain range B f(1) = a a b c f : A -> B then f is a total function otherwise f is a partial function Fall 2004 COMP 335 18

RELATIONS R = {(x 1, y 1), (x 2, y 2), (x 3, y 3), …} x i R yi e. g. if R = ‘>’: 2 > 1, 3 > 2, 3 > 1 Fall 2004 COMP 335 19

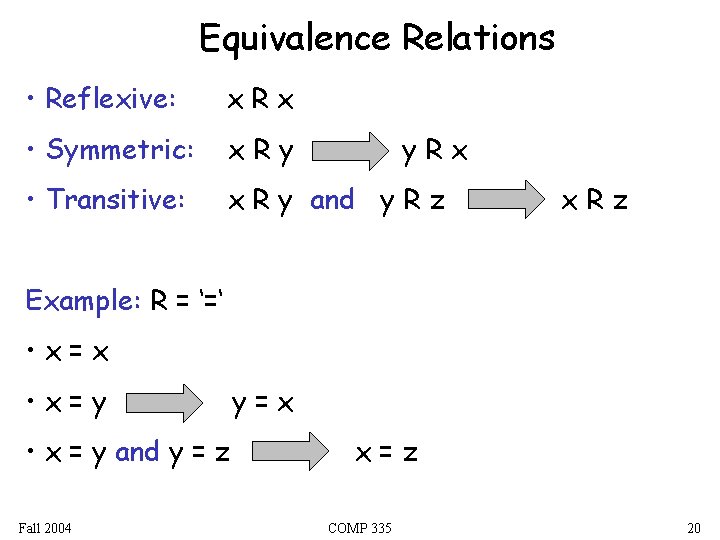
Equivalence Relations • Reflexive: x. Rx • Symmetric: x. Ry • Transitive: x R y and y R z y. Rx x. Rz Example: R = ‘=‘ • x=x • x=y • x = y and y = z Fall 2004 y=x x=z COMP 335 20
![Equivalence Classes For an equivalence relation R we define equivalence class of x xR Equivalence Classes For an equivalence relation R, we define equivalence class of x [x]R](https://slidetodoc.com/presentation_image_h/83fd7ef7d1044f2811bf366e29e1a96d/image-21.jpg)
Equivalence Classes For an equivalence relation R, we define equivalence class of x [x]R = {y : x R y} Example: R = { (1, 1), (2, 2), (1, 2), (2, 1), (3, 3), (4, 4), (3, 4), (4, 3) } Equivalence class of [1]R = {1, 2} Equivalence class of [3]R = {3, 4} Fall 2004 COMP 335 21

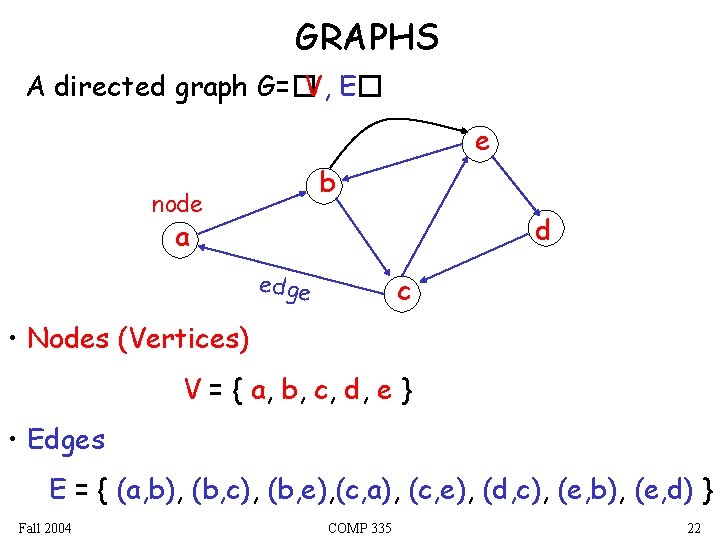
GRAPHS A directed graph G=�V, E� e b node d a edge c • Nodes (Vertices) V = { a, b, c, d, e } • Edges E = { (a, b), (b, c), (b, e), (c, a), (c, e), (d, c), (e, b), (e, d) } Fall 2004 COMP 335 22

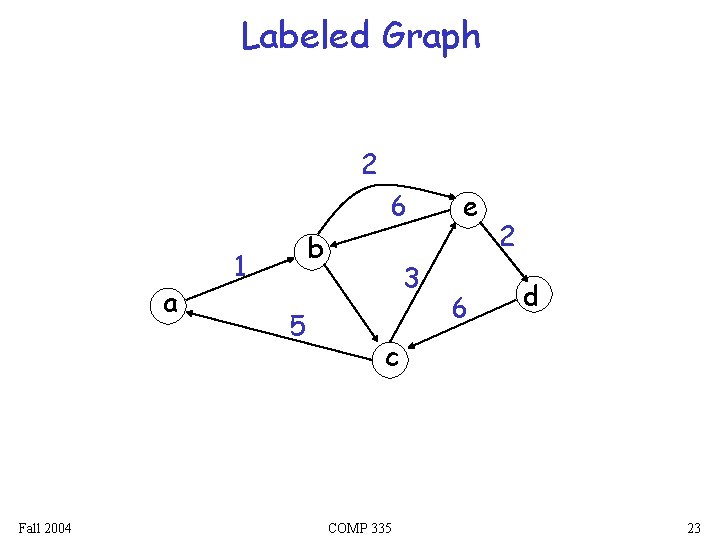
Labeled Graph 2 6 a Fall 2004 b 1 5 3 e 6 2 d c COMP 335 23

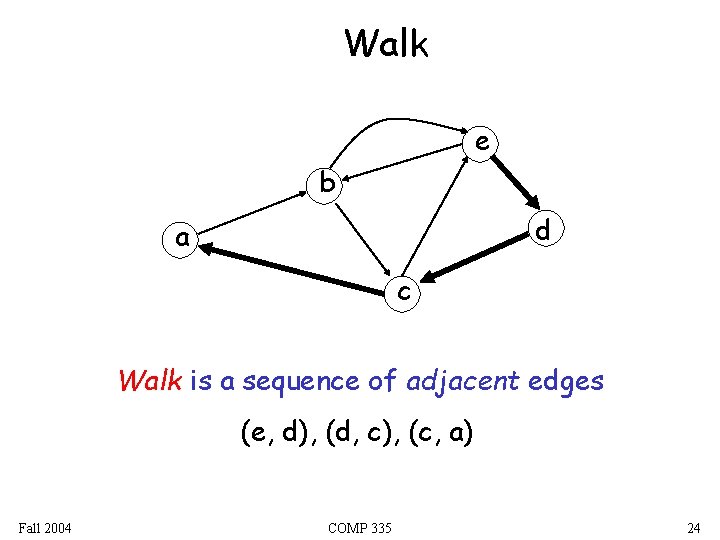
Walk e b d a c Walk is a sequence of adjacent edges (e, d), (d, c), (c, a) Fall 2004 COMP 335 24

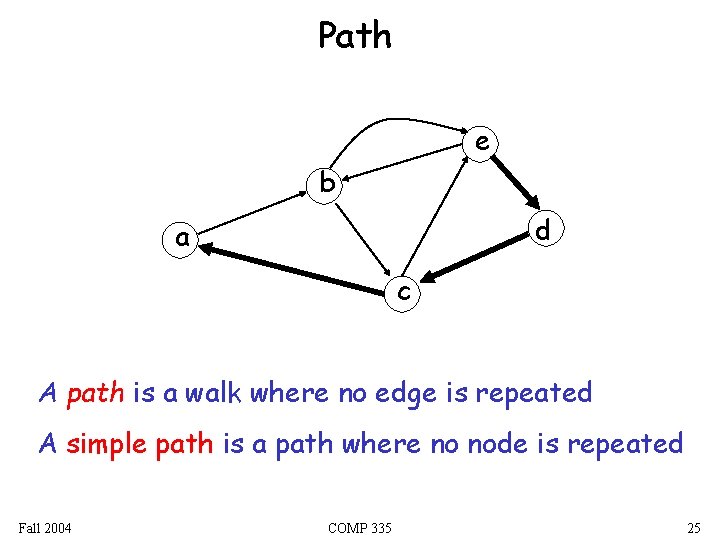
Path e b d a c A path is a walk where no edge is repeated A simple path is a path where no node is repeated Fall 2004 COMP 335 25

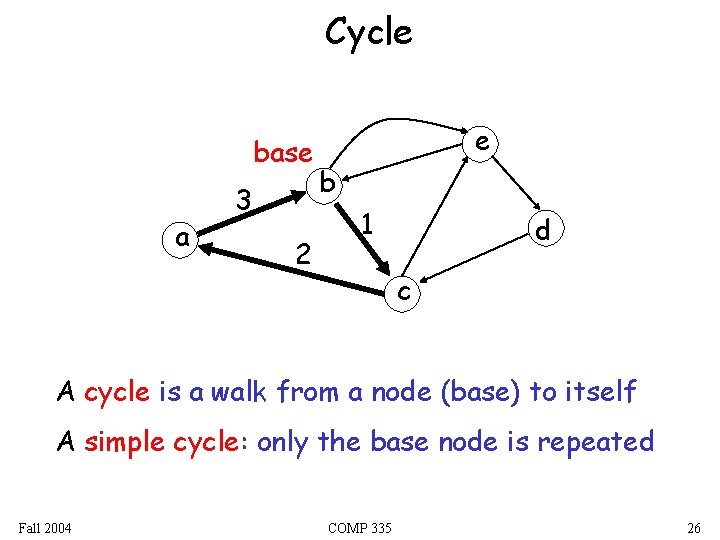
Cycle base a 3 2 e b 1 d c A cycle is a walk from a node (base) to itself A simple cycle: only the base node is repeated Fall 2004 COMP 335 26

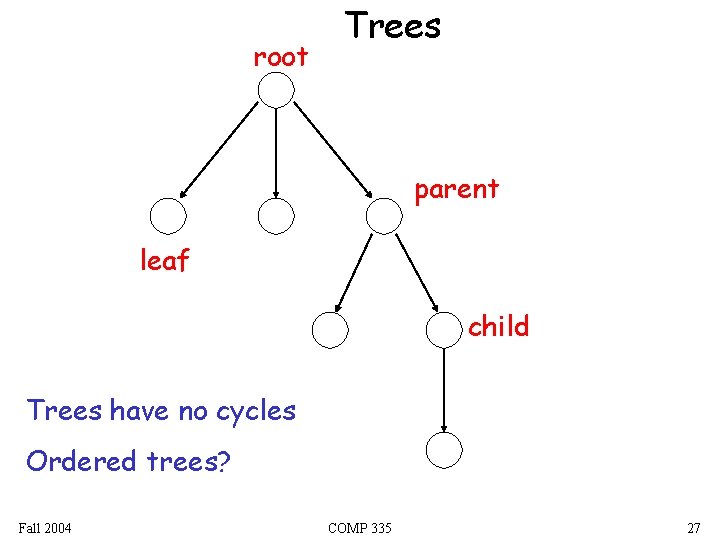
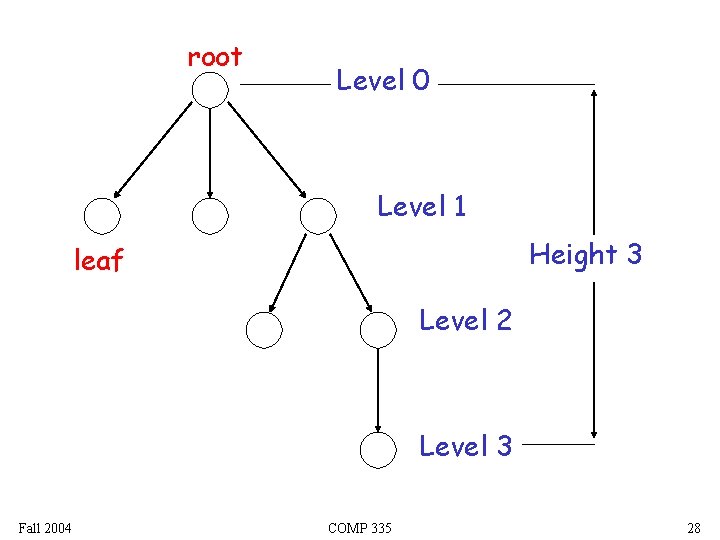
root Trees parent leaf child Trees have no cycles Ordered trees? Fall 2004 COMP 335 27

root Level 0 Level 1 Height 3 leaf Level 2 Level 3 Fall 2004 COMP 335 28

PROOF TECHNIQUES • Proof by induction • Proof by contradiction Fall 2004 COMP 335 29

Induction We have statements P 1, P 2, P 3, … If we know • for some b that P 1, P 2, …, Pb are true • for any k >= b that P 1, P 2, …, Pk imply Pk+1 Then Every Pi is true, that is, ∀i P(i) Fall 2004 COMP 335 30

Proof by Contradiction We want to prove that a statement P is true • we assume that P is false • then we arrive at an incorrect conclusion • therefore, statement P must be true Fall 2004 COMP 335 31

Example Theorem: is not rational Proof: Assume by contradiction that it is rational = n/m n and m have no common factors We will show that this is impossible Fall 2004 COMP 335 32

= n/m Therefore, 2 m 2 = 4 k 2 n 2 2 m 2 = n 2 is even m 2 = 2 k 2 n is even n=2 k m is even m=2 p Thus, m and n have common factor 2 Contradiction! Fall 2004 COMP 335 33

Pigeon Hole Principle: If n+1 objects are put into n boxes, then at least one box must contain 2 or more objects. Ex: Can show if 5 points are placed inside a square whose sides are 2 cm long at least one pair of points are at a distance ≤ 2 cm. According to the PHP, if we divide the square into 4, at least two of the points must be in one of these 4 squares. But the length of the diagonals of these squares is 2. the two points cannot be further apart than 2 cm. Fall 2004 COMP 335 34

Languages Fall 2004 COMP 335 35

A language is a set of strings String: A sequence of letters/symbols Examples: “cat”, “dog”, “house”, … Defined over an alphabet: Fall 2004 COMP 335 36

Alphabets and Strings We will use small alphabets: Strings Fall 2004 COMP 335 37

String Operations Concatenation Fall 2004 COMP 335 38

Reverse Fall 2004 COMP 335 39
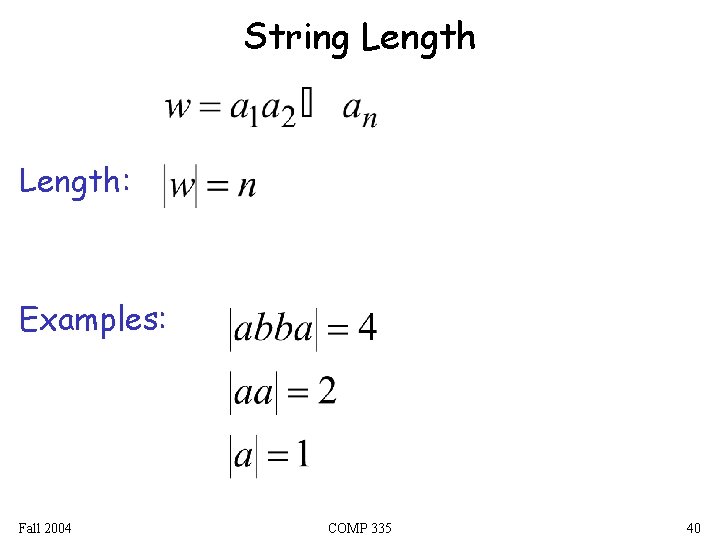
String Length: Examples: Fall 2004 COMP 335 40

Length of Concatenation Example: Fall 2004 COMP 335 41

The Empty String A string with no letters: Observations: Fall 2004 COMP 335 42

Substring of string: a subsequence of consecutive characters String Fall 2004 Substring COMP 335 43

Prefix and Suffix Prefixes Suffixes prefix suffix Fall 2004 COMP 335 44

Another Operation Example: Definition: Fall 2004 COMP 335 45

The * Operation : the set of all possible strings from alphabet Fall 2004 COMP 335 46

The + Operation : the set of all possible strings from alphabet except Fall 2004 COMP 335 47

Languages A language is any subset of Example: Languages: Fall 2004 COMP 335 48

Note that: Sets Set size String length Fall 2004 COMP 335 49

Another Example An infinite language Fall 2004 COMP 335 50

Operations on Languages The usual set operations Complement: Fall 2004 COMP 335 51

Reverse Definition: Examples: Fall 2004 COMP 335 52

Concatenation Definition: Example: Fall 2004 COMP 335 53

Another Operation Definition: Special case: Fall 2004 COMP 335 54
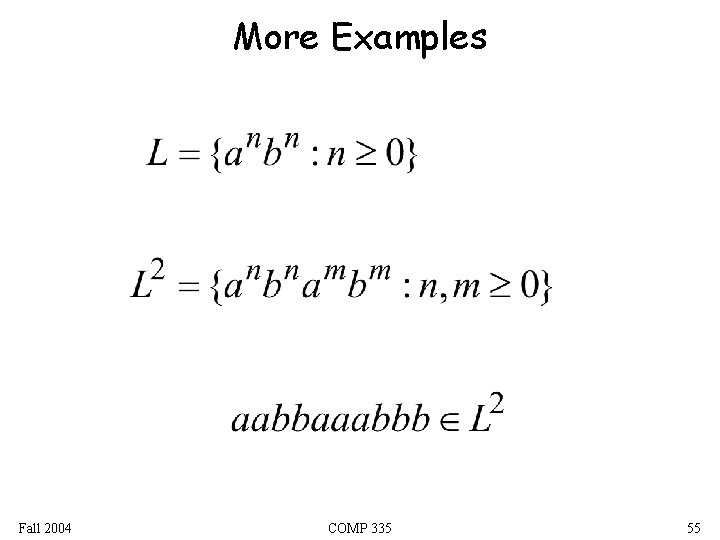
More Examples Fall 2004 COMP 335 55

Star-Closure (Kleene *) Definition: Example: Fall 2004 COMP 335 56

Positive Closure Definition: Fall 2004 COMP 335 57