Cinematica descrizione quantitativa del moto dei corpi Adesso

Cinematica (descrizione quantitativa del moto dei corpi) Adesso riprenderemo una serie di concetti e di grandezze fisiche di cui abbiamo già parlato e di cui abbiamo già fatto uso sia pure empiricamente e ne daremo la definizione formale e operativa. In particolare: Posizione Spostamento Velocità Accelerazione Lo faremo prima per il caso unidimensionale e poi per i moti in due o tre dimensioni L’oggetto di cui studieremo il moto sarà un «punto materiale» , cioè uno oggetto privo di estensioni e quindi privo di fenomeni vibrazionali o rotazionali © Nichi D'Amico 1

Moto in una dimensione Posizione Spostamento Velocità Accelerazione © Nichi D'Amico 2

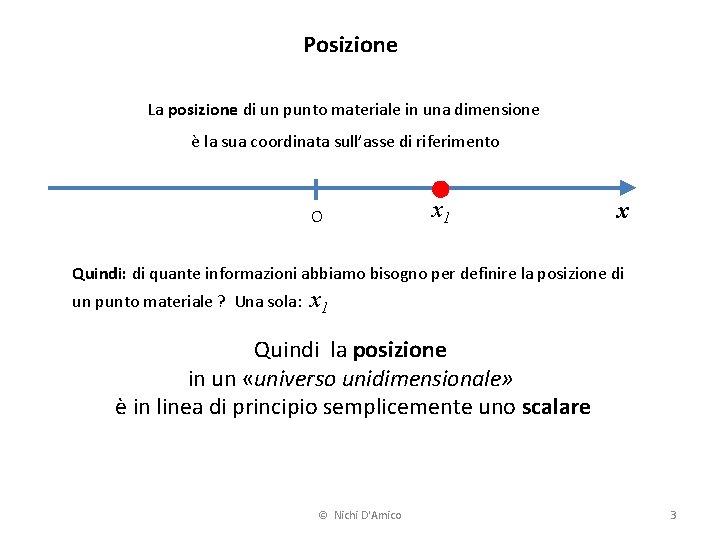
Posizione La posizione di un punto materiale in una dimensione è la sua coordinata sull’asse di riferimento O x 1 x Quindi: di quante informazioni abbiamo bisogno per definire la posizione di un punto materiale ? Una sola: x 1 Quindi la posizione in un «universo unidimensionale» è in linea di principio semplicemente uno scalare © Nichi D'Amico 3

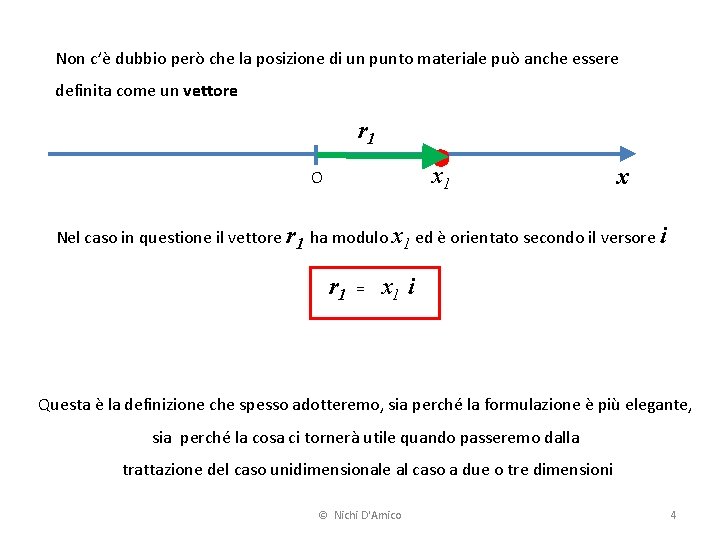
Non c’è dubbio però che la posizione di un punto materiale può anche essere definita come un vettore r 1 x 1 O x Nel caso in questione il vettore r 1 ha modulo x 1 ed è orientato secondo il versore i r 1 = x 1 i Questa è la definizione che spesso adotteremo, sia perché la formulazione è più elegante, sia perché la cosa ci tornerà utile quando passeremo dalla trattazione del caso unidimensionale al caso a due o tre dimensioni © Nichi D'Amico 4

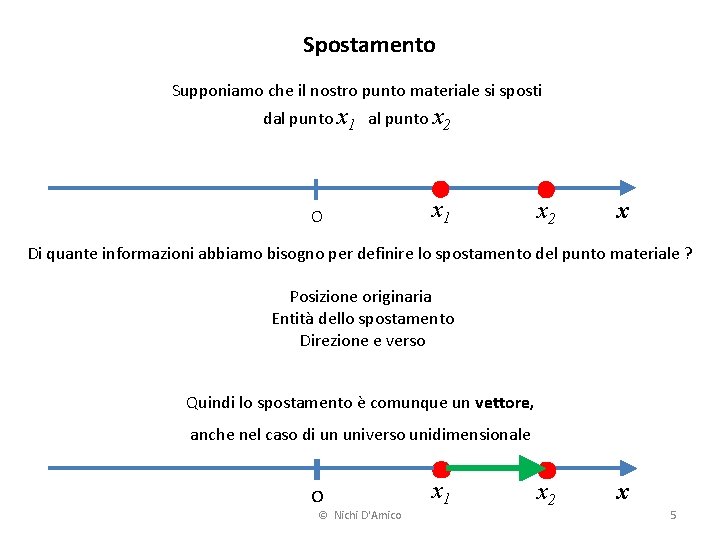
Spostamento Supponiamo che il nostro punto materiale si sposti dal punto x 1 al punto x 2 O x 1 x 2 x Di quante informazioni abbiamo bisogno per definire lo spostamento del punto materiale ? Posizione originaria Entità dello spostamento Direzione e verso Quindi lo spostamento è comunque un vettore, anche nel caso di un universo unidimensionale O © Nichi D'Amico x 1 x 2 x 5

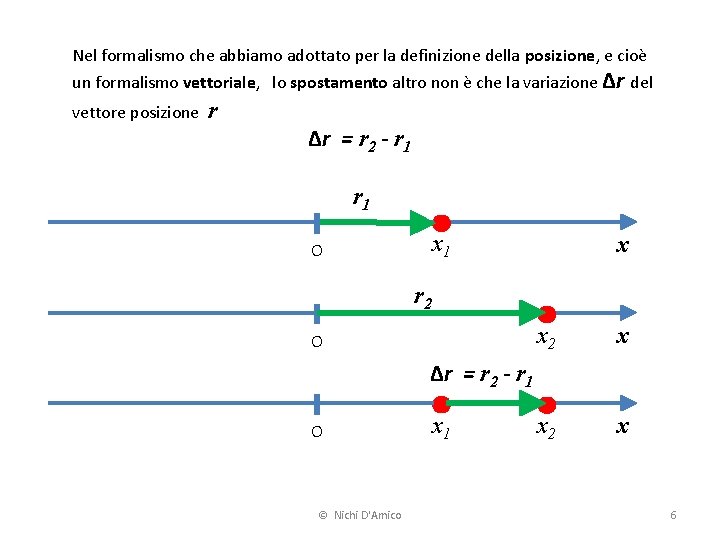
Nel formalismo che abbiamo adottato per la definizione della posizione, e cioè un formalismo vettoriale, lo spostamento altro non è che la variazione Δr del vettore posizione r Δr = r 2 - r 1 x 1 O x r 2 O x 2 x Δr = r 2 - r 1 O © Nichi D'Amico x 1 6

Velocità La velocità di un punto materiale è la rapidità con cui la sua posizione cambia nel tempo Quindi: se il nostro punto materiale effettua il suo spostamento da x 1 a Intervallo di tempo Δt: x 2 in un Δr = r 2 - r 1 O x 1 x 2 x Tempo impiegato Δt definiremo la velocità media come: v = Δr / Δt m/s La velocità così definita è detta velocità media in quanto la misura dello spostamento Δr e del tempo trascorso Δt non ci danno informazioni sull’effettivo moto effettuato dal punto materiale fra i punti x 1 e x 2 ed è un vettore, in quanto risulta dal rapporto fra un vettore (lo spostamento) ed uno scalare (il tempo). © Nichi D'Amico 7

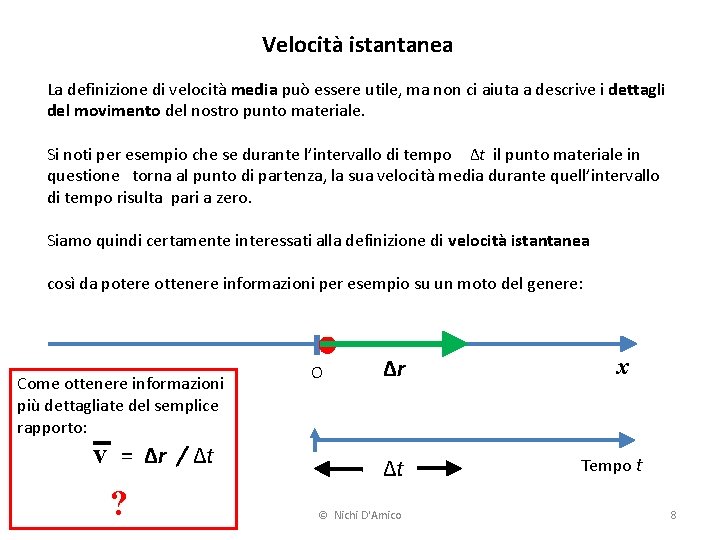
Velocità istantanea La definizione di velocità media può essere utile, ma non ci aiuta a descrive i dettagli del movimento del nostro punto materiale. Si noti per esempio che se durante l’intervallo di tempo Δt il punto materiale in questione torna al punto di partenza, la sua velocità media durante quell’intervallo di tempo risulta pari a zero. Siamo quindi certamente interessati alla definizione di velocità istantanea così da potere ottenere informazioni per esempio su un moto del genere: Come ottenere informazioni più dettagliate del semplice rapporto: v = Δr / Δt ? O Δr Δt © Nichi D'Amico x Tempo t 8

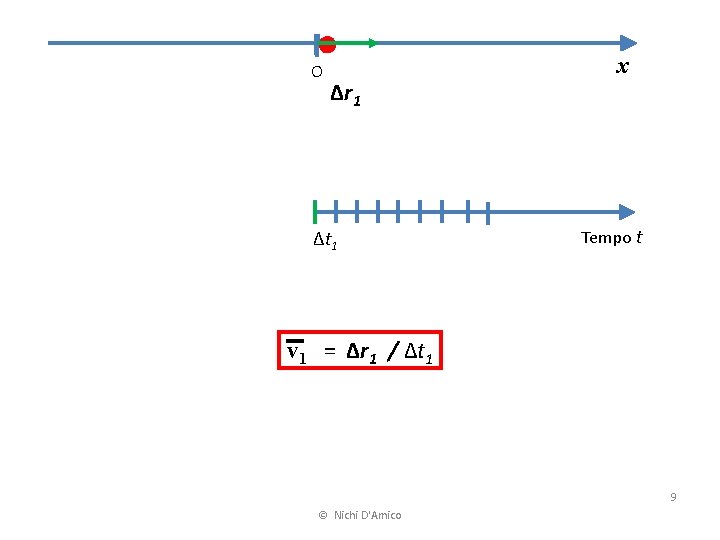
O Δr 1 Δt 1 x Tempo t v 1 = Δr 1 / Δt 1 9 © Nichi D'Amico

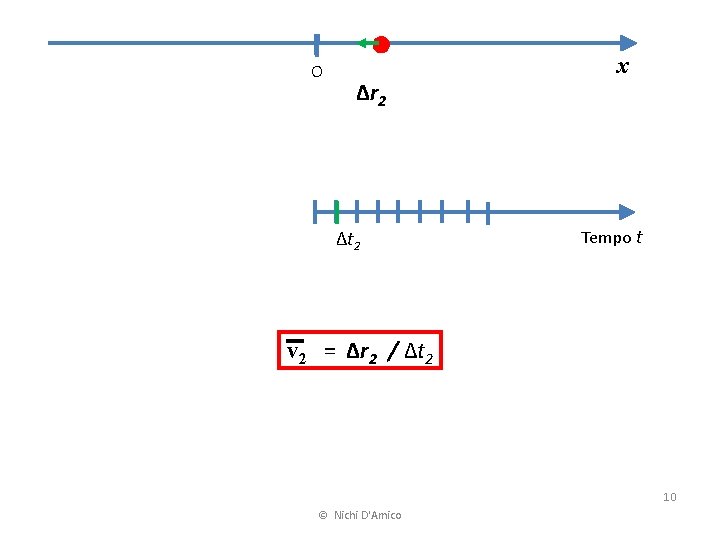
O Δr 2 Δt 2 x Tempo t v 2 = Δr 2 / Δt 2 10 © Nichi D'Amico

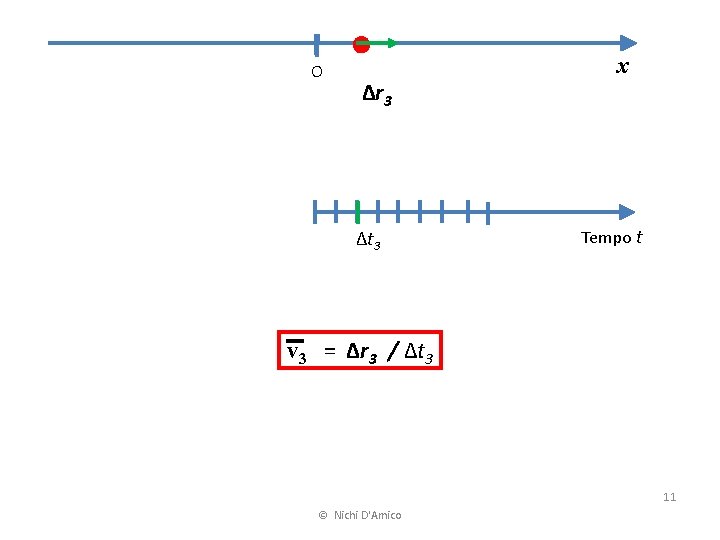
O Δr 3 Δt 3 x Tempo t v 3 = Δr 3 / Δt 3 11 © Nichi D'Amico

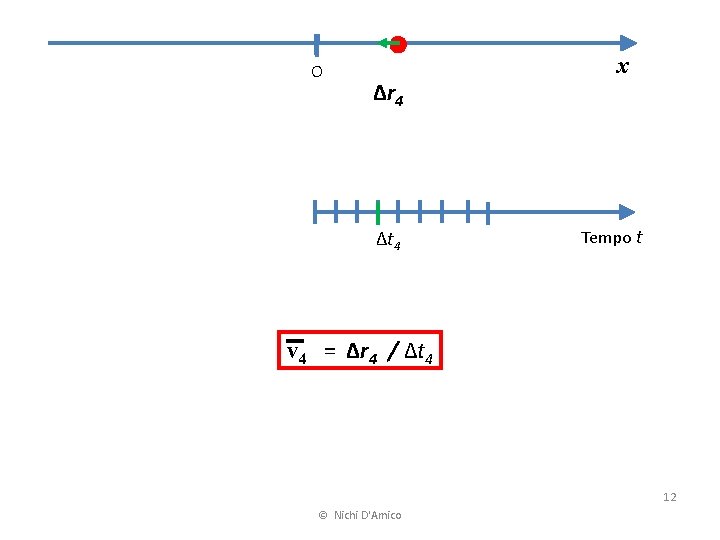
O Δr 4 Δt 4 x Tempo t v 4 = Δr 4 / Δt 4 12 © Nichi D'Amico

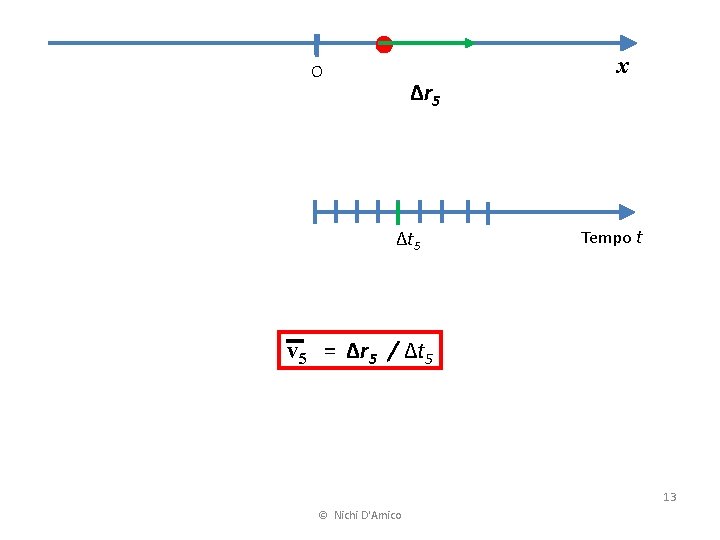
O Δr 5 Δt 5 x Tempo t v 5 = Δr 5 / Δt 5 13 © Nichi D'Amico

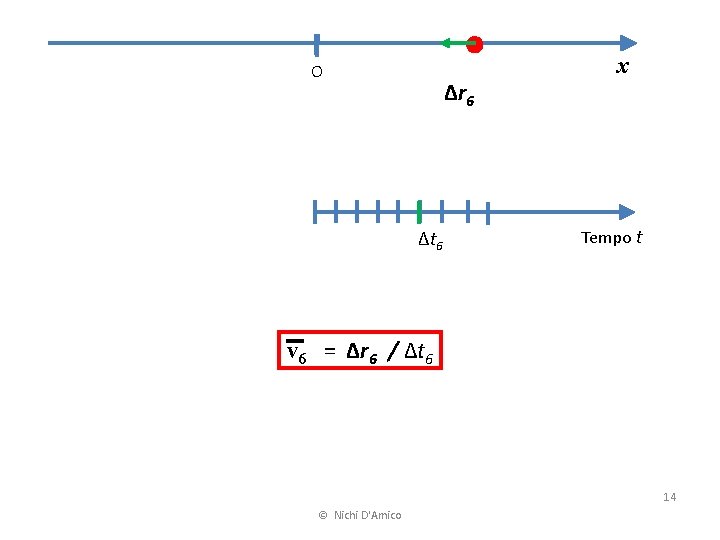
O Δr 6 Δt 6 x Tempo t v 6 = Δr 6 / Δt 6 14 © Nichi D'Amico

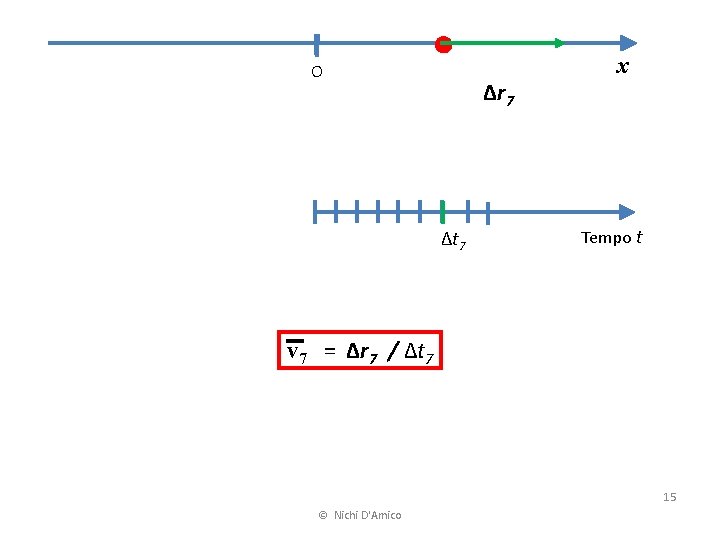
O Δr 7 Δt 7 x Tempo t v 7 = Δr 7 / Δt 7 15 © Nichi D'Amico

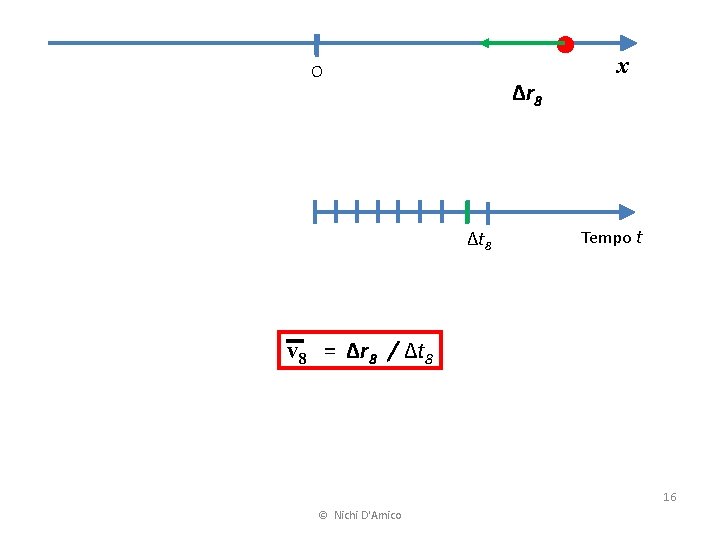
O Δr 8 Δt 8 x Tempo t v 8 = Δr 8 / Δt 8 16 © Nichi D'Amico

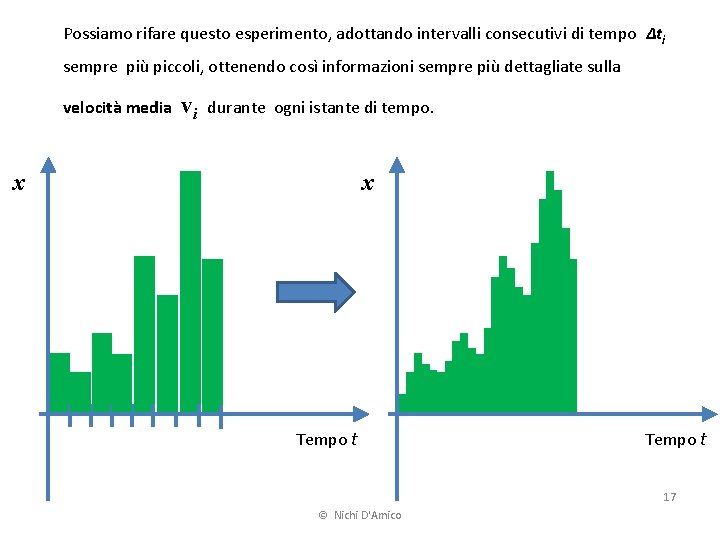
Possiamo rifare questo esperimento, adottando intervalli consecutivi di tempo Δti sempre più piccoli, ottenendo così informazioni sempre più dettagliate sulla velocità media vi durante ogni istante di tempo. x x Tempo t 17 © Nichi D'Amico

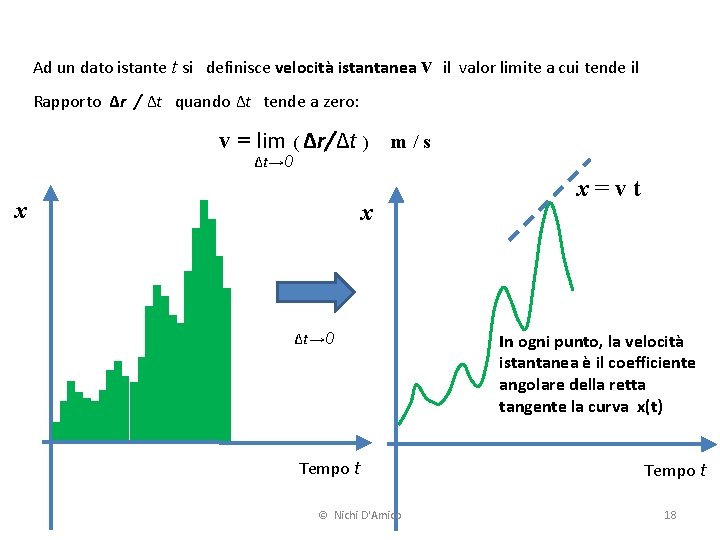
Ad un dato istante t si definisce velocità istantanea v il valor limite a cui tende il Rapporto Δr / Δt quando Δt tende a zero: v = lim ( Δr/Δt ) m / s Δt→ 0 x x Δt→ 0 Tempo t © Nichi D'Amico x=vt In ogni punto, la velocità istantanea è il coefficiente angolare della retta tangente la curva x(t) Tempo t 18

Il limite: v = lim ( Δr/Δt ) è la definizione matematica di derivata: v = dr/dt che nel caso unidimensionale in questione si riduce a: vx = dx/dt mentre in generale la derivata di un vettore in uno spazio tridimensionale (x, y, z) sarà data dalla somma delle derivate delle sue componenti: v = dr dt = d dy dx dz i + j + k (xi + yj + zk) = dt dt v = vx i + vy j + vz k © Nichi D'Amico 19

Accelerazione Come abbiamo visto, in generale la velocità istantanea di un punto materiale in movimento può cambiare nel tempo, e questo porta alla definizione di un’altra grandezza fisica: l’accelerazione. Così come la velocità esprime la rapidità con cui il punto materiale cambia la sua posizione, l’accelerazione esprime la rapidità con cui il punto materiale cambia la sua velocità. Se un punto materiale ad un dato istante t 1 si muove con velocità v 1 e ad un altro dato istante t 2 si muove con velocità v 2 l’accelerazione media a è data dal rapporto: a = (v 2 – v 1) / (t 2 – t 1) = Δv / Δt © Nichi D'Amico m / s 2 20

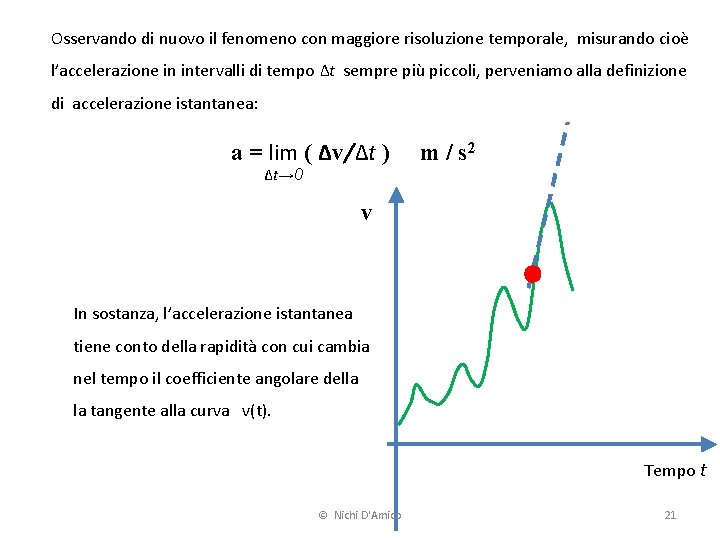
Osservando di nuovo il fenomeno con maggiore risoluzione temporale, misurando cioè l’accelerazione in intervalli di tempo Δt sempre più piccoli, perveniamo alla definizione di accelerazione istantanea: a = lim ( Δv/Δt ) Δt→ 0 m / s 2 v In sostanza, l’accelerazione istantanea tiene conto della rapidità con cui cambia nel tempo il coefficiente angolare della la tangente alla curva v(t). Tempo t © Nichi D'Amico 21

Anche in questo caso il limite: a = lim ( Δv/Δt ) è la definizione matematica di derivata: a = dv/dt che nel caso unidimensionale in questione si riduce a: ax = dvx/dt Anche in questo caso, in generale la derivata di un vettore in uno spazio tridimensionale (x, y, z) sarà data dalla somma delle derivate delle sue componenti: a = dv dt = d dvy dvx dv i+ j + zk (vxi + vyj + vzk) = dt dt a = ax i + ay j + az k © Nichi D'Amico 22

Dalle relazioni: ax = dvx /dt ay = dvy /dt az = dvz /dt vy = dy /dt vz = dz /dt e dalle: vx = dx /dt Risulta: ax = dvx /dt = d 2 x /dt 2 ay = dvy /dt = d 2 y /dt 2 az = dvz /dt = d 2 z /dt 2 Risulta quindi che l’accelerazione è©la. Nichi derivata seconda della posizione D'Amico 23

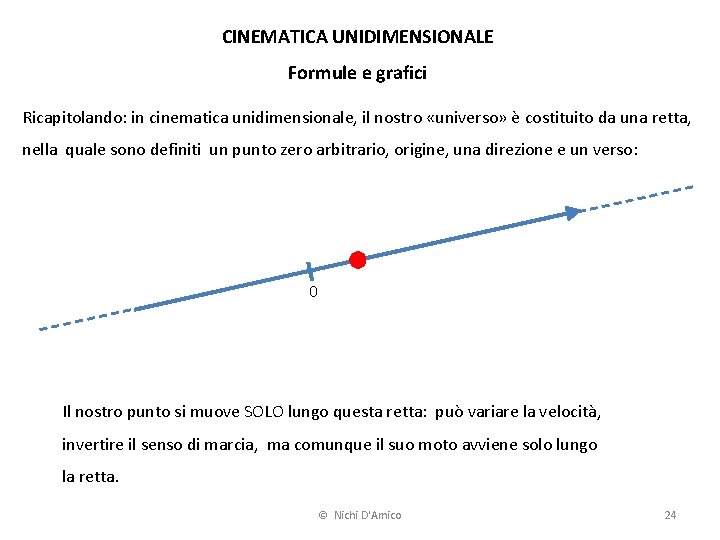
CINEMATICA UNIDIMENSIONALE Formule e grafici Ricapitolando: in cinematica unidimensionale, il nostro «universo» è costituito da una retta, nella quale sono definiti un punto zero arbitrario, origine, una direzione e un verso: 0 Il nostro punto si muove SOLO lungo questa retta: può variare la velocità, invertire il senso di marcia, ma comunque il suo moto avviene solo lungo la retta. © Nichi D'Amico 24

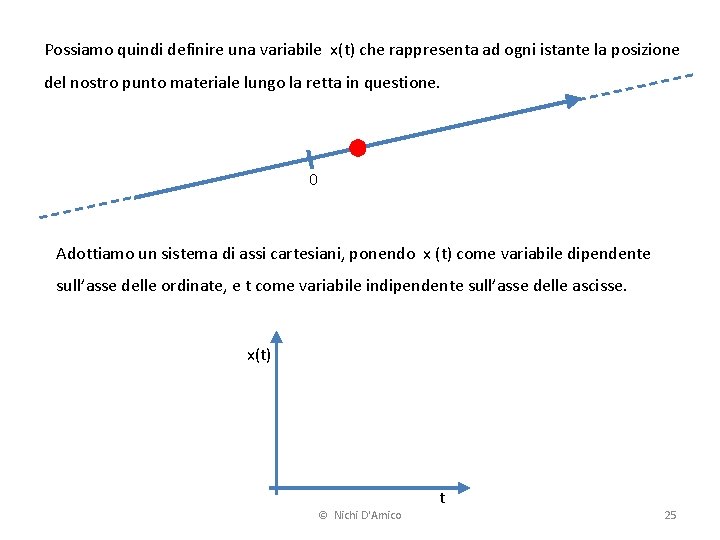
Possiamo quindi definire una variabile x(t) che rappresenta ad ogni istante la posizione del nostro punto materiale lungo la retta in questione. 0 Adottiamo un sistema di assi cartesiani, ponendo x (t) come variabile dipendente sull’asse delle ordinate, e t come variabile indipendente sull’asse delle ascisse. x(t) © Nichi D'Amico t 25

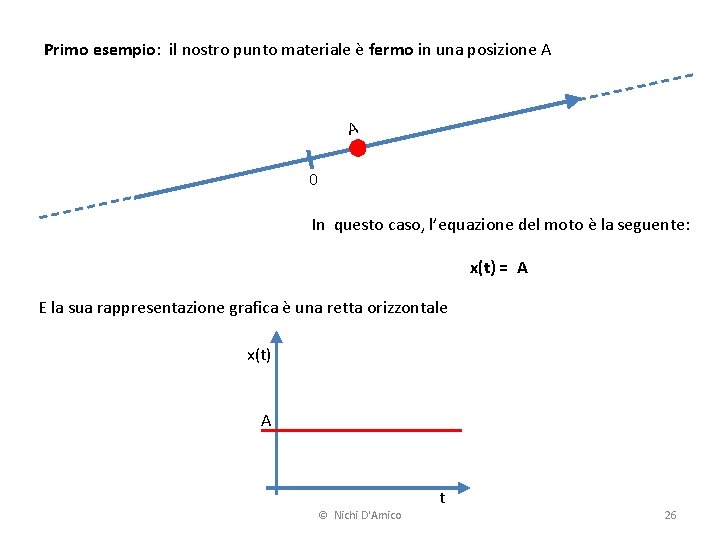
Primo esempio: il nostro punto materiale è fermo in una posizione A A 0 In questo caso, l’equazione del moto è la seguente: x(t) = A E la sua rappresentazione grafica è una retta orizzontale x(t) A © Nichi D'Amico t 26

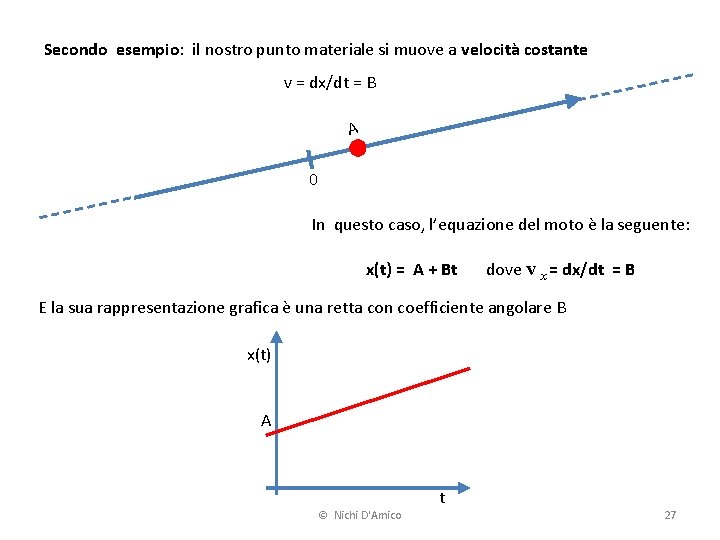
Secondo esempio: il nostro punto materiale si muove a velocità costante v = dx/dt = B A 0 In questo caso, l’equazione del moto è la seguente: x(t) = A + Bt dove v x = dx/dt = B E la sua rappresentazione grafica è una retta con coefficiente angolare B x(t) A © Nichi D'Amico t 27

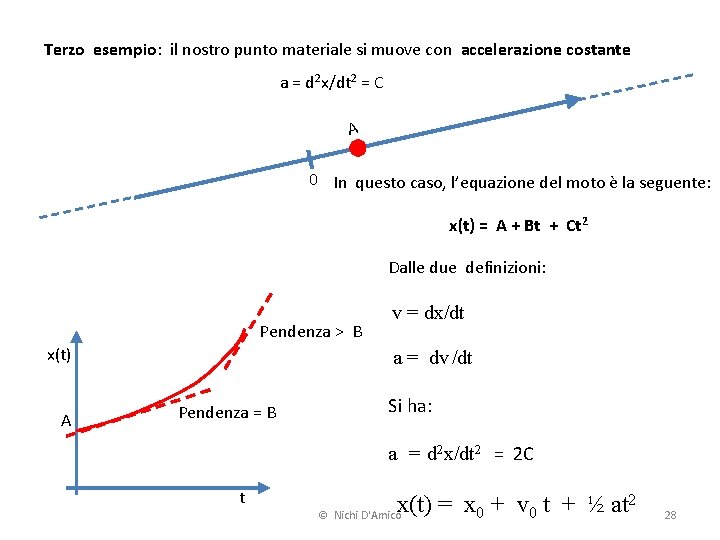
Terzo esempio: il nostro punto materiale si muove con accelerazione costante a = d 2 x/dt 2 = C A 0 In questo caso, l’equazione del moto è la seguente: x(t) = A + Bt + Ct 2 Dalle due definizioni: Pendenza > B x(t) A v = dx/dt a = dv /dt Pendenza = B Si ha: a = d 2 x/dt 2 = 2 C t x(t) = x 0 + v 0 t + ½ at 2 © Nichi D'Amico 28

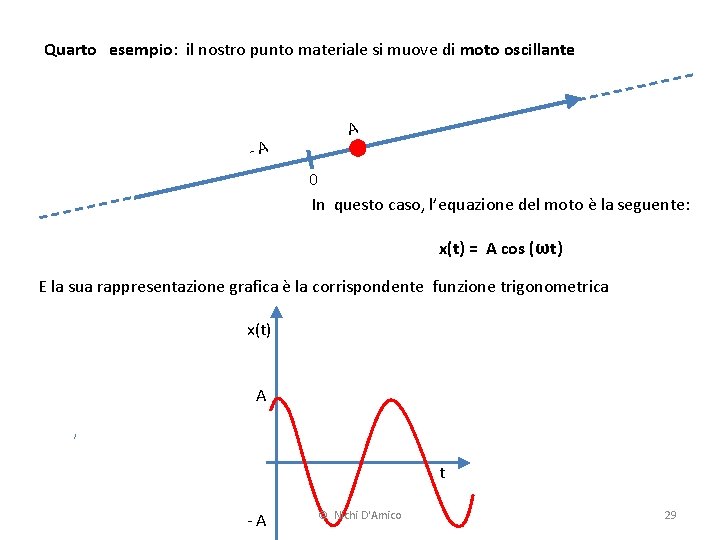
Quarto esempio: il nostro punto materiale si muove di moto oscillante -A A 0 In questo caso, l’equazione del moto è la seguente: x(t) = A cos (ωt) E la sua rappresentazione grafica è la corrispondente funzione trigonometrica x(t) A t -A © Nichi D'Amico 29

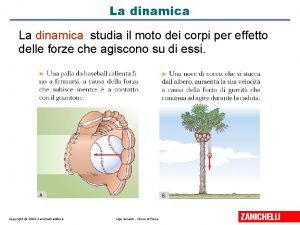
Moto di un corpo in caduta libera Un dato sperimentale: tutti i corpi, indipendentemente dalla loro forma, dimensione, sostanza, etc… cadono per terra con la medesima accelerazione. Apparentemente questo potrebbe sembrarci semplicemente falso, perché nel nostro immaginario, una foglia e una biglia acquisiscono accelerazioni differenti nella caduta a terra. In effetti normalmente nella nostra esperienza quotidiana, i corpi NON sono in caduta libera L’aria è un fluido: la foglia in pratica galleggia in questo fluido, mentre la biglia, soprattutto se di piccole dimensioni, risente poco dell’attrito con l’aria. Ma nel vuoto tutti i corpi in caduta libera acquisiscono la stessa accelerazione g © Nichi D'Amico 30

In prossimità della superficie terrestre, g = 9. 8 m / s 2 Definiamo allora il nostro sistema di riferimento e applichiamo le equazioni del moto Assumiamo come asse la direzione verticale y e fissiamone il verso positivo verso l’alto. a = costante = y -g In analogia con quanto abbiamo già discusso, le equazioni del moto saranno pertanto: y = y 0 + v 0 t – ½ gt 2 0 © Nichi D'Amico 31