Chapter 9 Inferences for Two Samples Yunming Mu

Chapter 9: Inferences for Two –Samples Yunming Mu Department of Statistics Texas A&M University

Outline 1 Overview 2 Inferences about Two Means: Independent and Small Samples 3 Inferences about Two Means: Independent and Large Samples 4 Inferences about Two Proportions 5 Inferences about Two Means: Matched Pairs

Overview There are many important and meaningful situations in which it becomes necessary to compare two sets of sample data.

Definitions Two Samples: Independent The sample values selected from one population are not related or somehow paired with the sample values selected from the other population. If the values in one sample are related to the values in the other sample, the samples are dependent. Such samples are often referred to as matched pairs or paired samples.

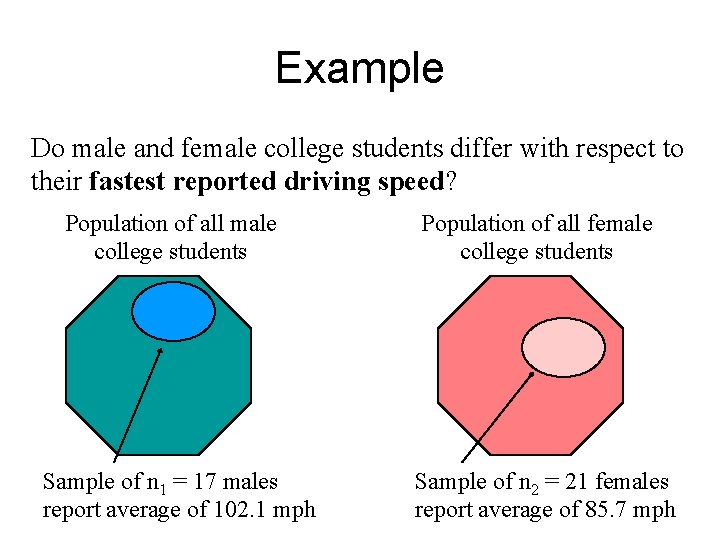
Example Do male and female college students differ with respect to their fastest reported driving speed? Population of all male college students Sample of n 1 = 17 males report average of 102. 1 mph Population of all female college students Sample of n 2 = 21 females report average of 85. 7 mph

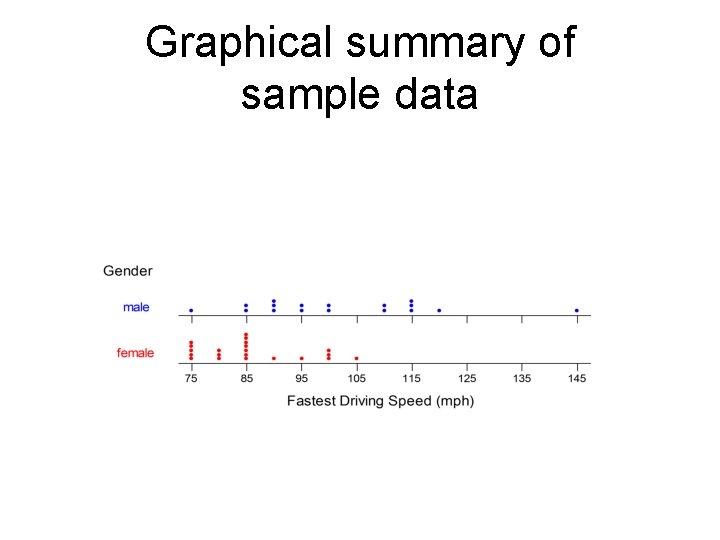
Graphical summary of sample data

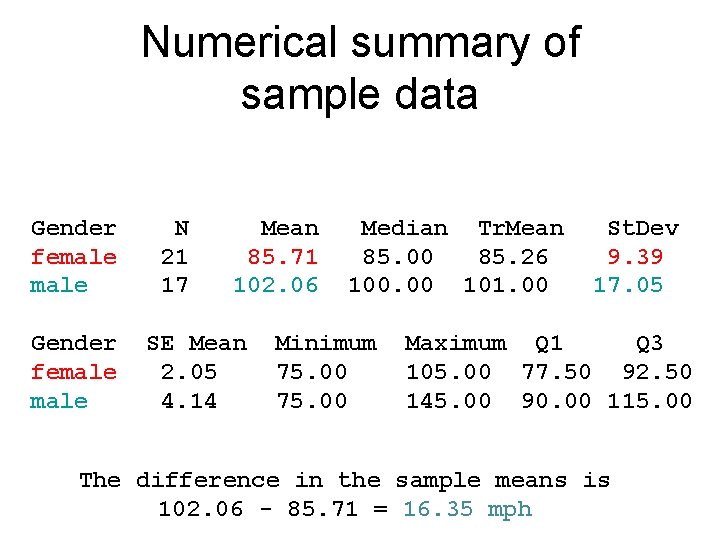
Numerical summary of sample data Gender female N 21 17 Mean 85. 71 102. 06 SE Mean 2. 05 4. 14 Median Tr. Mean 85. 00 85. 26 100. 00 101. 00 Minimum 75. 00 St. Dev 9. 39 17. 05 Maximum Q 1 Q 3 105. 00 77. 50 92. 50 145. 00 90. 00 115. 00 The difference in the sample means is 102. 06 - 85. 71 = 16. 35 mph

The Question in Statistical Notation Let M = the average fastest speed of all male students. and F = the average fastest speed of all female students. Then we want to know whether M F. This is equivalent to knowing whether M - F 0

All possible questions in statistical notation In general, we can always compare two averages by seeing how their difference compares to 0:

Set up hypotheses • Null hypothesis: – H 0: M = F [equivalent to M - F = 0] • Alternative hypothesis: – Ha: M F [equivalent to M - F 0]

Inferences about Two Means: Independent and Small Samples

Pooled Two-Sample T Test and T Interval Assumptions: 1. The two samples are independent. 2. Both samples are normal or the two sample sizes are small, n 1 < 30 and n 2 < 30 3. Both variances are unknown but equal. Assume variances are equal only if neither sample standard deviation is more than twice that of the other sample standard deviation.

Confidence Intervals Normal Samples w/ Unknown Equal Variance (x 1 - x 2) - E < (µ 1 - µ 2) < (x 1 - x 2) + E where

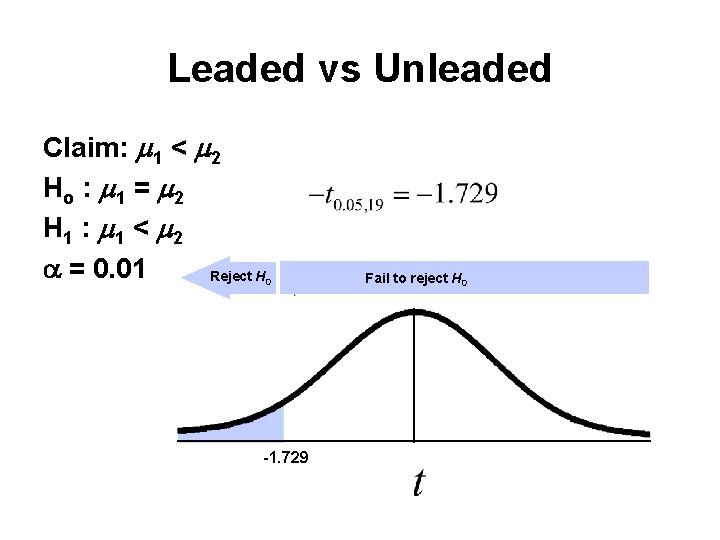
Leaded vs Unleaded Each of the cars selected for the EPA study was tested and the number of miles per gallon for each was obtained and recorded (Leaded=1 and Unleaded=2). Leaded (1) Unleaded(2) n 11 x 17. 2 S 2. 1 10 19. 9 2

95% Confidence Interval

Pooled Two-Sample T Tests Normal Samples w/ unknown Variance P-value: Use t distribution with n 1+n 2 -2 degrees of freedom and find the P-value by following the same procedure for t tests summarized in Ch 8. Critical values: Based on the significance level , use for upper tail tests, use for lower tail tests and use for two tailed tests.

Leaded vs Unleaded Claim: 1 < 2 Ho : 1 = 2 H 1 : 1 < 2 = 0. 01 Reject H 0 -1. 729 Fail to reject H 0

Leaded vs Unleaded Pooled Two-Sample T Test Claim: 1 < 2 Ho : 1 = 2 H 1 : 1 < 2 = 0. 05

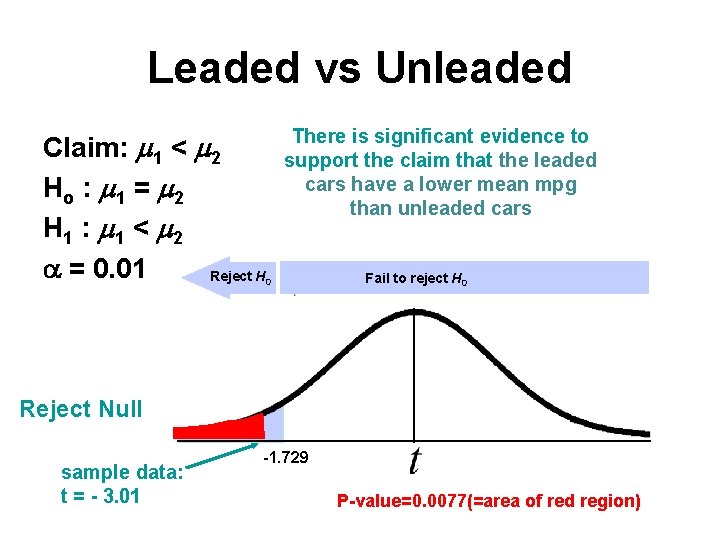
Leaded vs Unleaded Claim: 1 < 2 Ho : 1 = 2 H 1 : 1 < 2 = 0. 01 Reject H There is significant evidence to support the claim that the leaded cars have a lower mean mpg than unleaded cars 0 Fail to reject H 0 Reject Null sample data: t = - 3. 01 -1. 729 P-value=0. 0077(=area of red region)

Two-Sample T Test and T Interval Assumptions: 1. The two samples are independent. 2. Both samples are normal or the two sample sizes are small, n 1 < 30 and n 2 < 30 3. Both variances are unknown but unequal

Confidence Intervals Normal Samples w/ Unknown Unequal Variance (x 1 - x 2) - E < (µ 1 - µ 2) < (x 1 - x 2) + E where (round v down to the nearest integer)

Unpooled Two Sample T-Test Normal Samples w/ Unknown Variance P-value: Use t distribution with v degrees of freedom and find the P-value by following the same procedure for t tests summarized in Ch 8. Critical values: Based on the significance level , use for upper tail tests, use for lower tail tests and use for two tailed tests.

Example We compare the density of two different types of brick. Assuming normality of the two densities distributions and unequal unknown variances, test if there is a difference in the mean densities of two different types of brick. Type I brick Type 2 brick n 6 5 x 22. 73 21. 95 S 0. 10 0. 24

Unpooled Two-Sample T-Test Ho : 1 = 2 H 1 : 1 2 = 0. 05 P-Value = 0. 001; Reject the null and conclude that there is significant difference in the mean densities of the two types of brick

Two-sample t-test in Minitab • Select Stat. Select Basic Statistics. • Select 2 -sample t to get a Pop-Up window. • Click on the radio button before Samples in one Column. Put the measurement variable in Samples box, and put the grouping variable in Subscripts box. • Specify your alternative hypothesis. • If appropriate, select Assume Equal Variances. • Select OK.

Pooled two-sample t-test Two sample T for Fastest Gender female N 21 17 Mean 85. 71 102. 1 St. Dev 9. 39 17. 1 SE Mean 2. 0 4. 1 95% CI for mu (female) - mu (male ): ( -25. 2, -7. 5) T-Test mu (female) = mu (male ) (vs not =): T = -3. 75 P = 0. 0006 DF = 36 Both use Pooled St. Dev = 13. 4

(Unpooled) two-sample t-test Two sample T for Fastest Gender female N 21 17 Mean 85. 71 102. 1 St. Dev 9. 39 17. 1 SE Mean 2. 0 4. 1 95% CI for mu (female) - mu (male ): ( -25. 9, -6. 8) T-Test mu (female) = mu (male ) (vs not =): T = -3. 54 P = 0. 0017 DF = 23