Chapter 7 Trees Make Money Fast Stock Fraud




















- Slides: 34

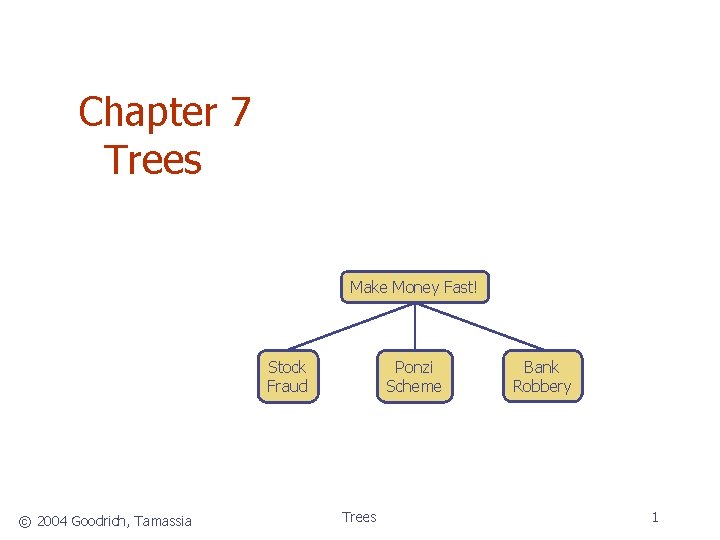
Chapter 7 Trees Make Money Fast! Stock Fraud © 2004 Goodrich, Tamassia Ponzi Scheme Trees Bank Robbery 1

7. 1 General Trees Tree is one of the most important non-linear Data Structures in computing. Tree structures are important because they allow us to implement a host of algorithms much faster than when using linear data structures, such as list. Trees also provide a natural way to organize data in many areas such as: n n n File systems Graphical User Interfaces (GUI) Databases Web Sites and many other computer systems. © 2004 Goodrich, Tamassia Trees 2

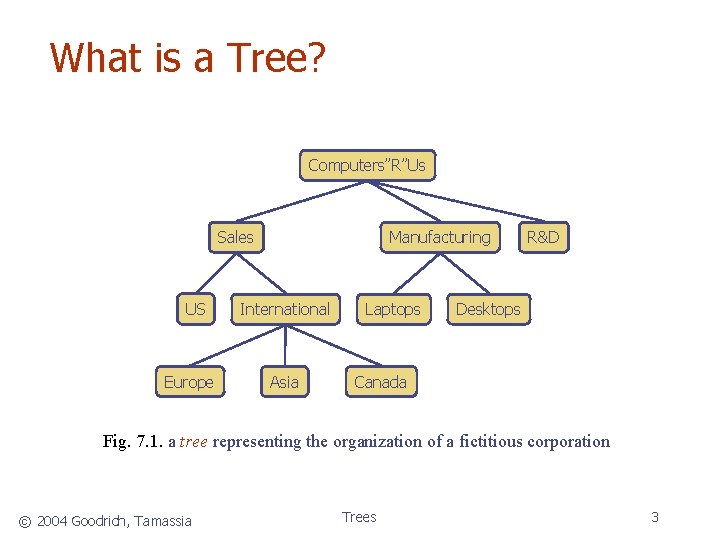
What is a Tree? Computers”R”Us Manufacturing Sales US Europe International Asia Laptops R&D Desktops Canada Fig. 7. 1. a tree representing the organization of a fictitious corporation © 2004 Goodrich, Tamassia Trees 3

Tree Structure In computer science, a tree is an abstract model of a hierarchical structure, with some objects being “above” and some “below” others. A tree consists of nodes with a parent-child relationship, rather than the simple “before” and “after” relationship, found between objects in sequential (linear ) structures. A famous example of hierarchical structure (tree) is the family tree. Applications: n n n Organization charts File systems Programming environments © 2004 Goodrich, Tamassia Trees 4

7. 1. 1 Tree Definitions and Properties A tree T, is an abstract data type that stores elements hierarchically. Except the top element (root), each element in a tree has a parent and zero or more children elements. root: node without parent (Node A) Internal node: node with at least one child (A, B, C, F) External node ( leaf ): node without children (E, I, J, K, G, H, D) Sibling nodes: Two nodes that are children of the same parent are Siblings. © 2004 Goodrich, Tamassia Trees Depth of a node: number of its ancestors Height of a tree: maximum depth of any node Ancestors of a node: parent, grand-grandparent, … etc. Descendants of a node: child, grandgrandchild, … etc. Subtree: a tree consisting of a node and its descendants 5

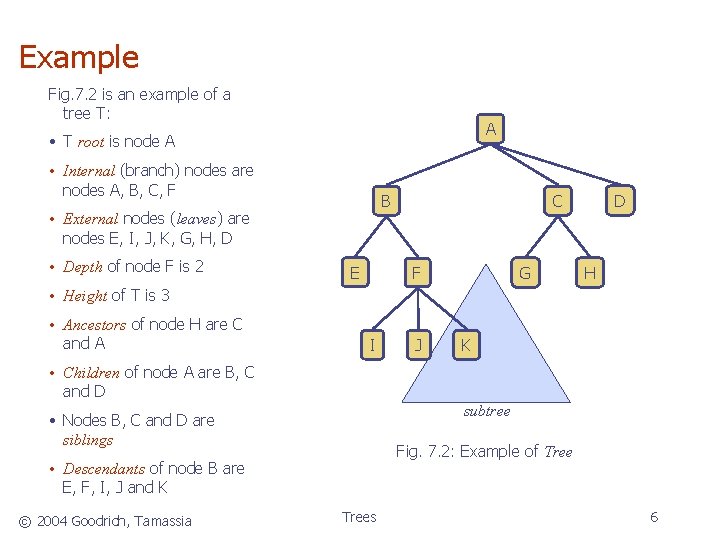
Example Fig. 7. 2 is an example of a tree T: A • T root is node A • Internal (branch) nodes are nodes A, B, C, F • External nodes (leaves) are nodes E, I, J, K, G, H, D • Depth of node F is 2 E D C B F G H • Height of T is 3 • Ancestors of node H are C and A I J K • Children of node A are B, C and D subtree • Nodes B, C and D are siblings Fig. 7. 2: Example of Tree • Descendants of node B are E, F, I, J and K © 2004 Goodrich, Tamassia Trees 6

Formal Definition of a Tree Formally, we define a tree T as a finite set of nodes storing elements such that the nodes have a parent-child relationship, that satisfies the following properties: n n n If T is nonempty, it has a specially designated node, called the root of T, that has no parent. Each node v of T other than the root has a unique parent node w. Every node with parent w is a child of w. Note that a tree may be empty. © 2004 Goodrich, Tamassia Trees 7

Recursive Definition of a Tree: A tree T is either empty, or has a finite set of one or more nodes such that: i. There is one specially designated node, called the root, and ii. The remaining nodes, (excluding the root), are partitioned into m ≥ 0 disjoint sets T 1 , T 2 , …, Tm, and each of these is in turn a tree. iii. The trees Ti (i = 1, 2, …, m) are called the sub-trees of the root. © 2004 Goodrich, Tamassia Trees 8

Subtree of Tree T The subtree of a tree T, rooted at node v is the tree consisting all the descendants of v in T (including v itself). Edges and Paths in Trees: n n n An edge of tree T is a pair of nodes (u, v), such that u is the parent of v, or vice versa. A path of T is a sequence of nodes such any two consecutive nodes in the sequence form an edge. As an example of a path, (Figure 7. 2), is the sequence A, B, F, K. where (A , B) or (B , A) is an edge. © 2004 Goodrich, Tamassia Trees 9

Ordered Trees A tree is ordered if there is a linear ordering defined for the children of each node; That’s, we can identify the children of a node as being the first, second, third, and so on. Such an ordering is usually shown by arranging siblings left to right, according to their ordering. Ordered trees typically indicate the linear order among siblings by listing them in the correct order. A famous example of ordered trees is the family tree. © 2004 Goodrich, Tamassia Trees 10

7. 1. 2 Tree ADT § The tree ADT stores elements at positions, which are defined relative to neighboring positions. § Positions in a tree are its nodes, and the neighboring positions satisfy the parent-child relationships that define a valid tree. § Tree nodes may store arbitrary objects. § As with a list position, a position object for a tree supports the method: element() : that returns the object stored at this position (or node). § The tree ADT supports four types of methods, as follows. © 2004 Goodrich, Tamassia Trees 11

Methods of a Tree ADT 1. Accessor Methods We use positions to abstract nodes. The real power of node positions in a tree comes from the accessor methods of the tree ADT that return and accept positions, such as the following: n root(): Return the position of the tree’s root; an error occurs if the tree is empty. n parent(p): Return the position of the parent of p; an error occurs if p is the root. n children(p): Return an iterable collection containing the children of node p. © 2004 Goodrich, Tamassia Trees 12

Notice that: § If a tree T is ordered, then the iterable collection, children(p), stores the children of p in their linear order. § If p is an external node, then children(p) is empty. § Any method that takes a position as argument should generate an error condition if that position is invalid. © 2004 Goodrich, Tamassia Trees 13

Methods of a Tree ADT (Cont. ) 2. Generic methods n n size(): Return the number of nodes in the tree. is. Empty(): Test whether the tree has any nodes or not. Iterator(): Return an iterator of all the elements stored at nodes of the tree. positions(): Return an iterable collection of all the nodes of the tree. © 2004 Goodrich, Tamassia Trees 14

Methods of a Tree ADT (Cont. ) 3. Query methods In addition to the above fundamental accessor methods, the tree ADT also supports the following Boolean query methods: is. Internal(p): Test whether node p is an internal node n is. External(p): Test whether node p is an external node 3. is. Root(p): Test whether node p is the root node These methods make programming with tree easier and more n readable, since we can use them in the conditionals of if statements and while -loops, rather than using a non-intuitive conditional. © 2004 Goodrich, Tamassia Trees 15

Methods of a Tree ADT (Cont. ) 4. Update Method The tree ADT also supports the following update method: n replace(p, e): Replace with e and return the element stored at node p. Additional update methods may be defined by data structures implementing the © 2004 Goodrich, Tamassia Trees tree ADT 16

Tree ADT Exceptions An interface for the tree ADT uses the following exceptions to indicate error conditions: § Invalid. Position. Exception: This error condition may be thrown by any method taking a position as an argument to indicate that the position is invalid. § Boundary. Violation. Exception: This error condition may be thrown by method parent() if it’s called on the root. § Empty. Tree. Exception: This error condition may be thrown by method root() if it’s called on an empty tree. © 2004 Goodrich, Tamassia Trees 17

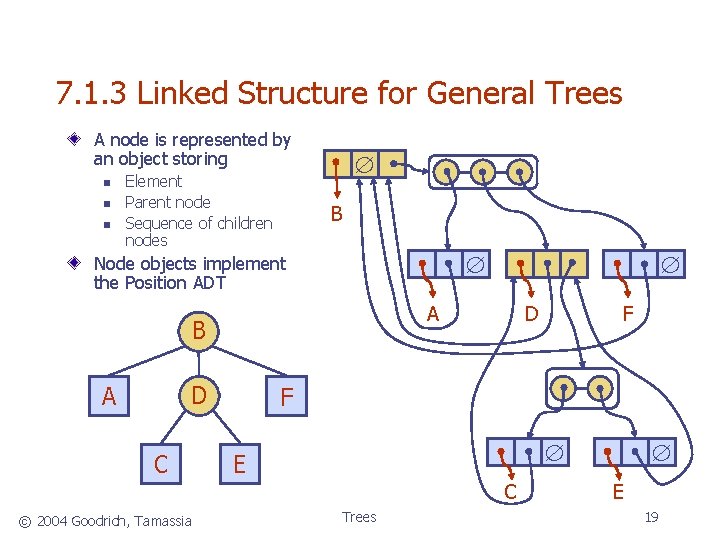
7. 1. 3 A Linked Structure for General Trees A natural way to implement a tree T is to use a linked structure, where we represent each node p of T by a position object with the following fields (see Figure): A reference to the element stored at p. A link to the parent of p. A some kind of collection (e. g. , a list or array) to store links to the children of p. © 2004 Goodrich, Tamassia Trees 18

7. 1. 3 Linked Structure for General Trees A node is represented by an object storing n n n Element Parent node Sequence of children nodes B Node objects implement the Position ADT A B D A C D F E C © 2004 Goodrich, Tamassia F Trees E 19

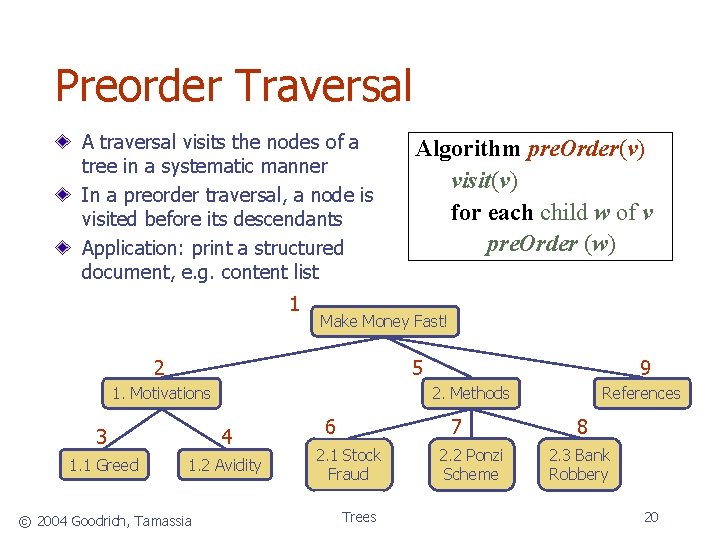
Preorder Traversal A traversal visits the nodes of a tree in a systematic manner In a preorder traversal, a node is visited before its descendants Application: print a structured document, e. g. content list 1 Algorithm pre. Order(v) visit(v) for each child w of v pre. Order (w) Make Money Fast! 2 5 1. Motivations 2. Methods 3 4 1. 1 Greed 1. 2 Avidity © 2004 Goodrich, Tamassia 9 6 7 2. 1 Stock Fraud Trees 2. 2 Ponzi Scheme References 8 2. 3 Bank Robbery 20

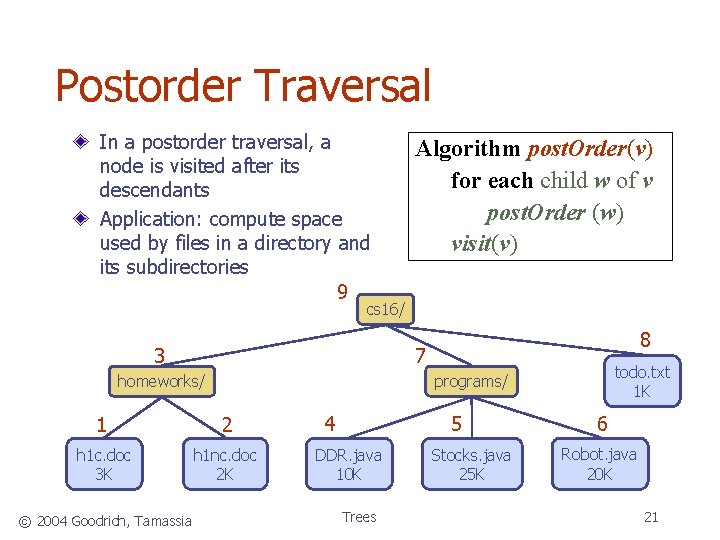
Postorder Traversal In a postorder traversal, a node is visited after its descendants Application: compute space used by files in a directory and its subdirectories 9 Algorithm post. Order(v) for each child w of v post. Order (w) visit(v) cs 16/ 3 7 homeworks/ todo. txt 1 K programs/ 1 2 h 1 c. doc 3 K h 1 nc. doc 2 K © 2004 Goodrich, Tamassia 8 4 5 DDR. java 10 K Trees Stocks. java 25 K 6 Robot. java 20 K 21

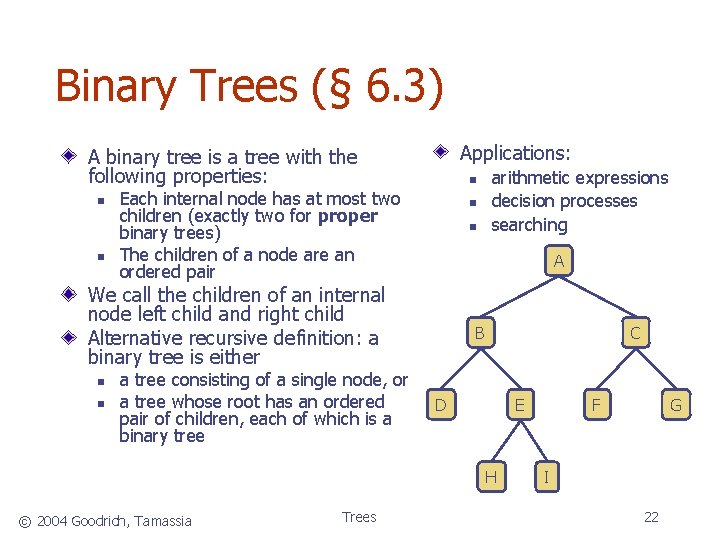
Binary Trees (§ 6. 3) Applications: A binary tree is a tree with the following properties: n n n Each internal node has at most two children (exactly two for proper binary trees) The children of a node are an ordered pair n n A We call the children of an internal node left child and right child Alternative recursive definition: a binary tree is either n n a tree consisting of a single node, or a tree whose root has an ordered pair of children, each of which is a binary tree arithmetic expressions decision processes searching B C D H © 2004 Goodrich, Tamassia Trees F E G I 22

Arithmetic Expression Tree Binary tree associated with an arithmetic expression n n internal nodes: operators external nodes: operands Example: arithmetic expression tree for the expression (2 (a - 1) + (3 b)) + - 2 a © 2004 Goodrich, Tamassia 3 b 1 Trees 23

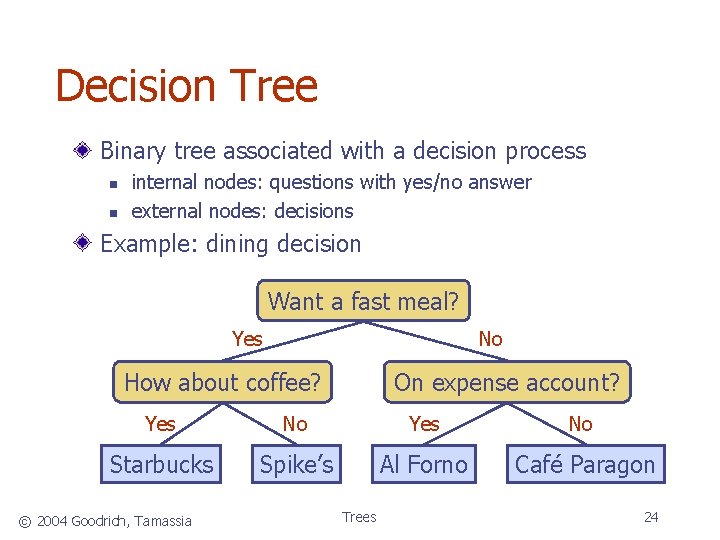
Decision Tree Binary tree associated with a decision process n n internal nodes: questions with yes/no answer external nodes: decisions Example: dining decision Want a fast meal? No Yes How about coffee? On expense account? Yes No Starbucks Spike’s Al Forno Café Paragon © 2004 Goodrich, Tamassia Trees 24

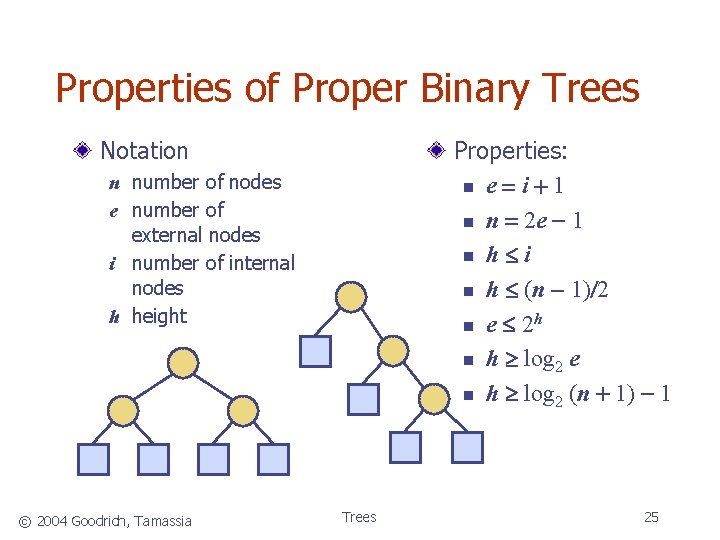
Properties of Proper Binary Trees Notation Properties: n e = i + 1 n n = 2 e - 1 n h i n h (n - 1)/2 n e 2 h n h log 2 e n h log 2 (n + 1) - 1 n number of nodes e number of external nodes i number of internal nodes h height © 2004 Goodrich, Tamassia Trees 25

Binary. Tree ADT (§ 6. 3. 1) The Binary. Tree ADT extends the Tree ADT, i. e. , it inherits all the methods of the Tree ADT Additional methods: n n Update methods may be defined by data structures implementing the Binary. Tree ADT position left(p) position right(p) boolean has. Left(p) boolean has. Right(p) © 2004 Goodrich, Tamassia Trees 26

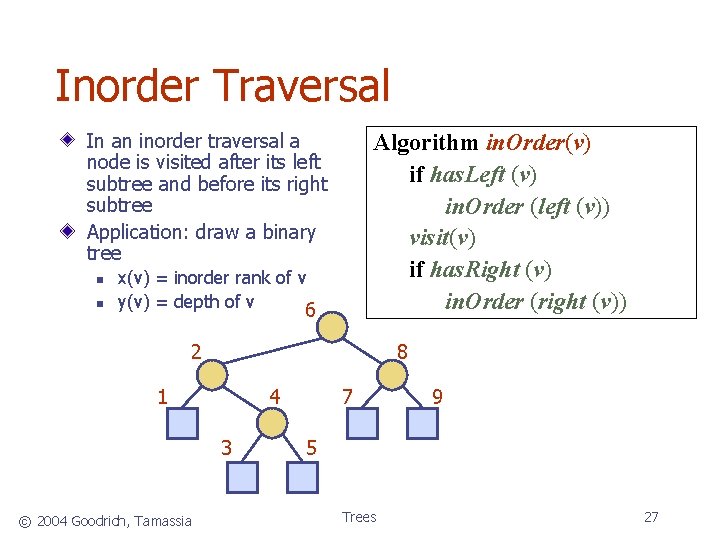
Inorder Traversal In an inorder traversal a node is visited after its left subtree and before its right subtree Application: draw a binary tree n n Algorithm in. Order(v) if has. Left (v) in. Order (left (v)) visit(v) if has. Right (v) in. Order (right (v)) x(v) = inorder rank of v y(v) = depth of v 6 2 8 1 4 3 © 2004 Goodrich, Tamassia 7 9 5 Trees 27

Print Arithmetic Expressions Specialization of an inorder traversal n n n print operand or operator when visiting node print “(“ before traversing left subtree print “)“ after traversing right subtree + - 2 a 3 Algorithm print. Expression(v) if has. Left (v) print(“(’’) in. Order (left(v)) print(v. element ()) if has. Right (v) in. Order (right(v)) print (“)’’) b ((2 (a - 1)) + (3 b)) 1 © 2004 Goodrich, Tamassia Trees 28

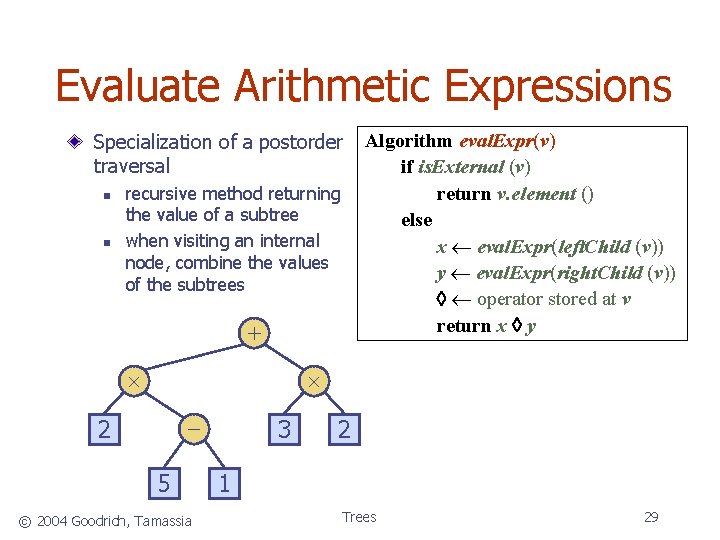
Evaluate Arithmetic Expressions Specialization of a postorder traversal n n recursive method returning the value of a subtree when visiting an internal node, combine the values of the subtrees + Algorithm eval. Expr(v) if is. External (v) return v. element () else x eval. Expr(left. Child (v)) y eval. Expr(right. Child (v)) operator stored at v return x y - 2 5 © 2004 Goodrich, Tamassia 3 2 1 Trees 29

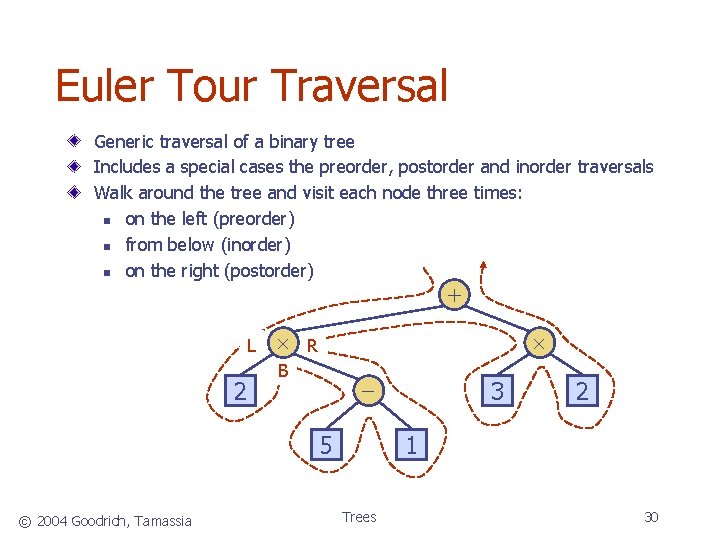
Euler Tour Traversal Generic traversal of a binary tree Includes a special cases the preorder, postorder and inorder traversals Walk around the tree and visit each node three times: n on the left (preorder) n from below (inorder) n on the right (postorder) + L 2 R B 5 © 2004 Goodrich, Tamassia 3 2 1 Trees 30

Template Method Pattern Generic algorithm that can be specialized by redefining certain steps Implemented by means of an abstract Java class Visit methods that can be redefined by subclasses Template method euler. Tour public abstract class Euler. Tour { protected Binary. Tree tree; protected void visit. External(Position p, Result r) { } protected void visit. Left(Position p, Result r) { } protected void visit. Below(Position p, Result r) { } protected void visit. Right(Position p, Result r) { } protected Object euler. Tour(Position p) { n Recursively called on the Result r = new Result(); left and right children if tree. is. External(p) { visit. External(p, r); } n A Result object with else { fields left. Result, visit. Left(p, r); right. Result and r. left. Result = euler. Tour(tree. left(p)); final. Result keeps track of visit. Below(p, r); the output of the r. right. Result = recursive calls to euler. Tour(tree. right(p)); euler. Tour Trees 31 © 2004 Goodrich, Tamassia visit. Right(p, r);

Specializations of Euler. Tour We show to specialize class Euler. Tour to evaluate an arithmetic expression Assumptions n n External nodes store Integer objects Internal nodes store Operator objects supporting method operation (Integer, Integer) public class Evaluate. Expression extends Euler. Tour { protected void visit. External(Position p, Result r) { r. final. Result = (Integer) p. element(); } protected void visit. Right(Position p, Result r) { Operator op = (Operator) p. element(); r. final. Result = op. operation( (Integer) r. left. Result, (Integer) r. right. Result ); } … © 2004 Goodrich, Tamassia } Trees 32

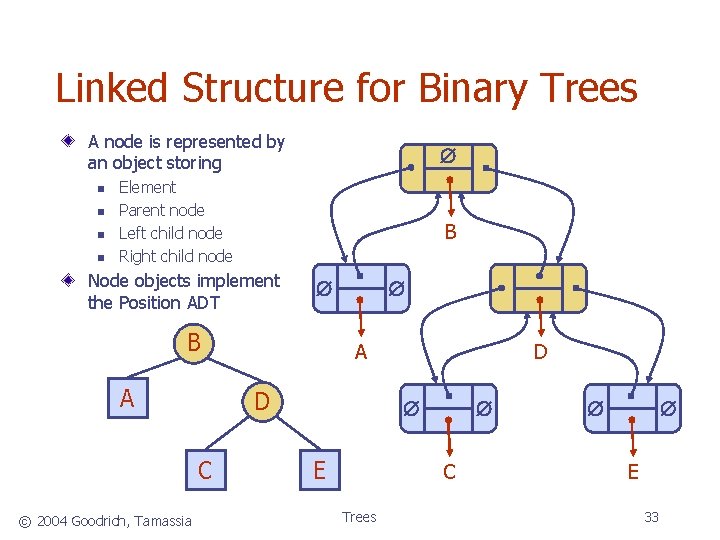
Linked Structure for Binary Trees A node is represented by an object storing n n Element Parent node Left child node Right child node B Node objects implement the Position ADT B A A D C © 2004 Goodrich, Tamassia D E C Trees E 33

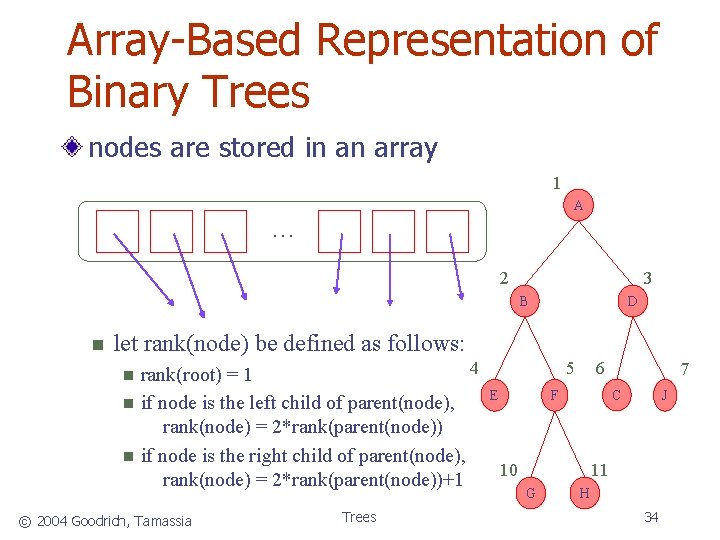
Array-Based Representation of Binary Trees nodes are stored in an array 1 A … 2 3 B n D let rank(node) be defined as follows: n n n 4 rank(root) = 1 if node is the left child of parent(node), rank(node) = 2*rank(parent(node)) if node is the right child of parent(node), rank(node) = 2*rank(parent(node))+1 © 2004 Goodrich, Tamassia Trees 5 E 6 7 C F 10 J 11 G H 34
 How do fraud symptoms help in detecting fraud
How do fraud symptoms help in detecting fraud Dana damian
Dana damian Example of acid-fast bacteria
Example of acid-fast bacteria Example of acid-fast bacteria
Example of acid-fast bacteria Features of preferred stock
Features of preferred stock Teknik pembuatan white stock sesuai dengan standar
Teknik pembuatan white stock sesuai dengan standar Characteristics of common shares
Characteristics of common shares Stock final de marchandises
Stock final de marchandises Old money
Old money Money smart money match
Money smart money match Money on money multiple
Money on money multiple Old money vs new money
Old money vs new money Tom buchanan character traits
Tom buchanan character traits Chapter 3 ethics fraud and internal control
Chapter 3 ethics fraud and internal control Chapter 7 fraud internal control and cash
Chapter 7 fraud internal control and cash Chapter 7 fraud internal control and cash
Chapter 7 fraud internal control and cash Imprest system
Imprest system Make the common case fast
Make the common case fast Make to stock
Make to stock Dynamics 365 lean manufacturing
Dynamics 365 lean manufacturing How do banks make money?
How do banks make money? Jay gould childhood
Jay gould childhood Make your money grow
Make your money grow Money make the world go round meaning
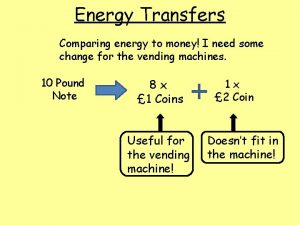
Money make the world go round meaning Make an analogy comparing energy and money
Make an analogy comparing energy and money How to make money using machine learning
How to make money using machine learning Make the lie big, make it simple
Make the lie big, make it simple Go make a difference
Go make a difference Make the lie big, make it simple
Make the lie big, make it simple Define headright system
Define headright system Fraud and abuse management system
Fraud and abuse management system Sfcu medford
Sfcu medford Risk assessment fraud
Risk assessment fraud Fraud and abuse module
Fraud and abuse module Saul kripke
Saul kripke