Chapter 7 Non Linear Data Structure www asyrani

Chapter 7 Non Linear Data Structure www. asyrani. com

Linear – Data is in sequential Non Linear – Data is not in sequential

Data Structure Linear – In Sequence Non Linear – Not in sequence • Insertion/Deletion is possible in linear(sequential) fashion • Example: • Insertion/Deletion is not possible • Example: – – Array Stacks Queues Linked List – Graphs – Trees – Hash Tree

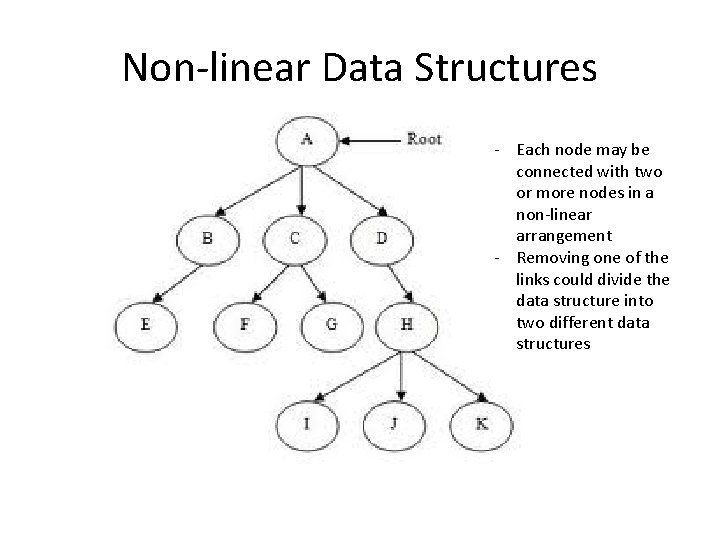
Non-linear Data Structures - Each node may be connected with two or more nodes in a non-linear arrangement - Removing one of the links could divide the data structure into two different data structures

EXAMPLE OF NON-LINEAR DS

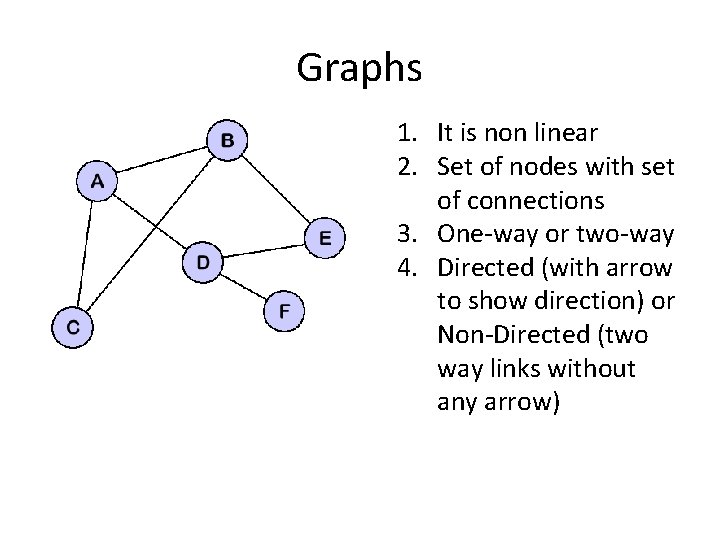
Graphs 1. It is non linear 2. Set of nodes with set of connections 3. One-way or two-way 4. Directed (with arrow to show direction) or Non-Directed (two way links without any arrow)

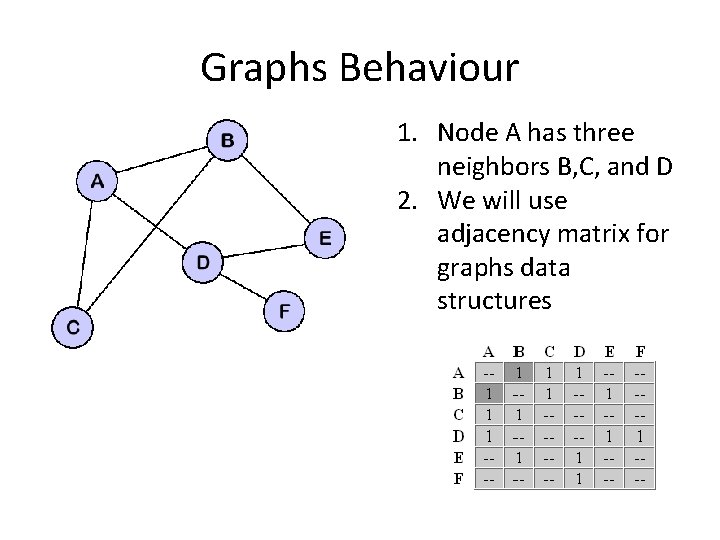
Graphs Behaviour 1. Node A has three neighbors B, C, and D 2. We will use adjacency matrix for graphs data structures

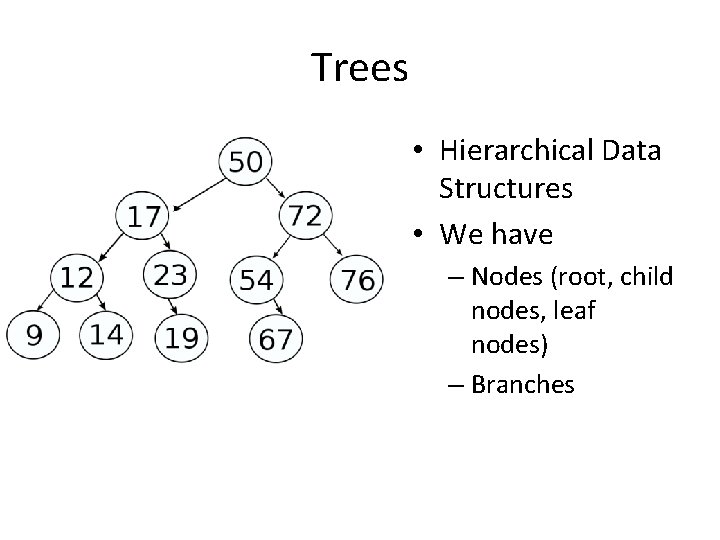
Trees • Hierarchical Data Structures • We have – Nodes (root, child nodes, leaf nodes) – Branches

TREES – TERMINOLOGY – TRAVERSAL – TYPE OF TREES

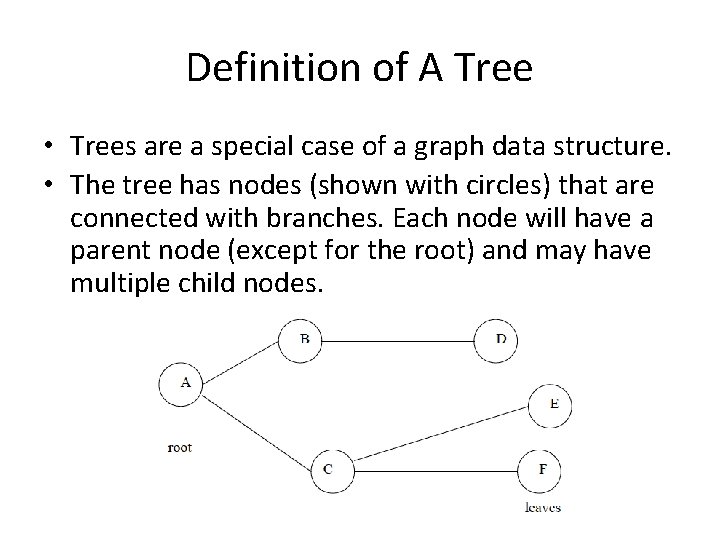
Definition of A Tree • Trees are a special case of a graph data structure. • The tree has nodes (shown with circles) that are connected with branches. Each node will have a parent node (except for the root) and may have multiple child nodes.

“Trees” in real application

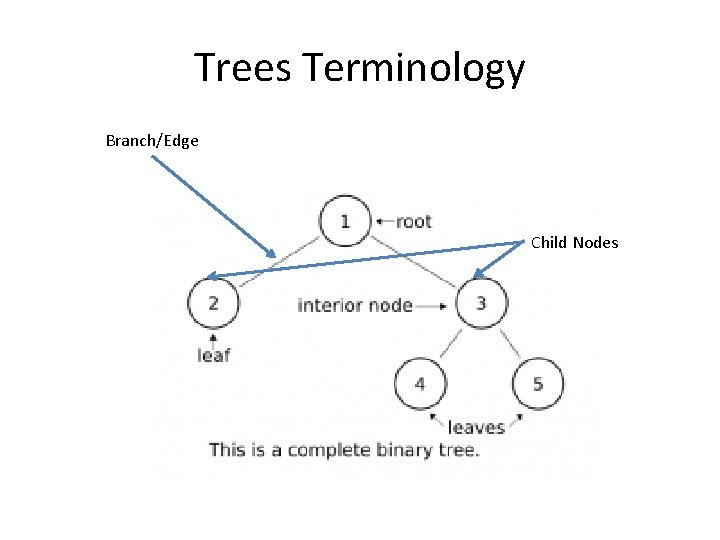
Trees Terminology Branch/Edge Child Nodes

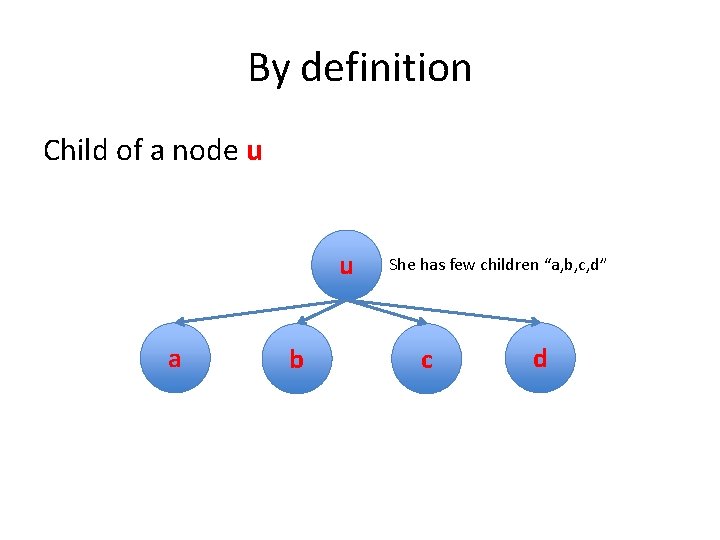
By definition Child of a node u u a b She has few children “a, b, c, d” c d

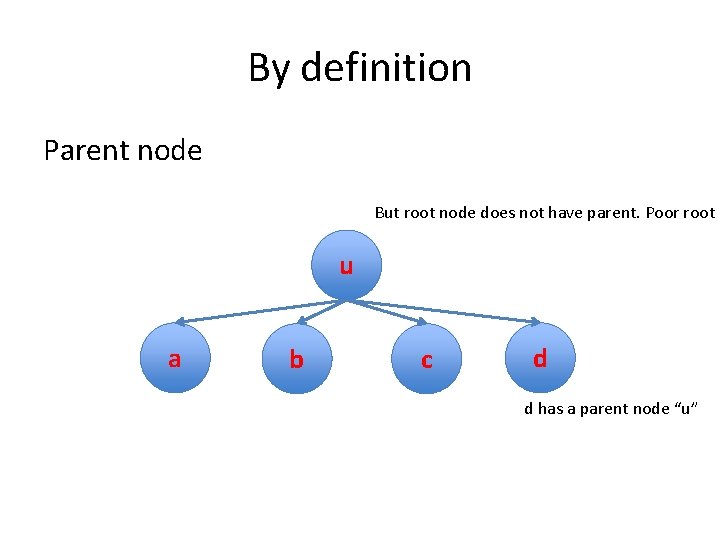
By definition Parent node But root node does not have parent. Poor root u a b c d d has a parent node “u”

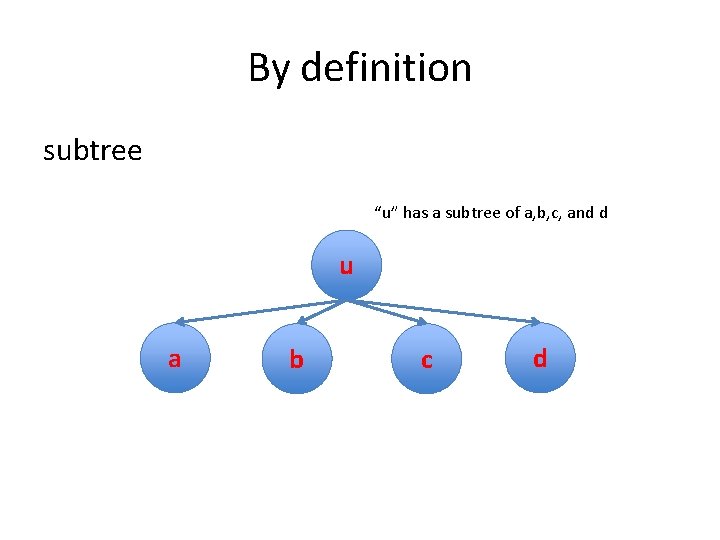
By definition subtree “u” has a subtree of a, b, c, and d u a b c d

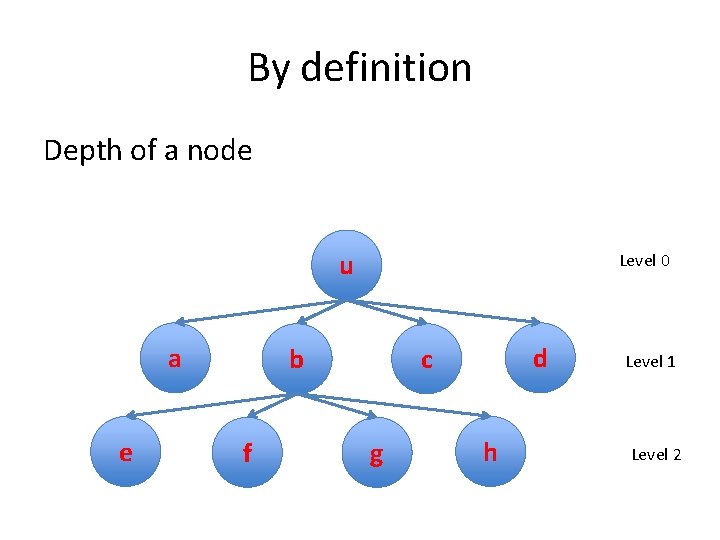
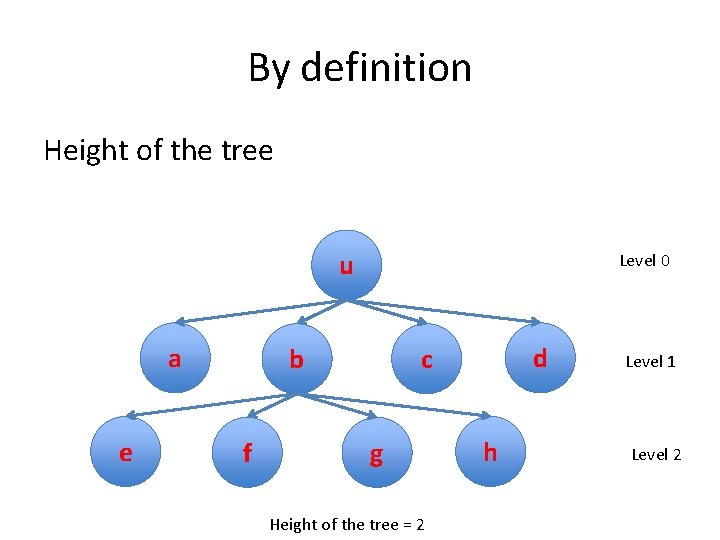
By definition Depth of a node u a e Level 0 b f d c g h Level 1 Level 2

By definition Height of the tree u a e Level 0 b f d c g Height of the tree = 2 h Level 1 Level 2

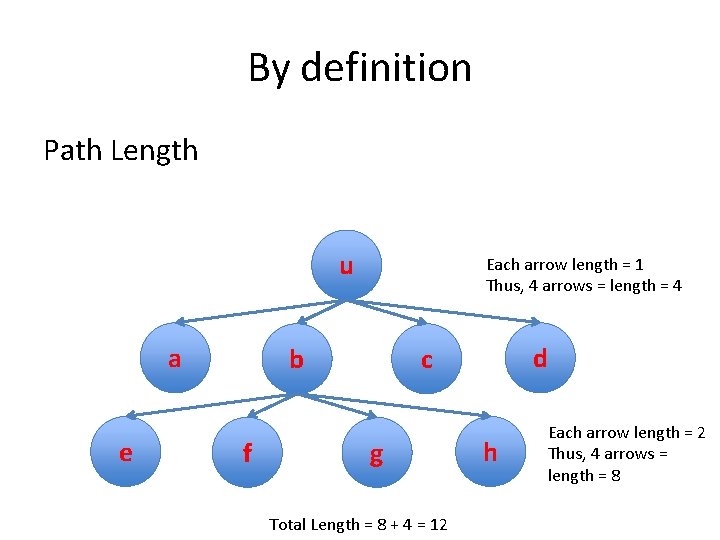
By definition Path Length u a e Each arrow length = 1 Thus, 4 arrows = length = 4 b f d c g Total Length = 8 + 4 = 12 h Each arrow length = 2 Thus, 4 arrows = length = 8

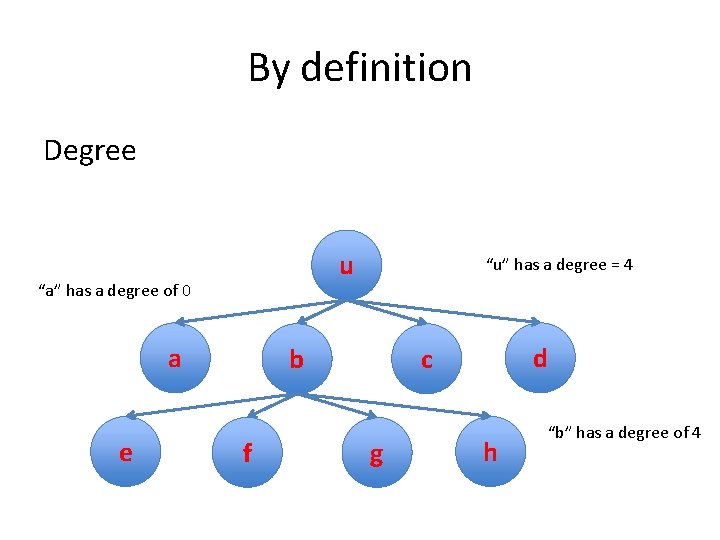
By definition Degree u “a” has a degree of 0 a e “u” has a degree = 4 b f d c g h “b” has a degree of 4

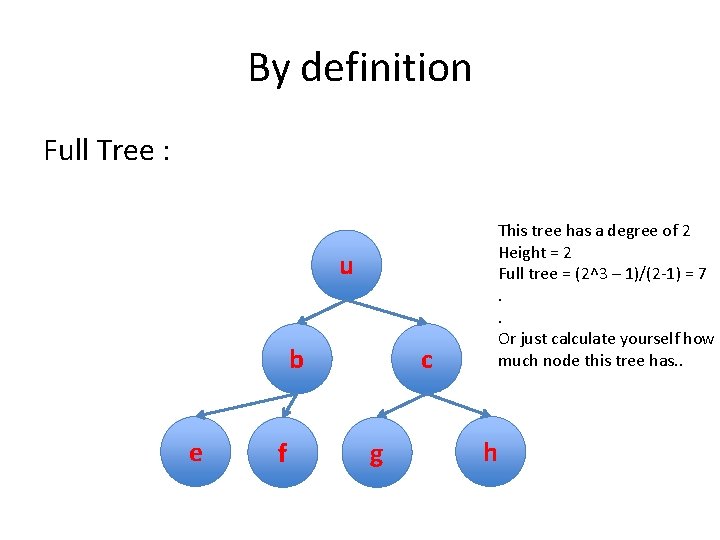
By definition Full Tree : u b e f c g This tree has a degree of 2 Height = 2 Full tree = (2^3 – 1)/(2 -1) = 7. . Or just calculate yourself how much node this tree has. . h

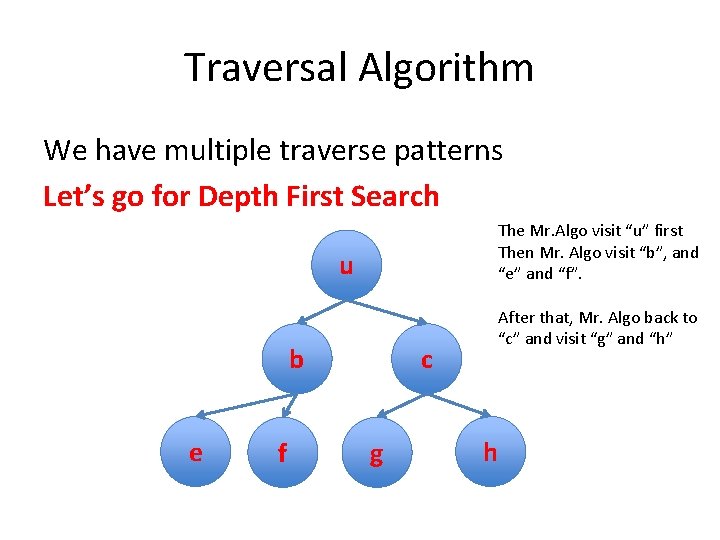
Traversal Algorithm We have multiple traverse patterns Let’s go for Depth First Search The Mr. Algo visit “u” first Then Mr. Algo visit “b”, and “e” and “f”. u b e f c g After that, Mr. Algo back to “c” and visit “g” and “h” h

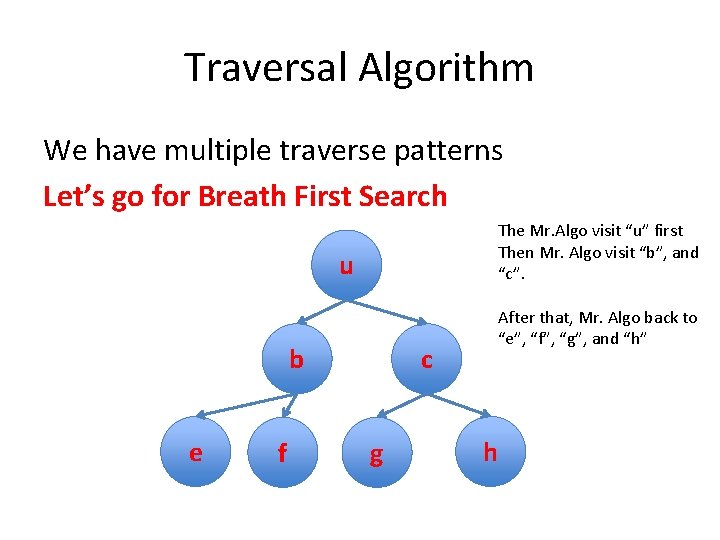
Traversal Algorithm We have multiple traverse patterns Let’s go for Breath First Search The Mr. Algo visit “u” first Then Mr. Algo visit “b”, and “c”. u b e f c g After that, Mr. Algo back to “e”, “f”, “g”, and “h” h

Rooted Tree/Ordered Tree Rooted Tree Ordered Tree • Any node can become a root for its own subnode • General term “Free Tree” • They have more family tree definition such as siblings or grandparents. • Rooted tree where order of each child node is specified. [English] It is where you determined yourself where you put your node. • But if we have spesific order, then we could have so called n-tree (binary, quad, oct-tree)

BINARY TREE

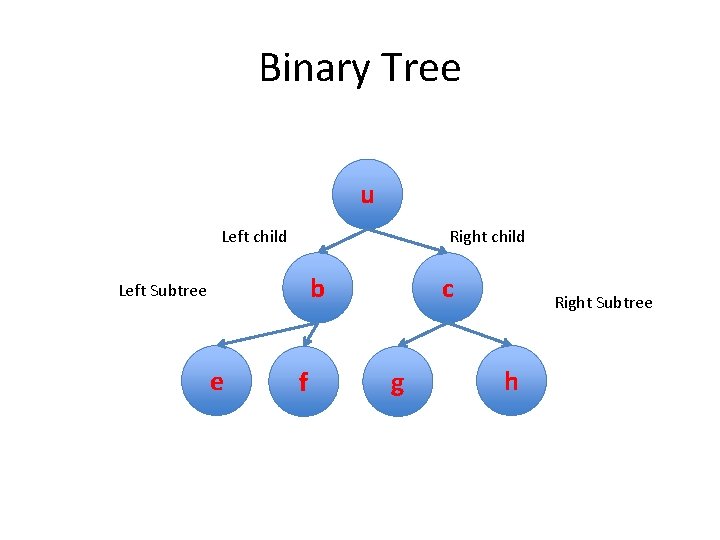
Binary Tree u Left child Right child b Left Subtree e f c g Right Subtree h

Binary Tree : Code struct Tree. Node { int item; //The data in this node. Tree. Node *left; //Pointer to the left subtree. Tree. Node *right; //Pointer to the right subtree. }

Binary Tree : Code int count. Nodes( Tree. Node *root ) { // Count the nodes in the binary tree to which // root points, and return the answer. if ( root == NULL ) return 0; // The tree is empty. It contains no nodes. else { int count = 1; // Start by counting the root. count += count. Nodes(root->left); // Add the number of nodes // in the left subtree. count += count. Nodes(root->right); // Add the number of nodes // in the right subtree. return count; // Return the total. } } // end count. Nodes()

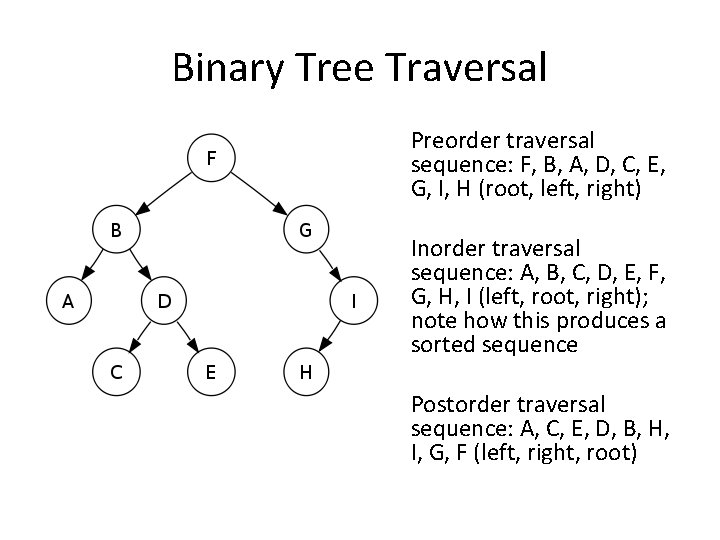
Binary Tree Traversal Preorder traversal sequence: F, B, A, D, C, E, G, I, H (root, left, right) Inorder traversal sequence: A, B, C, D, E, F, G, H, I (left, root, right); note how this produces a sorted sequence Postorder traversal sequence: A, C, E, D, B, H, I, G, F (left, right, root)

DELETE A NODE

DELETE A NODE IN TREE There are three possible cases to consider: • Deleting a leaf (node with no children): Deleting a leaf is easy, as we can simply remove it from the tree. • Deleting a node with one child: Remove the node and replace it with its child. • Deleting a node with two children: Call the node to be deleted N. Do not delete N. Instead, choose either its in-order successor node or its in-order predecessor node, R. Replace the value of N with the value of R, then delete R.

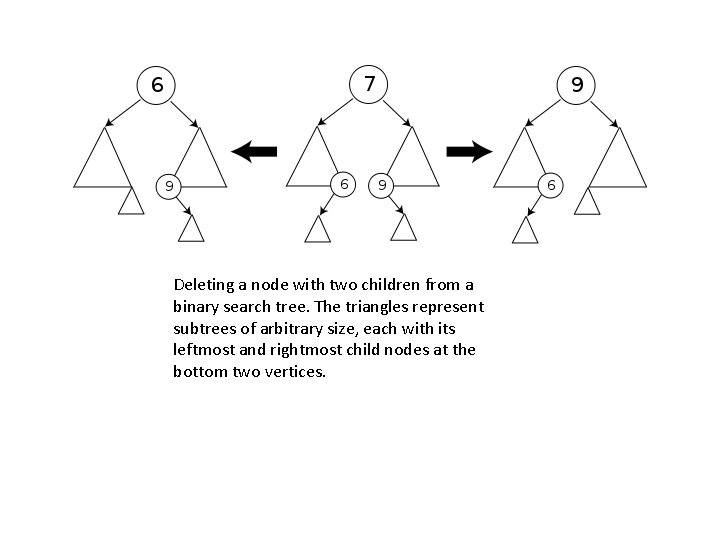
Deleting a node with two children from a binary search tree. The triangles represent subtrees of arbitrary size, each with its leftmost and rightmost child nodes at the bottom two vertices.

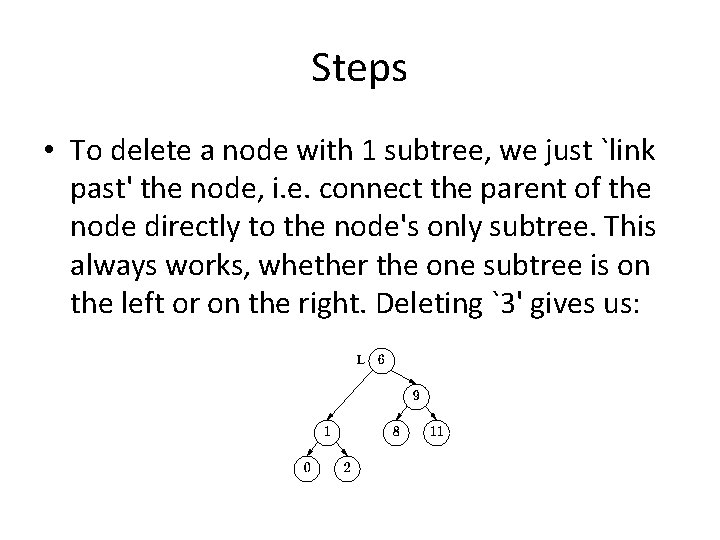
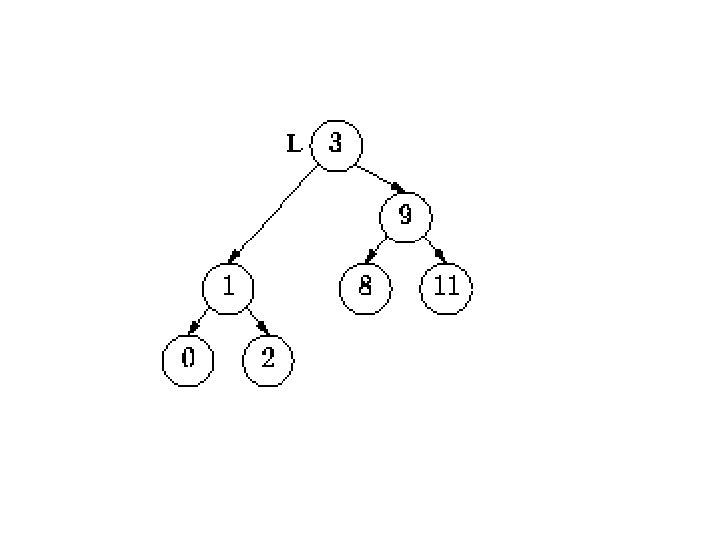
Steps • There is another simple situation: suppose the node we're deleting has only one subtree. In the following example, `3' has only 1 subtree.

Steps • To delete a node with 1 subtree, we just `link past' the node, i. e. connect the parent of the node directly to the node's only subtree. This always works, whether the one subtree is on the left or on the right. Deleting `3' gives us:

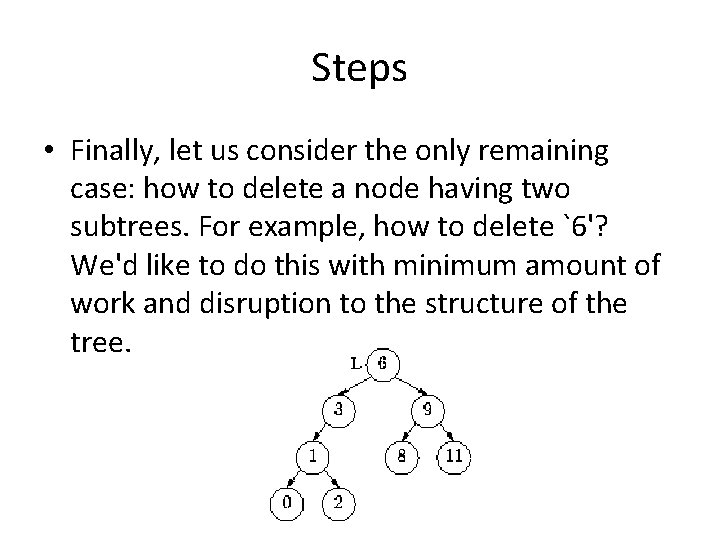
Steps • Finally, let us consider the only remaining case: how to delete a node having two subtrees. For example, how to delete `6'? We'd like to do this with minimum amount of work and disruption to the structure of the tree.

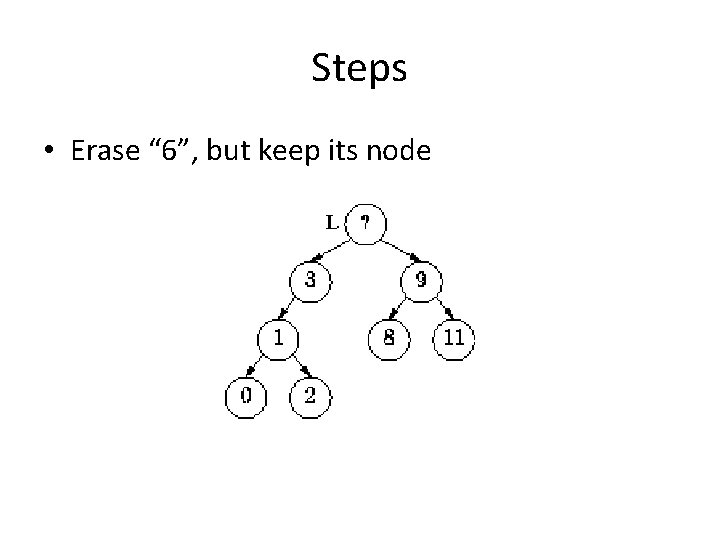
Steps • Erase “ 6”, but keep its node

Steps • Find value that can be moved into vacated node while preserving BST properties. Pick X such that: – everything in left subtree < X – everything in right subtree > X • If we get X from left subtree, (2) is guaranteed. – For (1), X must be largest value in left subtree, i. e. 3.

Steps • General algorithm: to delete N, if it has 2 subtrees, replace the value in N with the largest value in its left subtree and then delete the node with the largest value from its left subtree. • Note: the largest value has at most one subtree. • Why? It is the largest value: it doesn't have a right subtree.

Let’s run sample program • Start your Visual Studio 2010 now • Create new C++ empty project • Project : Binary Tree with Traversal of DFS