Chapter 3 Gatelevel Minimization 1 Simplification Using Prime

Chapter 3 Gate-level Minimization 1

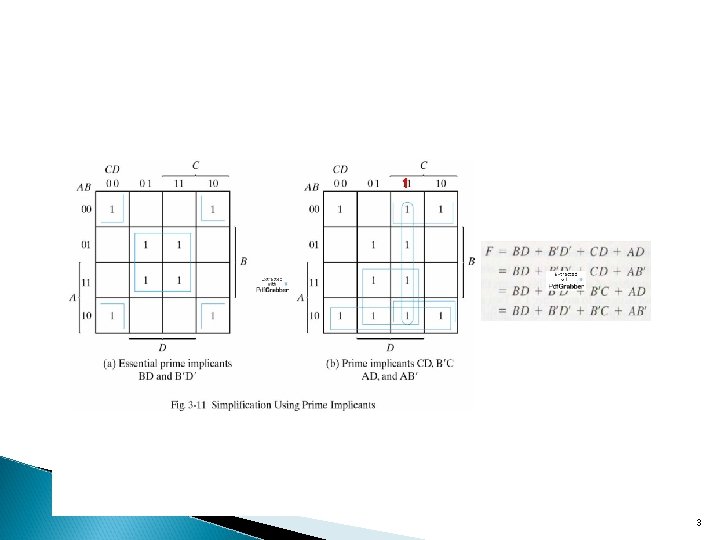
Simplification Using Prime Implicants § A Prime Implicant is a product term obtained by combining the maximum possible number of adjacent squares in the map into a rectangle with the number of squares a power of 2. § A prime implicant is called an Essential Prime Implicant if it is the only prime implicant that covers (includes) one or more minterms. § Prime Implicants and Essential Prime Implicants can be determined by inspection of a K-Map. 2

1 3

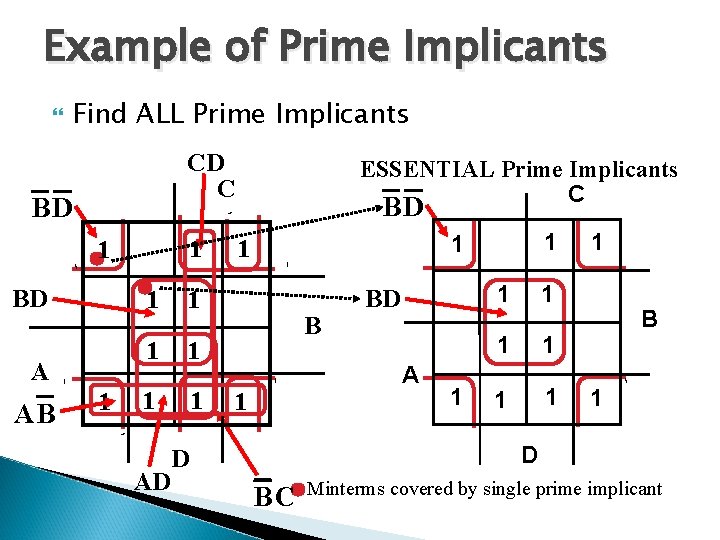
Example of Prime Implicants Find ALL Prime Implicants CD C BD 1 1 BD A AB 1 1 1 1 D AD ESSENTIAL Prime Implicants C BD 1 1 1 BD 1 B A 1 1 1 1 D BC Minterms covered by single prime implicant

Prime Implicant Practice Find all prime implicants for: F (W, X, Y, Z) = (0, 2, 3, 8, 9, 10, 11, 12, 13, 14, 15) Y 1 1 W 1 1 1 1 1 X Z Prime implicants are: W, X‘Y, and X‘Z‘ Note that all of these prime implicants are essential.

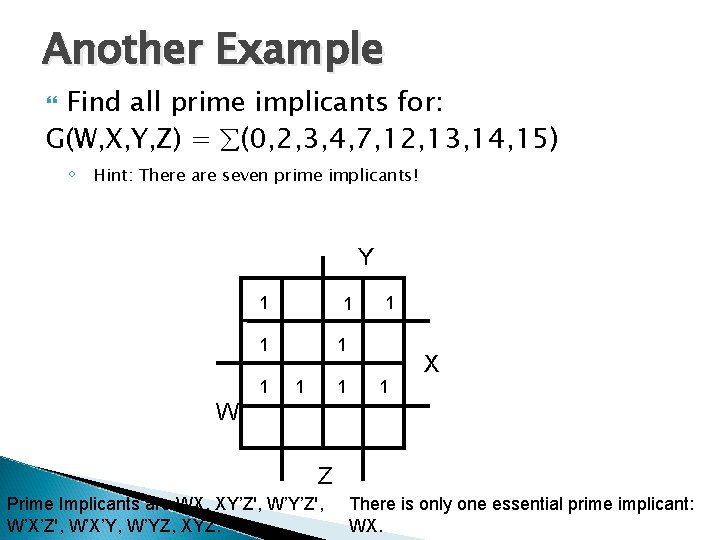
Another Example Find all prime implicants for: G(W, X, Y, Z) = (0, 2, 3, 4, 7, 12, 13, 14, 15) ◦ Hint: There are seven prime implicants! Y 1 1 1 1 1 X W Z Prime Implicants are WX, XY’Z', W’X’Z', W’X’Y, W’YZ, XYZ. There is only one essential prime implicant: WX.

3 -4 Five-Variable Map 7

8

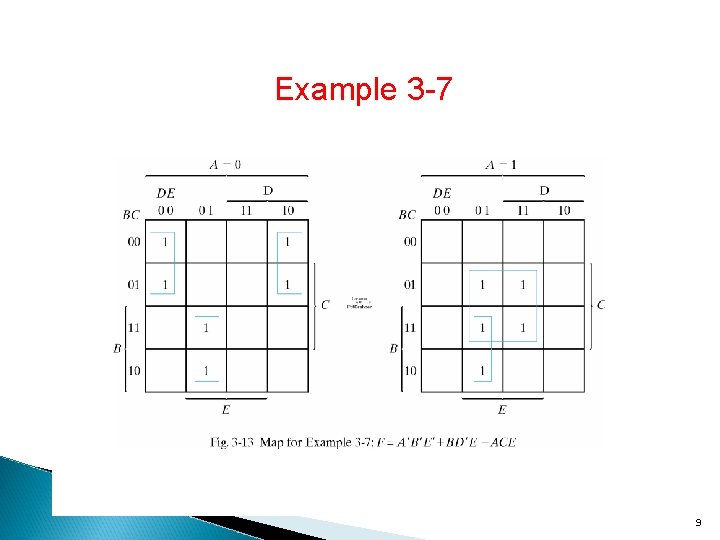
Example 3 -7 9

3 -5 Product-of-Sums Simplification E. g. Simplify the following Boolean function in product-of -sums form F(A, B, C, D)= m(0, 1, 2, 5, 8, 9, 10) 1. 2. 3. 4. Mark with 1’s the minterms of F. Mark the remaining squares with 0’s. These represent F’. Find the simplified F’. F’ = AB + CD + BD’ Complement 3 to obtain a simplified F in product-ofsums form F = (A’ + B’)(C’ + D’) (B’ +D)

Product-of-Sums Simplification Simplify : F= (0, 1, 2, 5, 8, 9, 10) in Product-of-Sums Form 1. Mark with 0’s the Maxterms of F 2. Combine 0’s to obtain a simplified F’ in SOP. A 3. Complement 2 to obtain a simplified F in POS. F’ = AB + CD + BD’ F = (A’+B’)(C’+D’)(B’+D) C B D

Example 3 -8 Simply Boolean function F(A, B, C, D) = (0, 1, 2, 5, 8, 9, 10) in (a) sum of products and (b) product of sums (a) F = B’D’ + B’C‘ + A’C’D (b) 1. Obtain simplified complemented function: F’ = AB + CD+BD’ 2. Applying De. Morgan’s theorem to obtain F F = (A’ + B’) (C’+D’) (B’ + D) 12

Gate Implementation for Example 3 -8 13

3. 6 Don't Cares Condition Sometimes a function table or map contains entries for which it is known: ◦ the input values for the minterm will never occur, or ◦ The output value for the minterm is not used In these cases, the output value need not be defined Instead, the output value is defined as a “don't care” By placing “don't cares” ( an “x” entry) in the function table or map, the cost of the logic circuit may be lowered. Example 1: A logic function having the binary codes for the BCD digits as its inputs. Only the codes for 0 through 9 are used. The six codes, 1010 through 1111 never occur, so the output

Example 3 -9 product of sums? 16