CS 105 DIGITAL LOGIC DESIGN GateLevel Minimization Chapter

CS 105 DIGITAL LOGIC DESIGN Gate-Level Minimization Chapter 3

Outline 3. 1 Introduction 3. 2 The Map Method 3. 3 Four-Variable Map 3. 4 Product of sums simplification 3. 6 Don‘t Care Conditions 3. 7 NAND and NOR Implementaion 3. 8 Other Two-Level Implementaion 3. 9 Exclusive-OR function

3. 1 Introduction (1 -1) Gate-Level Minimization Notes about simplification of Boolean expression Simplification Methods: q Algebraic minimization q Karnaugh map or K-map.

3. 2 The Map Method (1 -12) A Karnaugh map is a graphical tool for assisting in the general simplification procedure. Combination of 2, 4, … 2 n adjacent squares Canonical form: ( sum of minterms , product of maxterms. Standard form: ( simplifier : sum of product , product of sum

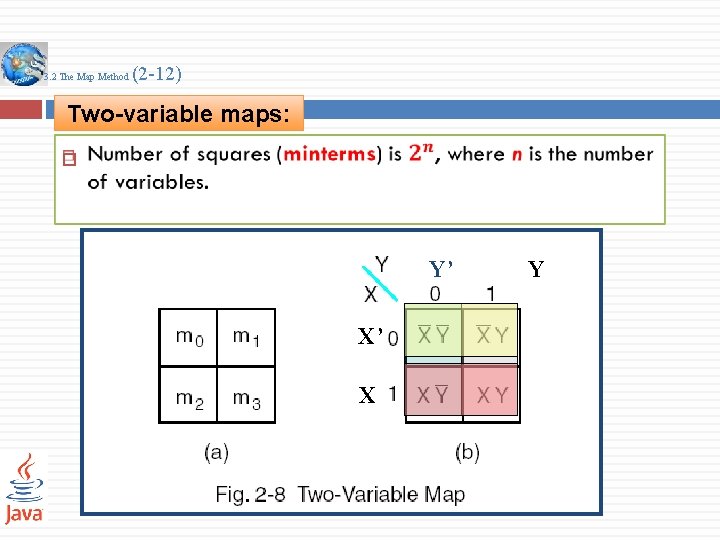
3. 2 The Map Method (2 -12) Two-variable maps: Y’ X’ X Y

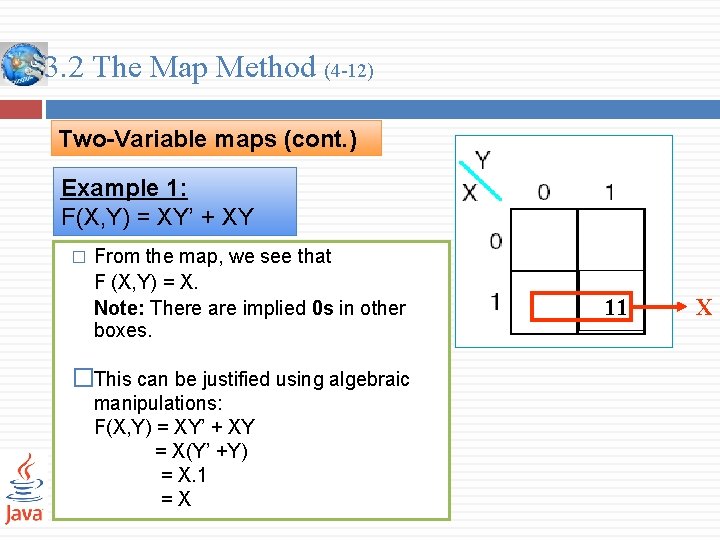
3. 2 The Map Method (4 -12) Two-Variable maps (cont. ) Example 1: F(X, Y) = XY’ + XY � From the map, we see that F (X, Y) = X. Note: There are implied 0 s in other boxes. �This can be justified using algebraic manipulations: F(X, Y) = XY’ + XY = X(Y’ +Y) = X. 1 =X 11 X

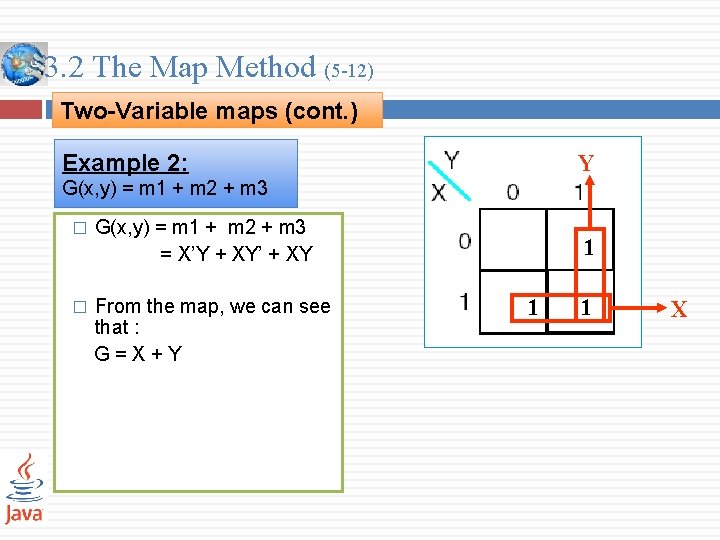
3. 2 The Map Method (5 -12) Two-Variable maps (cont. ) Example 2: Y G(x, y) = m 1 + m 2 + m 3 � G(x, y) = m 1 + m 2 + m 3 = X’Y + XY’ + XY � From the map, we can see that : G=X+Y 1 1 1 X

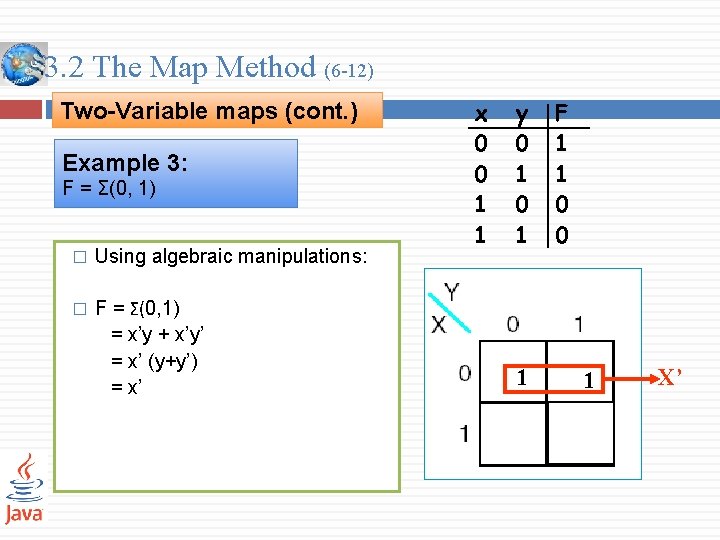
3. 2 The Map Method (6 -12) Two-Variable maps (cont. ) Example 3: F = Σ(0, 1) � Using algebraic manipulations: � F = Σ(0, 1) = x’y + x’y’ = x’ (y+y’) = x’ x 0 0 1 1 y 0 1 1 F 1 1 0 0 1 X’

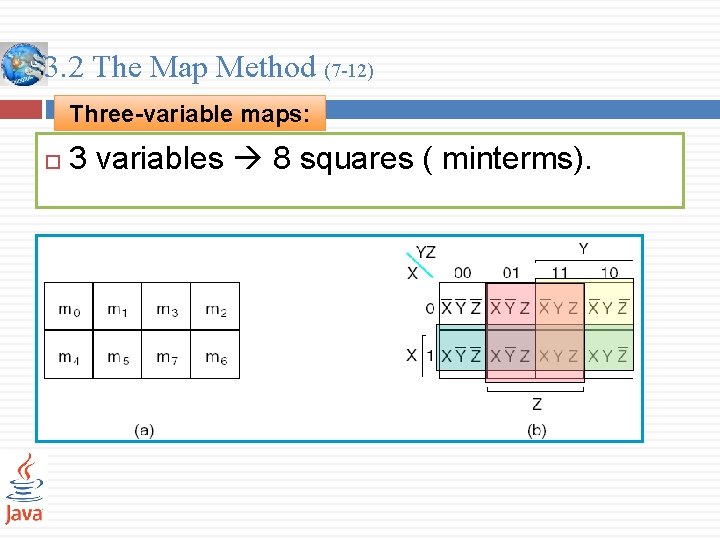
3. 2 The Map Method (7 -12) Three-variable maps: 3 variables 8 squares ( minterms).

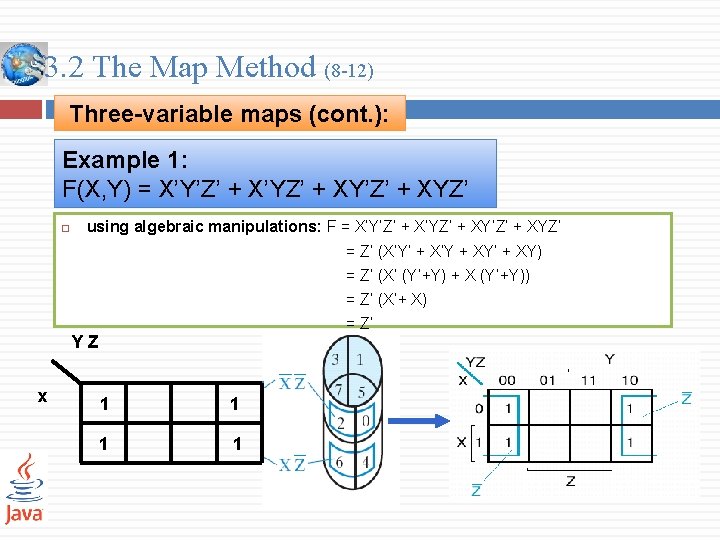
3. 2 The Map Method (8 -12) Three-variable maps (cont. ): Example 1: F(X, Y) = X’Y’Z’ + X’YZ’ + XY’Z’ + XYZ’ using algebraic manipulations: F = X’Y’Z’ + X’YZ’ + XY’Z’ + XYZ’ = Z’ (X’Y’ + X’Y + XY’ + XY) = Z’ (X’ (Y’+Y) + X (Y’+Y)) = Z’ (X’+ X) = Z’ YZ x 1 1

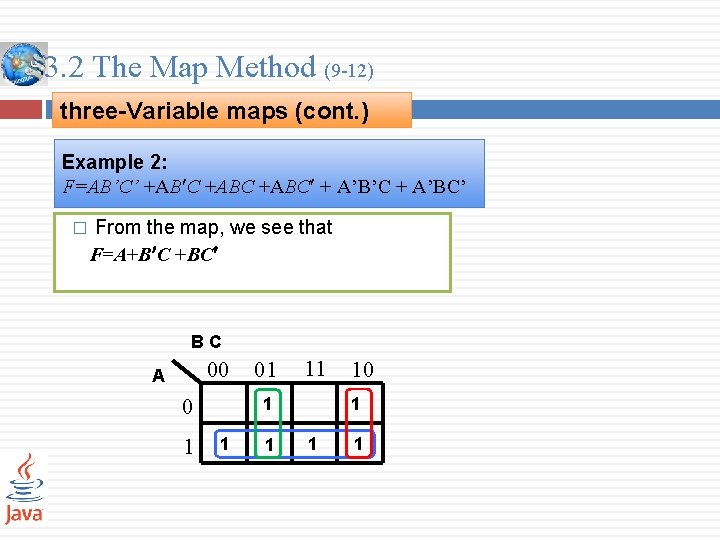
3. 2 The Map Method (9 -12) three-Variable maps (cont. ) Example 2: F=AB’C’ +AB C +ABC + A’B’C + A’BC’ � From the map, we see that F=A+B C +BC BC 00 A 0 1 01 11 1 10 1 1 1

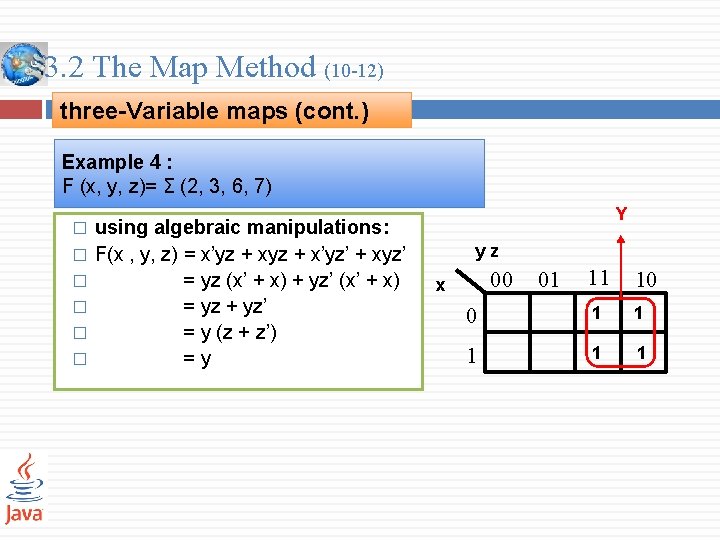
3. 2 The Map Method (10 -12) three-Variable maps (cont. ) Example 4 : F (x, y, z)= Σ (2, 3, 6, 7) � � � using algebraic manipulations: F(x , y, z) = x’yz + x’yz’ + xyz’ = yz (x’ + x) + yz’ (x’ + x) = yz + yz’ = y (z + z’) =y Y yz 11 10 0 1 1 1 00 x 01

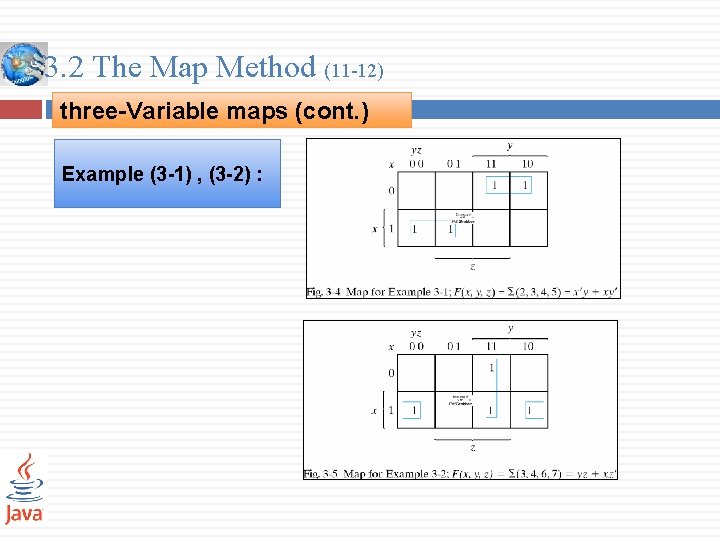
3. 2 The Map Method (11 -12) three-Variable maps (cont. ) Example (3 -1) , (3 -2) :

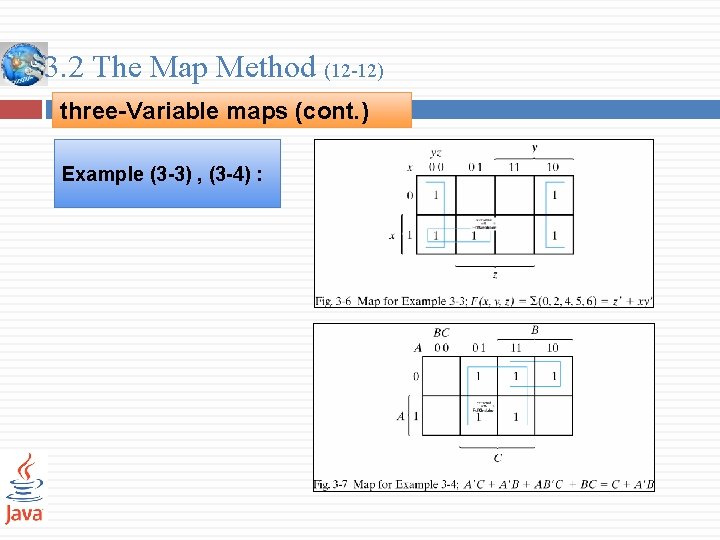
3. 2 The Map Method (12 -12) three-Variable maps (cont. ) Example (3 -3) , (3 -4) :

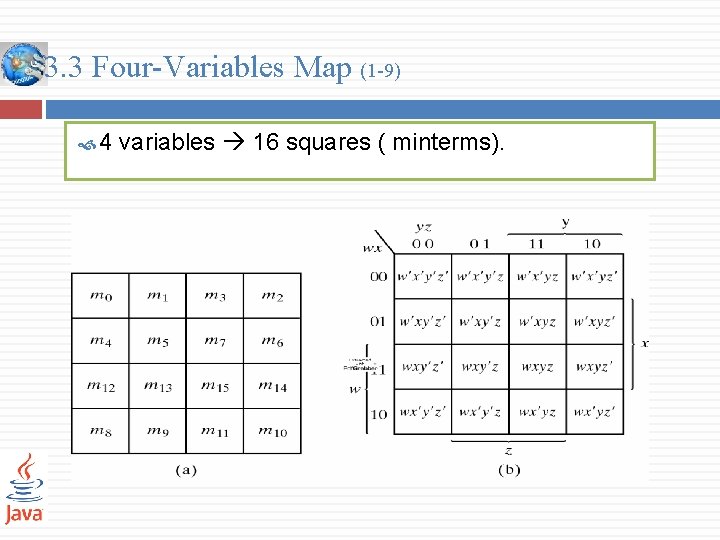
3. 3 Four-Variables Map (1 -9) 4 variables 16 squares ( minterms).

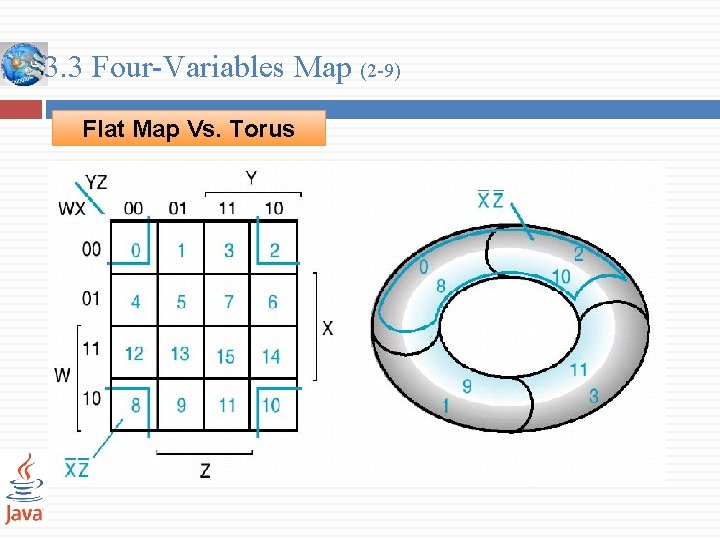
3. 3 Four-Variables Map (2 -9) Flat Map Vs. Torus

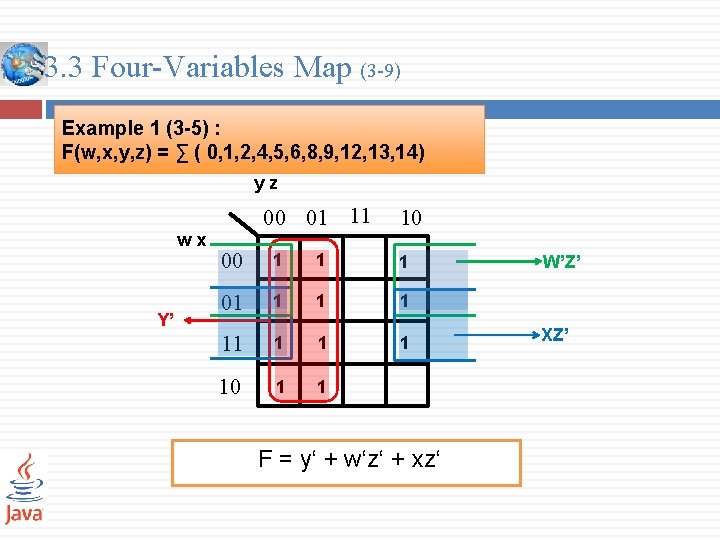
3. 3 Four-Variables Map (3 -9) Example 1 (3 -5) : F(w, x, y, z) = ∑ ( 0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) yz wx Y’ 00 01 11 10 00 1 1 1 01 1 1 1 10 1 1 F = y‘ + w‘z‘ + xz‘ W’Z’ XZ’

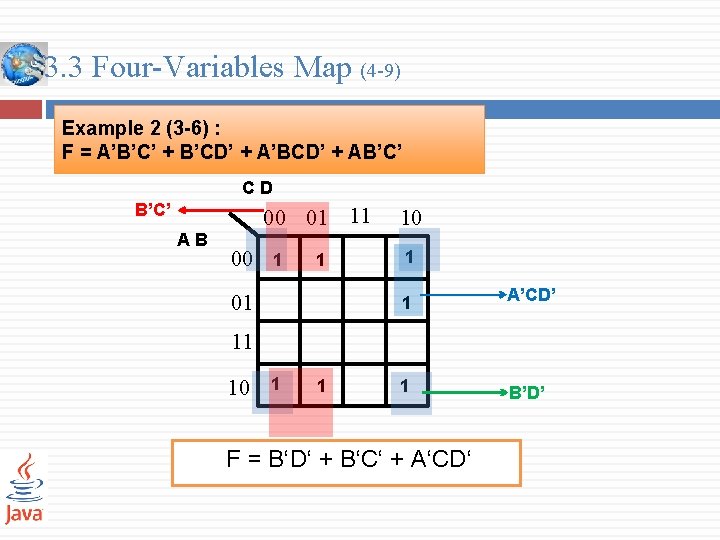
3. 3 Four-Variables Map (4 -9) Example 2 (3 -6) : F = A’B’C’ + B’CD’ + A’BCD’ + AB’C’ CD B’C’ AB 00 01 11 00 1 1 01 10 1 1 A’CD’ 1 B’D’ 11 10 1 1 F = B‘D‘ + B‘C‘ + A‘CD‘

3. 3 Four-Variables Map (5 -9) Simplification using Prime Implicants o A Prime Implicant is a product term obtained by combining the maximum possible number of adjacent squares in the map. o Essential : covered by only one prime implicant.

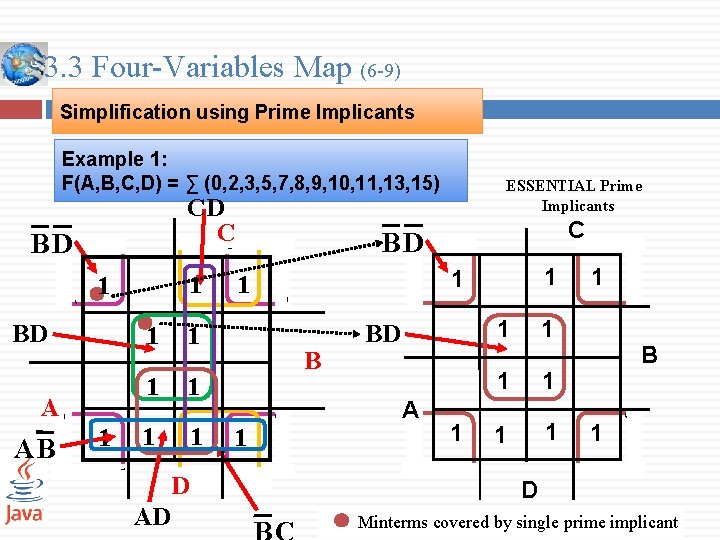
3. 3 Four-Variables Map (6 -9) Simplification using Prime Implicants Example 1: F(A, B, C, D) = ∑ (0, 2, 3, 5, 7, 8, 9, 10, 11, 13, 15) CD C BD 1 1 BD A AB 1 1 1 1 D AD ESSENTIAL Prime Implicants C BD B 1 1 1 BD 1 1 B A 1 1 1 D Minterms covered by single prime implicant

3. 3 Four-Variables Map (7 -9) Simplification using Prime Implicants Example 1: F(A, B, C, D) = ∑ (0, 2, 3, 5, 7, 8, 9, 10, 11, 13, 15) o Essential prime implicants: BD , B’D’ o Prime implicant: CD , B’C, AD , AB’. o The minterms that not cover by essential implicants are: m 3, m 9, m 11. v The simplified expression is optained from the sum of the essential implicants and other prime implicants that may be needed to cover any remaining minterms. o • • So this function can be written with these ways: F = BD + B’D’ + CD + AD F = BD + B’D’ + CD + AB’ F = BD + B’D’ + B’C + AD F = BD + B’D’ + B’C + AB’

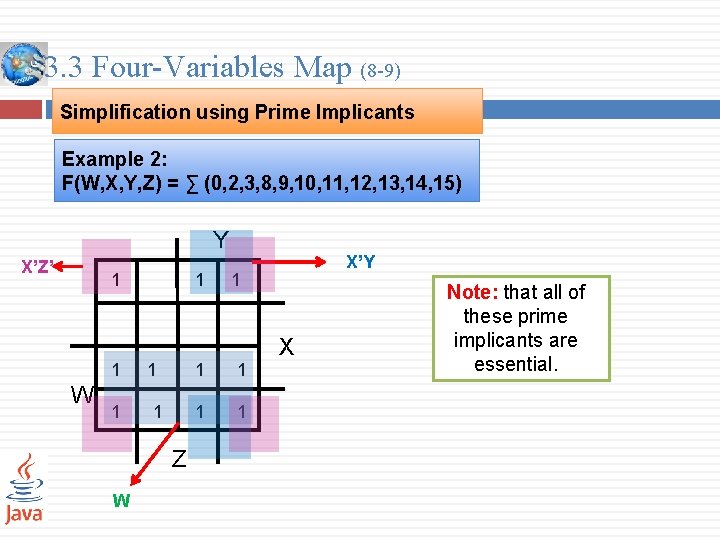
3. 3 Four-Variables Map (8 -9) Simplification using Prime Implicants Example 2: F(W, X, Y, Z) = ∑ (0, 2, 3, 8, 9, 10, 11, 12, 13, 14, 15) Y X’Z’ 1 1 W 1 1 Z W X’Y 1 1 1 X Note: that all of these prime implicants are essential.

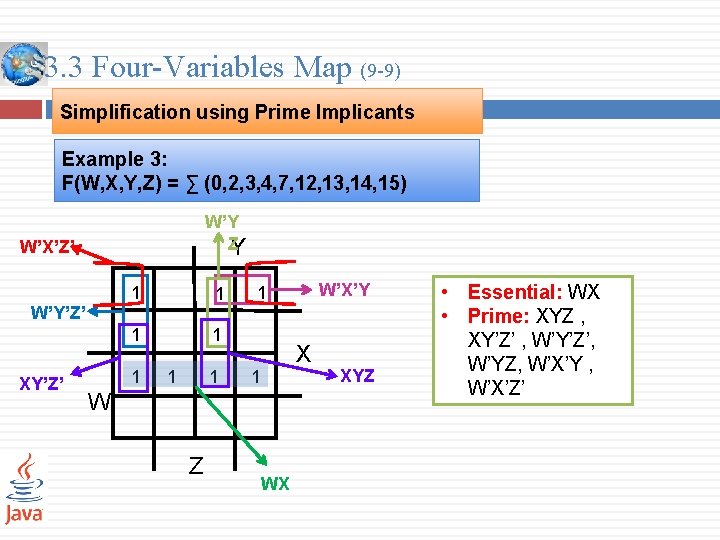
3. 3 Four-Variables Map (9 -9) Simplification using Prime Implicants Example 3: F(W, X, Y, Z) = ∑ (0, 2, 3, 4, 7, 12, 13, 14, 15) W’Y Z Y W’X’Z’ W’Y’Z’ XY’Z’ 1 1 1 1 X 1 W Z W’X’Y 1 WX XYZ • Essential: WX • Prime: XYZ , XY’Z’ , W’Y’Z’, W’YZ, W’X’Y , W’X’Z’

3. 5 Product-of-Sum simplification (1 -3) 1. Mark with 1’s the minterms of F. 2. Mark with 0’s the minterms of F’. 3. Circle 0’s to express F’. 4. Complement the result in step 3 to obtain a simplified F in product-of-sums form.

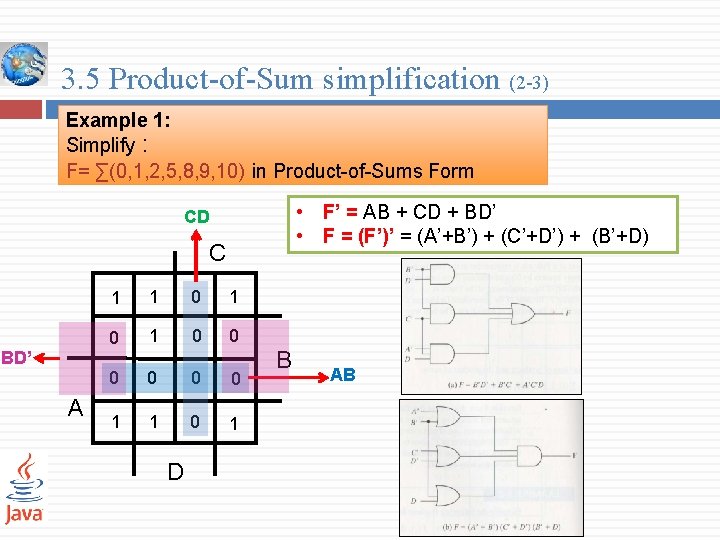
3. 5 Product-of-Sum simplification (2 -3) Example 1: Simplify : F= ∑(0, 1, 2, 5, 8, 9, 10) in Product-of-Sums Form • F’ = AB + CD + BD’ • F = (F’)’ = (A’+B’) + (C’+D’) + (B’+D) CD C BD’ A 1 1 0 1 0 0 0 1 1 0 1 D B AB

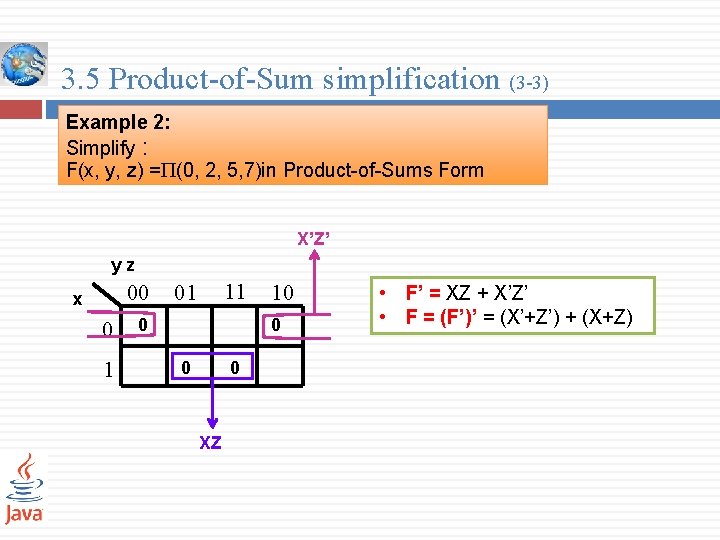
3. 5 Product-of-Sum simplification (3 -3) Example 2: Simplify : F(x, y, z) = (0, 2, 5, 7)in Product-of-Sums Form X’Z’ yz 00 x 0 1 11 01 0 10 0 XZ • F’ = XZ + X’Z’ • F = (F’)’ = (X’+Z’) + (X+Z)

3. 6 Don't Cares Condition (2 -4) Example : § A logic function having the binary codes for the BCD digits as its inputs. Only the codes for 0 through 9 are used. § The six codes, 1010 through 1111 never occur, so the output values for these codes are “x” to represent “don’t cares. ”

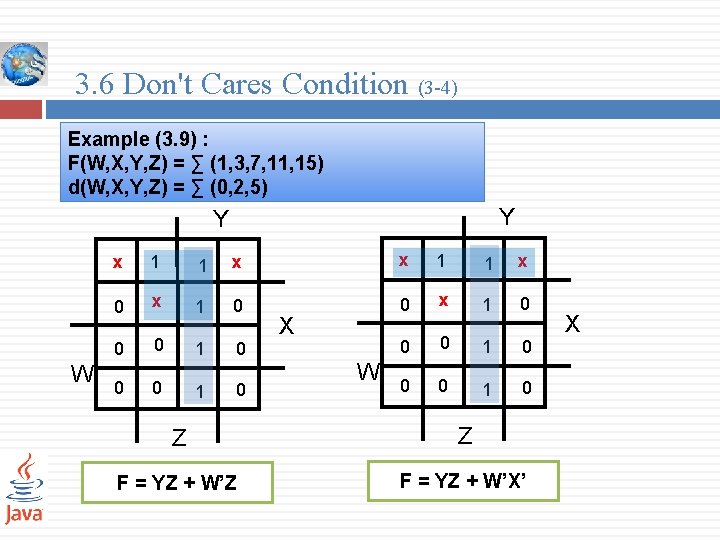
3. 6 Don't Cares Condition (3 -4) Example (3. 9) : F(W, X, Y, Z) = ∑ (1, 3, 7, 11, 15) d(W, X, Y, Z) = ∑ (0, 2, 5) Y Y W x 1 1 x 0 x 1 0 0 0 1 0 X W Z Z F = YZ + W’X’ X

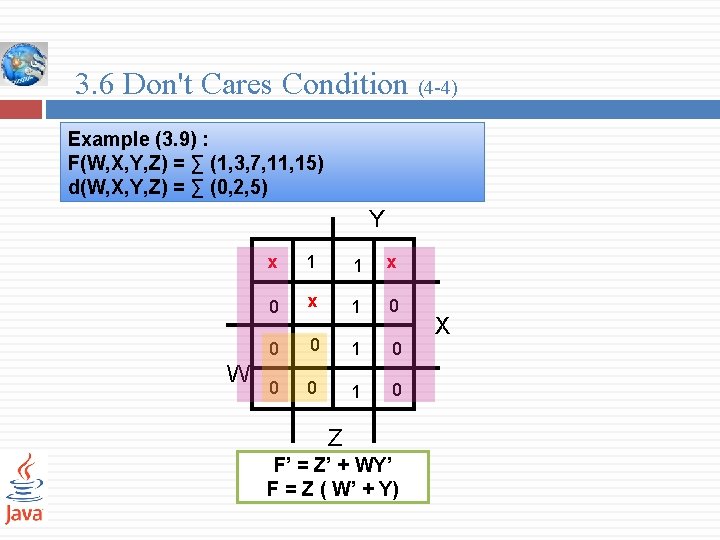
3. 6 Don't Cares Condition (4 -4) Example (3. 9) : F(W, X, Y, Z) = ∑ (1, 3, 7, 11, 15) d(W, X, Y, Z) = ∑ (0, 2, 5) Y W x 1 1 x 0 x 1 0 0 0 1 0 Z F’ = Z’ + WY’ F = Z ( W’ + Y) X

3. 7 NAND and NOR Implementation (1 -15) Digital circuits are frequently constructed with NAND or NOR gates rather than with AND and OR gates.

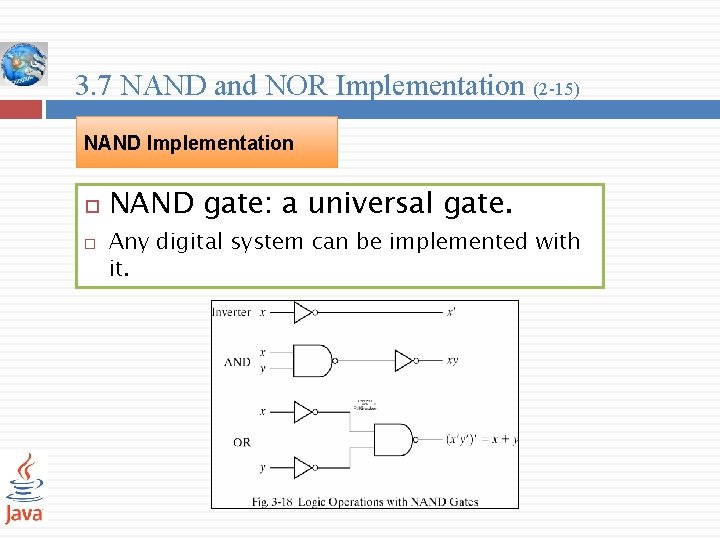
3. 7 NAND and NOR Implementation (2 -15) NAND Implementation NAND gate: a universal gate. Any digital system can be implemented with it.

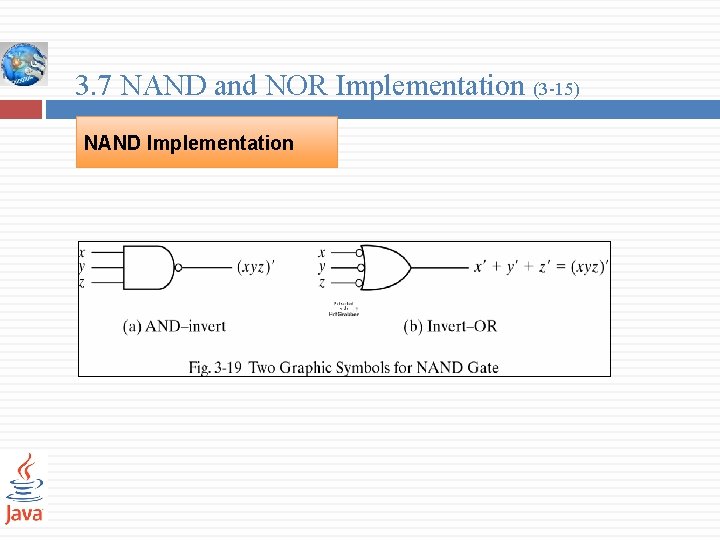
3. 7 NAND and NOR Implementation (3 -15) NAND Implementation

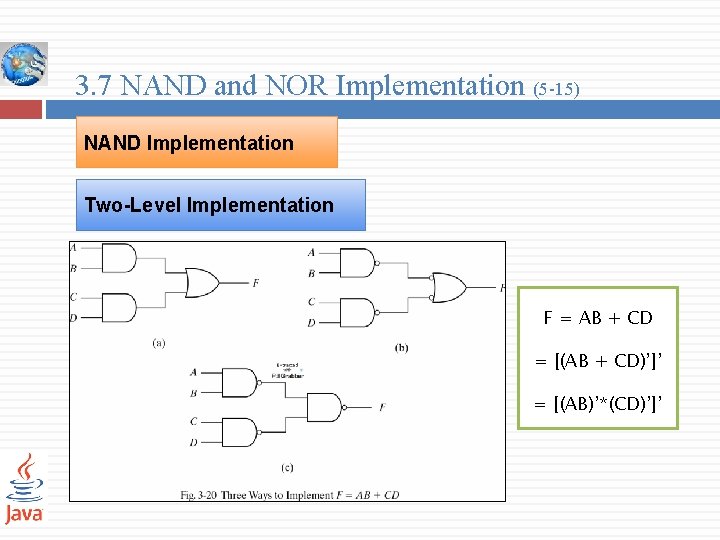
3. 7 NAND and NOR Implementation (5 -15) NAND Implementation Two-Level Implementation F = AB + CD = [(AB + CD)’]’ = [(AB)’*(CD)’]’

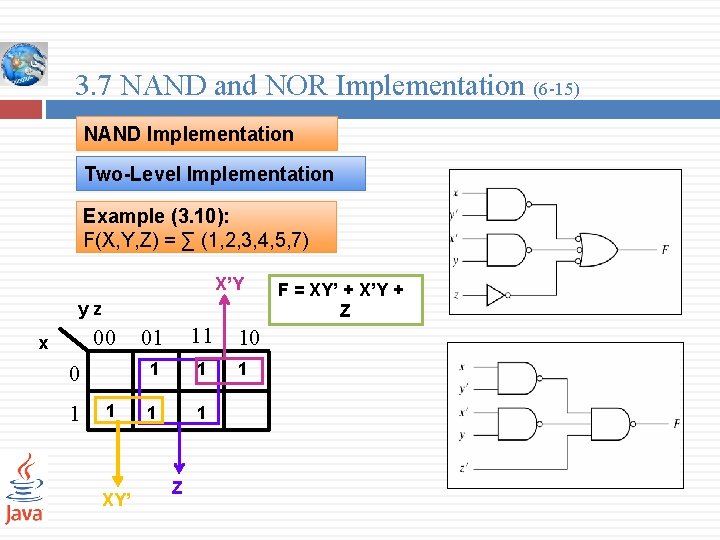
3. 7 NAND and NOR Implementation (6 -15) NAND Implementation Two-Level Implementation Example (3. 10): F(X, Y, Z) = ∑ (1, 2, 3, 4, 5, 7) X’Y yz 00 x 0 1 1 XY’ 01 11 1 1 Z 10 1 F = XY’ + X’Y + Z

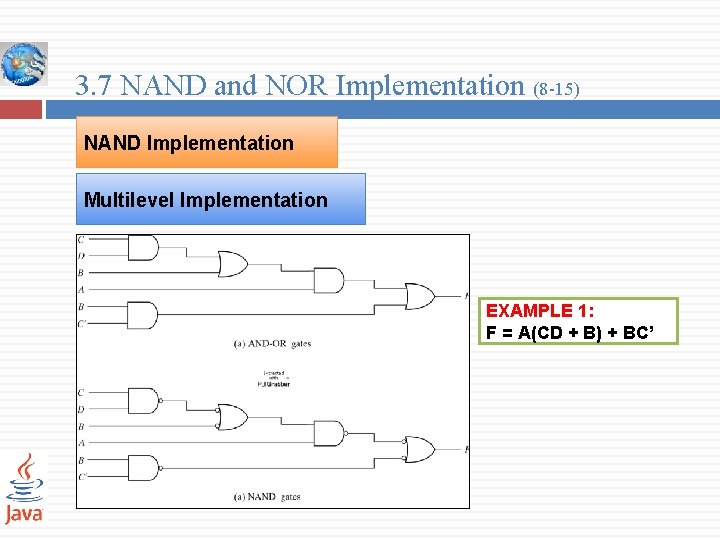
3. 7 NAND and NOR Implementation (8 -15) NAND Implementation Multilevel Implementation EXAMPLE 1: F = A(CD + B) + BC’

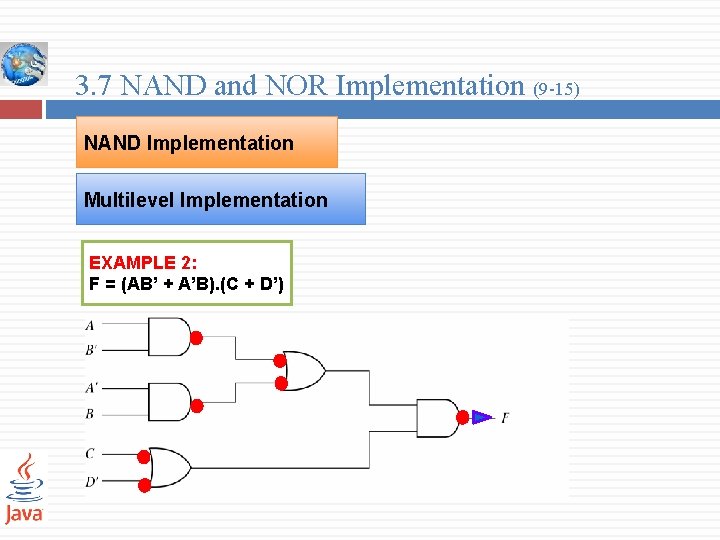
3. 7 NAND and NOR Implementation (9 -15) NAND Implementation Multilevel Implementation EXAMPLE 2: F = (AB’ + A’B). (C + D’)

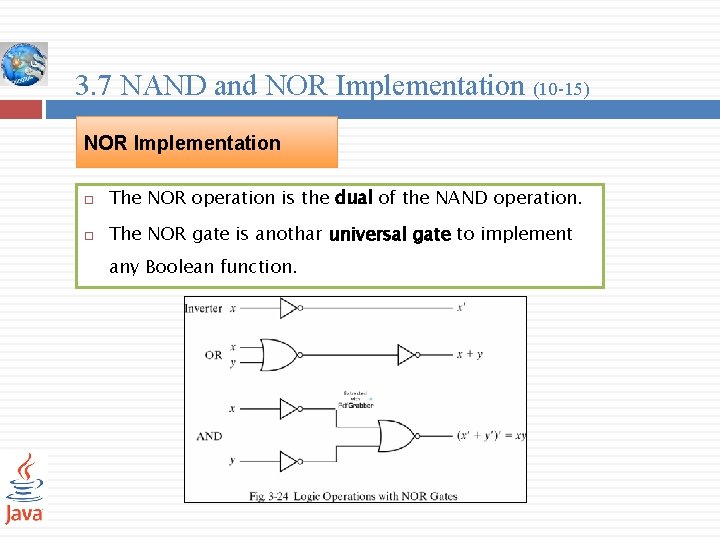
3. 7 NAND and NOR Implementation (10 -15) NOR Implementation The NOR operation is the dual of the NAND operation. The NOR gate is anothar universal gate to implement any Boolean function.

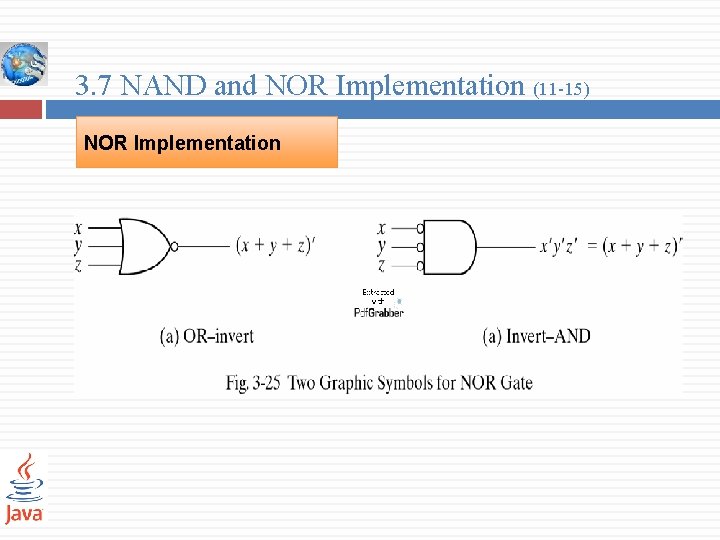
3. 7 NAND and NOR Implementation (11 -15) NOR Implementation

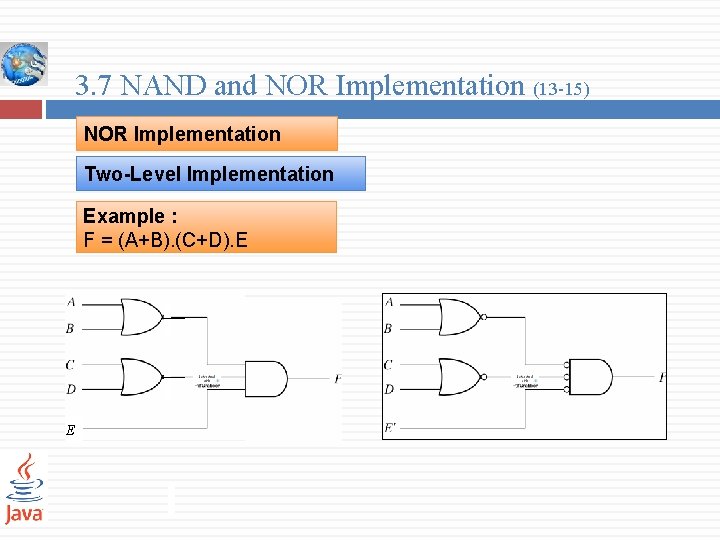
3. 7 NAND and NOR Implementation (13 -15) NOR Implementation Two-Level Implementation Example : F = (A+B). (C+D). E E

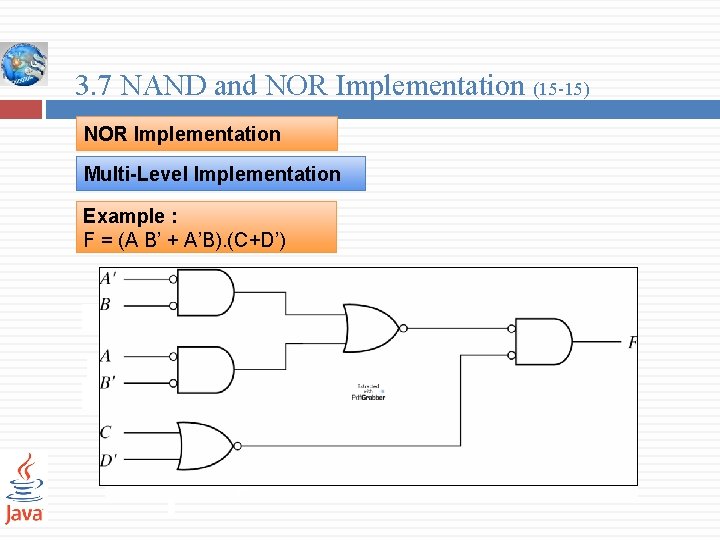
3. 7 NAND and NOR Implementation (15 -15) NOR Implementation Multi-Level Implementation Example : F = (A B’ + A’B). (C+D’) A B’ A’ B

3. 8 Other Two-Level Implementations (1 -7) Nondegeneratd forms Implementation 16 possible combinations of two-level forms with 4 types of gates: AND, OR, NAND, and NOR 8 are degenerate forms: degenerate to a single operation. v (AND-AND , AND-NAND, OR-OR , OR-NOR , NAND-NAND , NAND-NOR , NOR-AND , NOR-NAND) 8 are generate forms: v NAND-AND = AND-NOR = AND-OR-INVERT v OR-NAND = NOR-OR = OR-AND-INVERT

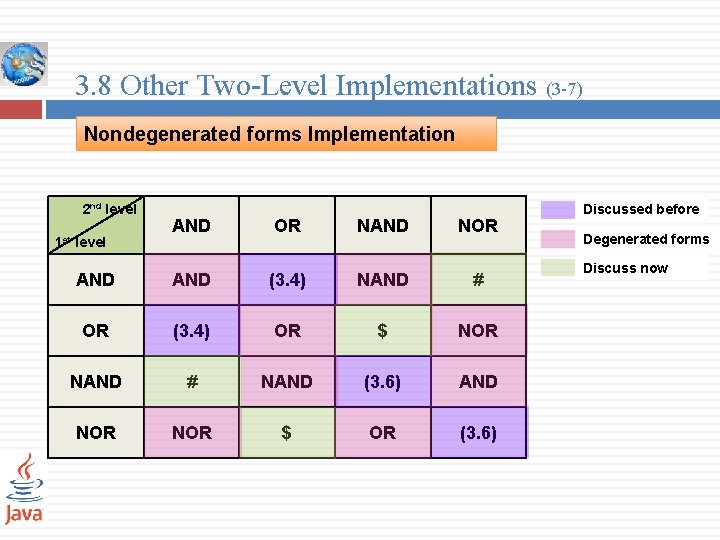
3. 8 Other Two-Level Implementations (3 -7) Nondegenerated forms Implementation 2 nd level AND OR NAND NOR AND (3. 4) NAND # OR (3. 4) OR $ NOR NAND # NAND (3. 6) AND NOR $ OR (3. 6) 1 st level Discussed before Degenerated forms Discuss now

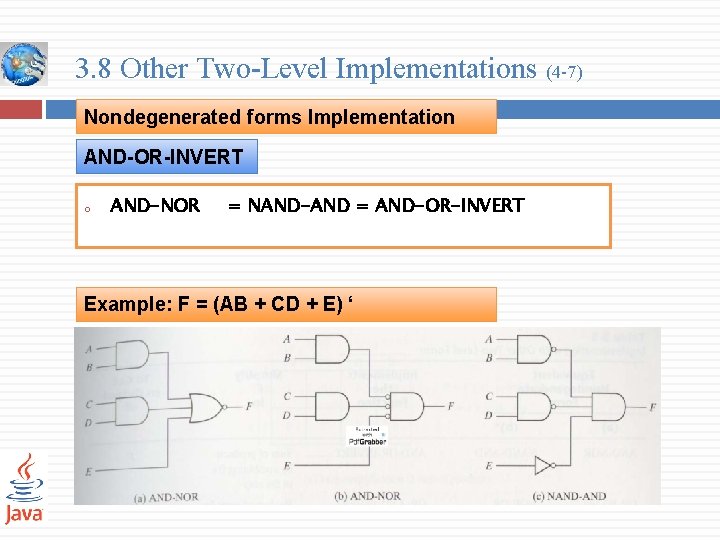
3. 8 Other Two-Level Implementations (4 -7) Nondegenerated forms Implementation AND-OR-INVERT o AND-NOR = NAND-AND = AND-OR-INVERT Example: F = (AB + CD + E) ‘

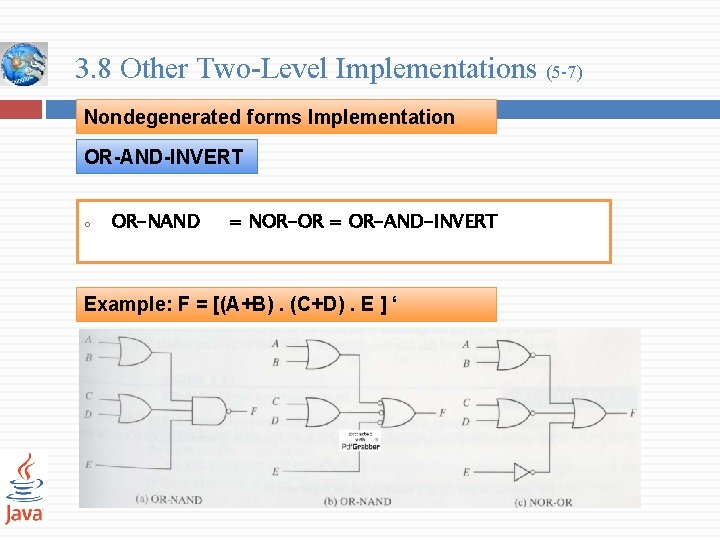
3. 8 Other Two-Level Implementations (5 -7) Nondegenerated forms Implementation OR-AND-INVERT o OR-NAND = NOR-OR = OR-AND-INVERT Example: F = [(A+B). (C+D). E ] ‘

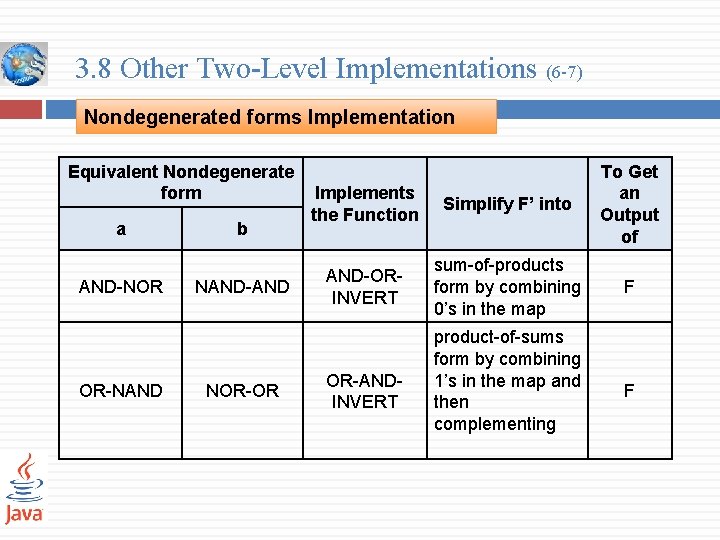
3. 8 Other Two-Level Implementations (6 -7) Nondegenerated forms Implementation Equivalent Nondegenerate form a AND-NOR OR-NAND b NAND-AND NOR-OR Implements the Function Simplify F’ into To Get an Output of AND-ORINVERT sum-of-products form by combining 0’s in the map F OR-ANDINVERT product-of-sums form by combining 1’s in the map and then complementing F

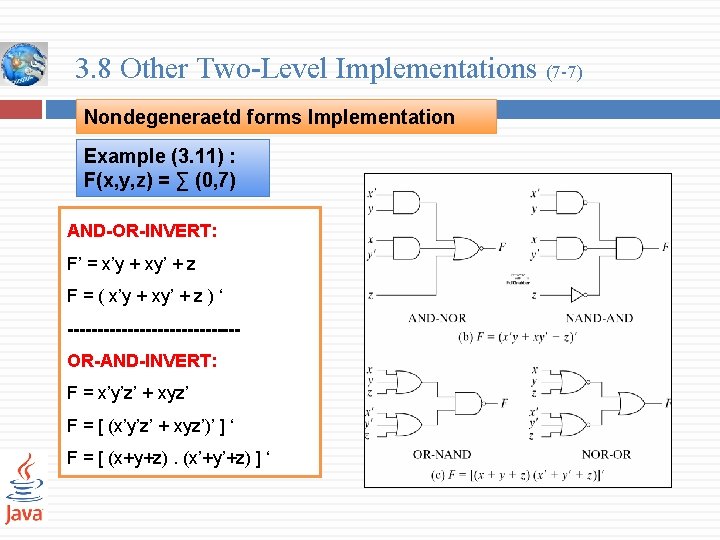
3. 8 Other Two-Level Implementations (7 -7) Nondegeneraetd forms Implementation Example (3. 11) : F(x, y, z) = ∑ (0, 7) AND-OR-INVERT: F’ = x’y + xy’ + z F = ( x’y + xy’ + z ) ‘ --------------OR-AND-INVERT: F = x’y’z’ + xyz’ F = [ (x’y’z’ + xyz’)’ ] ‘ F = [ (x+y+z). (x’+y’+z) ] ‘

3. 9 Exclusive-OR Function (1 -9) Exclusive-OR (XOR) denoted by the symbol : v x y = xy‘ + x‘y Exclusive-NOR (XNOR): v (x y )‘ = xy + x‘y‘

3. 9 Exclusive-OR Function (2 -9) Exclusive-OR principles: x 0=x x 1 = x‘ x x=0 x x‘ = 1 x y‘ = x‘ y = (x y)‘ x y=y x (x y) z = x (y z)

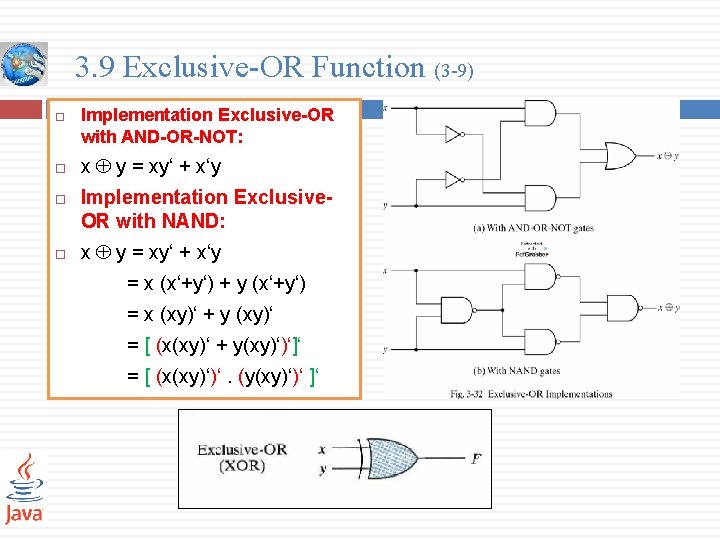
3. 9 Exclusive-OR Function (3 -9) Implementation Exclusive-OR with AND-OR-NOT: x y = xy‘ + x‘y Implementation Exclusive. OR with NAND: x y = xy‘ + x‘y = x (x‘+y‘) + y (x‘+y‘) = x (xy)‘ + y (xy)‘ = [ (x(xy)‘ + y(xy)‘)‘]‘ = [ (x(xy)‘)‘. (y(xy)‘)‘ ]‘

3. 9 Exclusive-OR Function (4 -9) Odd Function: Multiple-variable exclusive OR operation = odd function (A B C) = (AB‘ + A‘B) C‘ + (A‘B‘ + AB) C = AB‘C‘ + A‘B‘C + ABC = ∑ (1, 2, 4, 7)

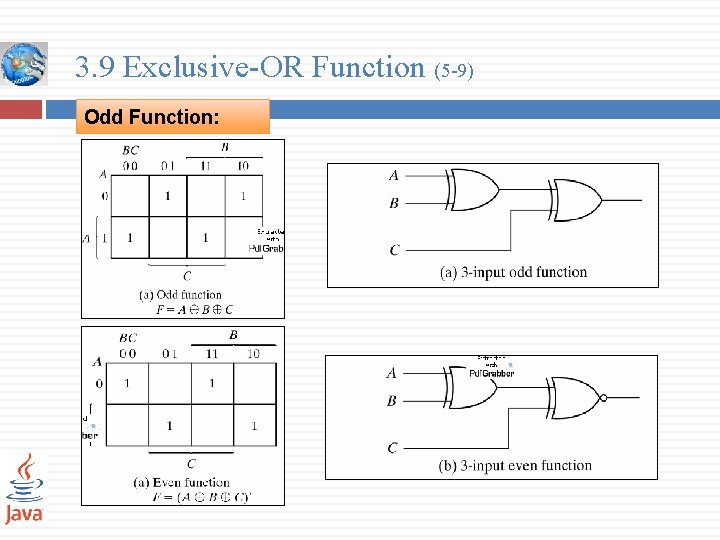
3. 9 Exclusive-OR Function (5 -9) Odd Function:

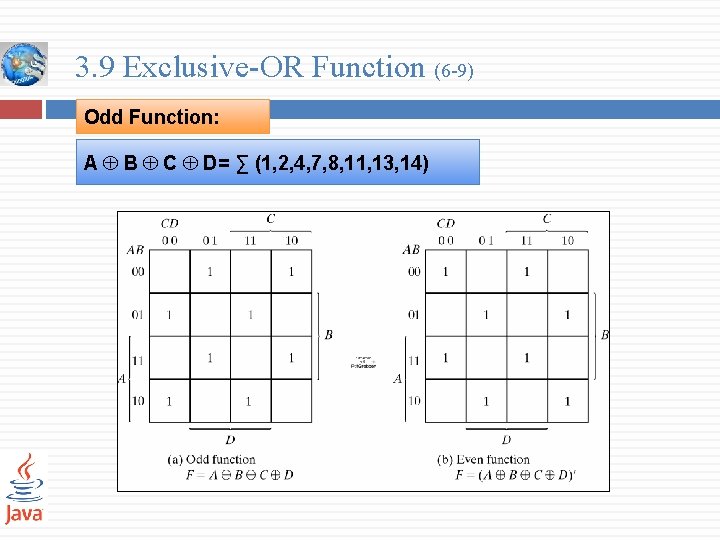
3. 9 Exclusive-OR Function (6 -9) Odd Function: A B C D= ∑ (1, 2, 4, 7, 8, 11, 13, 14)

3. 9 Exclusive-OR Function (7 -9) Parity Generation and Checking: Parity bit : an extra bit included with a binary message to make the number of 1’s either odd or even. � � parity generator. parity checker.

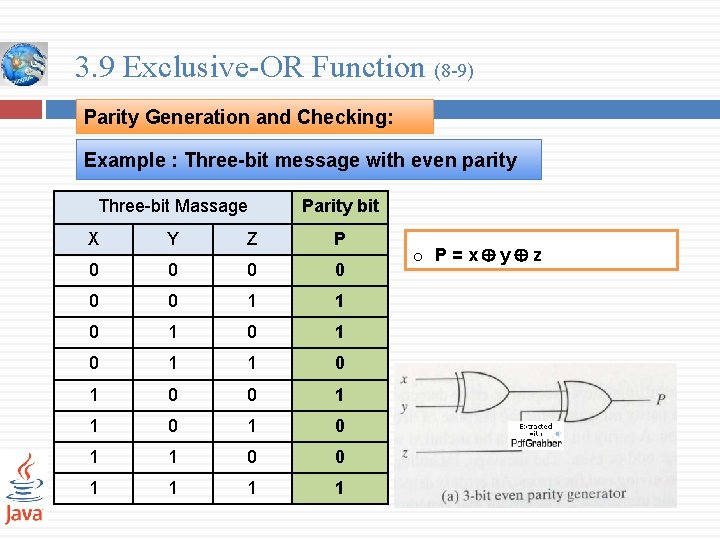
3. 9 Exclusive-OR Function (8 -9) Parity Generation and Checking: Example : Three-bit message with even parity Three-bit Massage Parity bit X Y Z P 0 0 0 1 1 0 1 0 1 0 0 1 1 0 0 1 1 o P=x y z

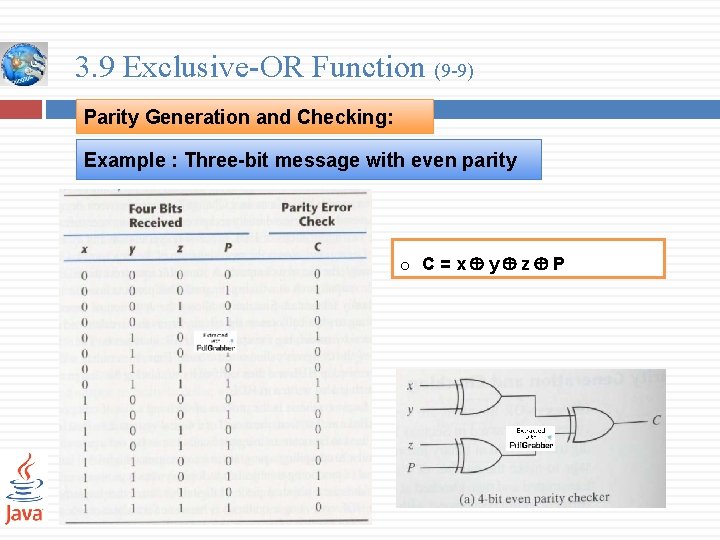
3. 9 Exclusive-OR Function (9 -9) Parity Generation and Checking: Example : Three-bit message with even parity o C=x y z P