Chapter 18 Superposition and Standing Waves 1 Waves
















































- Slides: 62

Chapter 18 Superposition and Standing Waves 1

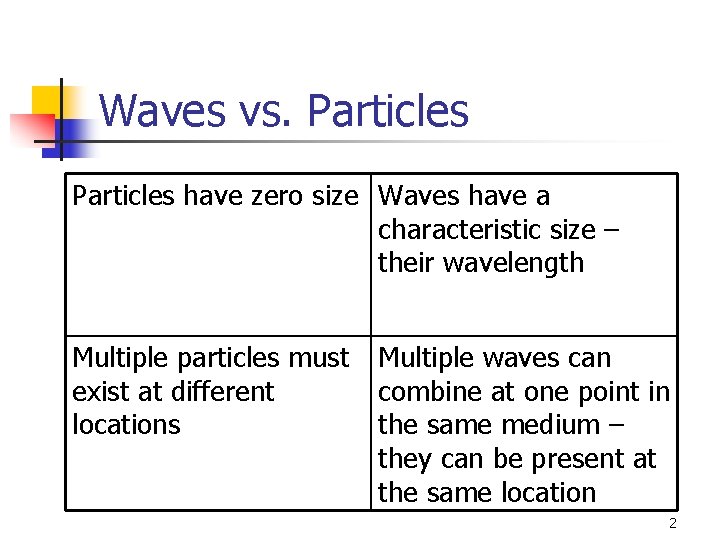
Waves vs. Particles have zero size Waves have a characteristic size – their wavelength Multiple particles must exist at different locations Multiple waves can combine at one point in the same medium – they can be present at the same location 2

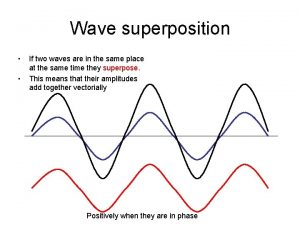
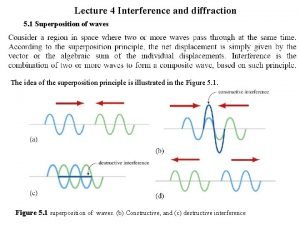
Superposition Principle n n If two or more traveling waves are moving through a medium, the resultant value of the wave function at any point is the algebraic sum of the values of the wave functions of the individual waves Waves that obey the superposition principle are linear waves 3

Superposition and Interference n Two traveling waves can pass through each other without being destroyed or altered n n A consequence of the superposition principle The combination of separate waves in the same region of space to produce a resultant wave is called interference 4

Superposition Example n n Two pulses are traveling in opposite directions (a). The pulses have the same speed but different shapes. The displacement of the elements is positive for both. When the waves start to overlap (b), the resultant wave function is y 1 + y 2. 5

n n n Superposition Example, cont When crest meets crest (c) the resultant wave has a larger amplitude than either of the original waves. The two pulses separate (d). They continue moving in their original directions. n The shapes of the pulses remain unchanged. n This type of superposition is called constructive interference. 6

Destructive Interference Example n n Two pulses traveling in opposite directions. Their displacements are inverted with respect to each other. When these pulses overlap, the resultant pulse is y 1 + y 2. This type of superposition is called destructive interference. 7

Types of Interference n Constructive interference occurs when the displacements caused by the two pulses are in the same direction n n The amplitude of the resultant pulse is greater than either individual pulse Destructive interference occurs when the displacements caused by the two pulses are in opposite directions n The amplitude of the resultant pulse is less than either individual pulse 8

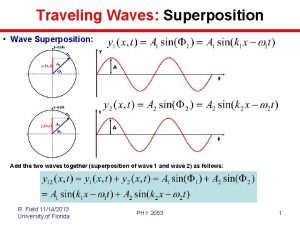
Superposition of Sinusoidal Waves n n n Assume two waves are traveling in the same direction, with the same frequency, wavelength and amplitude The waves differ in phase y 1 = A sin (kx - wt) y 2 = A sin (kx - wt + f) y = y 1 + y 2 = 2 A cos (f/2) sin (kx - wt + f/2) 9

Superposition of Sinusoidal Waves, cont n n The resultant wave function, y, is also sinusoidal The resultant wave has the same frequency and wavelength as the original waves The amplitude of the resultant wave is 2 A cos (f/2) The phase of the resultant wave is f/2 10

Sinusoidal Waves with Constructive Interference n n When f = 0, then cos (f/2) = 1 The amplitude of the resultant wave is 2 A n n n The crests of one wave coincide with the crests of the other wave The waves are everywhere in phase The waves interfere constructively 11

Sinusoidal Waves with Destructive Interference n When f = p, then cos (f/2) = 0 n n The amplitude of the resultant wave is 0 n n Also any odd multiple of p Crests of one wave coincide with troughs of the other wave The waves interfere destructively 12

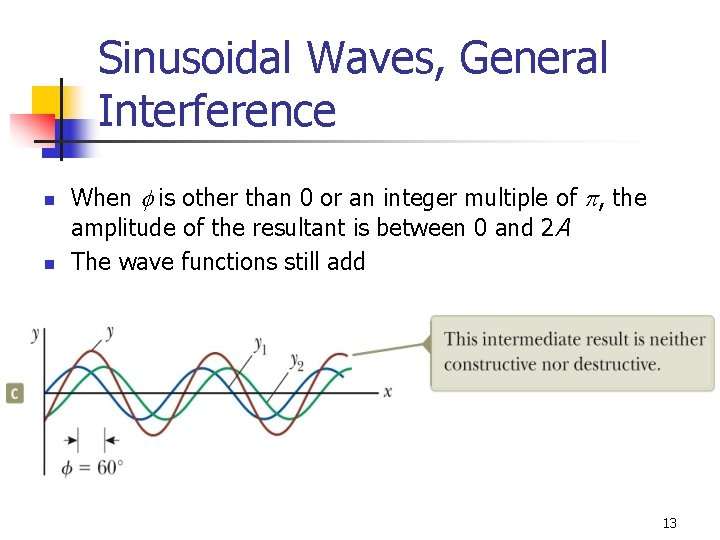
Sinusoidal Waves, General Interference n n When f is other than 0 or an integer multiple of p, the amplitude of the resultant is between 0 and 2 A The wave functions still add 13

Sinusoidal Waves, Summary of Interference n Constructive interference occurs when f = 0 n n Destructive interference occurs when f = np where n is an odd integer n n Amplitude of the resultant is 2 A Amplitude is 0 General interference occurs when 0 < f < np n Amplitude is 0 < Aresultant < 2 A 14

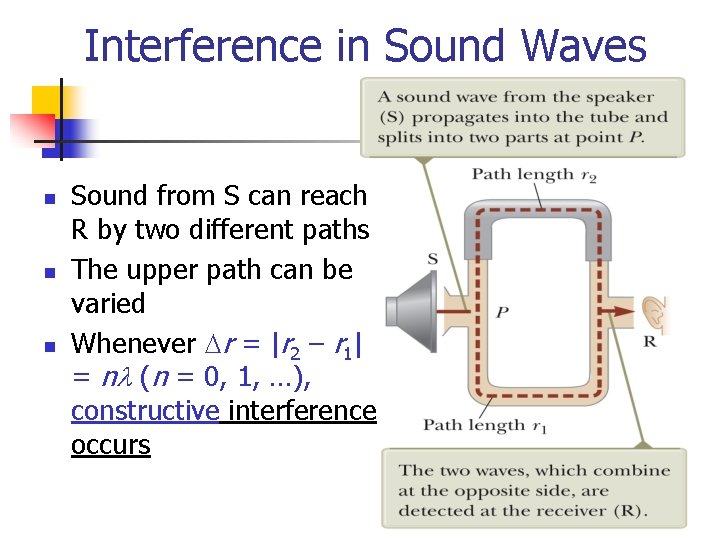
Interference in Sound Waves n n n Sound from S can reach R by two different paths The upper path can be varied Whenever Dr = |r 2 – r 1| = nl (n = 0, 1, …), constructive interference occurs 15

Interference in Sound Waves, 2 n n n Whenever Dr = |r 2 – r 1| = n(l/2) (n is odd), destructive interference occurs A phase difference may arise between two waves generated by the same source when they travel along paths of unequal lengths In general, the path difference can be expressed in terms of the phase angle 16

Interference in Sound Waves, final Using the relationship between Dr and f allows an expression for the conditions of interference n If the path difference is any even multiple of λ/2( ), then f = 2 np where n = 0, 1, 2, … and the interference is constructive n If the path difference is any odd multiple of λ/2( ), then f = (2 n+1)p where n = 0, 1, 2, … and the interference is destructive n 17

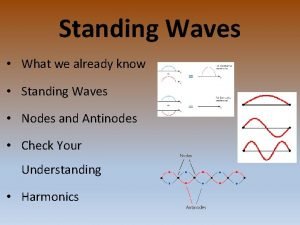
Standing Waves n n n Assume two waves with the same amplitude, frequency and wavelength, traveling in opposite directions in a medium y 1 = A sin(kx – wt) and y 2 = A sin(kx + wt) They interfere according to the superposition principle 18

Standing Waves, cont n n The resultant wave will be y = (2 Asinkx)coswt This is the wave function of a standing wave n n There is no kx – wt term, and therefore it is not a traveling wave In observing a standing wave, there is no sense of motion in the direction of propagation of either of the original waves 19

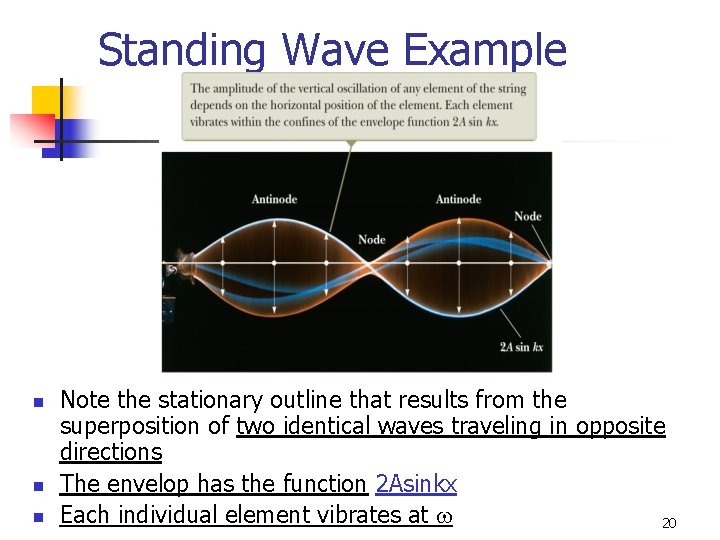
Standing Wave Example n n n Note the stationary outline that results from the superposition of two identical waves traveling in opposite directions The envelop has the function 2 Asinkx Each individual element vibrates at w 20

Note on Amplitudes n There are three types of amplitudes used in describing waves n n n The amplitude of the individual waves, A The amplitude of the simple harmonic motion of the elements in the medium, 2 Asinkx The amplitude of the standing wave, 2 A n A given element in a standing wave vibrates within the constraints of the envelope function 2 Asinkx, where x is the position of the element in the medium 21

Standing Waves, Particle Motion n n Every element in the medium oscillates in simple harmonic motion with the same frequency, w However, the amplitude of the simple harmonic motion depends on the location of the element within the medium 22

Standing Waves, Definitions n A node occurs at a point of zero amplitude n n These correspond to positions of x where An antinode occurs at a point of maximum displacement, 2 A n These correspond to positions of x where 23

Features of Nodes and Antinodes n The distance between adjacent antinodes is l/2 n The distance between adjacent nodes is l/2 n The distance between a node and an adjacent antinode is l/4 24

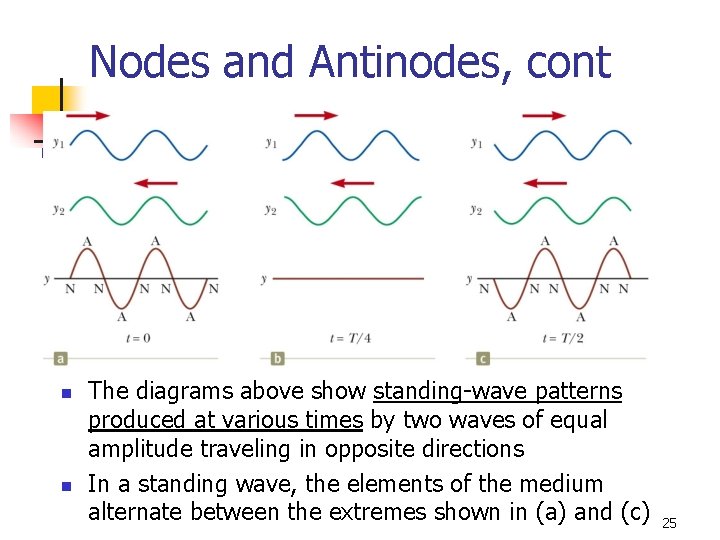
Nodes and Antinodes, cont n n The diagrams above show standing-wave patterns produced at various times by two waves of equal amplitude traveling in opposite directions In a standing wave, the elements of the medium alternate between the extremes shown in (a) and (c) 25

Standing Waves in a String n n Consider a string fixed at both ends The string has length L Standing waves are set up by a continuous superposition of waves incident on and reflected from the ends There is a boundary condition on the waves 26

Standing Waves in a String, 2 n The ends of the strings must necessarily be nodes n n They are fixed and therefore must have zero displacement The boundary condition results in the string having a set of normal modes of vibration n n Each mode has a characteristic frequency The normal modes of oscillation for the string can be described by imposing the requirements that the ends be nodes and that the nodes and antinodes are separated by l/4 27

Standing Waves in a String, 3 n n This is the first normal mode that is consistent with the boundary conditions There are nodes at both ends There is one antinode in the middle This is the longest wavelength mode n (½)l = L so l = 2 L 28

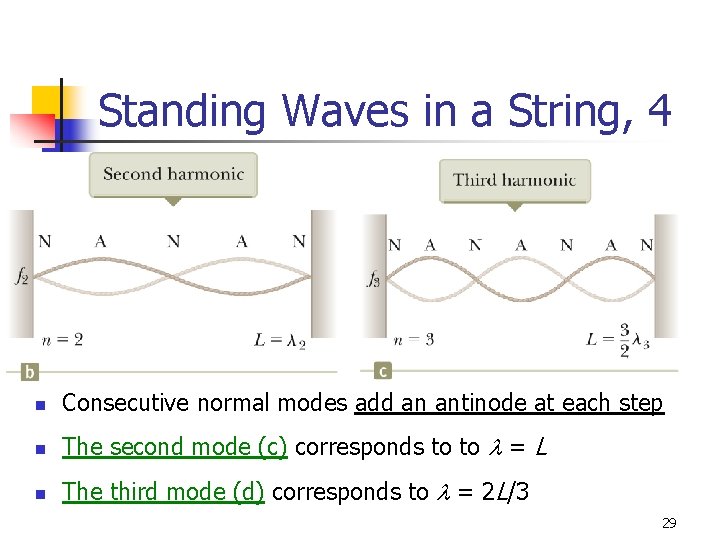
Standing Waves in a String, 4 n Consecutive normal modes add an antinode at each step n The second mode (c) corresponds to to l = L n The third mode (d) corresponds to l = 2 L/3 29

Standing Waves on a String, Summary n n The wavelengths of the normal modes for a string of length L fixed at both ends are ln = 2 L / n n = 1, 2, 3, … n n is the nth normal mode of oscillation n These are the possible modes for the string The natural frequencies are 30

Quantization n n This situation in which only certain frequencies of oscillation are allowed is called quantization Quantization is a common occurrence when waves are subject to boundary conditions 31

Waves on a String, Harmonic Series n The fundamental frequency corresponds to n=1 n n It is the lowest frequency, ƒ 1 The frequencies of the remaining natural modes are integer multiples of the fundamental frequency n ƒn = nƒ 1 Frequencies of normal modes that exhibit this relationship form a harmonic series The normal modes are called harmonics 32

Musical Note of a String n n The musical note is defined by its fundamental frequency The frequency of the string can be changed by changing either its length or its tension 33

Harmonics, Example n A middle “C” on a piano has a fundamental frequency of 262 Hz. What are the next two harmonics of this string? n n n ƒ 1 = 262 Hz ƒ 2 = 2ƒ 1 = 524 Hz ƒ 3 = 3ƒ 1 = 786 Hz 34

Standing Wave on a String, Example Set-Up n n One end of the string is attached to a vibrating blade The other end passes over a pulley with a hanging mass attached to the end n n This produces the tension in the string The string is vibrating in its second harmonic 35

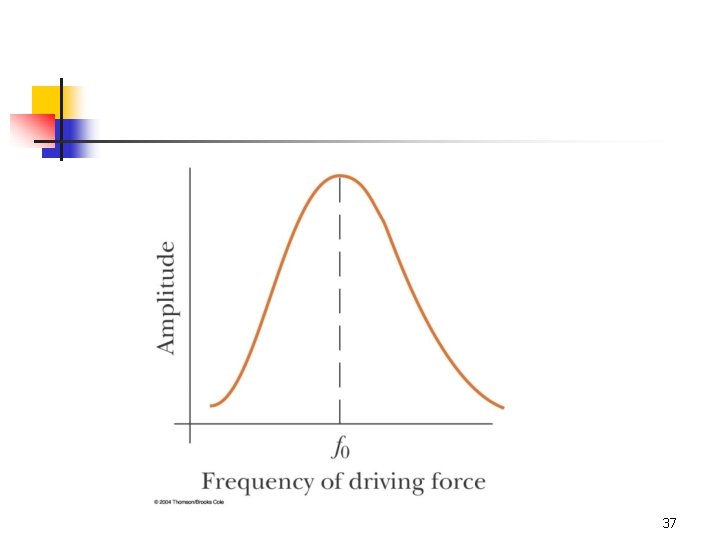
Resonance n n A system is capable of oscillating in one or more normal modes If a periodic force is applied to such a system, the amplitude of the resulting motion is greatest when the frequency of the applied force is equal to one of the natural frequencies of the system 36

37

Resonance, cont n n This phenomena is called resonance Because an oscillating system exhibits a large amplitude when driven at any of its natural frequencies, these frequencies are referred to as resonance frequencies The resonance frequency is symbolized by ƒo If the system is driven at a frequency that is not one of the natural frequencies, the oscillations are of low amplitude and exhibit no stable pattern 38

Resonance Example n n Standing waves are set up in a string when one end is connected to a vibrating blade When the blade vibrates at one of the natural frequencies of the string, large-amplitude standing waves are produced 39

Standing Waves in Air Columns n n n Standing waves can be set up in air columns as the result of interference between longitudinal sound waves traveling in opposite directions The phase relationship between the incident and reflected waves depends upon whether the end of the pipe is opened or closed Waves under boundary conditions model can be applied 40

Standing Waves in Air Columns, Closed End n A closed end of a pipe is a displacement node in the standing wave n n n The wall at this end will not allow longitudinal motion in the air The reflected wave is 180 o out of phase with the incident wave The closed end corresponds with a pressure antinode n It is a point of maximum pressure variations 41

Standing Waves in Air Columns, Open End n The open end of a pipe is a displacement antinode in the standing wave n n As the compression region of the wave exits the open end of the pipe, the constraint of the pipe is removed and the compressed air is free to expand into the atmosphere The open end corresponds with a pressure node n It is a point of no pressure variation 42

Standing Waves in an Open Tube n n n Both ends are displacement antinodes The fundamental frequency is v/2 L n This corresponds to the first diagram The higher harmonics are ƒn = nƒ 1 = n (v/2 L) where n = 1, 2, 3, … 43

Standing Waves in a Tube Closed at One End n n The closed end is a displacement node The open end is a displacement antinode The fundamental frequency is v/4 L The frequencies are ƒn = nƒ = n (v/4 L) where n = 1, 3, 5, … 44

Standing Waves in Air Columns, Summary n n In a pipe open at both ends, the natural frequencies of oscillation form a harmonic series that includes all integral multiples of the fundamental frequency In a pipe closed at one end, the natural frequencies of oscillations form a harmonic series that includes only odd integral multiples of the fundamental frequency 45

Notes About Instruments n As the temperature rises: n Sounds produced by air columns become sharp n Higher frequency n Higher speed due to the higher temperature n Sounds produced by strings become flat n Lower frequency n The strings expand due to the higher temperature n As the strings expand, their tension decreases 46

More About Instruments n n n Musical instruments based on air columns are generally excited by resonance The air column is presented with a sound wave that is rich in many frequencies The sound is provided by: n n n A vibrating reed in woodwinds Vibrations of the player’s lips in brasses Blowing over the edge at the mouthpiece of a flute 47

Resonance in Air Columns, Example n n A tuning fork is placed near the top of the tube When L corresponds to a resonance frequency of the pipe, the sound is louder The water acts as a closed end of a tube The wavelengths can be calculated from the lengths where resonance occurs 48

Standing Waves in Rods n n n A rod is clamped in the middle It is stroked parallel to the rod The rod will oscillate The clamp forces a displacement node The ends of the rod are free to vibrate and so will correspond to displacement antinodes 49

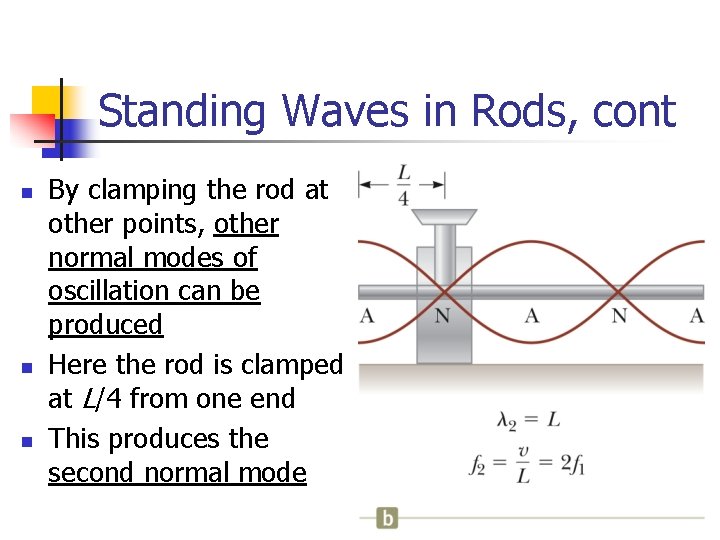
Standing Waves in Rods, cont n n n By clamping the rod at other points, other normal modes of oscillation can be produced Here the rod is clamped at L/4 from one end This produces the second normal mode 50

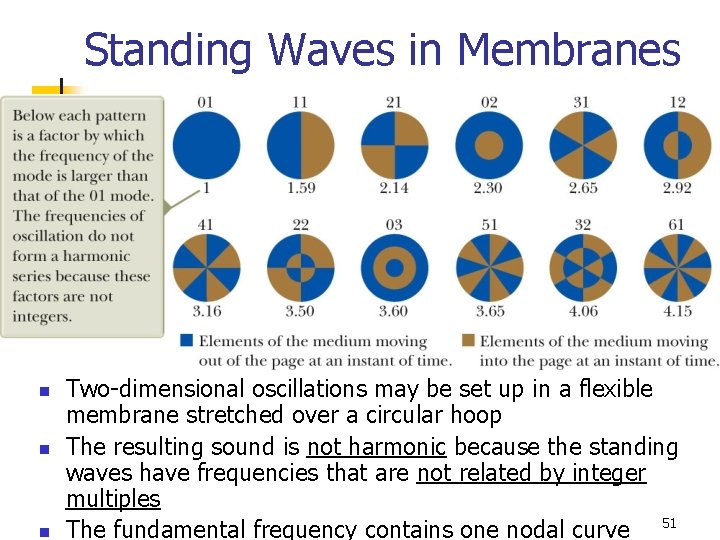
Standing Waves in Membranes n n n Two-dimensional oscillations may be set up in a flexible membrane stretched over a circular hoop The resulting sound is not harmonic because the standing waves have frequencies that are not related by integer multiples The fundamental frequency contains one nodal curve 51

Spatial and Temporal Interference n Spatial interference occurs when the amplitude of the oscillation in a medium varies with the position in space of the element n n This is the type of interference discussed so far Temporal interference occurs when waves are periodically in and out of phase n There is a temporal alternation between constructive and destructive interference 52

Beats n n Temporal interference will occur when the interfering waves have slightly different frequencies Beating is the periodic variation in amplitude at a given point due to the superposition of two waves having slightly different frequencies 53

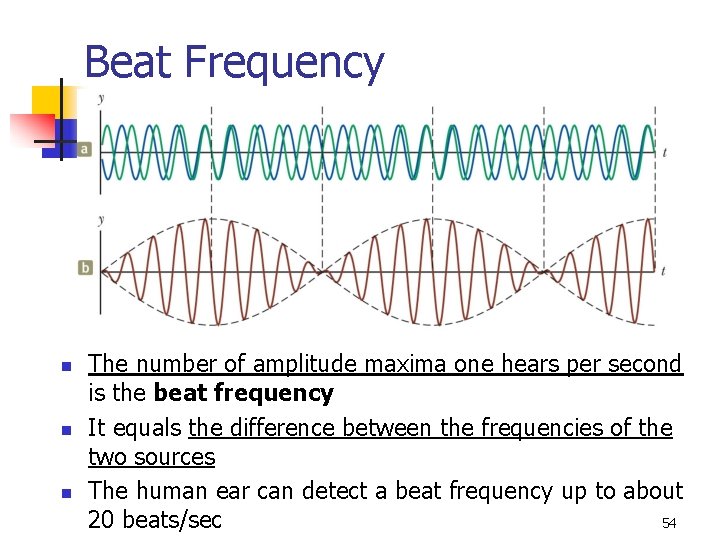
Beat Frequency n n n The number of amplitude maxima one hears per second is the beat frequency It equals the difference between the frequencies of the two sources The human ear can detect a beat frequency up to about 54 20 beats/sec

Beats, Final n The amplitude of the resultant wave varies in time according to n n Therefore, the intensity also varies in time The beat frequency is ƒbeat = |ƒ 1 – ƒ 2| 55

Nonsinusoidal Wave Patterns n n n The wave patterns produced by a musical instrument are the result of the superposition of various harmonics The human perceptive response associated with the various mixtures of harmonics is the quality or timbre of the sound The human perceptive response to a sound that allows one to place the sound on a scale of high to low is the pitch of the sound 56

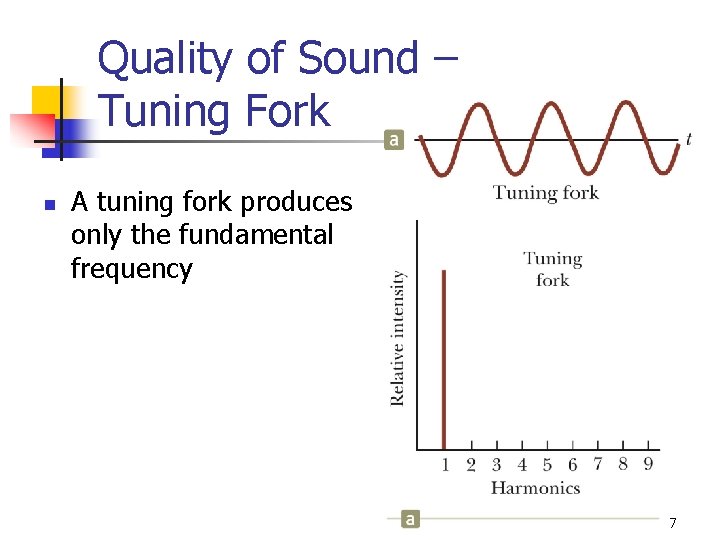
Quality of Sound – Tuning Fork n A tuning fork produces only the fundamental frequency 57

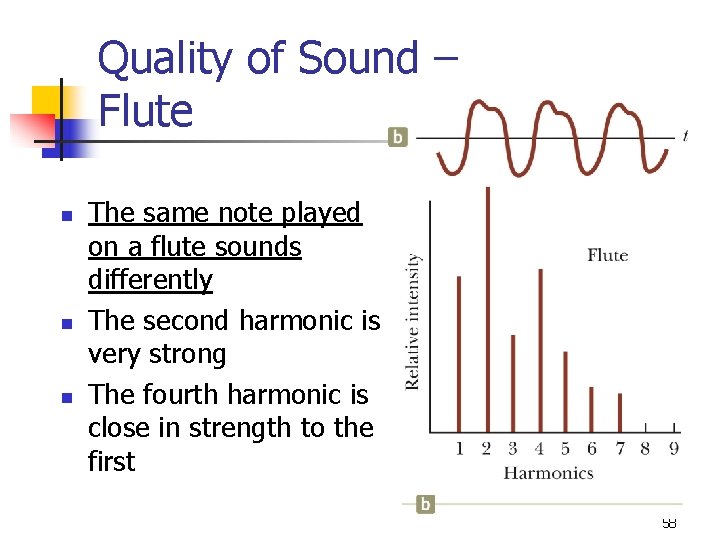
Quality of Sound – Flute n n n The same note played on a flute sounds differently The second harmonic is very strong The fourth harmonic is close in strength to the first 58

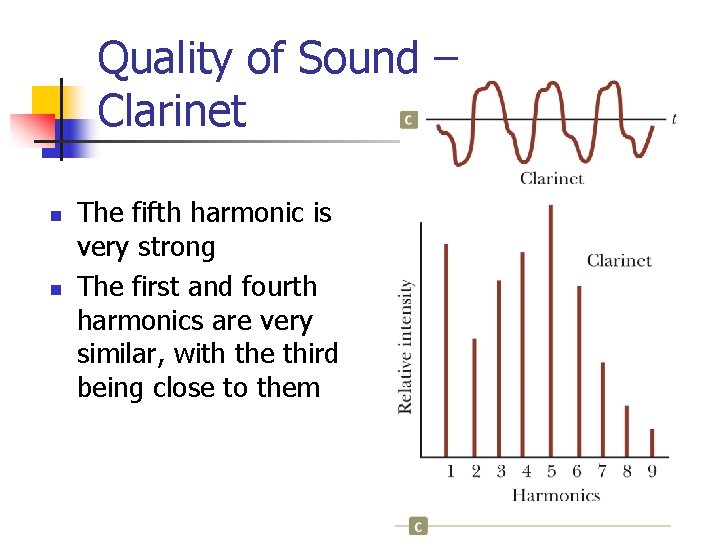
Quality of Sound – Clarinet n n The fifth harmonic is very strong The first and fourth harmonics are very similar, with the third being close to them 59

Analyzing Nonsinusoidal Wave Patterns n n If the wave pattern is periodic, it can be represented as closely as desired by the combination of a sufficiently large number of sinusoidal waves that form a harmonic series Any periodic function can be represented as a series of sine and cosine terms n This is based on a mathematical technique called Fourier’s theorem 60

Fourier Series n n A Fourier series is the corresponding sum of terms that represents the periodic wave pattern If we have a function y that is periodic in time, Fourier’s theorem says the function can be written as ƒ 1 = 1/T and ƒn= nƒ 1 An and Bn are amplitudes of the waves 61

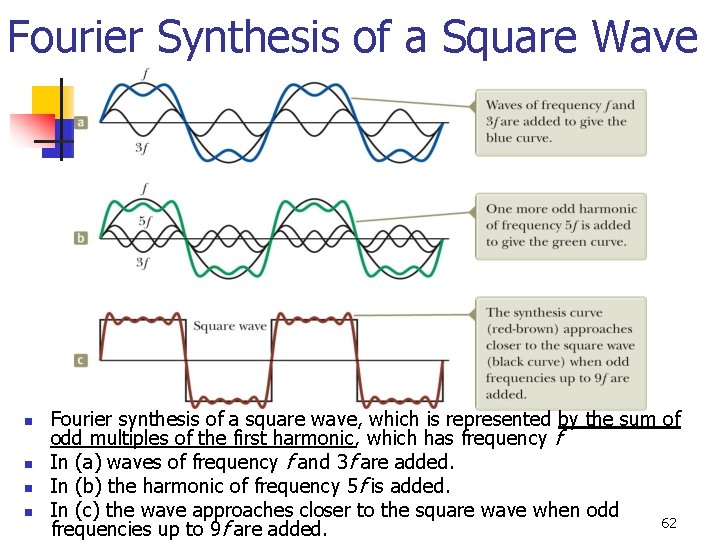
Fourier Synthesis of a Square Wave n n Fourier synthesis of a square wave, which is represented by the sum of odd multiples of the first harmonic, which has frequency f In (a) waves of frequency f and 3 f are added. In (b) the harmonic of frequency 5 f is added. In (c) the wave approaches closer to the square wave when odd 62 frequencies up to 9 f are added.
 Difference between standing crop and standing state
Difference between standing crop and standing state The principle of linear superposition
The principle of linear superposition Superposition
Superposition Superposition of waves
Superposition of waves Constructive interference of standing waves
Constructive interference of standing waves Standing wave
Standing wave Standing waves ch 12:1
Standing waves ch 12:1 Standing waves quiz
Standing waves quiz Standing waves
Standing waves Draw a picture of standing waves with n=3
Draw a picture of standing waves with n=3 Compare and contrast p waves and s waves using venn diagram
Compare and contrast p waves and s waves using venn diagram Difference between mechanical and electromagnetic waves
Difference between mechanical and electromagnetic waves Examples of mechanical waves
Examples of mechanical waves Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Long waves and short waves
Long waves and short waves Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Surface waves and body waves
Surface waves and body waves Mechanical waves and electromagnetic waves venn diagram
Mechanical waves and electromagnetic waves venn diagram Constructive
Constructive Principle of superposition in stress and strain
Principle of superposition in stress and strain Norton equation
Norton equation Difference between superposition and thevenin theorem
Difference between superposition and thevenin theorem Electromagnetic waves are longitudinal waves true or false
Electromagnetic waves are longitudinal waves true or false The wave chapter 13
The wave chapter 13 Is echolocation transverse or longitudinal
Is echolocation transverse or longitudinal Electromagnetic waves vs mechanical waves
Electromagnetic waves vs mechanical waves Is a seismic wave mechanical or electromagnetic
Is a seismic wave mechanical or electromagnetic What happens first intrusion or extrusion
What happens first intrusion or extrusion Superposition theorem examples
Superposition theorem examples Superposition fossils
Superposition fossils Superposition in fossils
Superposition in fossils Superposition of forces obey
Superposition of forces obey Mode superposition method
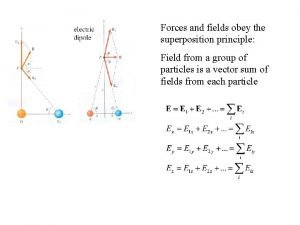
Mode superposition method Superposition principle electric field
Superposition principle electric field Principle of linear superposition
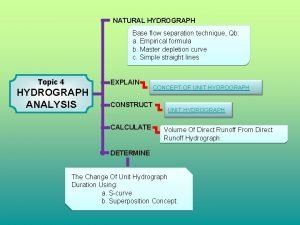
Principle of linear superposition Unit hydrograph superposition method
Unit hydrograph superposition method Superposition ece
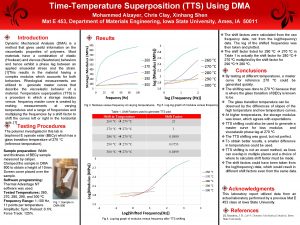
Superposition ece Time temperature superposition dma
Time temperature superposition dma Superposition of light
Superposition of light Principles of stratigraphy
Principles of stratigraphy Multism
Multism Principe de superposition exemple
Principe de superposition exemple Elec 202
Elec 202 Superposition theorem discussion
Superposition theorem discussion Malla circuito
Malla circuito Superposition
Superposition Entanglement vs superposition
Entanglement vs superposition Stratigraphic principles
Stratigraphic principles The threshold photoelectric effect in tungsten
The threshold photoelectric effect in tungsten Geologic history
Geologic history Rock layers and fossils worksheet
Rock layers and fossils worksheet Superposition oscillator
Superposition oscillator Superposition of matrices
Superposition of matrices Mechanical wave
Mechanical wave Chapter 14 vibrations and waves answers
Chapter 14 vibrations and waves answers Chapter 14 vibrations and waves
Chapter 14 vibrations and waves Chapter 17 mechanical waves and sound wordwise answer key
Chapter 17 mechanical waves and sound wordwise answer key Which travels along a surface separating two media
Which travels along a surface separating two media Chapter 17 mechanical waves and sound
Chapter 17 mechanical waves and sound Example of mechanical wave
Example of mechanical wave Chapter 14 vibrations and waves
Chapter 14 vibrations and waves Which travels along a surface separating two media
Which travels along a surface separating two media