Chapter 12 Gaussian Elimination II Speaker LungSheng Chien

Chapter 12 Gaussian Elimination (II) Speaker: Lung-Sheng Chien Reference book: David Kincaid, Numerical Analysis Reference lecture note: Wen-wei Lin, chapter 2, matrix computation http: //math. ntnu. edu. tw/~min/matrix_computation. html

Out. Line • Weakness of A=LU - erroneous judgment: A is invertible but A=LU does not exist - unstable, A is far from LU • • A=LU versus PA=LU Pivoting strategy Implementation of PA=LU MATLAB usage

Fail of LU: singular of leading principal minor Question: How about interchanging row 1 and row 2? and

unstable of LU: near singular of leading principal minor [1] ? Theoretical: , why? Numerical: Problem: for double-precision, we only have 16 digit-accuracy, we cannot accept if then

unstable of LU: near singular of leading principal minor [2] backward substitution step 1: step 2: Question: why not due to rounding error

unstable of LU: near singular of leading principal minor [3] Case 1: Case 2: wrong solution

unstable of LU: near singular of leading principal minor [4] Question: How about interchanging row 1 and row 2? LU-factorization backward substitution step 1: step 2: Key observation: without pivoting (rounding normal number) (rounding error does not occur for normal number)

unstable of LU: near singular of leading principal minor [5] Case 1: Case 2: Why not 1?

unstable of LU: cause and controllability define largest component of matrix without pivoting (stable) (NOT stable) Objective: control growth rate of control multiplier

Out. Line • Weakness of A=LU • A=LU versus PA=LU - controllability of lower triangle matrix L • Pivoting strategy • Implementation of PA=LU • MATLAB usage

Recall LU example in chapter 11 [1] 6 -2 2 4 1 12 -8 6 10 2 3 -13 9 3 0. 5 -6 4 1 -18 -1 since 1 1 1 -2 2 4 0 -4 2 2 0 -12 8 1 0 2 3 -14 is not maximum among 6 -2 2 4 0 -4 2 2 1 0 -12 8 1 3 0 2 3 -14 -0. 5 since 6 1 1 1 is not maximum among 6 -2 2 4 0 -4 2 2 0 0 2 -5 0 0 4 -13

Recall LU example in chapter 11 [2] 1 6 -2 2 4 0 -4 2 2 0 0 2 -5 1 0 0 4 -13 2 since 1 -2 2 4 0 -4 2 2 0 0 2 -5 0 0 0 -3 is not maximum among 6 -2 2 4 1 12 -8 6 10 2 1 3 -13 9 3 0. 5 3 1 -6 4 1 -18 -1 -0. 5 2 Question: How can we control 1 6 6 -2 2 4 -4 2 2 2 -5 1 , is uniform bound possible? -3

PA = LU in MATLAB

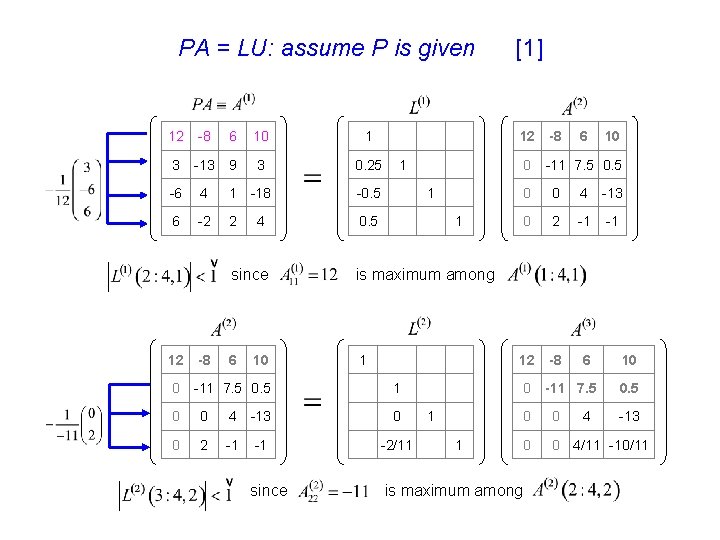
PA = LU: assume P is given 12 -8 6 10 1 3 -13 9 3 0. 25 -6 4 1 -18 -0. 5 6 -2 2 4 0. 5 1 0 -11 7. 5 0. 5 1 0 0 4 -13 0 0 2 -1 -1 -2/11 since 0 -11 7. 5 0. 5 1 1 6 10 0 0 4 -13 0 2 -1 -1 12 -8 6 0 -11 7. 5 1 6 10 -8 1 is maximum among -8 12 1 since 12 [1] 0. 5 0 0 4/11 -10/11 is maximum among 4 10 -13

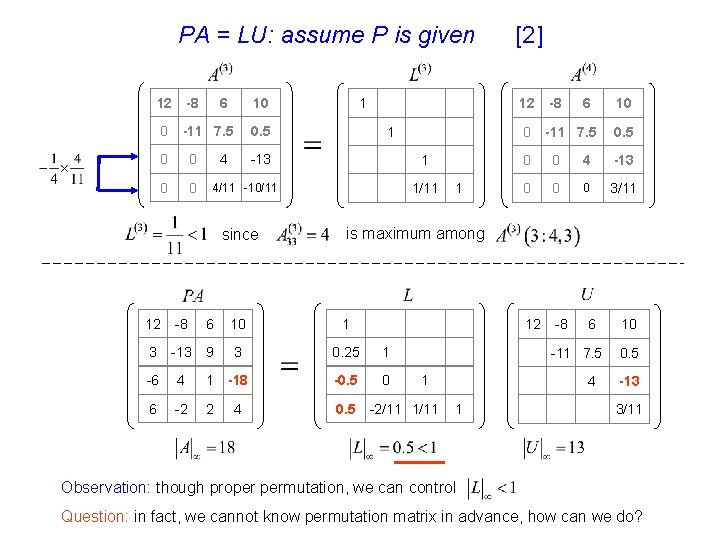
PA = LU: assume P is given 12 -8 0 -11 7. 5 0 0 6 10 1 0. 5 4 1 -13 1 1/11 4/11 -10/11 since 1 [2] 12 -8 6 0 -11 7. 5 10 0. 5 0 0 4 -13 0 0 0 3/11 12 -8 is maximum among 12 -8 6 10 1 3 -13 9 3 0. 25 1 -6 4 1 -18 -0. 5 0 6 -2 2 4 0. 5 6 -11 7. 5 1 -2/11 1/11 4 1 10 0. 5 -13 3/11 Observation: though proper permutation, we can control Question: in fact, we cannot know permutation matrix in advance, how can we do?

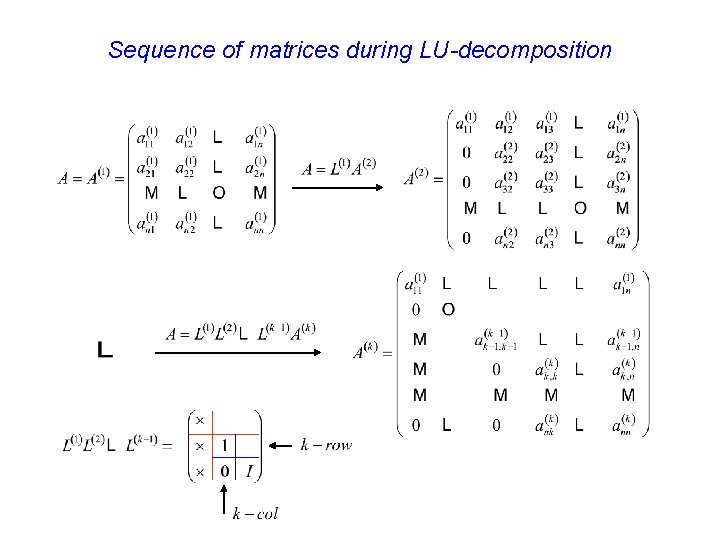
Sequence of matrices during LU-decomposition

Out. Line • Weakness of A=LU • A=LU versus PA=LU • Pivoting strategy - partial pivoting (we adopt this formulation) - complete pivoting • Implementation of PA=LU • MATLAB usage

Partial pivoting and complete pivoting Partial pivoting such that (1) find a (2) swap row then and row with complete pivoting such that (1) find a (2) swap row and row (2) swap column then and column with

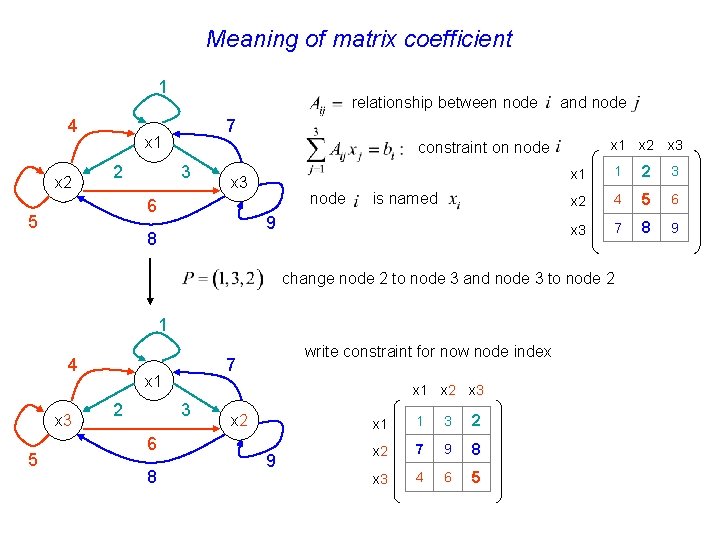
Recall permutation matrix Let Define permutation matrix interchange row 2, 3 interchange column 2, 3 Symmetric permutation: 1 2 3 4 5 6 7 8 9 1 2 3 interchange 7 8 9 row 2, 3 4 5 6 1 3 2 interchange 7 9 8 column 2, 3 4 6 5

Meaning of matrix coefficient 1 4 x 2 relationship between node 7 x 1 2 x 1 x 2 x 3 constraint on node 3 x 3 6 5 and node is named 9 8 x 1 1 2 3 x 2 4 5 6 x 3 7 8 9 change node 2 to node 3 and node 3 to node 2 1 4 x 3 5 x 1 2 x 1 x 2 x 3 3 6 8 write constraint for now node index 7 x 2 9 x 1 1 3 2 x 2 7 9 8 x 3 4 6 5

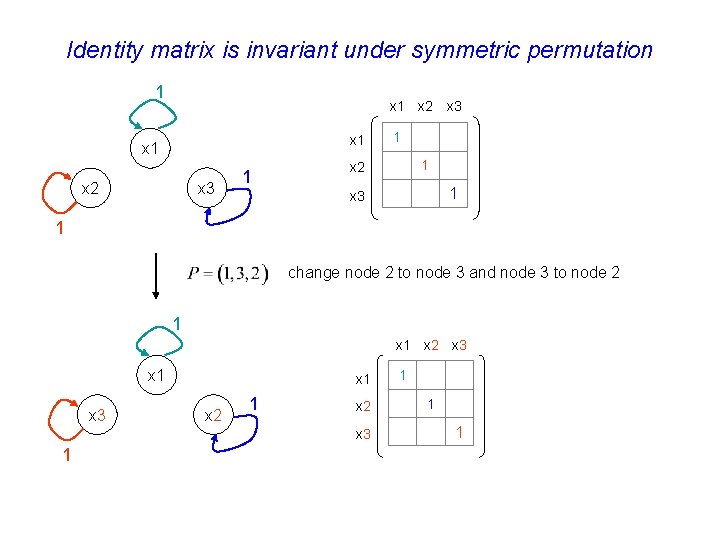
Identity matrix is invariant under symmetric permutation 1 x 2 x 3 x 1 x 3 x 2 1 1 1 x 2 1 x 3 1 change node 2 to node 3 and node 3 to node 2 1 x 2 x 3 x 1 x 2 x 3 1 1

PA = LU: partial pivoting [1] 6 -2 2 4 12 -8 6 10 6 -2 2 4 3 -13 9 3 -6 4 1 -18 12 -8 6 10 0 2 -1 -1 12 -8 6 10 1 6 -2 2 4 0. 5 3 -13 9 3 0. 25 -6 4 1 -18 -0. 5 1 1 0 1 -11 7. 5 0 0 4 6 10 12 -8 0 2 -1 -1 0 -11 7. 5 0 2 -1 -1 0 0 4 -13 0 0 0 4 -13

PA = LU: partial pivoting [2] where 1 0. 5 0. 25 1 1 1 0. 5 1 -0. 5 1 verify Interchange columns 2, 3 0. 25 1 1 -0. 5 12 -8 6 10 1 3 -13 9 3 0. 25 6 -2 2 4 0. 5 -6 4 1 -18 -0. 5 Interchange rows 2, 3 1 1 1 -0. 5 6 1 12 -8 10 0 -11 7. 5 0 2 -1 -1 0 0 4 -13

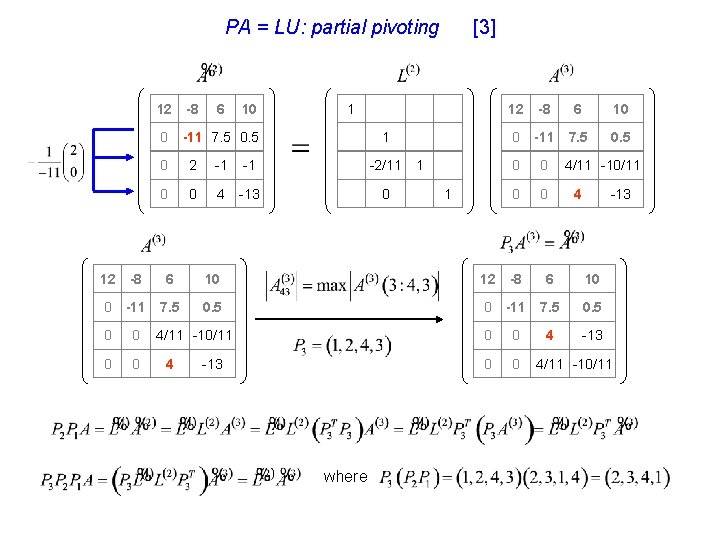
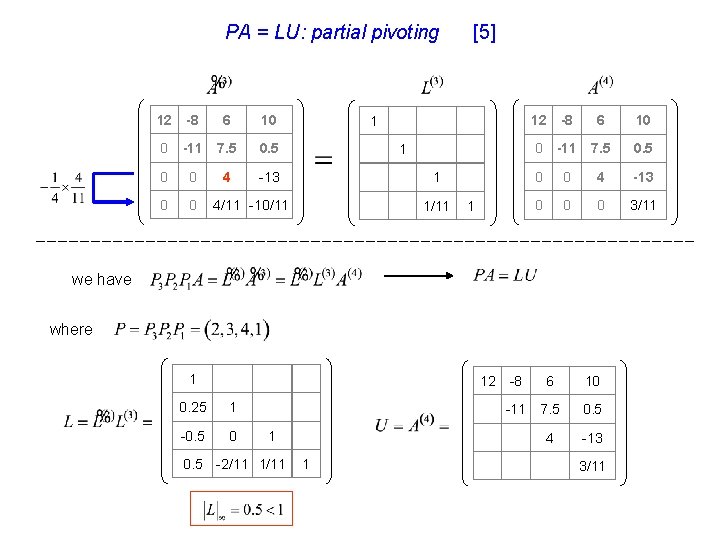
PA = LU: partial pivoting 12 -8 6 10 0 -11 7. 5 0. 5 [3] 1 1 0 2 -1 -1 -2/11 0 0 4 -13 0 1 1 12 -8 6 10 0 -11 7. 5 0 0 0 0 4/11 -10/11 4 -13 12 -8 6 10 0 -11 7. 5 0 0 4 -13 0 0 4/11 -10/11 4 -13 where 4/11 -10/11

PA = LU: partial pivoting 1 0. 25 0. 5 [4] 1 1 1 Interchange columns 3, 4 -2/11 1 -0. 5 1 verify 0. 25 1 0. 5 -2/11 -0. 5 0 1 Interchange rows 3. 4 1 12 -8 6 10 1 3 -13 9 3 0. 25 1 -6 4 1 -18 -0. 5 0 6 -2 2 4 0. 5 -2/11 1 1 0. 25 1 -0. 5 0 0. 5 -2/11 12 -8 6 10 0 -11 7. 5 0 0 4 -13 0 0 4/11 -10/11 1 1

PA = LU: partial pivoting 12 -8 6 10 0 -11 7. 5 0 0 4 -13 0 0 [5] 1 1 1 4/11 -10/11 1 12 -8 6 10 0 -11 7. 5 0 0 4 -13 0 0 0 3/11 we have where 1 12 0. 25 1 -0. 5 0 0. 5 1 -2/11 1 -8 6 10 -11 7. 5 0. 5 4 -13 3/11

Out. Line • • Weakness of A=LU versus PA=LU Pivoting strategy Implementation of PA=LU - commutability of GE matrix and permutation - recursive formula • MATLAB usage

Implementation issue: commutability of GE matrix and permutation [1] 1 1 0. 5 0. 25 1 0. 25 Interchange rows and columns 2, 3 1 -0. 5 1 -0. 5 1 1 0. 25 1 1 Interchange rows and columns 3, 4 -2/11 1 1 0. 25 1 -0. 5 0 0. 5 -2/11 1 1

Implementation issue: commutability of GE matrix and permutation [2] Observation: If we define , then where interchanges rows and interchange or columns

Implementation issue: commutability of GE matrix and permutation [3] partial rows (k and p) interchange symmetric permutation on an Identity matrix

Algorithm ( PA = LU ) Given full matrix use permutation vector let , [1] , construct initial lower triangle matrix to record permutation matrix and for we have compute update original matrix stores in lower triangle matrix

Algorithm ( PA = LU ) 1 find a such that 2 swap row and row [2] define permutation matrix , we have then after swapping rows compute 3 if 4 for then compute then endif by swapping and

Algorithm ( PA = LU ) 5 decompose [3] where by updating matrix then endfor (recursion is done)

Question: recursion implementation normal abnormal Extension of algorithm • Initialization - check algorithm holds for k=1 • Recursion formula - check algorithm holds for k, if k-1 is true • Termination condition - check algorithm holds for k=n • Breakdown of algorithm - check which condition PA=LU fails • Exception: algorithm works only for square matrix?

Exception: algorithm works only for square matrix? Case 1: Case 2: [1]

Exception: algorithm works only for square matrix? Case 3: we can simplify it as Question: what is termination condition of case 3 ? [2]

Out. Line • • • Weakness of A=LU versus PA=LU Pivoting strategy Implementation of PA=LU MATLAB usage - abs - max

Command “abs”: take absolute value In PA=LU algorithm, we need to take absolute value of one column vector for pivoting abs also works for matrix

Command “max”: take maximum value