CHAPITRE 10 Equations diffrentielles Equations diffrentielles ordre 1

CHAPITRE 10 Equations différentielles

Equations différentielles ordre 1 F ( t , y(t) , y’(t)) = 0 , t e I Temps vitesse position F ( t , y(t) , y’’ (t)) = 0 , t e I ordre 2 accélération

Equations linéaires d’ordre 1 y’ (t) = a(t) y(t) + b(t) , t e I (a et b fonctions continues de I dans R ou C) + Condition « initiale » : y(t 0) = y 0 (t 0 e I , y 0 e R ou C)

L’approche numérique : méthode d’Euler • Se fixer des conditions initiales t 0, y 0 • Choisir un pas de temps t • Choisir T = « durée de vie » tel que [t 0, T] soit inclus dans I ut, 0 = y 0 approximation de y(t 0 + nt) ut, n+1 = ut, n + t ( a(t 0 + nt) ut, n + b(t 0+nt)) (tant que t 0 + nt b T)

Le théorème de Cauchy Hypothèses : - I intervalle ouvert de R - a et b fonctions continues de I dans R (ou C) - t 0 e I y 0 e R ou C (données initiales) Conclusion : Il existe unique courbe intégrale de Il existe unique fonction l’équation différentielle y : I R (ou C) telle que : y’(t)= a(t) y(t) + b(t) y’ (t)= a(t) y(t) + b(t) pour t dans I y(t passant par le point (t 0) = y 0 (condition initiale) 0, y 0)

L’attaque du problème : étape 1 : résolution de l’équation homogène Y’ = 0 y ’ (t) = a(t) y(t) + b (t)Y = constante t A (t) = ! a(t) dt t 0 fonction auxiliaire : Y(t) = y(t) exp (-A (t)) 1 degré de liberté y (t) = C exp (A (t))

L’attaque du problème : étape 2 : recherche d’une solution particulière de l’équation complète y ’ (t) = a(t) y(t) + b (t) variation de la constante y (t) = C(t) exp (A (t)) (C’(t) + a(t) C(t)) exp(A(t)) = a(t) C(t) exp (A(t)) + b(t) t (-A (t)) C’ (t) = b(t) exp ! y part (t) = exp(A(t)) C(t) = C + t 0 b(u) exp (-A(u))

Le bilan final Solutions de l’équation y’(t)=a(t) y(t)+ b(t) : avec condition initiale : y(t 0) = y 0 ( t ! y(t) = exp(A(t)) z C 0 + t 0 ) b(u) exp(-A(u)) du z 0=y 0 exp(-A(t 0))=y 0 Condition initiale : y(t 0) = y 0

Les équations de J. Bernouilli a y’(t) = a(t) y(t) + b(t) [y(t)] z’(t) = (1 -a) a(t) z(t) + (1 -a) b(t) (a e R {0, 1}) 1 -a Condition initiale : y(t z(t 00) = y 00 > 0 Fonction auxiliaire : z(t) = [y(t)] 1 -a

Equations linéaires d’ordre 2 y’’ (t) = a(t) y’(t) + b(t) y(t) + c(t) , t e I (a, b, c fonctions continues de I dans R ou C) + Conditions « initiales » : y(t 0) = y 0 y’(t 0)=v 0 (t 0 e I , y 0 , v 0 e R ou C)

Un exemple de motivation : une cellule electronique d’ordre 2 i (UA – UC ) (t) = R i(t) + L di/dt c (U C-UD)’ (t) = i (t) y(t) = Uc –UD (t) f(t) = UA –UB (t) Lc y’’ (t) + R c y’(t) + y(t) = f(t)

L’approche numérique : méthode d’Euler • Se fixer des conditions initiales t 0 , y 0 , v 0 • Choisir un pas de temps t approximation de y(t 0 + nt) • Choisir T = « durée de vie » tel que [t 0, T] soit inclus dans I ut, 0 = y 0 , ut, 1=y 0 + t v 0 ut, n+2 = ut, n (t 2 b(t 0+nt) –t a(t 0+nt)-1) + ut, n+1 ( t a(t 0 + nt) + 2) + t 2 c(t 0+nt)

Le théorème de Cauchy Hypothèses : - I intervalle ouvert de R - a , b , c fonctions continues de I dans R (ou C) - t 0 e I y 0 , v 0 e R ou C (données initiales) Conclusion : Il existe unique fonction Il existe unique courbe intégrale de l’équation différentielle y : I R (ou C) telle que : y’’(t)= a(t) y’(t) + b(t) y(t) + c(t) y’’ (t)= a(t) y’(t) + b(t) y(t) + c(t) pour t dans I y(t 0) = y 0 , y’(t 0)=v 0 (conditions initiales) passant par le point (t 0, y 0) et ayant au point (t 0, y 0) une tangente de pente v 0

Le cas « à coefficients constants » Hypothèses : - I intervalle ouvert de R - a , b e R ou C , c fonction continue de I dans R (ou C) - t 0 e I y 0 , v 0 e R ou C (données initiales) Conclusion : Il existe unique fonction Il existe unique courbe intégrale de l’équation différentielle y : I R (ou C) telle que : y’’(t)= a y’(t) + b y(t) + c(t) y’’ (t)= a y’(t) + b y(t) + c(t) pour t dans I y(t 0) = y 0 , y’(t 0)=v 0 (conditions initiales) passant par le point (t 0, y 0) et ayant au point (t 0, y 0) une tangente de pente v 0

L’attaque du problème : étape 1 : résolution de l’équation homogène y’’(t) – a y’ (t) – b y(t) = 0 , t e R a , b e C ? y(t) = exp ( w t) solution ? w 2 – a w – b = 0 X 2 – a X – b = 0 (équation caractéristique) = (X- w 1) (X-w 2) cas 1 : a 2 + 4 b non nul w 1 et w 2 distinctes y = C 1 exp(w 1 t) + C 2 exp (w 2 t) OK cas 2 : a 2 + 4 b = 0 w 1= w 2 =w y = C 1 exp(w t) + C 2 t exp (w t) OK

L’attaque du problème : résolution de l’équation homogène (cas complexe (2)) a , b complexes + conditions initiales (y 0 , v 0 e C) cas 1 : a 2 + 4 b non nul w 1 et w 2 distinctes cas 2 : a 2 + 4 b = 0 w 1= w 2 =w y = C 1 exp y 1(t) (w 1 t) + C 2 exp y 2(t) (w 2 t) OK y = C 1 exp (w t) + C 2 t yexp (w t) OK y 1(t) 2(t) C 1 y 1(t 0) + C 2 y 2(t 0) = y 0 C 1 y’ 1(t 0) + C 2 y’ 2(t 0) = v 0 solution (C 1, C 2) système de Cramer ! unique !!

l= a/2 <0 : oscillations amorties l= a/2 >0 : oscillations amplifiées L’attaque du problème : l’équation homogène dans le cas réel (1) y’’(t) – a y’ (t) – b y(t) = 0 , t e R a , b e R X 2 – a X – b = 0 (équation caractéristique) = (X- l 1) (X-l 2) cas 1 : a 2 + 4 b > 0 inf(lj)>0 : « explosion » l 1 et l 2 réels distincts y = C 1 exp(l 1 t) + C 2 exp (l 2 t) OK cas 2 : a 2 + 4 b = 0 sup(lj)<0 : « extinction » l>0 : « explosion » l racine réelle double y = C 1 exp(l t) + C 2 t exp (l t) OK cas 3 : a 2 + 4 b < 0 racines l +/- i w l<0 : « extinction » y = exp(l t) (C 1 cos(wt) + C 2 sin (w t)) OK

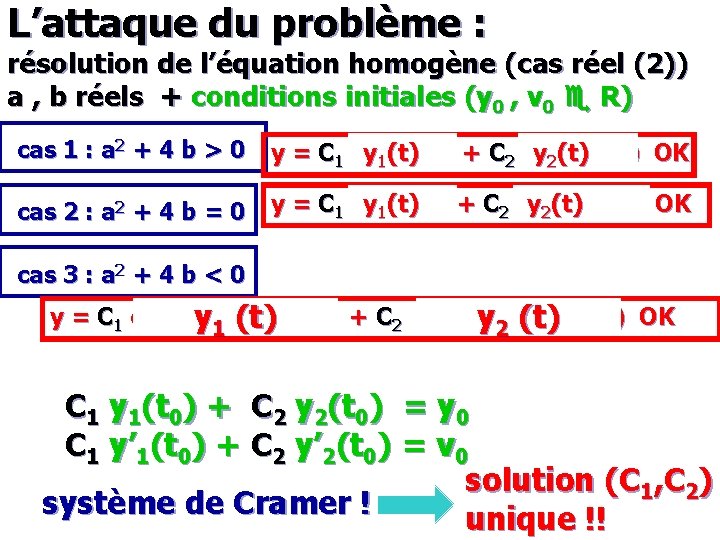
L’attaque du problème : résolution de l’équation homogène (cas réel (2)) a , b réels + conditions initiales (y 0 , v 0 e R) cas 1 : a 2 + 4 b > 0 y = C 1 exp (l 1 t) + C 2 exp (l 2 t) OK y 1(t) y 2(t) cas 2 : a 2 + 4 b = 0 y = C 1 exp (l t) + C 2 t y 1(t) yexp 2(t) (l t) OK cas 3 : a 2 + 4 b < 0 y = C 1 exp(ly t) cos ( w t) + C 2 exp (y l 2 t) sin ( (t) w t) OK 1 (t) C 1 y 1(t 0) + C 2 y 2(t 0) = y 0 C 1 y’ 1(t 0) + C 2 y’ 2(t 0) = v 0 solution (C 1, C 2) système de Cramer ! unique !!

Recherche d’une solution particulière de l’équation « avec second membre » ! ! { t y 2 (u) c(u) du C (t) I. Méthode de « variation des constantes C 11’(u) = - --------- (y 1 y 2’ – y 2 y 1’)(u) y’’(t)=a y’(t) + b y(t) + c(t) t 0 t y OK dès que : système de Cramer ! 1 (u) c (u) C (t) du C 22’(u) = --------- (y y 1’)(u) C’ 1 y 11 y + C’ 22 y 2’ – y 2 = 0 1 1 2 2 t 01 y’ 1 + C’ 2 y’ 2 = c C’ Solution unique (C 1’, C 2’) ypart (t) C 1(t) y(t) = C y 2(t) C 2(t) 1 y 1(t) + C

Bilan : la solution du problème de Cauchy (cond. initiales : y 0, v 0) solution générale de l’équation y’’(t) – a y’(t) – by(t)=0 t ! y (t) = C 1 y 1(t) + C 2 y 2 (t) + c(u) (y 1(u) y 2 (t) – y 2 (u) y 1 (t)) ------------------ du y 1(u) y 2’(u) – y 2(u)y 1’(u) t 0 C 1 y 1(t 0) + C 2 y 2 (t 0) = y 0 C 1 y 1’(t 0) + C 2 y 2’(t 0) = v 0 solution particulière de l’équation y’’ (t) – a y’(t) – b y(t) = c(t)

Remarque II. Une autre méthode pour la recherche d’une solution particulière de y’’(t) – a y’(t) – by(t) = c(t) Si le second membre c est de la forme : P(t) exp(w t) , w e C P(t) cos (wt) , w e R P(t) sin (wt) , w e R On cherche une solution particulière de la forme : ypart(t) = Q (t) exp (wt), deg (Q) b deg (P) +2 (par exemple par identification)

Fin du chapitre 10